A Proof System Based on Ramsey Theory
Possible quasi-polynomial size proofs for tautologies based on Ramsey theory

Endre Szemerédi is one of the greatest combinatorists in the world. He is famous, of course, for solving the Erdös-Turán arithmetic progression conjecture, proving the powerful regularity lemma, and for a many other terrific results. He has won many prizes, including the Pólya prize, Steele Prize, and the Schock Prize.
Today I plan to talk about a potential relationship between combinatorial theorems and proof systems for tautologies. As you know I am not afraid, to appear foolish, while suggesting approaches to problems that most think are false. In this post, it is an approach to obtain quasi-polynomial sized proofs for tautologies. I thought for a while that this could potentially succeed, but now I am less confident that it is on the right track. However, I would like to share it with you, and let you decide for yourself.
Since Szemerédi plays a role in my proposed proof system, I thought I would say something about him first. Years ago I looked at Szemerédi’s paper that proves his famous arithmetic progression theorem. I do not claim to have understood the proof, but I wanted to see the masterpiece for myself.
An aside: I think we all can benefit from at least looking at some the great masterpieces. While the details may not be easy to follow, especially for a non-expert, looking at these papers is an experience that is valuable. Take a look at Walter Feit and John Thompson’s paper, Andrew Wiles’s paper, Ben Green and Terence Tao’s paper, the proof of the PCP theorem, and so on. Really.
Endre’s paper was so complex that I recall it has a figure that is a flow-chart, which shows the dependencies of the various parts of the proof. However, the coolest part of the paper is–in my opinion– in the acknowledgment, where Szemerédi said:
“I would like to thank Ron Graham for writing the paper.”
Amazing. It was all Endre’s work, but Ron wrote the paper.
When I was at Princeton working with Dan Boneh, we once needed a constructive version of Andy Yao’s XOR lemma. At the time the proofs of this lemma were not strong enough for our application. So for a COLT paper we proved what we needed from scratch–luckily we only needed a special case, so the proof was not too difficult.
However, Dan and I still wanted to be able to prove the full case, and after getting nowhere we asked Szemerédi for help. He was kind enough to come down from Rutgers and visit me at my Princeton office to discuss the problem. After a while, he understood the problem and said to me that either he could solve it in the next day or two or the problem was hopeless.
Two days later I got a phone call from Endre, who said that he had proved what we wanted. I was thrilled and immediately responded that I would be happy to come up to Rutgers to hear the details. Endre said no, that would not be necessary, since the proof was “so easy.” In the next few minutes he spoke fast and outlined a proof using an entropy type argument. I furiously wrote down all I could follow. Then, he said good-bye.
I remember running down to Dan’s office and excitedly telling him we had the solution. The trouble was that my notes were meager and we were not Endre. But, in a mere three hours or so, we re-constructed his argument. As I recall, Dan and I wrote up a draft of the result with all three as authors, but we never tried to publish it. Does that make our Szemerédi number ?
Ramsey Theory and PCP
The famous Ramsey theorem will play an important role in the suggested proof system. For a graph let as usual
be the size of the largest clique of
. Also define
, if in every
coloring of the edges of
, there is a set of vertices
of size at least
, so that
forms a clique of
and all the edges in
are the same color. The famous Ramsey theorem states that for
fixed,
tends to infinity as
tends to infinity.
There are other Ramsey style theorems that are also needed. The following is a generalization of the above to “hypergraphs.” These concern coloring of not edges, but coloring of -cliques of the graph. Define
, if in every
coloring of the
-cliques of
, there is a set of vertices
of size at least
, so that
forms a clique of
, and all
-subsets of
have the same color. Also for fixed
and
,
tends to infinity as
tends to infinity.
Another important ingredient, for our approach is the PCP gap theorem for cliques. One of the best bounds is due to David Zuckerman:
Theorem: It is NP-hard to approximate the max-clique problem to within a factor of

Actually, under stronger assumptions can tend to
slowly.
A Proof System
Suppose that is a graph that either has only small cliques all of size at most
, or has at least one large clique of size
. We do not know how in polynomial time to determine whether or not a graph is in either of these categories: small or large. The goal here is to present a simple proof system based on Ramsey theory that might be able to supply a quasi-polynomial size proof that
does not have a large clique.
This is the proof system:
- Let
where
;
- Guess a
-coloring of the edges of
;
- For each set of
vertices of
, check if they form a mono-chromatic clique of
;
- If all fail to be mono-chromatic, then state that
has no large clique.
There are several issues with this “proof system.” Let’s skip the discussion of step (1), and return to that later on. The size of the proof is dominated by the cost of step (3): this takes at most quasi-polynomial time, since
is at most order
. Next the proof system is sound: if it states that
has no large clique, then this is true. Note, if
has a large clique, then just that part of the graph will always have a mono-chromatic clique of size at least
. So the system is sound.
The central question is simple: is the proof system complete? The only way that it could fail to be complete is if there were a graph
so that
, and yet for all
-colorings, there is a mono-chromatic clique of size
. If there is no such graph, then the proof system is complete. Thus, a key question, that I do not know the answer to, is: Do such graphs exist?
There is one loose end. In step (1) we need the value
? The way we fix this is to allow the proof system
bits of advice. This follows since it is well known that
is always at most logarithmic in the size of the graph.
Another Proof System
We can also extend the proof system via hypergraph Ramsey theory. Again suppose that
is a graph that either has only small cliques all of size at most
, or has at least one large clique of size
.
This is the second proof system:
- Let
where
;
- Guess a
-coloring of the
-cliques of
;
- For each set
of
vertices of
, check that
is a clique of
, so that all the
subsets of
are labeled with the same color.
- If all fail this test, then state that
has no large clique.
As before, step (1) will be done through advice bits. The size of the proof is dominated by the cost of step (3): this takes at most quasi-polynomial time, since
and
are at most order
. Next the proof system is sound: if it states that
has no large clique, then this is true. Note, if
has a large clique, then just that part of the graph will always have a mono-chromatic clique of size at least
. So the system is sound.
Again completeness is the open problem, and the role of Szemerédi was as an informal oracle. I ran similar ideas by him, years ago, and he seemed to think that it was not obvious whether or not the proof systems worked. Any mistake is mine, but I thought that his comments were at least comforting.
The reason for the second system is that the first might be incomplete, while the second is complete. The advantage of the second system is our lack of knowledge of the behavior of hypergraph Ramsey numbers. In a funny way, the fact that these numbers are so poorly understood, means that the second proof system might be harder to show incomplete. It might even be complete.
Open Problems
Of course the obvious question is to show that these proof systems are incomplete, especially if you believe that tautologies are hard. Or try to show that one of them is complete. Note, the second proof system is really a family of systems, since we are free to select
and
.
Another possibility is to create other similar proof systems, perhaps based on other Ramsey type theorems. Other examples, would, in my opinion, be quite interesting.
I think using the PCP theorem as part of a proof system seems to be a powerful idea. Again, while the proof system outlined is likely not to be complete, its incompleteness would shed light on Ramsey theory itself. That would be another example of Reverse Complexity Theory.
Lastly, can oracle results shed any light here? Can the known oracle results show that this type of proof systems cannot work? You know how I feel about oracle results, but can they say something here?
16 Comments leave one →Trackbacks
Leave a Reply
- Let


Is it true that if we assume a strengthened exponential time hypothesis then there would be no such proof sytem? The strengthened ETH I’m talking about is that 3SAT is not in co-QNP, i.e. co-3SAT does not have witnesses of quasipolynomial size?
Because in my eyes that’s a pretty good evidence against the existence of such proof systems.
Elad,
Why is that evidence? P could equal NP.
Hi Dick, Can you please add a search widget on your blog ? It makes searching for older posts easier. Thanks.
I very much enjoy your contrarian thinking, but I’m pretty sure that the problem you ask has the answer that you don’t want, and that a random graph with appropriate edge probability would be a counterexample. For instance, it is known that you can choose the edge probability in such a way that you have no complete subgraph of order , and yet for any 2-colouring of the vertices you get a monochromatic
, and yet for any 2-colouring of the vertices you get a monochromatic  .
.
But that is for fixed , so it is probably not possible to read off from the proof (which is due, if I remember correctly, to Rodl and Rucinski) the result you are asking for, or rather asking not to be true. This is an area I have been thinking about a lot recently, because David Conlon and I came up with a new and very general proof method for this kind of theorem. Without thinking about it quite a bit harder, I can’t say whether there is any chance that we could get from fixed
, so it is probably not possible to read off from the proof (which is due, if I remember correctly, to Rodl and Rucinski) the result you are asking for, or rather asking not to be true. This is an area I have been thinking about a lot recently, because David Conlon and I came up with a new and very general proof method for this kind of theorem. Without thinking about it quite a bit harder, I can’t say whether there is any chance that we could get from fixed  to something that’s almost as big as the Ramsey bound for the complete graph, but it doesn’t seem completely obviously out of the question. At any rate, I would conjecture that if you randomly remove just enough edges from the complete graph to get rid of all cliques of size
to something that’s almost as big as the Ramsey bound for the complete graph, but it doesn’t seem completely obviously out of the question. At any rate, I would conjecture that if you randomly remove just enough edges from the complete graph to get rid of all cliques of size 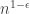 , then in any 2-colouring of that graph you will get monochromatic cliques of size
, then in any 2-colouring of that graph you will get monochromatic cliques of size  , where
, where  is as you defined it.
is as you defined it.
Thanks for the comment. I should have said that random or near random is my guess too as the best “bad” graph. The rub I hoped was getting the graph to exactly have the right properties could be delicate.
Of course, the other side of coin here is that if you do believe that there is proof system possible–as an axiom–then it is immediate that such graphs exist. So suppose you can prove by a non-trivial argument that they exist. Then, complexity theory yields the same result, but with a much simpler proof.
Also what about the higher Ramsey issues. I included them because I thought it might be technically more challenging to create such “bad” graphs.
Did you mean that the *impossibility* of a good proof system for tautology immediately implies that such graphs exist?
I agree that getting the results exactly right looks delicate, but that feels more like a technical problem than a reason to believe that no such graph exists. I’d say something similar about the hypergraph generalization, though at least for configurations of bounded size the method I have with David Conlon is not substantially more difficult for hypergraphs than it is for graphs.
But however all that turns out, you’ve raised an interesting question that I hadn’t thought of — trying to find such a graph looks as though it could be a very good test of what we can and can’t say about configurations in subsets of random sets. I’ll let you know if I come up with anything more precise to say. (For instance, perhaps a first result would be to obtain a graph with no clique of size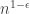 such that for any 2-colouring you could always find a monochromatic
such that for any 2-colouring you could always find a monochromatic 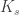 , where
, where  was pretty close to the best possible
was pretty close to the best possible  but not quite equal to it. Even that seems to be quite a nice problem.)
but not quite equal to it. Even that seems to be quite a nice problem.)
At the end of the post you ask whether oracle results might give counterexamples. Probably not, but for questions of this kind one can often get counterexamples from circuit lower bounds.
If your proof system worked, then you would have a “non-deterministic bounded depth circuit of size n^O(log n)” for the problem of distinguishing graphs with clique size more than n^{1-eps} from graphs with clique size less than n^eps.
I don’t think there are known lower bounds for *non-deterministic* bounded-depth circuits, but at some point I convinced myself (but never wrote up rigorously) that from Braverman’s resolution of the Linial-Nisan conjecture and some extra work one can prove that sub-exponential size bounded-depth deterministic circuits cannot distinguish clique size less than n^eps from clique size more than n^{1-eps}. (This is helpful in ruling out various “PCP + brute force” algorithmic approaches, although not your specific proposal.)
Luca,
This is a wonderful idea. Never thought about the fact that these are constant depth. Would be great if it worked out. Great insight. This would be truly a neat example of RCT: reverse complexity theory.
On second thought, this wouldn’t work for your proof system (or for candidate *proof systems* in general, as opposed to candidate *algorithms*) because if NP=coNP then every problem in coNP has a polynomial size bounded-depth non-deterministic circuit (the reduction from a generic problem in NP to SAT can be done in NC0, and the validity of a SAT witness can be checked in AC0), so one cannot hope to prove unconditional lower bounds for bounded depth non-deterministic circuits.
Heh, the original paper about the Grothendieck-Riemann-Roch theorem was famously written by Serre and Dieudonne (if I remember properly), because Grothendieck didn’t like his own proof so didn’t write it up. Serre and Dieudonne put their own names on the paper but they of course explained in it that it was Grothendieck’s work and that their contribution was purely editorial.
Correcting my own post, the authors of that paper were JP Serre and Armand Borel:
http://www.numdam.org/item?id=BSMF_1958__86__97_0
It says it consists of notes from a seminar held at Princeton in 1957 about the work of Grothendieck and the new results in it are his, etc.
I don’t know exactly which paper you are referring, but I checked Szemeredi’s Acta Arithmetica paper and in the acknowledgment found the names RL Graham and A Hajnal. Anyway it’s very funny.
http://matwbn.icm.edu.pl/ksiazki/aa/aa27/aa27132.pdf
Thanks for a great post as usual. This is one of the best technical blogs I know of.
Here is the the exact statement, I apologize I forgot to cite Hajnal too: “In fact, they wrote the whole paper after listening to my rough oral exposition.”