What If Cantor’s Proof Is Wrong?
Believing impossible things
The Red Queen—I do not know her full name—is one of the most colorful characters in Lewis Carroll’s Through the Looking-Glass. She is known for her many wild statements and strange conversations—here is one with Alice:
“I can’t believe THAT!” said Alice.
“Can’t you?” said the Queen in a pitying tone. “Try again: draw a long breath, and shut your eyes.”
Alice laughed. “There’s no use trying,” she said, “one can’t believe impossible things.”
“I daresay you haven’t had much practice,” said the Queen. “When I was your age, I always did it for half-an-hour a day. Why sometimes I believed as many as six impossible things before breakfast!”
Today I want to talk again about Georg Cantor’s famous proof that the reals are uncountable.
Cantor’s proof reminds me of the above conversation: sometimes I feel like Alice and sometimes like the Red Queen. For many Cantor’s proof is impossible to believe, while for others it is impossible not to believe. Cantor’s proof is correct, but if you have trouble understanding it, or know it is wrong, please keep reading. Please. I would like to engage you.
Actually, there is a fundamental reason to doubt it. Statements asserting the uncountability of certain sets can be formalized in the first-order logic of set theory. But every consistent first-order logic has a model with a countable universe—thus one within which no uncountable sets actually exist. In such a model, everything we think we are saying about the real numbers is translated into an equally meaningful assertion about a set that is actually countable. This is ultimately because in a logical language we can say only countably many things before breakfast, and in a first-order language we can talk about only one thing at a time. We cannot actually say—or believe—uncountably many things before breakfast.
Approaching Cantor’s Proof
Cantor’s proof is strange. It is short, brilliant, important, and yet not believed by some. I find this intriguing: what makes this proof so disputed? What makes it the most discussed proof on the web? In short why is it so hard to believe? See here, here, here, or here for some examples.
But I will say that it is one great results of all time, in my opinion. So I am one of those who do believe in the proof, yet I think we can still discuss this belief, so please keep reading.
The result is of great importance, has a wonderful proof, and has led to many further insights. For instance, the famous result of Alan Turing on the undecidability of the Halting Problem, would be impossible without Cantor’s diagonal method. The same with Kurt Gödel’s Incompleteness Theorems.
Yet Cantor’s proof is special. For such a short proof it certainly has generated a huge amount of controversy. Many people do not believe it, call it nonsense, or worse. Some call people in this category nasty names—I do not think this is right, and I would never do that. I think rather there is something deep going on here. I wonder if the reason so many do not get the proof, is a symptom that we do not explain the proof well. I have tried several times before to discuss this result—see here and here and here.
In the remaining discussion let’s call those who believe the proof Uncounts and those that do not Counts. The names are selected to reflect what they believe: Uncounts believe that the reals are uncountable and Counts that the reals are countable. I am an Uncount, but being a Count is pretty good.
I am always very sensitive to those who misunderstand something: if this happens in one of my classes, I almost always assume it is my fault, not theirs. I once carried this perhaps too far, while teaching a class on complexity theory. We were about halfway through the semester, when a student asked a question that was essentially: what is a Turing Machine? I immediately said: oh, good question—my usual first words. Then as I started to answer the clearly very confused student, the rest of the class yelled:
Are you kidding?
They were mad that a student could ask such a question after hours of lectures on Turing Machines.
The Proof
I will not repeat the famous diagonal proof. See here for a nice explanation. I assume both Counts and Uncounts know the proof. Of course the former do not believe it and the latter do.
Beyond The Proof
As an experiment let us assume that the reals are countable—that is, that Cantor is wrong. That there is a function
that is onto; recall this means that the range of the function is all of 
that includes every real number at least once. The list includes all the rationals, the number 
What I am curious about is what would it allow us to do? Would it really matter, or would it not change our understanding of real numbers, of analysis, of mathematics? Perhaps this is one of the reasons that people do not think that the proof is correct?
As stated above, we know there is an NCW if first-order set theory is consistent. If. We have recently covered the even simpler doubt about Peano Arithmetic being consistent. If we can overcome that doubt, what is easy to say about NCW’s?
Lebesgue Measure
Henri Lebesgue defined his famous measure on sets of real numbers, which is quite constructive, see here for a quick overview. Technically this measure is a map from certain sets of real numbers 
for any disjoint measurable sets of real numbers. This is the property of countable additivity. The construction of Lebesgue measure starts by defining the measure of an interval ![{[a,b]}](https://s0.wp.com/latex.php?latex=%7B%5Ba%2Cb%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002)
where the sets need not be disjoint, but must be measurable.
Now this is a problem for Counts, because this leads to a contradiction. The key is that 
![{\mu([r,r]) = r-r = 0}](https://s0.wp.com/latex.php?latex=%7B%5Cmu%28%5Br%2Cr%5D%29+%3D+r-r+%3D+0%7D&bg=ffffff&fg=000000&s=0&c=20201002)
are all the real numbers. This shows that
But this is impossible since 
![{[0,1]}](https://s0.wp.com/latex.php?latex=%7B%5B0%2C1%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002)
![\displaystyle \mu([0,1]) \le \sum_{k} \mu(\{a_{k}\}) = 0,](https://s0.wp.com/latex.php?latex=%5Cdisplaystyle++%5Cmu%28%5B0%2C1%5D%29+%5Cle+%5Csum_%7Bk%7D+%5Cmu%28%5C%7Ba_%7Bk%7D%5C%7D%29+%3D+0%2C+&bg=ffffff&fg=000000&s=0&c=20201002)
but ![{\mu([0,1]) = 1}](https://s0.wp.com/latex.php?latex=%7B%5Cmu%28%5B0%2C1%5D%29+%3D+1%7D&bg=ffffff&fg=000000&s=0&c=20201002)
This seems to be a spot of trouble for Counts. If you claim that the reals are countable, then you must reject Lebesgue measure. But there is no diagonal proof inside the construction of the measure. This seems to be a problem—what does measure theory look like in an NCW?
Baire Category Theorem
A basic result about the structure of the reals is called the Baire Category Theorem. It is named after René-Louis Baire who proved it in his 1899 Ph.D. thesis.
A set of reals is called first category if it is a countable union of nowhere dense sets; otherwise it is of the second category. Thus if the reals are countable, then they form a set of first category. This follows since the sets 
But, Baire’s theorem is:
Theorem: The set of all the reals is of second category.
This follows since the reals form a complete metric space.
Again this seems to be a spot of trouble. If you are a Count, then this theorem must be false. Or it must be false that the reals are a metric space, or that the reals are complete. But the reals have a simple metric, the distance from 
Another Consequence
The Counts have one very neat positive result that cannot be proved in basic set theory. They can prove that the real numbers are well ordered. A set is well ordered by an ordering provided every non-empty subset has a least element. The natural numbers are well ordered by 
In the NCW the Counts can prove this immediately. Let 
Thus, the real numbers have a well ordering: it is just the above 
Open Problems
Does this help? Have I shed any new light on the issues? I doubt that any Count is now converted to an Uncount, but I certainly hope that I have not converted any Uncount to a Count.
I’m just going to leave this here… http://en.wikipedia.org/wiki/Subcountability
Curiously, judging from mere two of the articles of doubters that you linked, I dont think counts really have any special belief about the countability of reals. They’re having problems with the reductio ad absurdum argument. And I am not claiming they don’t know what a reductio ad absurdum argument is, but that an infinite version of it gets too confusing. The line of thought seems to be “you cannot tell me that once I give you a bijection between natural numbers and reals, you’ll defeat me (show me the bijection is wrong), because I cannot *give you* the bijection. I either cannot start it or I cannot finish it! How will you defeat something I cannot start or finish?”
Well, I don’t know every problem that people have with Cantor’s argument, but I do know that lots of people find reductio arguments completely confusing — even “finite” versions. For another example, a common proof that the square root of 2 is irrational starts out by assuming that it is a rational number a/b in lowest terms, and then shows that it really wasn’t in lowest terms. The reaction of many people to this is, “Well then, *put* it in lowest terms.”
Oh boy. Where do I start?
“Note, the rationals do not form a complete metric space.”
Circular argument. If |N| = |R|, then what?
You’re comparing generators, not the sets. It’s always the same flaw everywhere. Use the same generator for N and R and you have no choice but to have a one to one mapping because the elements must be formed in pair-wise sequence. This is actually Cantor’s first argument, but he botches this as well by not remapping the naturals at each step while allowing arbitrary remapping of the reals (from his previous steps). Reassign the representation that you give the naturals. Each element is immutable, but why do the representations have to be when you generate new numbers?
A real number is defined by an infinite sequence of binary 1’s and 0’s after the decimal point. We’ll using strings for now, but the point is the same.
So if I have an infinite binary tree and choose ONE random path down that tree, I will pick a random number from all possible reals. Ok so far? Here’s the thing though. Every row has finite nodes (that contain each of the 0’s and 1’s as you travel down the binary tree). The first row has 1 node. The second has 2. The third has 4. The fourth has 8. And so on. We have 17 nodes so far. We can keep counting. The nodes are countable.
The distinctiveness of reals is based on the distinctiveness of at least one digit from each real. Cantor uses this VERY notion in his diagonal proof. So each segment (connection) from parent node to child node maps one to one with the child node. If every real must differ by at least one digit, then every path must also differ by at least one segment between parent and child node. This means that the cardinality of all the paths is limited by the cardinality of all the nodes.
The nodes are countable. Since the cardinality of reals/paths is limited by the cardinality of the nodes, |R| = |N|. There’s no way around it.
The flaw in Cantor’s diagonal is simply that at each digit, he has twice as many rows as he’s already dealt with. He can NEVER reach all the elements in the list that anyone gives him. Think of it like this. For every rock that you pick up, you throw two in front of you. Even if you do this infinitely many times, you’ll never pick up all the rocks (change in generator). You’ll still have infinitely many to go. In a way, this is similar to comparing the rows vs. the nodes. They use two different generators and have different mappings between each other. But different generators do not imply a difference in cardinality. We already know that the rows are countable. And we already know that the nodes are countable. So right there, Cantor’s proof is using a bogus technique with the diagonal.
For example, is the cardinality of all the digits of the naturals (in binary, if we strung along each natural end to end) the same as the cardinality of the naturals they represent? Of course! But Cantor says NO!!! He says that they are UNCOUNTABLE! Cantor says that only the MAXIMUM amount of digits needed to represent any given natural in all of N maps one to one with the naturals. So the answer to the question at the top of this paragraph determines your answer if you’re a Count or an Uncount.
no = Uncount, yes = Count.
About “measure”, you’re confusing the generators for the elements. IOW, you’re intentionally denying the remapping of the naturals while allow arbitrary remapping of the reals at each step. Leave aside the immutability of the element REPRESENTATION, but keep the elements themselves, and all of a sudden you’ll be hard pressed to tell the naturals and reals apart.
Indeed, in your construction of real numbers as infinite paths in a binary tree, nodes are countable : they represent the strict subset of the rational numbers that can be written with a finite number of digits in base 2.
> If every real must differ by at least one digit, then every path
> must also differ by at least one segment between parent and
> child node. This means that the cardinality of all the paths
> is limited by the cardinality of all the nodes.
I don’t follow this step of reasoning. What you say is that the fact that two real numbers are different is witnessed by a node. I agree. How does it imply that there are as much nodes as real numbers ? I don’t see why the set of witnesses of inequalities between elements of a set would be as large as that set. Take the booleans {true,false} for example: there are two elements, but the set of witnesses of inequality has only one element (there is only one pair of distinct booleans). Why couldn’t a uncountable set have a countable number of inequality witnesses?
Indeed, the reals do have a countable number of inequality witnesses (if two reals x and y differ, then there exists a rational number r that is a witness for their difference: simply truncate x and y to the first binary digit at which they differ). Thus to witness differences in reals, you only need Q, not all of R.
I think, implicitly, MrX appeals to induction: the cardinality of the reals are limited by the cardinality of the paths for a path already of countable length. So the construction proves that a countable subset of R is countable. I don’t see how it extends beyond the countable subset.
So what you’re saying is you don’t see how Cantor’s diagonal extends to the beyond the countable subset.
You are wrong. Each infinite path can sample into the irrationals. The sample space definitely includes the irrationals. Otherwise, Cantor’s diagonal would never allow irrationals either in the list.
“How does it imply that there are as much nodes as real numbers ?”
Because this is the very notion that Cantor uses. He uses the notion that the diagonal is different by at least one digit from every number in the list.
“I don’t see why the set of witnesses of inequalities between elements of a set would be as large as that set. Take the booleans {true,false} for example: there are two elements, but the set of witnesses of inequality has only one element”
You’re crossing your wires here. Your argument has devolved to there only being ONE boolean value. That’s nonsense.
> You are wrong. Each infinite path can sample into the irrationals.
> The sample space definitely includes the irrationals.
I never claimed they don’t. I only agreed that, in your construction of an infinite binary tree, there is a countable number of nodes. I then added that those nodes correspond to finite paths of binary digits, so can be considered to represent some of the rationals. This is true and doesn’t contradict anything you said before.
> “How does it imply that there are as much nodes as real numbers ?”
> Because this is the very notion that Cantor uses.
I’m not considering Cantor’s argument, I’m considering yours. You wrote a well-structured proof with a reasoning I could follow. I read it and was unconvinced by this step at the middle. I’m asking you how *you* justify this step, not how it corresponds to anything Cantor has done; I’m not interested in Cantor’s proof here. Let me re-quote this part of your proof if it helps make things clearer:
> If every real must differ by at least one digit, then every path
> must also differ by at least one segment between parent and
> child node. This means that the cardinality of all the paths
> is limited by the cardinality of all the nodes.
The way I understand it, you say the following :
1) We can witness each equality between reals (infinite paths) by some node in the tree
2) Therefore, the set of nodes is as large as the set of reals (infinite paths)
I don’t understand how you go from point (1) (which I agree with) to point (2). It is not true in general that the set of witnesses of inequality on a set is as large as this set (see my example with booleans). What would make this particular case true?
gasche: “I then added that those nodes correspond to finite paths of binary digits, so can be considered to represent some of the rationals. This is true and doesn’t contradict anything you said before.”
Oh boy, another one that doesn’t understand infinity. I’m not saying that to be rude. It’s the honest truth and we need to back up and explain why you are mistaken. BTW, any mathematician can explain this to you, so please don’t think I’m the one bringing this up. I’ve already had this part verified, just so you know.
I’ll give you a simple example. Suppose I put one rock down. Then below it, I put two rocks down. Then I put three rock down on the third row. And so on.
If I keep doing this forever, how many rows will I have? It’s obviously |N|. Now how many columns of rocks will I have? It’s also |N| because the number of rocks matches one to one the row position. Yet, there isn’t a single row that has infinitely many rocks. So how is it possible that we need infinitely many columns of rocks? It’s because while any ONE row (one = finite BTW) will have finite rocks, infinitely many rows will have infinitely many columns of rocks.
So what you’re seeing is EACH finite row. But put all rows together and you have paths of infinite length.
Does that clear things up? The fact that I continue and never stop is what makes it infinite. You’re only looking at the finite parts that make up the infinite structure. BTW, Cantor only checks finite digits as well. If we took your argument to heart, then we’d have to conclude his new number is not infinite either.
But hey, if you want to contradict Cantor, be my guest. See, that’s one thing people don’t understand, almost everything that you can say against my setup can also be brought against Cantor’s diagonal. I set up specifically so that it uses most of the same techniques, just in a different setup.
MrX > you obviously do not understand what I wrote. You refute a point of my argument where *I agree with you*. Any node in this tree can be uniquely identified by a finite path, and the set of nodes is infinite and countable. Again, everyone agrees with that, you don’t need to claim that I don’t understand infinity.
I suggest you ignore this part of my messages, and we obviously are talking past each other, and concentrate on my question about the next step of your reasoning, concerning the witnesses of inequality, which I find unconvincing. To make it more precise, I’m talking about what I said in my last message following “The way I understand it …”.
gasche: “What you say is that the fact that two real numbers are different is witnessed by a node.”
This may be the point of confusion. The node is not the witness. It is mapped one to one with the segments. So if you have two segments going down from a parent node, you will also have two different nodes at the end of each segment (one per segment). So the count is equal for nodes and segments. Neither one is a witness.
Also, you see finite paths. But take Cantor’s diagonal. He only checks finite digits. When does he create an infinite path? If I keep checking each path and node that follows from each of the previous paths, then am I not continuing along the infinite path in a manner equivalent to what Cantor does?
You need to ask yourself what constitutes the leap from finite to infinite in a list?
Wow. Just wow.
The size of that binary tree would be
.
Natural numbers are also represented by finite number of 1s and 0s (but maybe I got your argument wrong about that).
The size? What size of what part of the tree? The nodes? The rows? What? And no, it would not be 2^|N| either way. This is why I asked the question. Do you believe that if you strung along the binary representation of all naturals one after the other, would the digits be countable? Yes or no. You’re saying no just like Cantor. I say yes because each natural has countable digits.
“Natural numbers are also represented by finite number of 1s and 0s (but maybe I got your argument wrong about that).”
Each individual natural. But so what? What I’m asking is two-fold. One is how many do you need if I don’t reveal right away what natural number I’m thinking of. This number can be any ONE number from ALL of N. The other is how many digits do you have if you string along all binary representations of all naturals one after the other in one long string?
C’mon. |N| is so clearly equal to |R|, it’s silly. None of the arguments against this I’ve seen so far even make sense.
correction: “each natural has countable digits.” should be “each natural has finite digits”.
“If every real must differ by at least one digit, then every path must also differ by at least one segment between parent and child node. This means that the cardinality of all the paths is limited by the cardinality of all the nodes.”
The binary tree expansion of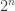
where 
is a (finite) natural number, 
, will give all possible finite sets of natural numbers of size 
for every 
. However, there are also infinite (infinite) sets of natural numbers, such as the set of even numbers, the set of prime numbers, etc. Your binary tree argument of countable nodes does not account for the infinite sets of Natural numbers only finite ones.
Cantor’s proof hinges on the result that the set of all sets of Natural numbers
, which certainly includes also all the infinite sets in 
is not countable. With this result (uncountable elements in 
) one can, then demonstrate a bijection between 
and the real numbers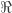 
.
ari: “Your binary tree argument of countable nodes does not account for the infinite sets of Natural numbers only finite ones.”
Oh boy! I’m afraid you have ZERO understanding of infinity. All natural numbers are finite, yet if you continue forever, the list is infinite. So you’re saying that N cannot possibly be infinite because all members are finite. That’s your argument.
Sorry, but that won’t fly with any mathematician. Everyone here seems to be stuck in that they can’t realize that you can form infinite lists where each element is finite. The rows continue, as such it is infinite.
As I’ve said so many times now, if you have a problem with this, then you also believe that Cantor can never check numbers of infinite length because he only check digits located at finite positions. This is the most bogus argument, yet I’m amazed at how often it is repeated.
“This means that the cardinality of all the paths is limited by the cardinality of all the nodes.”
No, it means that the cardinality of all *finite* paths is limited by the cardinality of all the nodes.
Next thing you’ll be telling me that because reals have individual finite digits where you can tell its value, that the real number itself can only have a finite amount of digits. There are infinitely many rows in the infinite binary tree. No path stops at any node.
C’mon. You guys are better than this.
I posited a SERIOUS argument. Please treat it as such.
Wanted to add something. Cantor’s diagonal relies on ONE digit being different from the new number to any given row. In any ONE row, that ONE digit will be different. I’m simply using the EXACT same argument. For two infinite paths to be different, at least one node and at least one segment must be different.
So is Cantor saying that only reals of finite length are different from the diagonal? That would imply that the list only contains rationals. Is this your assertion?
“No path stops at any node.”
Totally agree. Which is a problem on your end because your construction doesn’t count the real paths, only finite paths.
“Totally agree. Which is a problem on your end because your construction doesn’t count the real paths, only finite paths.”
So what infinite path do I not account for when I count ALL the nodes?
MrX: in fact, you haven’t accounted for _any_ infinite paths – just the finite ones. Each node of your infinite binary tree is in 1-1 corresponence with the _finite_ path from that node back to the root – but this says nothing about the _infinite_ paths from the root node ‘downwards’ (that is, the functions from N to {0,1}).
SteveS: There’s no such thing as a digit in a real number located at position infinity. Any ONE digit that you pick from an irrational (or other) real is always located at a finite position. I check every one and that’s enough.
Cantor also checks every finite digit. Do you have a problem with that?
C’mon people. There’s gotta be some better arguments than this trivial nonsense.
“So what infinite path do I not account for when I count ALL the nodes?”
All of them. Your challenge is now to pick any infinite path and tell us the specific index associated with it under your construction.
Delta: “All of them.”
No, I didn’t miss any. Otherwise, you’re saying that an infinite path can be created that doesn’t go through a node on a particular row.
“Your challenge is now to pick any infinite path and tell us the specific index associated with it under your construction.”
So you’re essentially asking me what the last row is and which node on that row maps to each infinite path. Sorry, but that’s just pure nonsense. There is no last row. My argument isn’t set up that way and has no requirement to satisfy your challenge. Nice try though.
Can we end this nonsense now? I’m growing really tired of it.
“This means that the cardinality of all the paths is limited by the cardinality of all the nodes.”
Like everybody already told you, it is here that you are not precise enough.
Come on, if you want people to believe you, just give explicitly the injection between paths and nodes. The one you are trying to construct is not clear enough.
Actually you just say that if r and t are two reals, then their paths are different so there is a node which is different. I agree with it. But what is the node associated with the path of r and the path of t in your injection ? Does it really allow you to distinct all paths of the tree ?
Holf: “Come on, if you want people to believe you, just give explicitly the injection between paths and nodes. The one you are trying to construct is not clear enough.”
Do you agree that there is a bijection between the children nodes and the connection to their parent node? Now, my second question is this. How do you build MORE paths than there are connections when the paths are built from those same connections? How is that possible? It isn’t.
QED
The only objection I’ve received are people who don’t understand the construction. They say that the paths are only different up to a given row. But what they forget is that EVERY row is checked just like Cantor checks every digit. And they forget that a path can only be different if a connection between parent and child node is different. In a way they’re saying, yes, all the paths do cover all of R, but when YOU do it, it doesn’t. BS!
See, instead of rows, consider the binary representations of naturals. If you were to list all natural binary representations in a list one after the other, how many columns (one column per digit) would you need for all of N? You’d need infinitely many columns. No one here seems to grasp that. It is not arbitrary or any such BS. Now, you may ask yourself, wait a second, none of the naturals have infinitely many digits. SO WHAT???? Infinity isn’t a complete number. It’s not finite. If the number of digits required continues to expand forever, than that satisfies the requirement for infinity. Remember, every single natural number is finite, yet the entire list is infinite. Same thing with their digits.
IOW, a finite number of naturals will require finite columns/digits, but infinitely many naturals will require infinitely many columns/digits.
Same principle with the rows in my scenario. There is NO last row. But there are infinitely many last rows. So the width of all those last rows will indeed be infinite and will indeed cover all reals.
Really, the only thing I SHOULD need to prove is that the rows are infinite. That should be enough for anyone to see that |R|=|N|. It’s actually quite a trivial notion. Only thing is that Cantor used a bogus contradiction by comparing generators instead of the elements. So now history has been skewed in an awkward direction.
True or False? You, MrX, can associate any real number (infinite string/sequence of binary 1′s and 0′s) with a unique natural number index.
Real number/sequence
unique natural number 
. Once you provide binary representation of real number I will provide corresponding natural number.
I assume that MrX is the same as MrY? Note again that your allowed real number/sequence fails to account for infinite sequences (ends at b-sub-k); for example, it doesn’t handle the repeating binary real number 0.10101010… (And at the same time you contradict the definition of “natural number”, with arbitrary lead digits, via ellipses out in front.)
I am not MrY.
Delta: “True or False? You, MrX, can associate any real number (infinite string/sequence of binary 1′s and 0′s) with a unique natural number index.”
Not as such in the scenario I have described above. My argument is based on if |N|<|R| and |R|<|N|, then |N|=|R|.
You seem to be dodging the issue though. Why won't you tell me if you believe that the catenation of all binary representations of natural numbers is countable or not. Right there, your answer will determine if you agree or don't agree with Cantor.
“Not as such in the scenario I have described above.”
Well then that satisfies the definition of uncountability.
Delta: “Well then that satisfies the definition of uncountability.”
HAHA!!! You’re so funny. The mapping is done through a two step process. Not through the scenario I set up above. The above process is only about the proof the |N|=|R| through |N|<|R| and |R|<|N|. The mapping you want would not happen in such a scenario and I'd appreciate a little less snark.
1. I think your tone is a bit confrontational and aggressive. That’s not really necessary here, we can all be civil….
2. By definition, if a set is countable, there exists a mapping from the natural numbers to that set. If my understanding is correct, you must exhibit a mapping from the natural numbers to the set of paths down the binary tree in order to prove that it is countable.
And in fact, I claim that there is no such mapping, and I’ll use Cantor’s argument. Suppose your mapping sends 1 to the path (p11),(p12),(p13),(p14),…. Suppose it sends 2 to the path (p21),(p22),(p23),(p24),…. And so on. Each (pnm) in the path represents a choice of going left or right at a node in the tree. If (p11) is left, then let ~(p11) represent right, and vice versa. I claim that the path ~(p11), ~(p22), ~(p33), ~(p44), … is not in your mapping, and that therefore you do not list every path through the binary tree. Proof: Suppose you do. Suppose it is the Nth path in your list. Then (pNN) = ~(pNN), which is a contradiction.
Here is my contradiction to your claim:
> So each segment (connection) from parent node to child node maps one to one with the child node. If every real must differ by at least one digit, then every path must also differ by at least one segment between parent and child node. This means that the cardinality of all the paths is limited by the cardinality of all the nodes.
As you said, the nodes are countable, so let |N| be the size of the set of nodes. Let |R| be the size of the reals (that is, the number of paths through the binary tree). The problem (as someone else has mentioned) is that each node has an infinite number of different reals that differ starting at that node. That is, for a given node n, n is the root of an infinite binary tree, so there are |R| paths that are identical up until n, and then differ. Since this is true for every node n, there are |N|*|R| different paths through the tree. So the fact that real numbers must differ at a particular node doesn’t say anything yet.
As another counter-argument, you say that every path differs from every other path by at least one segment. But I think the same argument shows that every segment has |R| numbers that differ by only that segment, and so you we still have |N|*|R| different paths.
Please let me know what you think or if you find a flaw in my arguments! Thanks.
Not sure if you’re talking to me, but I’ll address the issues anyhow.
1. If so, it’s because people keep bringing up the same tired old issues that are pure nonsense. Most of these questions are meant to troll and sidetrack the issue. They never address the actual topic at hand. So it does get aggravating being trolled.
2. Yes, there must exist such a mapping, but my argument is not based on such a scenario. It is instead based on |N|<|R| and |R|<|N|, then |R|=|N|. BTW, your issue here shows a lack of understanding of the topic at hand if you believe that you can straight up map a finite element to an infinite one. It's the classic Cantor flaw of attributing infinity a finite value.
3. "Suppose you do. Suppose it is the Nth path in your list. Then (pNN) = ~(pNN), which is a contradiction."
No, Cantor can never cross all the elements in the list. Suppose you pick up a rock in front of you and throw two more in front of you. Even if you continue doing this infinitely many times, you still have infinitely many more items to go. IOW, Cantor does not use a one to one mapping that I have given him. He instead skips over elements.
Here's what he's doing. Suppose I give you a list of reals. But I decide what number I'm going to give you. Every time Cantor skips to the next digit, I will swap the current binary representation in my list with another that is all zero's and has a 1 where the digit that Cantor will check is located.
Now, all the elements in my list are still intact. Their order NEVER changed. All I did was swap representations when required. When Cantor goes through infinitely many items, he's only gotten the representations that have a single 1 and the rest is 0's. He hasn't gone through my entire list and can never do so.
So forgive me if I laugh at your clever attempt to go through my list. Cantor uses a different generator. He's proved that his construction uses a different generator than what I'm using. But I've already shown that different generators do not mean that they don't have the same cardinality.
4. "So the fact that real numbers must differ at a particular node doesn’t say anything yet."
Wrong. I use the EXACT same principle as Cantor does. When Cantor produces a digit that is different, he's only proven that his number is different up to that point. The way he attempts to "prove" the rest is by also going through all the rest of the digits. I do the same.
I'm really getting tired of these arguments that Cantor can use a technique, but everyone else cannot simply because you don't like the result.
Tough. But my argument still stands, and yours is rejected. However, if you really believe I can't do this, then you also believe that Cantor is wrong.
So everything you've said is wrong and trivially wrong at that. This is why this is frustrating. There are no serious arguments against my claims.
Hi Mr. X,
I believe your intuition about “tossing two stones ahead” is exactly the intuition behind the reals being uncountable.
The point is not that there exists *some* ordering of the reals such that there is no one-to-one map. Certainly there are orderings of the natural numbers that don’t permit one-to-one mappings; for example, if we list all the powers of two first, and then all of the other numbers later. That’s fine. But *there exists* an ordering of the natural numbers such that there is a one to one mapping between N and N.
Similarly, the claim here is that, for *any* mapping of the reals, Cantor must “toss two stones ahead”. For all mappings of the reals, we arrive at a contradiction. So there is no such mapping over the reals. The point is not that your “two stones ahead” objection might apply — the point is that it *must* apply in *every* case.
Have I interpreted your argument correctly?
I’d like to add one more thing. You have yet to give a formal argument or proof that |R| <= |N|. I believe that my argument above would disprove it, so I should like to see a formal proof if you would like to give one.
bowaggoner: A one to one mapping is a possibility, not a requirement. Cantor maps to a subset of N. Sorry, but your argument is bogus. The subset mapping happens no matter the list you give Cantor.
BTW, why would you even suggest that it’s possible to have a one to one mapping in the first place? You can map base 2 naturals to base 3 naturals, but not if you match digits. Matching digits of a restricted representation NEVER means that the higher base has higher cardinality, but Cantor uses this very flawed principle in his diagonal creation.
My formal argument is that you cannot have more paths than there are segments because the only way two paths are different is if you have different segments. IOW, you can’t have more unique paths than there are unique segments. Since the segments map one to one with the nodes and the nodes are countable, then that’s proof that |N|>|R|. And we know that if |N|>|R| and |R|>|N|, then |N|=|R|.
hi bowanggoner
Yes, I agree there will (I think) be no function whose domain is the set of natural numbers to all possible paths in an infinite binary tree. Another way to to see this is by examining the fractal structure of such infinite beaching tree (which reminds me of the construction of Cantor dust).
However, Mr. X’s construction is very interesting. I agree with Mr. X that using such infinite long paths of an infinite branching structure, lets call them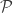
, one could define a bijection between 
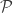and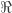 
.
Paths from the root in this infinite branching tree do not form a list. To be clear; each element in a list has to be a finite number of steps away/apart from any other element in the same list. This is not the case with “paths from the root of an infinite binary branching structure” (i.e. elements of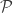
) as between any two such paths there will be infinite other paths by definition.
ari: “Paths from the root in this infinite branching tree do not form a list.”
You’re close. You just need to continue on this train of though. So if R is not represented as a list (I’ve said so many times now), then what’s the other option? I didn’t build that tree for nothing.
hi Mr. X
The implication that “paths from the root in this infinite branching tree do not form a list” (to quote myself!) is that such paths are uncountable.
For a detailed discussion of using lists, as well as functions from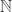
to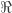 
as equivalent notions of the concept of enumeration or the process of enumerating; see the first and second chapters of Computability and Logic , by G. S. Boolos and al.
However, the fact that one could prove unaccountability of real numbers by showing that the paths of such infinite binary tree can not be transformed into a list, is not an example I have seen before, and it is not one of the examples in the above text. The construction reminds me of Cantor Dust . The proof showing that one can not transform infinite paths from the root of a binary tree into a list, in the sense that this list has a 1st, 2nd, 3rd, …, nth element, and each element is finite number of “places” apart from any other element in the list (well I have not provided one but I believe bowaggoner’s proof probably suffices) reminds me of Cantor’s first theorem of the unaccountability of real numbers, see another of the related entries in this blog, a link to which is also provided in the main body of the this blog by Prof. Lipton.
Sorry did not manage to get some of the links, right, I’ll try again.
hi Mr. X
The implication that “paths from the root in this infinite branching tree do not form a list” (to quote myself!) is that such paths are uncountable.
For a detailed discussion of using lists, as well as functions from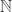
to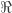 
as equivalent notions of the concept of enumeration or the process of enumerating, see the first and second chapters of: Computability and Logic , by G. S. Boolos et al.
However, the fact that one could prove unaccountability of real numbers by showing that the paths of such infinite binary tree can not be transformed into a list, in the sense that this list has a 1st, 2nd, 3rd, …, nth element, and each element is finite number of “places” apart from any other element in the list is not an example I have seen before, and it is not one of the examples in the above text. The construction reminds me of the Cantor dust/set .
The proof showing that one can not transform infinite paths from the root of a binary tree into a list (well I have not provided one but I believe bowaggoner’s proof probably suffices), reminds me of the Cantor’s first theorem of the unaccountability of real numbers, see: another very interesting entry in this blog by Prof. Lipton, who has also included a link to it in his main text.
oops! sorry again, please replace “unaccountability”, with uncountability, don’t know how to edit comments in WordPress ….
MrY is different from MrX.
, write its binary representation for convenience 
. Write corresponding real number as reverse sequence 
This is the infinite sequence of real numbers. Start testing Cantor theorem. 
therefore, 
, i.e. 
is in the infinite countable subset of 
defined by 
, then define next digit 
, that would select a subset $latex \{ h : n mod 4 = s_{0,0} s_{0,1} \}, etc ad infinitum – infinite recursion. There is no magical last step to infinite representation of string, assumed by Cantor, if it were, then there would be natural number corresponding to real. Now the mapping function is not computable, and if you add restriction for the mapping to be computable, then you go back to Cantor proof.
Ok, from the beggining. Start from the set of all natural numbers
Sorry for being stupid.
The problem with using a binary tree to list all reals, is that certain real numbers, such as π, will never be counted because their digits extend infinitely. Granted, numbers that approximate π will be counted – but π itself will never appear on the list.
Note that rational numbers (even rational numbers like 1.77777…) are a countable set. So the fact that a number’s representation may have an infinite number of digits does not necessarily preclude that number from being a member of a countable set.
Greg: “The problem with using a binary tree to list all reals, is that certain real numbers, such as π, will never be counted because their digits extend infinitely.”
The rows go down infinitely. Each individual digit is located at a finite position/row, including those in infinite length strings. I check them all (infinitely many of them).
If your argument was valid, then you’d have to also claim that N is finite. Do you see why that would be? Individual elements can only be finite (that’s the definition of “individual” = ONE = FINITE). Put all the individual finite digits together and what do you get? INFINITY! YAY!!! Sorry for the sarcasm. But this objection is really getting tiring.
Hi, I read your post and the (many) responses, and I can see how some of the comments posted in response to your construction may have been misunderstood. I like your construction, it is a great place to start when trying to understand the diagonalization argument. You construct an infinite binary tree where each node in the tree stands for a sequence of zeros and ones corresponding to some number. We construct this number by following the path from the root to our particular node and writing a zero if we go left and a one if we go right.
This makes perfect sense. Now, if you have shown that the reals are countable, you must be able to answer a few simple questions about how you count them. That is, you are presumably counting the real numbers in some order. As you suggest, this is quite simple, we can count from top to bottom left to right. So, if you give me a rational number with a finite binary decimal representation like 1/2, I find the node corresponding to the binary representation of 1/2 in the tree and then I count all the nodes that appear to the left and in a higher level of the tree. Perfect. Similarly, given any integer you can quickly find the node in the tree corresponding to it by enumerating the nodes in a similar fashion. Again, easy to do.
Now, I am going to give you a tougher question: Where is the decimal portion of pi in this tree (i.e. what integer does .1415926… correspond to)? If we have indeed counted all of the real numbers, then this should be an easy question to answer. Let’s try the method we used to find the finitely represented rational numbers: I’ll write the binary representation of this decimal, and then I’ll follow this path down the tree. When I reach the end of the binary representation, I can, as before figure out exactly what integer labels this decimal. So far so good, but now I’m stuck. The binary representation of this decimal has an infinite number of digits. So, when can I stop? If this process doesn’t terminate, then what integer do I assign to this decimal? If I cannot assign each real number to a unique integer (and vice versa), then I cannot conclude that the reals are countable. Okay. Maybe we need to modify our counting scheme? But to what? It seems that even if I add this number to my list somewhere that there are still a lot of infinite decimals that I haven’t counted yet. Sounds tricky, right?
Now, I should say that this argument does not work to show that there is NO way to count the reals with integers. We have merely seen that the particular way that you have presented may be incomplete. Cantor’s argument abstracts this process for any method you may give me that claims to count the real numbers.
“Where is the decimal portion of pi in this tree (i.e. what integer does .1415926… correspond to)?”
As I’ve said many times, that’s not the premise of this construction. It’s to show that |R| is bounded by |N|. If you show that |A|<|B| and |B|<|A|, then |A|=|B|.
If you want a mapping, then it's a two step process, and we can talk about that some other time. To start, you can indicate whether or not you believe that if you take the binary representation of all elements of N and write it down one after the other as one long string, are those digits countable or not? This will go further to answer your question than anything I can say. The best part is that most mathematicians don't know what the correct answer is to give the predetermined result they want.
"When I reach the end of the binary representation, I can, as before figure out exactly what integer labels this decimal. So far so good, but now I’m stuck. The binary representation of this decimal has an infinite number of digits."
So you're saying that because each finite digit in Cantor's new number is finite, that his new number is not infinite?
I've asked others and they've never answered. What constitutes the leap from finite to infinite in a list? Each element is finite by definition. Yet the list itself is infinite. Your arguing with me that the list is NOT infinite because each of its elements is finite. Sorry, but you need to go back to the drawing board.
Also, it's all 0's to the left. That's really the path you're indicating when you "stop". It happens to be infinite. There are other paths as well. You're simply confused about the finite-ness of each digit. It's throwing you for a loop. Prove to me that N is infinite by only looking at each element. Then look at your argument.
"If this process doesn’t terminate, then what integer do I assign to this decimal?"
IOW, If this process is infinite, then what finite process will map to it? Remember, this construct is meant to show |R| is bounded by |N|.
And I'm sorry, but I'm not here to teach the difference between finite and infinity.
"If I cannot assign each real number to a unique integer (and vice versa), then I cannot conclude that the reals are countable."
Sure I can. I can show that R is a proper subset of N. That doesn't require a one to one mapping.
"Cantor’s argument abstracts this process for any method you may give me that claims to count the real numbers."
No, he only maps to a proper subset of any list you give him. Tell me what generator he uses to traverse the list and you'll see that I'm right.
MrX:
For the moment, let’s ignore infinite sets. You claim the following:
“As I’ve said many times, that’s not the premise of this construction. It’s to show that |R| is bounded by |N|. If you show that |A|<|B| and |B|= |B| for two sets A and B. |A| >= |B| if there exists an injective map from B to A (i.e. there is a function that maps each element in B to a distinct element in A). That being said, in order to show that |A| >= |B| you MUST provide such a map. For finite sets this definition makes perfect sense and matches our intuition that two sets are the same “size” if they have the same number of elements. (As a side note, recall that A is a subset of B if x in A implies that x is also in B. A is a proper subset of B if A is a subset of B and there is at least one element in B that is not in A. R is not a proper subset of N because clearly there are elements in R that are not in N. However, N is a proper subset of R.)
Now, we take the same definition for infinite sets (we can argue about whether or not this makes sense, but Cantor’s argument is concerned with this definition). This is often a source of confusion for students as we cannot simply “count” the number of elements in an infinite set. With this definition, in order to show |N| >= |R| you MUST provide an injection from R to N. What does such an injection look like? Well, it maps real numbers to natural numbers: each real number is paired with a natural number. As a result, we can think of this injection as labeling each real number with a natural number. Or, as we have discussed in the past, we can think of this injection as producing a list of real numbers such that the ith element of the list corresponds to the real number that it is paired with i under the injective map.
As others have argued above, in order to convince me that Cantor’s argument is invalid, you need only provide such an injective map from the real numbers to the natural numbers. However, I should note that Cantor’s argument claims that it is impossible to construct such a map.
“So you’re saying that because each finite digit in Cantor’s new number is finite, that his new number is not infinite? … Your arguing with me that the list is NOT infinite because each of its elements is finite. Sorry, but you need to go back to the drawing board.”
All I’ve said is that I don’t know how to turn your construction into an injective map. My proposal was to use the decimal expansions of numbers in order to construct such a map, but I observed that such a proposal doesn’t work because it doesn’t tell me how to label numbers whose decimal expansion is not finite. I should note however, that this scheme does allow me to label an infinite number of real numbers; I’m just not sure how to label all of the real numbers. This is a problem with my proposed labeling scheme, and I asked YOU how to fix it. There is no intrinsic problem with real numbers that do not have a finite decimal representation, I simply do not know how to label them with a natural number in a well-defined way from your construction. Perhaps you can suggest a better labeling scheme?
In Cantor’s argument he constructs a real number (with an infinite decimal expansion) by, in some sense, telling me what the ith decimal is. There is nothing wrong with producing a real number in this way (i.e. as an infinite list of finite numbers) as long as the process is well-defined. You are free to do something similar in your construction: you can tell me how to label a real number with an infinite decimal expansion by looking at each digit of its decimal expansion. However, you, like Cantor, must describe exactly how I should do that.
1. There are no finite length reals. What you think is finite has 0’s in the tree all the way down.
2.
Statement 1: Consider the infinite binary tree.
Statement 2: There is a surjection from R paths to the root node connected via nodes.
Statement 3: There are infinitely many segments that go from the root on down for any given real r creating an infinite path.
Statement 4: Set P contains r.
Statement 5: Set S contains all the segments of r.
Statement 6: There is a surjection from the elements of S to r.
Statement 7: For each real s where s is not in P, the path for s must use at least one segment that is not found in S. Add s to P and the associated segments to S that weren’t already in S while creating a mapping from these new segments to s retaining a surjection between S and P.
Statement 8: By induction from base case in statements 3 to 6; and since statement 7 is true for all reals s; and all paths are connected together, then this implies a surjection from all segments to paths, or S to P when P = R.
QED
Let me just take a wild guess at what the objection will be this time. To anyone that has an urge to comment, note that we’re talking about R here, not N.
Sorry, the top of the previous post got messed up somehow. It should read:
“As I’ve said many times, that’s not the premise of this construction. It’s to show that |R| is bounded by |N|. If you show that |A|= |B| if there exists an injective map from B to A (i.e. there is a function that maps each element in B to a distinct element in A)…
The rest is as above.
Oops, it messed up again. It keeps running your quote together with my text. Not to worry, I just stated what the definition of cardinality is directly after your quote.
Lets repeat again for any real number in binary representation
we constructing real number by adding each digit from the right e.g. 
, then 
, at time infinity we get uncomputable index 
.
1) For the argument I was making it doesn’t matter that you can append an infinite number of zeros. Again, I only suggested a scheme whereby you might try to label the nodes. You clearly have something different in mind.
2) Now I want to understand what you are trying to say in the rest of your post. Admittedly, your arguments are not completely coherent, and I’m not sure that I understand exactly what you are trying to say. Mathematics, and proofs require precise language. Please be careful when you correct your statements in your next post.
“Statement 1: Consider the infinite binary tree.”
Done.
“Statement 2: There is a surjection from R paths to the root node connected via nodes.”
I’m not sure what this means.
“Statement 3: There are infinitely many segments that go from the root on down for any given real r creating an infinite path.”
Agreed.
“Statement 4: Set P contains r.”
If by P you mean the set of all infinite paths in this binary tree the I will grant you that for each path there is a corresponding real number.
“Statement 5: Set S contains all the segments of r.”
“Statement 6: There is a surjection from the elements of S to r.”
What is S? I cannot follow the remainder of the proof. If I had to guess what you are trying to tell me, then I would say that you are trying to construct a surjection by somehow looking at the decimal places at which two paths differ. I cannot explicitly say what is right or wrong with that because I don’t understand your construction.
““Statement 2: There is a surjection from R paths to the root node connected via nodes.”
Q: I’m not sure what this means.”
Response: There is a mapping from all the paths to the root node.
—–
““Statement 4: Set P contains r.”
If by P you mean the set of all infinite paths in this binary tree the I will grant you that for each path there is a corresponding real number.”
Response: I’m defining P. It contains r. That’s it.
—–
Q: What is S?
I defined it. It contains all the segments that make up the path r (more broadly defined as all segments that make up all paths in P). Nothing more, nothing less.
—–
You seem to be trying to read into it more than what’s there. At the end, I then show that no matter how many reals you include in P and then put all segments that make up all their paths into S, that statement 7 is true no matter what.
At Oxford in the 1980’s, I took part in a seminar with very strong persuasion to be a Fin.
I think you mean [UltraFin](http://en.wikipedia.org/wiki/Ultrafinitism) not [Fin](http://en.wikipedia.org/wiki/Finitism).
MrX, I sure hope you’re just trolling. By “the cardinality of all the paths is limited by the cardinality of all the nodes”, you’re essentially claiming that if Aleph-Null is countable, then 2^(Aleph-Null) is also countable.
You have no argument. You’re simply incredulous.
Sorry, I thought you were trolling as well. Please accept my apology. Now I’m thinking that you have a misunderstanding of what I was describing. For each path, there are an infinite amount of segments. These segments connect a parent node to a child node. For two paths to be different, there must be at least one segment that is different. These segments map one to one with the child nodes. So the cardinality of the paths (segments that are different) is limited to the the cardinality of the nodes. Because the nodes are |N|, so must the segments. And you cannot have a higher cardinality of paths than the cardinality of segments.
Hope that clears things up. I’m not just leaping from one conclusion to another. I actually created a mapping between the segments and the nodes first.
As I stated above, I don’t buy this argument. Given one particular segment, an infinite number of paths differ at just that segment. So the cardinality of the paths is not limited to the cardinality of the nodes.
bowaggoner: “As I stated above, I don’t buy this argument. Given one particular segment, an infinite number of paths differ at just that segment. So the cardinality of the paths is not limited to the cardinality of the nodes.”
And you’re saying that all those infinite number of paths all use identical segments? How do you tell them apart if not for the segments?
MrX: Well, we need to be more precise about what we mean by segments. I think of a segment as a L or R (left or right). So a path down the tree (a real number) would be represented by a sequence like LRRRLRLLRRLRR….
Now here’s one way to phrase your argument: The segments are countable because the nodes are countable. (Proof: any binary tree on N nodes has N-1 segments, so this follows.) Any two distinct real numbers specified by sequences s1 and s2 differ at some point. (Certainly true.) Therefore the real numbers map one-to-one with the segments. (Highly dubious and thus far unproven.)
My counter-argument here is that every segment maps to an infinite number of real numbers. You haven’t specified *what* mapping you’re using yet, but if you do, I think this can be shown pretty simply.
You may disagree with my representation above. Perhaps you wish to number the segments 1,2,3,4,… in some order. Now you can represent a real number as a list of the segments it passes through, so for example LRR… can instead be represented as (1)(4)(10)….
Again, your claim is that any two distinct paths specified by two such sequences differ at some point, and that this allows us to map the segments to the paths. Again, my claim is that, if you exhibit such a mapping, it can be shown that this mapping sends each segment to an infinite number of paths. However, you have yet to give such a mapping, which would be required to complete your proof as I understand it.
“My counter-argument here is that every segment maps to an infinite number of real numbers.”
That would prove what I’m doing actually. You’re saying that the segments map to something in between R and the powerset of R. It’s not the set of ALL subsets of R. There are no overlaps sideways on the same row, but up and down when following any path, the subsets of R do overlap making the set S (segments) map to A (sets of subsets of R). Now, you can try to claim that |A| <= |N|, but I see no way to do that which doesn't involve proving that the union of infinite subdivisions of R isn't just R itself.
Many people do not believe it, call it nonsense, or worse. Some call people in this category nasty names—I do not think this is right, and I would never do that.
Do you consider “crackpot” a nasty name? I’m a little concerned that you are presenting this as a reasonable debate, when it simply isn’t.
As far as I can tell, the supposed controversy over Cantor’s proof is entirely explained by three facts:
(1) Some people hate impossibility results. Many famous crackpot-attracting topics are impossibility theorems (trisecting the angle, squaring the circle, solving the halting problem), and there just seems to be something about them that draws skeptics who are convinced the received wisdom must be wrong. Sometimes they view these topics as challenges, and they hate what they see as the smug superiority of the people who claim to know they cannot meet the challenge.
(2) Some people have a deep attachment to their own ideas about infinity. In particular, the idea of a single, absolute infinity is extremely meaningful to them, for philosophical or even spiritual reasons. One reasonable reaction to Cantor’s theorem would be to say “I guess my absolute infinity doesn’t measure the size of sets; it must be something else entirely”. Instead, we get a lot of angry reactions along the lines of “if your mathematics doesn’t line up with my philosophy, it has just got to be wrong”.
(3) The proof is too short: it can be explained in a single page and is regularly taught to undergraduates. It’s amazing that something so deep can be proved so quickly, and that tends to increase people’s skepticism. Furthermore, it’s very frustrating to acknowledge that something can be simple and still subtle at the same time; it’s psychological easier to insist that it is wrong.
On point (2), my understanding (which comes mostly from Rudy Rucker’s ‘Infinity and the Mind’) is that Cantor’s theory has an absolute infinity sitting above all the other infinities. Also Cantor saw his ideas as helping him to understand God.
So Kronecker was a “crackpot” ? None of your arguments have any technical merit, but instead are generalizations which are useless in this debate.
Kronecker wasn’t a crackpot, just misguided, since he had the misfortune to live at a time when Cantor’s work had not yet been placed on a rigorous foundation and when its importance in mathematics was not as clear as it is today. Nowadays, there are a handful of non-crackpots who believe in only very weak mathematical systems (e.g., Nelson or Esenin-Volpin), but they are extreme eccentrics, saved from crackpot status by knowing what they are talking about. This is simply not an active or intellectually interesting debate within modern mathematics. There is a near-universal consensus that constructive mathematics is good, that non-constructive mathematics is either good (the majority view) or at least better than nothing, and that which you prefer is a matter of taste.
The reason why my arguments are not technical is that this is not a technical debate. The typical skeptics (i.e., virtually all of them) are not proposing interesting or insightful critiques of Cantor’s argument; instead, they simply misunderstand it or refuse to accept it. From my perspective, the interesting question is why, and this is a psychological question, not a strictly mathematical question.
P.S. To be fair, I once did see an insightful argument from a skeptic (I wish I could find the web site again). He tried to apply the diagonal argument to prove that there is an uncountable number of computable real numbers. Of course it is wrong – the argument just shows that there is no computable enumeration, not that there is no enumeration at all. However, it’s a really clever idea that leads to important consequences, such as the unsolvability of the halting problem. I would enjoy debating skeptics if they all had substantive critiques.
Just a notational note: Might I suggest that “first category”/”second category” be replaced with the more suggestive and less confusing modern terminology (i.e. meagre / nonmeagre)? Especially seeing as Baire’s theorem (applied to the reals) is considerably stronger than just telling you that the reals are nonmeagre, it says that they’re a Baire space.
We can’t say whether or not 2^aleph-0 = aleph-1. I used to think that this was because of a certain vagueness in our understanding of aleph-1, but now I think that its 2^aleph-0 that is difficult to understand. Anyway, I think that countability problems can be better understood by considering aleph-1 rather than 2^aleph-0. aleph-1 is the set of all countable ordinals, and is uncountable, pretty much by definition (otherwise it would be another countable ordinal). Now the totality of descriptions are countable, so we can’t match descriptions to all countable ordinals. But we can – we just have to keep adding to the rules allowed for descriptions. For a fixed set of rules for describing ordinals we can take the set of ordinals described in that way, and so create a new ordinal – which now has a description
Cantor’s proof isn’t in any case a reductio ad absurdum argument. It just says: “Give me a list of reals and I’ll build you one that’s not in it”. If THIS isn’t a constructive argument, then what is?
But I can’t give you a list of “all” reals – can I ? If I did, be definition it would have any real you might want to build.
No you can’t, in virtue of Cantor’s direct and constructive argument.
Actually it’s a mistake to suppose at the beginning of this proof that the given list of reals is complete. If you don’t, then it becomes a very straightforward argument that no list of reals can be complete.
It *is* a reductio ad absurdum argument, and it is *also* constructive. Reductio ad absurdum is just refuting a statement by assuming it and deriving a contradiction, and is perfectly constructive. What’s not constructive is proof by contradiction, where one *proves* a statement by using reductio ad absurdum on its *negation*.
OK, I see. Thank you.
It’s worth noting that while, yes, the real numbers are uncountable in ZFC, some of us think ZFC is a bunch of hogwash. I prefer a foundation more like constructive type theory, but Constructive ZF is okay too.
These theories essentially exploit the fact you mention, “every consistent first-order logic has a model with a countable universe”, to say “well, fine, then we don’t need uncountable sets — let’s design a theory without them”. Here, Cantor’s proof is still valid, but it says that there is no *total* surjection from the natural numbers onto the reals; but it is consistent to assert that there is a *partial* surjection (see http://en.wikipedia.org/wiki/Subcountability ), which we can interpret as saying “there is at most as many real numbers as there are naturals”. And constructively, we cannot turn a partial surjection into a total surjection the same way we can in classical mathematics.
The intuition here is that we are actually dealing with the “computable reals”, of which there is certainly at most countably many, since there are only countably many computer programs (with which to compute real numbers). The partial surjection can be implemented by de-Godeling the natural number to a program which we interpret as a real number. It’s necessarily partial because not all programs can be (constructively) interpreted as real numbers (the halting problem means we don’t know if a program is going to eventually give us another digit, or if it’s just going to loop forever).
So while there are uncountably many reals in ZFC, I take that to mean “Let’s throw out ZFC”.
i think that sometimes you just like turning the crank…
😉
s.
I’ll follow that up by suggesting that maybe the Counts are just constructivists who don’t realize they’re constructivists.
here’s something i just came up with that i rather like, probably because i haven’t carefully checked it.
suppose that the reals are countable, so there is a function r: N -> R that is onto R.
every real k has a preimage under r, call it r^-1(k), or t(k). t(k) can be a set, but it will always have a smallest member, say u(t(k)).
choose any subset of R, say S. look at the set of smallest preimages of S, call it T. Write out T in the following way: each member gets written in unary, with the commas converted to zeroes. Concatenate all of these digits together. Note that this specifies some real number between 0 and 1, written in binary, and therefore has a unique smallest preimage.
So every subset of the reals can be associated with a single integer. so 2^N is no bigger than N. this can be repeated as much as you’d like.
s.
> t(k) can be a set
How could it be a set? If r: N -> R, then r^{-1}: R -> N.
Please correct me if I am wrong.
> each member gets written in unary, with the commas converted to zeroes.
Why would there be commas?
>How could it be a set?
Because in his comment the map r didn’t have to be injective. Assume that r(1)=r(2)=s, then the preimage r^{-1}(s) contains at least 1 and 2.
For simplicity let’s assume r is injective. If I understand steve correctly, the main point is that we can turn a subset of the natural numbers
M={k_n | n \in N}
into a unique real number
s(M)=sum(2^{-k_n} ,n),
which we can then turn into a unique integer again via r^{-1}.
So we have an injective map from subsets of integers to the integers themselves. Which hopefully even a potential Count would consider strange.
yes, and moreover, the chain of powersets all the way up would be countable at any finite height. this should pose some very serious soul-searching for a Count.
on another note:
you can map the reals between 0 and 1 to the powerset of N as well — write such a real in binary, and use the sequence of 0-separated 1’s as instructions for which integers to choose in the associated subset of the integers. pick the number of consecutive 1’s as the offset into the integers for the next element of the subset:
.01101011010… -> {2,3,5,6…}
to avoid chicanery surrounding an infinitely long string of 1’s, you can specify that the first integer you count from is 2, rather than 1, and an infinitely long string of 1’s gets mapped to 1 (it will always terminate the sequence, so you can invert the mapping easily):
.0110101101011111111… -> {1,3,4,6,7}
this seems to work, but again, i haven’t carefully checked it.
s.
Speaking as an interested layman with some background in matters of things like this, my gut feeling against Cantor is because of intuitionism or something as described in the “fin” link above. The whole intuitionist movement idea. If there is no real infinity, then we are just tossing around finite strings of symbols denoting things we label infinite. They may well be logically derived, but the idea of producing a whole infinite sequence seems somehow inconsistent in itself. I consider myself an UNCOUNT, but if I was to be convinced otherwise the other position I think wouldn’t be COUNT as is but something more like FINITE. So there is one anecdotal report …
> If there is no real infinity
Why, there are several real infinities there 🙂
(“real” – existence of which can be proven in some theory)
What about Cantor in FINITE domains? I am Uncount, but would like to be “Nonpoly” or the like. Having a countable set A of infinite binary strings, Cantor constructs a binary string (a “1-limit” for A) which lies outside A, but cannot be determined as not belonging to A by looking at all but one of its bits. Since computations of a circuit are also strings, it would be desirable to have finite versions of his argument to show that small circuits must make errors. Does somebody knows results in that direction?
Among a few results I know is the following. If A is a set of more than k^r binary vectors with exactly r ones, then there is a vector b (a k-limit for A) with at most r-1 ones which cannot be determined to lie outside A by looking at k of its bits.
I have a (quite possibly naive, or even stupid) question:
if one can use one infinite natural number to depict an irrational number.
why can’t all irrational numbers be depicted by infinite natural numbers?
if one can claim to be able to count infinite natural numbers, then why can’t one equally claim he can count irrational numbers?
There aren’t any infinite natural numbers, they’re all finite. Natural numbers are things like 1, 2, 18544 and 289374389578943758942375894230758942375892734672472346723467236472674637642733764273647263746743. Some of them are big, but none of them are infinite.
What is the question referring to? I have not found a reference to ‘infinite natural numbers’ above. There was a reference to infinite binary (or decimal) strings, they are routinely used to represent irrational numbers, for example 3.1415926… (you know which irrational I am thinking of).
Natural number, however, are only represented by finite strings of digits.
An infinite length number does not represent ONE number. It represents infinitely many. Even the irrationals represent infinitely many numbers. No matter what digit you calculate, you cannot differentiate it from other numbers until you process infinitely many digits. So to match an irrational number at every step (these would be rationals), you can’t have just one natural mapped to it.
Short story is that while one natural number can’t map to infinitely many reals, infinitely many naturals can map to an irrational number and all rationals made up of fewer digits. With that, you can complete the mapping. There are infinitely many proper subsets of N that together map to N.
So all those people that ask what natural number maps to PI are really ignorant of what infinity really means. You can NEVER give me the entire irrational number. But a natural number doesn’t have that option. And this is where the bogus contradiction comes from and why the Uncounts seem so smug.
Are you claiming that π is not a real number? How about 1/3? I cannot give you an exact decimal representation of either number, so is neither number a real number?
If you are claiming that only those numbers with an exact decimal representation are “valid” numbers, then yes, you would be correct that such a set is countable – but such a set would necessarily exclude irrational and transcendental numbers – because neither of those two kinds of numbers have an exact decimal value.
“Are you claiming that π is not a real number?”
Uh, no. I’m claiming that there are infinitely many numbers that can be produced with finite length strings of digits based on the initials digits of PI. Not true of any natural number. That disparity must be accounted for in some fashion if there is to be a one to one mapping.
So what I’m saying is that when it comes to mappings between N and R, irrationals should not be treated as a single number, but rather infinitely many.
The Bulletin of Symbolic Logic
Volume 4, 1998
An editor recalls some hopeless papers, by Wilfrid Hodges, pages 1 – 16.
Starts out:
“I dedicate this essay to the two-dozen-odd people whose refutations of Cantor’s diagonal argument (I mean the one proving that the set of real numbers and the set of natural numbers have different cardinalities) have come to me either as referee or as editor in the last twenty years or so. Sadly these submissions were all quite unpublishable; I sent them back with what I hope were helpful comments.”
It is worth a read …
Ian, it is a thought-provoking exercise to read Wilfred Hodges’ essay concurrently with Haruki Murakami’s 2009 Jerusalem Prize Lecture titled Always on the side of the egg, which includes the now-celebrated passage:
From Hodges’ essay one could very easily come away with the impression that mathematics is solely about the “high solid wall” of rigorous logic. Whereas essays like Murakami’s (along with similar-themed essays by accomplished mathematicians like Bill Thurston and Doron Zeilberger) remind us that at the beating heart of every creative human enterprise — most definitely including mathematics — reside “eggs” of human understanding that “we see with our own eyes and touch with our own hands.”
For this reason, I am reluctant to have the last word relating to mathematical cognition reside with either Hodge or with Murakami/ Thurston/ Zeilberger; rather ongoing dialog seems best.
I am quite suspicious of your claim that the construction of Lebesgue measure doesn’t use the uncountability of the reals. But let me think about the Baire category theorem in this regard. Your Baire category proof of the uncountability of the reals would go something like this. By the Baire category theorem, a countable union of nowhere dense sets can’t be all of
. But a singleton is nowhere dense. Done.
Count would then quite legitimately ask why a countable union of nowhere dense sets can’t be
. OK, you say, I’ll prove it. Take the first set. It misses some closed interval of positive length. Now take the second set. It misses some closed subinterval of the first set, again of positive length. Now continue this process. The intersection of the nested intervals is not in any of the sets.
But that argument is convincing to somebody IF AND ONLY IF Cantor’s diagonal argument is convincing to them. I claim that any (wrong, but that’s not the point) objection to one can be translated into a corresponding objection to the other. For example, the objection that “You could take the diagonal number and add it to the list” becomes, “You could take that number you’ve found in the complement of the union of the nowhere dense sets and add the set of all other numbers to the list of nowhere dense sets. And so on.
I’d be very surprised if something like that isn’t true of the Lebesgue measure argument as well.
Occasionally I’ve found myself arguing with Count people. My usual opening gambit is to ask them to tell me what bijection between
and 
they have in mind. That ought to settle the argument very quickly, but of course it doesn’t …
Yes, let’s not forget the Cantor’s original argument went more like that! But I’m not sure that if and only if is correct; this argument doesn’t require first establishing a bijection between R and P(N). Though I’ll admit I haven’t previously encountered Counts who claimed that there was a problem with the bijection between R and P(N), or who insisted that P(N) was countable rather than that R was countable, etc. So correct in practice, perhaps?
Oops, I meant take the singleton consisting of that number and add it to the list of nowhere dense sets.
Let me try to engage your gambit :).
For brevity, we can say that well-ordering of R is the same as a bijection from N to R. W.L.O.G we will consider (0,1), and ignore 0.999999…. etc. Now, to get a well-ordering, take a lexicographic based ordering, such that a [ b ([ is out special operator denoting <) if |a| < |b|. ie; 0.1 < 0.01. If |a| = |b|, then a [ b if a < b (this takes care of the case where there is infinite numbers – they have to be different from each other at some finite point).
Now, the ordering is 0.1,0.2,0.3,0.4….0.9, 0.01,0.02, …0.09,0.11,0.12……..0.99, 0.001,0.002 ……
“My usual opening gambit is to ask them to tell me what bijection between and they have in mind. That ought to settle the argument very quickly, but of course it doesn’t …”
I`m a Cantorian, but is there an explicit known bijection between the rationals and the naturals? Just asking.
Johan
Yes there are explicit maps from N to N x N which essentially solves your question. They are called pairing functions….should be able to find.
Sorry, I forgot to say that the mapping should well order the rationals. I found the answer already.
Gowers,
I believe the uncountable nature of the reals is used implicitly in these theorems, but it is not as explicit. Also I wanted to make the point that there is some consequences to being a Count.
Let me continue to play devil’s advocate for a bit.
It’s incredibly unlikely that a Count would understand enough about Lebesgue measure to feel the force of those consequences, but it’s interesting to fantasize about the possibility. I think if you believe that the reals are countable, you won’t be troubled by the fact that there is no countably additive measure on the reals, any more than conventional mathematicians are troubled by the lack of a translation-invariant probability measure on the integers (which is sort of annoying, but we learn to live with it). I think Counts would simply say “zero times infinity can be anything you like”. We’ve got very used to thinking that zero times a countable infinity is zero, at least in this context, but Counts don’t recognise the distinction.
Note that Counts can still say quite complicated things like that the Cantor set has measure zero. Why? Because we all agree about measures of unions of finitely many disjoint intervals, and the Cantor set is contained in arbitrarily small such sets. We can’t say the same of the rationals.
What about taking binary representation of real number in the interval [0,1) and it reverse representation of the natural number e.g 0.101001….
[0,1) …100101 
?
Hi, you cannot do this because some irrational numbers have literally infinite binary representations, and so it does not make a natural number in in N. (Every number in N is finite.) Hope that helps!
It doesn’t really ‘help’. You’re saying that numbers can be expanded infinitely to the right but not to the left of the decimal place? Pi may be infinitely far down my list but my list is infinitely long so keep looking, you’ll find it. Hope that helps…
Hi clmolv, we’re talking about mapping a real number, like .2301923890133…., to an integer, like 74. Real numbers may be expanded infinitely to the right of the decimal place, but integers cannot be expanded infinitely to the left.
> Pi may be infinitely far down my list but my list is infinitely long so keep looking, you’ll find it.
You seem to be talking about a different issue here? In an infinitely long list, every particular element is located at a particular (finite) index in the list. That is using the common definition of a list, which is pretty much a mapping from the natural numbers.
This is part of what bothers me. A real can be expanded infinitely to the right but integers cannot (each must be a finite representation, which will never get you even the tiniest fraction closer to what the infinite numbers that are contained there, ie. any finite number will always be about 0% of the infinite number in N regardless of how many finite elements it may have).
I have come to (in my little, bogus mind with little math education – hope that satisfies Uncountables) that I see Reals as a clever method to approach dividing something composed of infinitely many elements, in a way that makes practical sense, however confusing infinity may be.
For example, PI a label for an exact quantity (or proportion) that nobody can ever properly size, or accurately describe, except as an approximation…like a drawing, or an ever growing list of details we call the digit of PI.
They represent 3 full units, each composed of infinitely many elements, as the rational part if infinite. And then, an exact proportion of a remainder full unit – always ever-improvable proportion by the digital representation of that rational part (with the true rational component requiring an infinite number of digits).
The Rational part of the constant e, 0.7… Is also something that we know is an exact proportion. And that unfortunately requires infinite digits to represent it accurately. Yet, the rational part of e is clearly larger than that of PI. But in all these cases it’s in reference to a hole, the 1 pie that is being divided in infinitely many pieces to accurately describe a rational. So the notation, carries the notion of it’s reference to a pie being divided with infinite accuracy. But could you ever tell how many elements you need to represent those proportions with accuracy? Obviously, infinite. But since the cuts represent infinite accuracy in cutting the pie starting at arbitrary entry points (ie. The decimal approach allows to traverse the infinite set of elements as a Proportion of the total, just like you could select any part of an Album in the old vintage records instantly without traversing the 45 mins or so), they allow for something Naturals are not allowed to do.
But let’s suppose we have PI, and find a way to assume we have the infinite number of digits of its rational part described. Then if we could think that this can be described by a proportion and specific – yet infinite- amount of Rocks that rational part of PI represents of the full pie it’s cutting. However, each set would be countable with uncontably many. You just count rocks, and each set acts like N. However, if you ask how much each rock must represent as a proportion of 1 (the full pie), the answer must be 0%. Which is kind of upsetting somehow, because though in relation to a total pie, things make sense (or as a proportion), these Real numbers are not numbers, and only proportions (rational or irrational).
If you add infinite rocks to PI, one by one, you never get any closer to say the Rational part of constant e. Or any other rational. The Reals have units if infinitely small size that only make sense as ranges, and can only be used by analogy to cutting a pie or devices like the old record players with a niddle that can be allowed to skip entire ranges.
The naturals, if you think there is an infinite number of them, do they make a hole? Do they have any relationship to the equivalent of a pie? If not, then that infinity is smaller. Or more precisely, you are not allowed the benefit of constructing infinitely large integers – each must be finite. But if you think of these integers as, when taken to infinite, they fill up a space that can be considered a pie (of intinite elements), and allow them skip hole regions, then it’s akin to saying you invent naturals that behave as proportions, and in that case, they would be Reals.
Somyes, the thing that is becoming to me a little obvious, is that indeed the “generators” are different, and that’s the hole point, regardless of which infinity is larger.
Do I believe one is larger than the other? No. Just like the naturals are designed to be an evergrowing number of elements starting from individual Rocks, Reals are infinite precision cuts that describe proportions. A Rational component, at the absolute precision level, only has quantities in relation or proportion to the pie. They ultimate cannot relate to number of elements (like naturals to Rocks), as they only bear sense in relation or proportion to the pie (or big 1, or the infinite amount of elements in that group). And as such, you can add only proportions in relation to a whole, as any individual addition at the infinite level of precision will amount to nothing, in proportion to the pie).
They both have the same infinities, N, and R.
Now if you think of PI, it has a natural part, and a rational part. So you can combine both. We know 3 makes sense, because we know what 3 is here. It describes the integer compnent of relations between circle elements. And the rational part requires an infinite precision cut. And the entire number makes sense. However, the pie subdivision cannot have units, and the naturals can spik the queue.
Aside from Dick’s opening reference to Lewis Carroll, no-one has mentioned the rich comedic opportunities associated to Dick’s question. Rudy Rucker’s novel White Light inverts Dick’s hypothesis to read “What If Cantor’s Proof Were Easy to Verify?”
Many propositions of arithmetic and geometry are easy to check by direct physical experience (we can verify by counting on our fingers that 3^2+4^2 = 5^2, we can draw the associated triangle and verify that it is a right triangle). Similarly, in Rucker’s White Light world it is common practice to verify Cantor’s Proof by checking into Hilbert’s Hotel, or start a manufacturing business using the Banach-Tarski Theorem.
Rucker’s novel is mathematically disquieting (and thus funny) because it shows us that Cantor’s theorems are fragile in a way that Pythagoras’ aren’t, namely, they lack a robust suite of verification procedures.
But perhaps this view is mistaken. Consider for example:
Would would students learn from this assignment? The entropic grading method is objective, but is it fair, and if not why not? What is your personal estimate of the six-theorem entropy?
Needless to say, this imagined assignment is very largely inspired by Doron Zeilberger’s wonderful essays and teaching. 🙂
John,
Speaking of humor, I suspect this story about Dodgson (aka Lewis Carroll) is fairly well known; but for the folks who may not have heard it:
“The story is told (which Dodgson always denied) that Queen Victoria was so enchanted by the ‘Alice’ books that she asked for his next book to be sent to her. When she was handed Dodgson’s ‘An Elementary Treatise on Determinants’, she was not amused.”
Slight confusion – a well ordering will imply a bijection between R and N. But doesn’t the well ordering principle (ZFC + axiom of choice) mean that there is a well ordering to even R ? Granted, we can (perhaps) never find the ordering – but doesn’t the fact that it exists, means that R is countable.
Or should I interpret countable as a set which has a computable well-ordering ..
A bijection between R and N implies a well-ordering of R in an easy way. The well ordering theorem deduces it from much harder arguments, leading the conclusion that a set does not have to be countable to be well-ordered.
This is, perhaps, a point to test: is it also difficult for some students of set theory to accept that there are well-orders bigger than omega (the order of the natural numbers)? This does not involve uncountability or diagonalization. But it does stand in some contradiction with our daily experience, doesn’t it?
My apologies, Professor, but it was the White Queen.
Thanks for the article! Very interesting!
Don’t apologize, bowaggoner; this misattribution needs to be fixed!
Wilfrid Hodges’ “An editor recalls some hopeless papers” is a nice discussion of this:
http://projecteuclid.org/euclid.bsl/1182353548
Wilfred Hodges’ essay — written in his position as the editor of The Journal of Symbolic Logic (JSL) — is lucid and compelling (a Google search finds the complete text). Only one step remains, which is only a minor cosmesis: change the name of JSL to The Journal of Non-Experimental Symbolic Logic (JONESYL).
Once readers thoroughly appreciate that theorems proved in JSL/JONESYL are distinguished from the theorems of the rest of mathematics, in being insusceptible to Zeilberger-style experimental mathematical testing, then the puzzlement and even incivility that has attended so much of the discussion here on Gödel’s Lost Letter no doubt will swiftly fade away.
With JSL/JONESYL leading the way, the editors of journals on oracle-defined complexity classes will follow in clarifying the role(s) of verification and validation, and perhaps increased humility in this regard will extend even to the physics journals. And thus will dawn an enduring era of mathematical harmony and understanding, eh? 🙂
I am neither a Count or Uncount, though I am more or less convinced by Cantors proof.
Hower, Cantors proof is a second-order proof, because it postulates the existence of a function, so I don’t really see any point in invoking Skolem here.
Wow, I didn’t expect this post to generate such a nice big discussion, thanks a lot everyone!
It seems to be bigger than even NP=?P blogs!!
With a title like “What If Cantor’s Proof Is Wrong?”, I think you are setting yourself up for the most comments ever for a post on this blog.
Cantor’s Theorem is the one theorem that people love to hate. Here’s my favorite argument against it.
Suppose that $2^{\aleph_0}>\aleph_0$: This implies that $\aleph_0 = \log (2^{\aleph_0})>\log(\aleph_0)$, where “log” (base 2) is the inverse of the “2 to the power” function generalized for sets of infinite cardinality. Then if $\log(\aleph_0)$ is an infinite cardinal number, then $\aleph_0$ is not the least infinite cardinal number, which contradicts the definition of $\aleph_0$. And if $\log (\aleph_0)$ is a finite number, then $2^{(\log (\aleph_0))}=\aleph_0$ is a finite number, which contradicts its definition too. Therefore, $\aleph_0=2^{\aleph_0}$. But Cantor’s theorem says the opposite of this! So Cantor’s Theorem must be wrong.
(I’m not saying I agree with this argument, only that I like it the best.)
I’m sorry, I thought this website processes LaTeX. The LaTeX didn’t work.
In fact this argument proves that the naturals aren’t in one-to-one correspondance with any power set. They need another axiom than that of power set to exist, namely the axiom of infinity.
I made up the argument a few years ago and posted it to usenet. I can’t remember why it’s wrong, but I remember concluding that it is wrong. What I like about it is that it seems like it is right, at least superficially.
It’s wrong because log(aleph_0) doesn’t exist: there’s no cardinal X such that 2^X = aleph_0. If you accept Cantor’s proof, this is what your amusing argument proves. 🙂
Serge,
Just to play devil’s advocate, what if we extend the cardinals so that log(aleph_0) does exist? There is a precedent for this, as we know that log 3 doesn’t exist in the rationals, but it does in the reals, for base 2. Then how would my argument be wrong?
Anyway, this stuff is to me just fun. I don’t believe in infinity anyway.
log 3 doesn’t exist in the rationals like log(aleph_0) doesn’t exist in sets – you’ve just proven this. They enlarged the notion of number by inventing the reals, so you’ll have to enlarge the notion of set. Good luck. 🙂
I “believe” in infinity because it works, it’s useful, it’s fun, it’s beautiful and so on…
I gotta say I’ve had some fun, but was somewhat disappointed by the objections brought up against my argument. I’ve already had all of that confirmed by several mathematicians that I had it right. I did not tell them what I was working on to avoid bias. So they’re actually the ones who gave me their answers.
Again, all the arguments so far have been that Cantor can use a technique, but that I cannot when other mathematicians have already confirmed this part.
If we’re just being fair here, without snark or bias, my guess is that paranoid schizophrenia is more to blame for your orthodoxy than anything else.
MrX, tell me where pi is in your list, or even a simple rational like 1/3, then we’ll talk.
pelotem: “MrX, tell me where pi is in your list, or even a simple rational like 1/3, then we’ll talk.”
Sigh. I cringe when I hear that question. It shows a complete lack of understanding of infinity.
Yes, it shows your complete lack of understanding of infinity, that’s why I brought it up 🙂
pelotom: Whenever someone asks what PI maps to, I cringe. It’s because they’re using a gotcha question to try and stop the conversation. First off, you don’t need a mapping to prove |R|=|N|. You can use the principle that if |A|>|B| and |B|>|A|, then |A|=|B|. I’ve said so from the beginning. So what many people who are biased or brainwashed tend to do is change the topic and ask the question that you are asking. But go back to the very top. Do you think it’s easy being a “count”? Do you think it’s easy to discuss ANYTHING about the subject matter. I’ve show several times the absurdities of the objections like people expecting there to be a digit at an infinite location when that is impossible. So all those people don’t understand infinity. And now you want to talk about a different topic all together. How do you suppose I convey this mapping when I can’t even discuss the above topics with the infinite binary tree where R overlaps N.
If you want a mapping, then may I suggest you look at all the finite subsets of PI. How many are there? |N|, correct? So what do I use for the other reals? The reason I say you don’t understand infinity is because your question amounts to asking what finite elements can map to infinitely many. It is impossible.
However, allow me to propose a different mapping. One a la Cantor where he maps to the sub-elements, aka the digits. I enumerate N in the following manner. The first element has 1 node. The second has 2. The third has 4. The fourth has 8. The fifth has 16. And so on doubling at each element.
If I take the cummulative sequence of all nodes and put them all on a single line, these are countable. But note that if I leave them as is, the nodes match up exactly one to one to all the nodes of the infinite binary tree. So whatever you’re using to differentiate between infinite paths from the root node cannot be more than what is used to differentiate between the naturals.
QED.
So next time you ask that question, tell yourself that you don’t understand infinity and stop. If I’m sounding rude, it’s not my intention. My intention is to be direct because “counts” can never have a real discussion. Can never be taken seriously because of comments and questions like yours.
MrX:
> “Whenever someone asks what PI maps to, I cringe. It’s because they’re using a gotcha question to try and stop the conversation.”
I’m not trying to stop the question, I’d just like an answer to the question.
> First off, you don’t need a mapping to prove |R|=|N|. You can use the principle that if |A|>|B| and |B|>|A|, then |A|=|B|.”
What does “|A| > |B|” mean to you when A and B are infinite sets, other than “there is an onto mapping from A to B”? If you agree with that definition, I will agree that “|A| > |B| and |B| > |A| implies |A| = |B|”.
> “So what many people who are biased or brainwashed tend to do is change the topic and ask the question that you are asking.”
Ad hominem attacks distract from your argument, I suggest you don’t use them.
> “If you want a mapping, then may I suggest you look at all the finite subsets of PI. How many are there? |N|, correct?
Please be precise; “subsets of pi” is a nonsensical phrase. Do you mean “subsequences of the digits of the binary representation of pi”? If so, yes, I agree that there are countably many such *finite* subsequences. Once you talk about the infinite subsequences, however, they become uncountable.
> “So what do I use for the other reals? The reason I say you don’t understand infinity is because your question amounts to asking what finite elements can map to infinitely many. It is impossible.”
You’ve lost me here. I haven’t a clue what you’re talking about.
> “If I take the cummulative sequence of all nodes and put them all on a single line, these are countable. But note that if I leave them as is, the nodes match up exactly one to one to all the nodes of the infinite binary tree.”
Every node in the the resulting tree represents a real number, yes, but not every real number is represented by a node in the tree. The reason why is that any node in this tree must have a finite binary representation, which numbers like 1/3 and 1/pi do not. That’s why I asked where they are in your tree, because they’re not.
The only way your binary tree can represent all real numbers is if you treat each (possibly infinite) PATH through the tree as representing a number. There is indeed path for each real number. Unfortunately set of possible paths in an infinite binary tree is uncountable, so you’re back to square one. The set of nodes is countable, but fails to account for all the reals.
pelotom: “Unfortunately set of possible paths in an infinite binary tree is uncountable”
Circular argument.
“The only way your binary tree can represent all real numbers is if you treat each (possibly infinite) PATH through the tree as representing a number.”
Yes.
And I map to all digits of all those paths.
“The reason why is that any node in this tree must have a finite binary representation, which numbers like 1/3 and 1/pi do not. That’s why I asked where they are in your tree, because they’re not.”
But I never stop. I map to ALL digits of PI. This is the EXACT technique that Cantor uses. So when Cantor uses a technique, it’s ok. But when someone else use the exact same technique, it’s not ok? How does that work? Every single ONE of those digits are FINITE. There isn’t a single digit that is infinite in PI. NOT ONE. This is what you don’t get. This is the same old tired and bogus objection that’s been incessantly repeated. And yet, Cantor only uses finite digits as well to differentiate from all other reals. But when I do it, it’s no good? How quaint!
pelotom: I want to repeat that I never stop at any node. If I do map to a rational number, it’s by mapping to all its non-zero digits INCLUDING all its infinitely many zeros which makes that path infinite just like the irrationals. So mapping to a rational is NOT doing via a finite amount of digits. It is done via mapping to all its digits, all infinitely many zero’s as well.
Sorry for the double-post, last one screwed up my formatting…
MrX:
“So mapping to a rational is NOT doing via a finite amount of digits. It is done via mapping to all its digits, all infinitely many zero’s as well.”
Ok. So you are representing each real number by an infinite path through your binary tree. Now describe the mechanism by which you enumerate all paths in this tree. That is, describe an onto function from the natural numbers to the set of infinite paths through this tree. That’s what you are claiming exists, right?
If you claim to have such a function f, then I will show you a path which you forgot to map to. We’ll call this path P. P is defined as follows:
^f(0)(0), ^f(1)(1), ^f(2)(2), ^f(3)(3), …
Note that I’m treating each infinite path as a function N -> {0, 1}, which looks up branch the path chooses at depth n. “^” in my notation means “flip the bit”.
P is a perfectly well-defined infinite path through the binary tree, would you agree?
Now, since you claim your function f is an onto function from the naturals to the set of infinite paths in this tree, that means that any path, and in particular P, must be mapped to by f. In other words, there exists some natural number n such that f(n) = P. So what is the n which maps to P according to f? It can’t be 0, because we know P differs from f(0) at the 0th element. It can’t be 1, because P differs from f(1) at the 1st element. And so on. We are left with the unavoidable conclusion that the number of infinite paths through a binary tree is uncountable.
pelotom: “^f(0)(0), ^f(1)(1), ^f(2)(2), ^f(3)(3), …”
Yes, I understand. So you have a path index and a digit index. The set of digit indexes MUST be a proper subset of the path indexes. For your “proof” to work, you have to prove that they map one to one and they don’t in the context that you’re using them. So if your proof succeeds, it must fail. Your P is proof that you only got a subset of N. It is NOT proof that a one to one mapping cannot exist.
> “The set of digit indexes MUST be a proper subset of the path indexes.”
Why do you say that? The set of digit indexes = the set of path indexes = N.
pelotom: “Why do you say that? The set of digit indexes = the set of path indexes = N.”
Prove it. This is what I don’t get. You just assume stuff that just isn’t so.
MrX:
“So mapping to a rational is NOT doing via a finite amount of digits. It is done via mapping to all its digits, all infinitely many zero’s as well.”
Ok. So you are representing each real number by an infinite path through your binary tree. Now describe the mechanism by which you enumerate all paths in this tree. That is, describe an onto function from the natural numbers to the set of infinite paths through this tree. That’s what you are claiming exists, right?
If you claim to have such a function f, then I will show you a path which you forgot to map to. We’ll call this path P. P is defined as follows: . Note that I’m treating each infinite path as a function N -> {0, 1}, which looks up branch the path chooses at depth n. “^” in my notation means “flip the bit”.
P is a perfectly well-defined infinite path through the binary tree, would you agree?
Now, since you claim your function f is an onto function from the naturals to the set of infinite paths in this tree, that means that any path, and in particular P, must be mapped to by f. In other words, there exists some natural number n such that f(n) = P. So what is the n which maps to P according to f? It can’t be 0, because we know P differs from f(0) at the 0th element. It can’t be 1, because P differs from f(1) at the 1st element. And so on. We are left with the unavoidable conclusion that the number of infinite paths through a binary tree is uncountable.
pelotom: If you use a “flip the bit” technique, you can only get a subset of N regardless of what the function f is. The number of bits is a proper subset of N.
“In other words, there exists some natural number n such that f(n) = P.”
I’m mapping to all nodes in all paths. I’m using Cantor’s technique of mapping to all digits, or in this case all nodes of all rows.
“We are left with the unavoidable conclusion that the number of infinite paths through a binary tree is uncountable.”
No. That’s silly. You ditched f and used your own subset of N. It’s expected that P will be different than all element in your subset. But it IS in the original set.
MrX:
I’ve puzzled over your objection for several minutes and find it to be utterly unintelligible. If you care to reformulate it in precise terms I will read it, but otherwise I have nothing further to say beyond the proof I’ve already given.
pelotom: Back to the PI thing? Look, it makes you sound ridiculous. It’s a gotcha question that only serves to distract. I’ve explained why a million times over. It is no surprise you don’t understand it. You don’t want to. First, it’s not the technique I’m using. Second, you persist with this nonsense even after telling you that it’s not the technique I’m using. Third, you think there are digits at an infinite location. Why should I bother with such silliness?
“Third, you think there are digits at an infinite location.”
I think no such thing, nor have I ever said so.
pelotom: “I think no such thing, nor have I ever said so.”
Then what’s the complaint about my mapping to digits all about? They’re all finite. If a digit at an infinite location isn’t the problem, then what is it exactly?
.
I agree with the anonymous commenter above, that while it is right and polite to refrain from calling Counts nasty names, I’d suggest you may have taken a step too far in dignifying their position, and risk giving a passing uninformed reader the misleading impression that there actually is a reasonable debate to be had here.
If someone doesn’t like Cantor’s theory of transfinite numbers, there are various philosophical exits available to them, in the form of intuitionistic logical frameworks which deny certain of the premises of Cantor’s theorem. These are coherent and respectable, if rather uncommon, positions to hold.
What is not reasonable – and this is what distinguishes the average Count from a serious Finitist – is to accept the premises of Cantor’s theorem, but deny its conclusion, insisting that the argument contains an error. Because – guess what? – it doesn’t.
(Incidentally, I also agree with bowaggoner, that you have ascribed the impossible Queen the wrong colour!)
Cantor compares generators, not the elements. How is that NOT an error? He cannot traverse the list I give him. He can only prove that his new number is not in a proper subset of the list I’ve given him, but that number IS in my list.
Keep up the good work, Mr X. If you’re able to refute Cantor’s proof within the framework of ZFC, you’ll certainly be awarded the next Fields Medal! 🙂
Groan.
Cantorians make a big error by reversing implication.
From a finite definition like 1/9 we can obtain the infinite string 0.111111111and.so.on. But from such a string we cannot obtain 1/9.
I consciously did not write “0.111…” because this is easily taken for an infinite string which it is not!
You cannot obtain or transfer information from/by an infinite string. You will have to see the “end”-signal. Otherwise you don’t know whether or not a digit 2 will follow behind what you have seen.
Why is this error important? We know that there are only countably many finite definitions like 1/9 or 0.111… . So most of the uncountable set of reals do not have a finite definition. According to what I said above, they don’t have a definition (in the sense of containing informtion) at all. But if so, how should we find a first element of a set of undistinguishable “real numbers”.
Result: The axiom of choice can be used to prove that it is false.
Regards, WM
MrX,
I don’t mean to pick on you, except that you seem to be the most fervent poster arguing against diagonalization.
I think that it would help tremendously if you refrained from the following:
a) Trying to use Cantor’s argument to prove your own. There is a fundamental problem here. If you fully use it, it will be incapable of proving its converse (this is due to implication). Moreover, Cantor is dead. The argument should stand on its own. You don’t ever need to reference Cantor to make your argument, and it only hurts your argument when you do so. You should be capable of proving that card(N)=card(R) without referencing him or his argument. It will be very helpful in your explication if you do so.
b) Making arguments that end with “you don’t understand infinity”. While possibly true, it is vacuous in that it doesn’t proceed in making your argument.
c) To generalize b): To attack the writer. This is flawed and old enough to have a latin name: ad hominem. An ad hominem claim may indeed be true, but it brings up a whole separate set of issues which are unrelated to the main point that you’re trying to make. In other words, stick to the point by addressing the technical concerns exactly.
d) Be as precise as possible. This means defining your nouns. If you say “generator”, explain what you mean. If you don’t have to use a noun to make your argument, don’t. It will make it simpler and easier to understand. If you stick to the terms defined in the problem definition, it will make your argument much easier to follow. We are all basically stupid people and need things spelled out in order to understand them.
e) Stop for a bit and take some time to think about the arguments which claim to refute your argument. Don’t autopost. Stop and think it over. The important thing here is *not* who is right and who is wrong. The important thing is *what* is right and what is wrong. There is a fact of the matter, which we are trying to reach. Which person first correctly explicated the truth of a fact is much less important than the truth value of the fact.
That all having been said, I have a few concerns with your line of thinking as I understand it so far.
True: You can organize the real numbers, R, as a tree. Even a binary tree, if you like.
Not yet established: This means that they are countable.
Diagonalization works because you can explicitly name a member which disproves the conjecture that you could write the real numbers down as a list, with a first member, a 100th member, etc. If you don’t like arguments of this sort, that’s fine. Simply say that you don’t like arguments of this sort. It has a philosophical rationale.
Technical point: I can see how you might think that being able to represent the reals as a tree is similar to representing them as an ordered list (with a specified first member). Think back to the claim. The claim is that card(N)=card(R). The only way to show this is either with an explicit map, or by contradiction. The proof of the converse works (i.e. that card(N) != card(R) ) because if you assume such an explicit map, you can derive a contradiction.
You can either prove *your* claim with a contradiction (i.e. showing that card(N) != card(R) leads to an illogical conclusion) or directly, by explicitly showing the map. Until you have one of these, you don’t have a proof.
steve.
a) I only bring up Cantor because once people see that the technique is the same, but applied in a different setup, they can look at why their argument was wrong. It’s the most effective way to dispel trivial objections. So no, I will not stop doing this. It’s been very effective. You seem to be saying that you want to be able to show how I’m wrong without getting Cantor’s diagonal argument involved. Sorry, but if I use one of the same techniques as Cantor, then we’re either both right or both wrong when someone objects to that specific technique. This is in fact what I despise about most objections thus far. The two faced view that Cantor can do something, but no one else can unless it achieves the predetermined result that you like. Sorry, that’s a non-starter.
Short story, it only helps when I reference Cantor because it keeps the discussion focused and dispels trivial nonsense as early as possible. Note how no one has said that Cantor’s diagonal is not infinite, yet the paths in my setup are supposed to be finite. How does that work when the technique of checking every digit is the same?
b) To those I’ve said so, it’s blatantly true. It’s not meant to be rude. It’s that it distracts from the real issues and it’s always when the SAME issue was brought up countless times. I’d rather dispense with it and move on. I always explain why they were wrong.
c) I can’t always tell when someone’s not trolling after an issues has already been dealt with countless time. Even so, I always explain why their objection is wrong.
d) “If you say “generator”, explain what you mean.”
WHAT??? We’re talking about infinity. You have to know the subject matter. Look up the Peano axioms and Dedekind cuts. There are others that anyone can come up with on how to generate numbers. The generator is also used during traversal of an infinite list. This is all basic stuff. I can’t be describing basic knowledge all the time in small comments that end up too long anyhow.
I want to add I don’t think that everyone is stupid. But the sheer silliness of the objections I’ve received so far are completely ridiculous. Every single one of the objections I’ve received were already verified by mathematicians. Some are just out there (like because a set has finite elements, that the set can’t be infinite, aka the finite path illusion).
e) If you think I’m autoposting is because I’ve already confirmed the results that people are objecting to by several mathematicians. Also, it’s only because the SAME issue always comes up.
“Diagonalization works because you can explicitly name a member which disproves the conjecture…”
Only for a subset of the list I give because the generator that Cantor uses to traverse my list is set up to only use said proper subset.
“I can see how you might think that being able to represent the reals as a tree is similar to representing them as an ordered list…”
No no no. My goodness. You see what you want to see. I’ve never said any such thing. Someone even asked me point blank. I said no. That’s not the way my argument is set up.
“The only way to show this is either with an explicit map, or by contradiction.”
No, and it’s arrogant of you to suggest such a thing. If a proof is valid, regardless of the method used, then it should stand on its own merits. I’m using the premise that if |N|>|R| and |R|>|N|, then |N|=|R|. I’ve mentioned this VERY CLEARLY several times.
Thanks for your suggestions Steve, but I can’t in good conscience follow them. I know you meant well, but it boils down to one thing. No one has any objections against my proof that haven’t already been invalidated by other mathematicians. They don’t like that I point out that they’re actually arguing against Cantor’s diagonal argument when they do this. But note that it’s VERY effective.
Mr X, not to beat about the bush, you’re not convincing me, and you don’t seem close to the point of changing your mind either. So instead of dwelling on the details of Cantor’s proof, or your claimed refutation of it, can I take advantage of your presence as an articulate ‘Count’, and enquire about some corollaries of your position?
How do you account for the fact that an error – and rather a trivial error according your posts above – has remained in the mathematical textbooks for a century, and continues to do so, despite the close attentions of many mathematicians? And despite, for that matter, no shortage of people drawing attention to the erroneous nature of the proof? NB I’m not asking this as an appeal to authority, but as a sociological question about mathematical culture, which presumably requires addressing with some urgency.
More widely – and feel free not to answer this personal question – are you something of a non-conformist across the board? Do you hold many other beliefs whose facts directly contradict received wisdom, in whatever scientific or historical field? Or is Cantor a particular bone of contention for you?
Richard Elwes: “How do you account for the fact that an error – and rather a trivial error according your posts above – has remained in the mathematical textbooks for a century, and continues to do so, despite the close attentions of many mathematicians?”
Because very few people understand the concept of infinity. Cantor himself took infinity to be a finite number. This is how he built Cantor’s diagonal. Go look yourself at the objections I’ve received so far. They are complete nonsense (at least the ones I’ve read so far before today). They’re saying that because each item is finite, that the path can’t be infinite. My goodness, all elements of N are finite, yet the list is infinite. Cantor’s diagonal only consists of finite digits, but do we see objections to that? Of course not. And you’ll find that mathematicians will respond in exactly these two different ways depending if they know it’s about Cantor’s proofs or not. You may not believe this, but I promise you it’s true. There is a defensiveness about Cantor’s proof that blocks the conversation. In fact, I doubt any mathematician even remotely thinks that Cantor can be wrong. So much so, that they’ll answer two different ways to the same question depending if you utter the name Cantor or not.
There’s not only that, but infinity the way that Cantor presents it in his diagonal proof is VERY clever (in a devious way). The inherent contradiction is a FEATURE of infinity, not a contradiction. Yes, you can normally map two countable sets one to one, but it’s not a requirement. So when Cantor creates his diagonal, he’s only mapping to a subset of N. So when I tell someone that he doesn’t go through every number, people respond “EXACTLY! It means that you could not put all numbers in the list.” See, the flaw is itself the result/contradiction that Cantor is looking for. How do you spot something like that when the rules for infinity are so crudely constructed that these two attributes of infinity cannot be clearly distinguished?
I’ll give you an example of these ambiguous notions. I still hear bona fide mathematicians say that the naturals in N don’t use infinite digits because every natural number uses finite digits. So they say something like it uses arbitrary digits. That’s pure nonsense. It’s either finite digits or infinite digits. The answer is simple. Finite naturals use finite digits, but infinite naturals use infinitely many digits.
I could go on and on about this and it appears I already have.
Short story is that I’ve given you only TWO examples of where mathematicians still get it wrong. I could list many more. Like the fact that you can’t have an infinite list without its generator and neither can you traverse a list without one (the closest I’ve heard a mathematician say about this is that order is important). Which generator does Cantor use when he traverses a list that you give him? Does he use the one you gave him? Of course not. He uses his own that only traverses a subset of N. Also, Cantor’s proof was rejected in the past. In fact, Cantor’s ideas have had a rough road. So your question is based on a false premise that’s it’s a fait accompli.
“More widely – and feel free not to answer this personal question – are you something of a non-conformist across the board?”
Only in a few specific areas of interest where I’ve done research. I did have a few ideas in another field that I work in professionally and ended up being correct about a few of those. They’re now widely accepted, but it was buried for a very long time. I was called far worse than a crackpot. Funny how time can flip the situation… much like Cantor (in reverse). While investigating other ideas, many of those are shot down early (and as it should be). That’s why the flaw in Cantor’s diagonal is interesting. It’s something I see that no one even bothers to want to look at. It’s no so much overlooked at it’s intentionally avoided.
I like to look at things from different angles. But no, I don’t waste my time being contentious if that’s what you’re asking. And no, I don’t have any other areas at the present where I’m rocking the boat so to speak. My ideas in my field are becoming more popular every day and that’s keeping my interest as more tools and applications show up.
Dear Richard,
“How do you account for the fact that an error – and rather a trivial error according your posts above – has remained in the mathematical textbooks for a century, and continues to do so, despite the close attentions of many mathematicians?” The last step of going to infinity has no justification in plain explanation given by Cantor. We can construct inverse proof, which will be valid to the last step, where Cantor tells that his constructed string is not in the list, whereas MrX says that it is in the list, we just did not check all strings. MrX says that you are just fooling me in that you can make the last step in the infinite list of strings. In MrX settings the last step would read – after each Cantor step there is exactly one infinitely countable subset of strings that contain substing of so far constructed Cantor sequence, therefore there is no step where Cantor sequence is excluded no matter how you constructed it QED.
Now, the math is a set of axioms, and whether to accept them or not is up to you. Accepting Cantor step (inventing axioms consistent with it), people got interesting math, and that is why it is in the text books. But there is no logical justification of Cantor last step within presented in Wikipedia proof.
And I do not here neither Gowers, nor Lipton, comments to the matter. MrX arguments is probably the closest to the confusion get by the students. Leaving that unexplained does not make a good job in popularizing science. Most of the comments are trying to attack MrX personally of not understanding the issue, whereas there is no “as clear as Cantor proof” explanations what is wrong. If many people do not understand it there are should be subtle issues involved. This may be a good place to cover them. After all what Kroneker did not like in the proof?
Bill Lawvere wrote a paper extracting the essence of the diagonal argument
http://www.tac.mta.ca/tac/reprints/articles/15/tr15abs.html
which works without reference to infinity, the collection of real numbers and natural numbers and so on. One point of category theory for me is to find the ‘actual’ proof, and drop all the cruft (mathematical and psychological) that hangs onto a problem. Theorem 1.1 in the paper is remarkably simple, and corollary 1.2 contains as a special case the result that no set surjects onto its power set. Once that is established, one only needs to show that the power set of the naturals is bijective with (0,1) (say) and hence the set of reals. The proof of theorem 1.1 can be carried out with very weak logic (one certainly doesn’t need set theory, let along talking about actual sets of real numbers), and so if one is of a constructive inclination, then the bijection |P(N)| = |R| might come under suspicion. But that is a different issue to doubting the diagonal argument.
I should say that Lawvere’s remark “Cantor’s theorem follows with Y = 2” should be applied to corollary 1.2 with the endomorphism 2 -> 2 swapping the two elements. It is this hypothesis that gives the non-existence of a surjection N -> P(N), not the nature of N.
The best posts on this topic (IMHO) have been those that provide good references, and the Lawvere reference that David Roberts provides is excellent. Yet in mathematics as in every other human endeavor it is neither necessary, nor feasible, nor even desirable that everyone think alike.
As an example we can point to the “anti-Lawvere” point-of-view that Doron Zeilberger expresses in his recent Opinion 108: … The feeling is mutual: I Feel Sorry for Infinitarian Hugh Woodin for Feeling Sorry for Finitists Like Myself! (And the “Lowly” Finite is MUCH more Beautiful than any “Infinite”).
It is natural to read both Lawvere and Zeilberger with enjoyment, which illustrates how pernicious is the doctrine — so thoroughly discredited by Gödel and his successors (including this weblog) — that mathematical truth can be captured by any one set of axioms, or that the pursuit of that truth requires only one style of human cognition.
Thank you, John!
I don’t mean to say that everyone should think of the diagonal argument a la Lawvere, but that it *can be done* without the baggage of the infinite (and in weak logic). I would invite Mr X to read the Lawvere paper (it may necessitate learning some new mathematics, always a good thing) if s/he pleases, and try to pick holes in it.
Thank you, David.
It seems to me that conflicting opinions relating to Cantor’s theorem (as seen on this thread for example) can be appreciated as being largely about conflicting notions of mathematical “naturality”, and (to my mind) the great attraction of Lawvere-style category-theoretic analyses is that naturality explicitly is central to their arguments.
And yet even the uncontentious notion of “naturality” means different things to different people. For many but not all folks, Zeilberger-style experimentation is a vital part of mathematics-as-cognitive-process, as contrasted with mathematics-as-theorem-proving. Thus, whenever I see a commutative or projective diagram, I like to ask “how can I test this diagram’s truth in some concrete practical context?” Needless to say, this is a reasonably effective heuristic for discovering new category-theoretic diagrams (the proof of a given diagram being often straightforward, in striking contrast to the difficulty of its conception).
The union of formal (category-theoretic) naturality with experimental (Zeilberger-style) naturality has an accepted name … it is what we broadly called “geometry” in its differential, algebraic, and dynamical aspects.
Thus, for me the unattractive aspect of Cantor’s Theorem (and other theorems in its class) is that these theorems are not about geometry (in any sense that I can readily appreciate that is).
To put it another way, if concrete geometric significance could be attached to Cantor’s Theorem, and other theorems relating to transfinite cardinalities, then the mathematical attractiveness of these theorems (for me) would redouble. 🙂
As always, this post is very interesting, thanks.
Related to MrX, please let’s be civilized as bowaggoner asked previously, being offensive will never make your point.
Moreover, your proof does not work for the simple reason that it needs R to be countable for this construction to work. I agree that you can theorically build such a tree, yet you do not have a working injection form N to R unless R is countable.
I will not go into detail into your obscure implicit construction of the injection (which you cannot give explicitely as it does not exists) but simply on one point:
“This means that the cardinality of all the paths is limited by the cardinality of all the nodes.”
Unfortunately you have an infinite number of numbers (the irrationnal numbers but also an infinite subset of rationnal or all of the rationnal depending on how you decide to represent those who finishes by an inifinite number of 0) whose number of nodes on their paths is infinite… So basically there is an infinite number of infinite number of nodes…
Just as Delta said:
“it means that the cardinality of all *finite* paths is limited by the cardinality of all the nodes.”
Therefore, in fact you only prove that the set of the numbers whose decimal expansion is finite (which is a subset of Q) is countable.
Moreover, if you want to go with a random path pickup, the probability of picking a precise path is 0 and even the probability of picking up a path of a number that is in any subset of R different from R is 0. Hence, you cannot build your injection that way.
Regards,
Michaël
Regarding the last paragraph about the probability what I said is accurate, I should correct it to :
Moreover, if you want to go with a random path pickup, the probability of picking a precise path is 0 and even the probability of picking up a path of a number that is in any finite union of closed intervals (hence excluding + or – the infinite and therefore different from R) of R is 0. Hence, you cannot build your injection that way.
Regards.
Mic: “Therefore, in fact you only prove that the set of the numbers whose decimal expansion is finite (which is a subset of Q) is countable.”
And Cantor only checks finite amounts of digits as well when constructing the diagonal. Your argument amounts to Cantor can only check finite length reals. The problem is that I never stop at any particular digit as is a requirement for me to check Q. I always check the next digit. Proof by contradiction for you.
> And Cantor only checks finite amounts of digits as well when constructing the diagonal.
No.
Hajduk: You miss the point. I’m not saying that. I’m stating what Mic’s argument means in the context of Cantor’s diagonal.
Maybe the result is that the issue of countability is undecided. Since the process never stops, the checking can never ocurr. But the process is also never expected to end, thus all irrationals would be missing.
The issue being what would happen if we consider infinite steps have happened, and PI is the list.
That would mean that numbers of infinite length (and sizes, or precision) are now included. Hoever, this would be larger than the naturals if we never allow them to reach N, featuring numbers with infinite digits. If there any such number, it eill no be natural nor computable. Which is the same exact case with PI. Since we can never draw a circle and it’s radium with infinite precision, nor have a way to exactly state that relation numerically, or list all digits, both this number or a “natural” with infinite digits are a little hard to comprehend, and the rules at this level MUST be so, that these numbers would be of a different nature than a finite number like 5 or 766666 or any other finite natural. You can’t add 1 to that infinite natural (no last digit), and youcannot add anything to the last decimal of PI, it’d do nothing. You can only operate in regions, just like in probability any given point means P is 0. So these infinite numbers only make sense in relation to other infinite number there, be it 1 in the Real 1-0 space, or another infinite number in the pseudo “natural” of infinite length. this pseudo natural would have the property exactly like an irrational: that addition only results in something if the other number is also non finite. And that if you define the largest number, that is arbitrary – there is no largest number, just like addiong 0.50000000… And 0.5000000… (Both w/infinite zeros to be fully described) would add to 1, but you can keep adding. So the real of infinite legth numbers is the result only of allowing infinite elements in a set, each of infinite precision or size, but that compared to other infinite legth numbers, they are always exactly smaller or larger to those other numbers.
At the end, the problem is that if you allow a number in N to (by virtue of allowing it to reach infinity) to have numbers of infinite length, all thise numbers would have no meaning in the Natural sense: add 1 and it’s the same number. 1 in that context amounts to a quantity infinitely small, essentially 0. And you don’t reach that by adding 1 to a finite number, no mayter how long you carry the process. Likewise, the same for an Irrational. However, we know the Irrational has a known meaning like PI or “e”. The problem is e or PI…ee’ll never know the digits, but ee can use their finite versions for anything, and can also use and manipulate them as labels in formulas. If N is allowed to reach infinity, like so the Rationals would include PI.
So all the discourse is that you can reach ANY natural by adding 1 so mant times (as none is supposedly allowed to become of infinite length). Likewise, you CAN’T reach the Decimal part of PI or e by starting at 0.1000…. (Infinite digits) and adding the smallest element in that set, one at a time.
So you either add numbers of Infinite length (aka Precision, as in all these cases the only make sense in relation to other infinite numbers ie. Proportionas of infinite precision) or you only add numbers that are finite.
One starts with the unit, and adds to it. The other starts with an arbitrary space filled with a definite but infinite amount of elements, lets say Reals between 0 and 1, and divide that infinity through cuts of infinite accuracy (any rational described with infinite precision ie. 0.333…) or Irrationals like PI. The Relas are this space, and since you can have 3.145… (Part that is “natural” and a decimal part), in this treatment, you can have natural-like part and an Irrational like part. But these natural parts are SuperNaturals, in that in any of these integers there’s infinitely many elements in them. And the SUM operation does never apply to those elements that compose them, but to sets eith infinite numbers of them (eg. 2/3 is the distribution of infinitely small elements, withe rule 2 in the set for every three if them, and allowing the rule to complete in infinite time).
Yet, the cardinality for me is still elusive (disregarding formal axioms of what it means, or irrespective to them) because one doesn’t know exactly what would happen if we were to witness N in its entirety, which must include F (all finites) and also other numbers as well (otherwise N would be a shorthand for whatever largest number you can imagine, and 0% of the “possible N”).
Do you trully allow infinite steps? Steps, imply time as something happens before and something after. In infinite time, nobody knows exactly how something finite becomes infinite. And thus for me, the “Cardinality” of N, R, or any other type of number, is elusive, as each has infinite steps of the same nature, but Reals are assured true infinite steps (infinite lenght quantities or digits), just to make sure PI is there.
[ You have understood that the not before accurate is missing 😉 ]
Don`t care about the models that much. Seriously. Model theory didn`t turn out to be what was hoped. You can`t formalize the interpretation of your _fundamental theory_. You need to have some starting point. The intuitive natural interpretation we give to, say, ZFC is all what we got.
If you start doing model theory and try to make ultimate sense of your fundamental theory you meet uncountable models and countable models, all kinds of crazy interpretations etc. It makes sense because model theory takes account of all possible interpretations of your theory and some of them are crazy. If you use second order logic you still need to decide what semantics you use. For me all possible interpretations semantics is the true standard semantics. Full semantics looks some kind of scam to me:) Or it`s understood wrongly.
We are just talking about principles what we use. Math can`t decide this. The power set axiom together with infinity tells us that uncountable set`s exist. If you don`t like it let the former go. The is no proof after that.
For me the trouble was that some infinities were “bigger” than others, which seemed really crazy. But IMO it`s just that bigger means different thing with respect to infinities than finite things. A proper subset of an finite set is smaller, period. This doesn`t hold in the infinite case. We have a same definition of cardinality which is enough to deal the both case. But in the infinite case the consept of set size still feels different, it doens`t have the familiar consequences. IMHO it`s just not exactly the same consept.
I am by no means qualified to add anything meaningful to this debate. I can follow Cantor’s diagonalization argument, and see no obvious flaws with it. I follow the general idea of MrX’s argument, but am not exactly sure how to fill in some of the gaps, or justify the required assertions, that others have already repeatedly inquired about. Perhaps it is indeed the case that most of us simply don’t understand infinity, although I am not sure why this means that it is more appropriate for MrX to ridicule us than to give a rigorous explanation about why the objections to his argument are incorrect.
However, I do wholeheartedly agree with his sentiment that it would be wonderful if Lipton, or Gowers, or some other mathematical genius, would come to the rescue and articulate what — if anything — is wrong with his argument. As it stands, MrX insists that we are all to dumb to understand, but that many brilliant anonymous mathematicians have already been fooled into confirming each of his claims, from which he believes it follows that his argument is correct and Cantor’s is bogus. The debate will not move forward until some other mathematician who is simply “too smart” to be written off as “too dumb” gives his or her own two cents on the argument.
Perhaps MrX is correct, and perhaps he is wrong. There is no way for us mere mortals to know until MrX writes up a very careful formal proof, or a genius comes along with an argument that refutes it (and explains why the argument doesn’t simply prove that they are just too stupid to fill in the missing pieces that would turn MrX’s intuition into a proof).
Dear Prof. Lipton,
I wouldn’t call Skolem’s paradox “a fundamental reason to doubt Cantor’s proof”. In a countable model of ZFC, there’s still no set representing a bijection between the naturals and the reals. Inside any model of ZFC the provable cardinalities are the same, even when from the outside everything is countable.
I’m an UnCount. Still, sometimes I wonder, does Cantor’s proof need modifications if we begin with “Suppose the onto function r: R → N exists, but is uncomputable”?
Using the Wiki reference:
http://en.wikipedia.org/wiki/Cantor%27s_diagonal_argument#An_uncountable_set
If I cannot compute the nth element in the nth sequence, I cannot construct the new sequence that is different from the enumerated sequences.
I know it shouldn’t matter, all I need is existence, not computability. Yet I wonder.
huh? you don’t need computability.
however, if you’re curious, consider that:
if such a function exists, then a computable such function exists.
namely, if they are countable, then any simple enumeration has the property that we need. so the straightforward enumeration would be such a function. (in binary, write down all 1-digit reals, all 2-digit reals, and so on). you can restrict yourself to the interval [0,1] if it is easier to think about.
PS: onto isn’t enough.
s.
Sorry, I transposed N & R. Starting over, suppose the onto function r:N->R exists but is uncomputable?
—
Regarding the substance of your comment – I thought that it is a true result that not all functions from the integers to the integers is computable. So this postulated function r from integers to reals could be uncomputable. All the diagonal argument proves then is that this r is indeed uncomputable.
If you allow counting rations with a different devise, like Cantor does with the Rationals – a rule that goes through all of them – then that suffices.
The Reals are just Rationals plus Irrationals. The binary tree by MrX is just another way to map all of what is called the Rationals – in a sense that we can understand a process to infinity that would never require numbers (numerator or denominator) each of infinite lenght in both what each represent as a quantity or in notation.
When we move to the Reals, we know there are numbers like (PI – 3), and irrational component. We know they are a very specific relation that requires infinite digits to be represented by our numeric devices to represent the computation.
Because rationals are actually divisions, we can write all of them as divisions, each describing the operation and quantities in each row/column (Cantor’s arrangement). They can also be represented as decimals. But these decimals (arising from Finite rationals) do no represent include (PI – 3) or (e – 2), irrationals.
So when MrX does a tree (an equivalent thing to the matrix arrangement of the Rationals by Cantor), which also happens to be include the DECIMAL matrix Cantor uses for Reals, he seems to be saying that since (for eg.) representing 0.33333… Also requires infinite steps, a ratio, and he uses the same technique a Cantor for decimals, then his process maps EVERY DIGIT … Eventually (the process never stops and all numbers are given proper care), then if you argue that 1/3 can’t be covered, then Rationals are uncountable. But since Cantor showed they are, then 0.3333… Is indeed accounted eventually (with infinite time to carry the process), and thus (PI – 3) has to be accounted too, since it’s solely composed of digits and he accounts for any and all possible digits.
Either Rationals are uncountable, along with Reals, or both are none. And they have the same cardinaly.
This seems mostly tha most Countables intuitively, one way or another, think.
However, the Uncountables usually know they axioms and things they presupose very well, as any gradutae will 99% agree with the Cantor proof, seems to see that 1/3 LEADS to an infinite lenght representation with 1/3 not requiring any digit. It’s 1/3 period. But (PI – 3) or any irrational is PROVEN TO NOT BE A RATIONAL. And even if Cantor’s bogus matrix is not being used to prove what Cantor think he is proving (that of “larger infinities”), they all agree there is no one to one mapping of Naturals (1, 2, 3, …) to map one to one because MrX mapping is just rationals at the end, which will exclude irrationals, and thus, can agree with Cantor, even if nobody knows exactly what the larger infinity actually is, if anything other that the mapping doesn’t seems possible.
My view is that the naturals are a way to Multiply 1 to infinity. The rationals are a way to divide 1 into infinite piecez. And that by the rules and axioms set up in Rationals, you don’t get into numerators and enumerators of infinite lenght… Limits are a devise to think and reach conclusions as you approach infinity, but infinity is never reached – only abstracted.
But presented by an Irrational, no limit or extrapolation can help you. When we want to specify (PI – 3) numerically and not by label, we either give out the operation (Perimiter / radius / 2) or show the first digits of what we know is an infinite number of digits.
This forces considering the range (0,1) of Reals as represented by infinitely small Rocks (a kind of small unit). Instead of a process, the irrationals require infinite precision in the ratios they represent, and no finite rational can account for them.
In essence, the Irrationals have bridged the gap between the small unit (A Rock, infinitely small unit) and 1, which represents the area of all Rocks, each infinitely small.
If you add each Rock, one by one, you never reach 1. That is, under the rules of a natural number, what’s still left to be enumerated ipractically always add us to 100% of the larger 1 (infinity). With the Rationals, same thing happens IF when make clear they aren’t allowed to be numbers (ratios) of infinite numerators and denominators (which is think is the notmal rule). By definition, MrX is not allowed to reach (PI – 3) ever. If he lets his tree grow Forever, and someone witnesses the result, he has infinite numbers of infinite legnth each, which upsets him if disallowed, asking either to be allowed the same rules Cantor is allowed, or disallowing both.
So all of the people upset at both sides are really awarely trying to explain Reals are allowed to have numbers of infinite legths, and Naturals are not. And MrX or other Countables, are explaining that if that different treatment is removed, there’s no way a regenerator or rule like that of Cantor’s Rationals or MrX nodes to cover all the digit space that also occupies (PI -3).
My view I stated, if you have a process like adding units to 1 (or 0), or dividing 1, they have the same cardinality obviously. And each, by rules of construction are composed of finite precision (there’s always a larger number, or Of a more precise “cut” or division implyng a larger number of Rocks). But when we encounter PI, our rules for Rationals exclude it, because accepting (PI – 3) is accepting you need infinite precision in the cut. And if (PI – 3) divides a pie in two, and you think of that number as the number of elements between 0 and 0.1428… And then 0.1428… And 1, each of those units is 0% of the total 1, because the cut results in infinite rocks ON EACH SIDE OF THE PIE. So in that sense, allowing infinite precision cuts (or divisions or real of infinite decimals) is a jump from 1 (The sum of infinite elements only making sense when operation on ranges, not a sum a units) into the smallest infinitely small units that I labeled Rocks.
And the real divide between MrX or equivalents, is that always the jump from finite to infinite. Is it a multithreaded thing? Where is the jump? What happens after we say “I continue this forever”? You can by definition frame this with franeworks, definitions, axioms, and reach conclusions – and assume those with other implicit views are dumb or don’t get you. If MrX is allowed to carrie his experiment Forever, and some being can deal with infinity, will he/she find (PI – 3) in after the process and instructions he setup? Can his process complete in infinite time? If by definition it can’t, (PI – 3) will not be there (or there yet, or there Ever). And it must be by serup, because that neverending process that never ends is assumed to either complete or never to. And if so, the same should apply to Naturals and Rationals. And if such, Cantor has just defined Reals as the exclusive domains of those numbers that are allowed to eventually complete and people accepted that definition, yet we know that we’ll never know the true amount that (PI -3) is, as the best we can do is continue our life by either using the irrational simbol, or pragmatically using a good enough digit approximation.
Ultimately, the Real is the acceptance that a process resulting in Rationals of finite length misses Irrationals, and that there exists such thing as a 1 divided into infinitely small pieces or Rocks, and that you can make infinite subgroups each of infinite number of elements, at every point, can be divided into two groups (say PI – 3 represents a cut a long a pie at the 0.14… position) each with an infinite amount of elements, but one being larger than the other, just because when you account for all Rocks relative to the other, one has 0.14… Of the total Pie, and the other side has 1 – 0.14… of it. And any cut, of which there are infinite cuts, gets you groups and subgroups of infinite elements (by fact that PI – 3 requires infinite digits or precision in the cut, just like any other irrational) each.
Yet, relax that MrX is now allowed to make his tree operate in infinite time. And the resolution, number of nodes will be infinite. Now there are infinite number of numbers each of infinite length. And PI – 3 is covered. So the cardinality of N and R is the same. If you disallow him that, clarify that he is not allowed by Definition to continue Forever (tree and each number never become infinite in size and length), and what allowing the process to do that might mean. It might mean for those pointing him his “error”, that what MrX is doing is stating a Rational is now a Real (his definition of what can happen is everybody elses definition of a Real, and all and him are reaching a similar conclusion and calling it different outcomes) or that maybe there aren’t different “cardinalities”, but that somehow, it’s semantic: things not allowed to actually use infinite time, came to be called of certain cardinality, and those allowed to do so, of a larger cardinality. And these cardinalities thus are just labels for what’s allowed here and there, and have nothing to do with the true size of infinity: something not allowed to have number of infinite length at some piint in eternity, will obviously ALWAYS (by definition) be missing numbers. Even if you say Forever, it’s always in process and 0% complete.
The fact remains, we don’t know where the “jump” occurs, except in our imagination, in thinking that given a radius, you can draw a precise Line representing a perimiter (which is imposible in the precise sense for us).
“unfortunately, we live in a world where the irrationals are uncountable”
Dear MrX,
I’ll try to reach you, by presenting the diagonal theorem in a more general way. There will be no mention of real numbers, natural numbers, or even whether the sets involved are finite or infinite. All it uses, are the axioms and inference rules of set theory (except the axiom of infinity, which will not be used here). I’ll also avoid “proof by contradiction”. If you follow this carefully, you’ll find the proof is irrefutable.
Definition: Powerset(X) = set of all subsets of X
Diagonal Theorem: For any set X, for any function f: X –> Powerset(X), there is some S in Powerset(X) such that: for no x in X is f(x) = S.
Proof: Let S = {set of all x in X, such that x not in f(x)}. I need to show that for every x in X, f(x) (not =) S.
Let x be any element of X. Then f(x) either contains x, or it doesn’t.
In the first case (f(x) contains x), we have x in f(x), thus x not in S (by definition of S). Since f(x) contains x, and S doesn’t contain x, we conclude f(x) (not =) S.
In the second case (f(x) doesn’t contain x) we have x not in f(x), thus x in S (by definition of S). Since S contains x and f(x) doesn’t contain x, we conclude f(x) (not =) S.
So in either case f(x) (not =) S. Since x could be any element of X, we have shown that for every x in X, f(x) (not =) S. The theorem is proved.
Okay, that theorem is proved. But what does that have to do with natural numbers and real numbers?
First, I’ll cook up a one-to-on correspondence, between (a subset of) the real numbers and Powerset(natural numbers). I’ll use {1, 2, 3,…} for the natural numbers. For some subset X of the natural numbers, the corresponding real number will be:
.(X1)(X2)(X3)… (base 3 expansion),
where for n = 1, 2, 3…:
Xn = 0, if N is not in X;
Xn = 2, if N is in X.
This puts Powerset(natural numbers) in 1-1 correspondence with a subset (called the Cantor set, after the very same Georg Cantor) of the real numbers.
Next, take any function f: (natural numbers) –> (Cantor set). Using the 1-1 correspondence, we can convert this to a map F: (natural numbers) –> Powerset(natural numbers). By the diagonal theorem, there is S in Powerset(natural numbers) which is not F(n) for any natural number n. Therefore, for the real number x corresponding to S: x is in the Cantor set, but x is not f(n) for any natural number n.
I think your 1-1 correspondence is none, because the sets {2,3,4,5,…} and {1} will map to the same real 1/3 (although they map to different string representations). Imho the construction can be saved if one chooses Xn=1 instead of Xn=2.
{1} corresponds to .2000000….(base 3) = 2/3, while {2, 3, 4, 5,…} corresponds to .022222…(base 3) = .100000…(base 3) = 1/3.
The point of using the Cantor set, is to separate this case and similar ones with an empty gap.
The reply depth seems to be bounded 😉
You’re right, I got it wrong, an elegant idea to avoid multiple representations!
George Kangas: It isn’t irrefutable at all. You don’t even mention what generators you use for x or f(x).
“I need to show that for every x in X…”
What generator is this? How are you going through every x? You cannot iterate through an infinite list (even N) without a generator. How are you choosing each successive x?
You haven’t proven anything at all. You can’t even get beyond one of the very first steps of your proof. And it’s SUCH a basic concept that anyone will tell you order is important in infinite sets. To completely disregard any notion of this is ridiculous. Heck, you don’t even mention by what criteria an element is IN f(x) or S or not. How do you do your matching? I can use your argument where the elements are using base 3 representations, but where I use a generator typically used by base 2 and you’ll NEVER go through all elements. And I can prove to you that this is exactly what you doing (with different bases) since you mention at the bottom what traversal algorithm you are using. I can guarantee you that it’s impossible to “show that for x in X” anything.
Your proof is so full of holes, it may as well be swiss cheese. There isn’t ONE single statement about how you deal with infinite lists. Not one.
You go through f(x)’s and you also go through x’s. Prove that you are using the same generator (same traversal process) for both and then we’ll talk. And don’t just say “sequential”. That means NOTHING with infinite lists. What is different between the current element and the next that makes you go from one to the next. Do you have them labeled? If so, how? What is f exactly that can make it select a portion of x? How does it do this? What specifically is different between each successive label? Does this impact the generator of x?
NONE of this is specified and you’re saying it’s irrefutable?
I’ll give you an example where you’d run into problems. I will have two lists. One is in base 2, the other is in base 3. Natural numbers in both. I go through base 2 list as you’d expect. In base 3, I use the exact same generator that I used is base 2 where I skip to the next number that matches the next successive base 2 representation. Am I using a one to one mapping? Yes and no. Between base 2 and those elements in base 3 that don’t use the digit 2, yes. But between both entire sets, no. The irony is that I’ve just mapped N to a proper subset of N. Cantor does exactly that with his traversal. He uses a generator normally reserved for listings where you have as many digits as the row count. You can use each generator in each list just fine, but when Cantor and yourself use the restricted generator on a list normally traversed with a base 2 generator, you cannot possibly traverse all elements any more than you can traverse a base 3 list using a base 2 list. And before you say that you don’t mention what generator you use in your proof, that’s the problem. But here’s the thing. You DO mention what traversal f(x) uses. And if you list X in a manner that works with that same generator, your proof fails because you will obtain a new element that cannot be represented in your list. Not because it’s a new number, but because it’d be like finding a base 3 number and trying to add it to a list represented in base 2.
Got it?
Sorry for the long post. But I just wanted to be clear since you mentioned this was an irrefutable proof.
Mr X,
You keep saying things like this:
You don’t even mention what generators you use for x or f(x).
Clearly “generators” are the key to your disbelief.
But here’s the thing – neither the standard presentation of Cantor’s diagonal argument, nor George Kangas’ very lucid argument above require any discussion whatsoever of “generators”. Despite your protestations, this is simply not a standard concept in elementary set theory. We have sets, and functions between sets, and that is basically all we need (and neither require “generators” in order to exist).
So, without lecturing me about how utterly basic and trivial it is, can you please define what it means to say “A is a generator of B”?
In infinite lists, the order is important. Not just when you generate the numbers, but also when you traverse them because you are effectively generating a certain sequence to be able to go to the next element. But not all generators are equal. You can traverse N using a generator that will only allow you to “reach” a subset of N. This is a well known principle that makes proper subsets possible. Without such generators, the mapping would be impossible. Generators are well known. Dedekind cuts and Peano axioms are common ones. It’s a well established property of infinite sets.
So when I hear things like “all x in f(x)” when talking about infinite sets, I cringe at how bad this is. It doesn’t mean a thing. How are you sequencing x? What is the ordering? What constitute the next item in the list? Is f(x) a set? If so, do they have a relationship to “all x” that would change said traversal? For example, Cantor’s diagonal can only reach a subset of N. Forget trying R or even N.
Just as an example, take two sets of N, A and B. A is listed in base 2 and B is listed in base 3. Now using a base 2 generator to traverse A while matching digits and you’ll reach N. But use the same generator on B and you’ll only reach a subset. What’s more important than this though is that even if you don’t match by digits (IOW, you don’t skip over elements), you will still traverse a subset of B. Cantor’s diagonal isn’t even base 2, it’s some restricted form of it.
> So when I hear things like “all x in f(x)” when talking about infinite sets, I cringe at how bad this is. It doesn’t mean a thing.
I just searched for “all x in f(x)” on this page, and the only hit is your comment.
Incidentally Mr X, thank you for your reply above. I hadn’t spotted it when I wrote that last comment. (These nested threads can become confusing.)
Dear MrX,
Thanks for reading my post, and replying at length.
I have studied traditional set theory (Zermelo Frankel set theory, or ZF), and never come across a thing called a generator. ZF requires no such concept for its treatment of infinite sets. That’s why my presentation of the diagonal theorem, while never mentioning infinite sets, nonetheless fully applies to infinite sets.
The proof (from the ZF axioms) that the reals are uncountable is just way too simple to be wrong. There’s no room for doubt about this: **IF** the ZF axioms are true, **THEN** the reals are uncountable. But wait… what if the ZF axioms AREN’T true? Well, then maybe you COULD count those reals.
You seem to believe that infinite sets require more special treatment (e.g., “generators”) than Zermelo and Frankel saw fit to provide. Okay then, you don’t believe ZF is a consistent theory. And if (as you believe) the reals are countable, then ZF is definitely NOT a consistent theory.
So, all you need to do is EXHIBIT FOR US this mapping from the natural numbers onto the real numbers, and you will instantly attain mathematical immortality. Z and F will tumble from their pedestals, giving way to your set theory.
Bear in mind, you will have to specify for us the COMPLETED mapping, let’s name it X, from the naturals onto the reals. Once it has been specified, YOU DON’T GET TO CHANGE IT ANYMORE!. We will then try to construct a real number which:
1) has a different digit in position 1, than your X(1);
2) has a different digit in position 2, than your X(2);
3)…4)… ad infinitum.
Please MrX, JUST SHOW US your mapping!
“You seem to believe that infinite sets require more special treatment (e.g., “generators”) than Zermelo and Frankel saw fit to provide.”
No. Peano axioms and Dedekind cuts are well known generators. Go look at Cantor’s generator. At how he traverses the list of reals. He can only get to a subset of N.
“Once it has been specified, YOU DON’T GET TO CHANGE IT ANYMORE!”
And yet you go and change the generator used to traverse said list. How quaint.
An infinite list is useless without its traversal algorithm. The traversal you mentioned is different than what I would give you. So your “proof” is flawed.
The mapping
, inverse representation of binary number, e.g. 
etc.
Cantor number: 0.0011111….1111….= 0.01= f(2)
@MrY: This is a mapping from N to Q, not from N to R. So e/4 is not contained in the image of your proposed f.
Can you prove that?
Yes, all numbers in the image of your function are rational numbers (since they have only a finite number of digits, at least as you wrote it down). e is known to be no rational number, hence e/4 is no rational number.
OK, if you say. Than leave f(1) and f(2) intact, and then fill the rest of the infinite^2 table with random binary numbers (p=1/2). Once completed put zeros on the diagonal starting from the third term and remove repeated sequences.
then for any real number its corresponding sequences are in the list. Testing from the first to the last (infinite) digit: there is always a subset that contains initial digits which is twice smaller than left from previous digit, but still infinite. Since there is no step excluding the number it is in the original set. Therefore, all real numbers are present.
Constructing Cantor number gives f(2).
Then f(3), f(4), f(5) will not be in your enumeration, except you fill the rest with “random zeros”. Then we have the same problem as above. Btw. don’t mix up (finite or infinite) binary strings with real numbers, there is no one-to-one correspondence between them.
http://en.wikipedia.org/wiki/Cantor's_diagonal_argument gives bijection that excludes previous f(3), f(4), f(5)
Mr X,
The problem is your are so fixated with people traversing infinite lists armed with some generator that you didn’t bother to read what George Kangas wrote.
Read his proof again, leaving all that baggage behind. There are no lists involved, only sets. It is not even assumed that the set X is ordered. There are no generators. No-one traverses anything. All of these concepts are utterly irrelevant.
His proof starts with a set X (whether finite or infinite, ordered or unordered), and a function f (whether generated or ungenerated, traversable or not) from X to its powerset. And then he proves in a lovely direct way that f is not surjective. And that’s it!
Richard Elwes: There is an assumed ordering (that’s the whole point) and he changes that ordering in his “proof” leading to a bogus contradiction. You can’t just traverse each subset and then say you’re not.
No, Mr X, you are mistaken. No ordering is required, mentioned, or assumed.
I’m talking about the proof presented in the first half of George Kangas’ comment here.
In fact, that argument posits no conditions on the set X whatsoever. And nor does anyone need to “traverse” any subsets, whatever this may mean.
That theorem (aka Cantor’s theorem) says that no set can be mapped surjectively onto its powerset. And if you disagree with that, then I think it’s about time you produced a counterexample.
MrX, you seem to take it as an article of faith that all infinite sets have an implicit “traversal algorithm” which allows you to enumerate their elements… so it is an axiom of your very non-standard theory that all infinite sets are countable. Given that, it’s trivial to prove that all infinite sets are countable, because you’ve defined them so! However, your “theory” is irreconcilable with standard set theory, as Cantor’s theorem shows. It’s also clear that whatever your notion of a “set” is, it does not encompass the real numbers.
pelotom: “MrX, you seem to take it as an article of faith that all infinite sets have an implicit “traversal algorithm””
What I’m saying is that the WAY you use the axiom of choice will define the proper subset that you are selecting into. This is the whole reason why we have the question of one to one mappings. Different mappings create different selection based on this mappingh. When you have a mapping, you can select the item in the first set (because it has a predefined traversal) to obtain the element in the second. What you’re trying to say is that such a mapping is irrelevant. We can select what we want at random, yet we’re trying to prove that such a mapping is possible or not. Your argument is nothing more than an assertion to use circular arguments. To leave in an inherent contradiction just to obtain a result that you’ve been taught to believe.
Remember, if what you say is true, then Cantor’s diagonal is unnecessary. No such mapping is required. Just announce what you believe to be true and be done with it.
The biggest issue I see is that mathematicians don’t believe that one to one mappings exist when they are using one. It’s truly baffling how they select into an infinite set without defining what proper subset they are using. All proper subsets are equivalent. If you don’t define which one you are using, you have a self imposed contradiction.
Guys you are converting me to Count :(.
@George Kangas: take map f(x) that S is empty set, i.e. all natural numbers are in the image of f. Then constructing real numbers from PowerSet the S would correspond to 0, which does not have to be represented, since we need representation of open interval.
It seems that “Uncount” is convenient construction/approximation, that does not have any real world counterpart like vacuum, Newtonian mechanics and homogeneous media, but still good enough at representing reality.
Yes, because at first sight the real world actually *looks* indivisible and infinite – due in fact to the imperfection of our senses. Democritus’ hypothesis of atoms was a very daring claim at his time, while it took no less than Archimedes to state that no quantity was too large to be counted.
Sorry, I meant “infinitely divisible and infinite”. 🙂
It’s our knowledge of the discontinuities of matter – elementary particles – and of the finiteness of the universe – Big Bang theory – that has made some scientists feel otherwise. Science told us that infinite collections didn’t exist and in return, some mathematicians have become unable to even imagine them. But initially, Cantor’s infinite sets were the result of a long tradition of viewing the world as fundamentally continuous and infinite.
Suppose we don’t want to use those arguments. Just the definition of a decimal (or binary) number, natural numbers and the concept of allowing a process to continue forever, and finishing.
Take any Irrational, and think of it as a specific number (or proportion more precisely) that must be represented somehow, and we decide to use decimals or base 2.
MrX shows a way, or process that is linear, that starts generating the equivalent of ANY number represented by digits. At an advanced stage it would feature the first (lets say) the first the digits of ANY REAL. At a later stage, maybe the first 10^500 first digits of ANY REAL. The process once started is never changed, adapted, flipped or modified in any way. At any moment in finite time, he has covered 0% of the infinite numbers in N, and between any two IRRATIONALS, the gaps are narrowing, but there’s still and infinite amount of digits to be produced.
The ultimate question here, if you’d agree MrX is doing what I just summarized, is this: at any point in time, there’s still an infinite amount of naturals left to use, and an infinite amount of new digits to be produced. But at every point, he has used more steps, and is covering the entire set of Reals up to a certain number of digits.
Then it follows that he will never run out of naturals numbers, and he will never run out of new digits to produce to accurately portray each Real.
In that sense, the mapping can continue forever, never exhausting any set.
The only way to probe the Cardinality of N is smaller than that of the Reals (0-1) is to show he will run out of natural numbers before he runs out of digits of rationals to detail.
Hiwever, we know a rational implies infinite precision. And that we need to allow infinite number of steps to get to PI.
If he is allowed infinite steps, the each tree will be of infinite legth, and every Real should be there listed. You’d be seeing the infinite number of Reals, each with infinite digits (remember, 0.1 is a shorthand for 0.10000… And 0.333… Is a shorthand just like PI is a shorthand for 0.145(etc)).
But if you don’t allow infinite number of steps to be completed, you’d be asking if a finite set is a subgroup of an infinite set. If Cantor wanted to prove that, he wouldn’t have need a diagonal at all, so that’s not what he was trying to say).
If you allow him to complete the infinite steps required, every number is there. Tou can logically created a diagonal, and your resulting element will not be a finite element. It will be the equivalent of saying INFINiTE + 1. Think it another way, you have every Real, including the decimal part of PI. What is the “last” element of that number that you want to flip? There are infinite number of digits, and there’sq NO last digit. How can you flip it? Or think of PI as dividing a pie composed of infinitely many atoms, and that decimal part of PI divides those into a group with 14.528…% of them, the other group with the remainder. Each set has infinitely many elements. Each element, at this infinitely small size of atoms, weights 0. What is the impact of flipping the last digit (if it ever had one which it does not)? Zero. It’s like adding one to infinity. You cannot construct a new number in this set, and it being one not already included.
That last part is not necessary to explain what I mean. It’s there to express my thought as to why Cantor cannot use an infinite list, and treat it as finite. Cant tKe a finite list and fine new elements as if it where any news. And even if he could take an infinite list and get to the last digit, and then was able to change that last digit (or any digit adjacent to the “last” digit of this infinite sequence of digits and flip that one, even then, that would amount to no change to it.
Hi, Preemption,
Wow! This comment thread just won’t die!
The reason I tried to sell MrX the diagonal argument as pure set theory, instead of some elaborate procedure involving decimal or binary digit strings, was to present the argument in its simplest, clearest form. MrX’s informal arguments, laced as they were with hand-wavy assertions about the nature of infinite strings and infinite processes, introduced layers of complication and confusion.
If you don’t want to go all the way to formal set theory, you can still strip away a lot of confusion just by dispensing with time and processes.
Take any enumeration of reals, and imagine it in its “published” form: a FOREVER UNCHANGING infinity-by-infinity array of bits (binary digits), printed out on infinity-by-infinity paper. That array has a diagonal which never changes, and that diagonal has a complement (bit flip) which never changes. Because that diagonal complement is non-identical to EVERY ROW of the infinity-by-infinity array, we know that the array (and the enumeration it represents) is incomplete.
Because EVERY enumeration has a diagonal complement, EVERY enumeration is incomplete!
@George: Why use that one particular well known mapping from all the mappings that are possible? It’s well known to not be one to one. Nothing you put in that grid will give a one to one relationship, even N. So why use it? The only representation that is 1 to 1 in a grid is the identity matrix (DUH). It’s silly to expect any different result. Cantor’s result holds true of N as well. But we know that N can clearly map to N. So if the proof doesn’t hold up for N, what good is it for R?
And if you come back with a response about inverting digits, then it’ll be clear you don’t understand the topic. The diagonal isn’t the point, but rather that it can be shown that the diagonal doesn’t reach all rows.
Hello again, MrX! I hope all is well with you.
You asked: “Why use that one particular mapping…”
What I said was: “take ANY enumeration [i.e., mapping from N] of reals…” So no, I never restricted myself to any particular mapping. Everything I said will be true of ALL mappings, as I point out in the final paragraph.
“The only representation that is 1 to 1 in a grid is the identity matrix (DUH).”
(HUH?) The mapping which matrix A represents is 1-1, if no two rows of A are identical.
An input to that mapping, is some row index i (a natural number). The corresponding output, is row i from the matrix A (interpreted as a real number). 1-1 is only violated when different inputs produce the same output, which never happens as long as no two rows are identical. So it does NOT require the identity matrix, to represent a 1-1 function.
Not that it even matters, whether the map is 1-1. We only care whether it’s ONTO. The purpose of the proof is show that it can’t be onto.
“Cantor’s result holds true of N as well.”
We’ve been over this, MrX. Yes, you can fill in a matrix, so that it represents some enumeration of N. You can take the complement of its diagonal. But that diagonal complement will not represent any natural number, because it will not be finite. All finite numbers have a leftmost (i.e., most significant) nonzero digit, but the diagonal complement has (at least some) nonzero digits all the infinite way leftward. So no, the proof does not work for N.
“…it can be shown, that the diagonal doesn’t reach all the rows.”
Let (i, j) = (position where row i intersects column j). Then the diagonal intersects row 1 at (1,1). It intersects row 2 at (2,2). And so forth! For ANY row: call its index i, then IT DOES intersect the diagonal, at position (i, i).
@George: I just said if you talk about flipping bits, then you don’t understand the topic. I even explained why. And what do you do? You come back and talk about flipping bits. You clearly don’t understand the purpose of the diagonal. Then you go on about natural numbers being finite. WOW! Talk about switching the conversation! At no point does that matter in this case. And the hilarious part is taking a specific order of digits in a natural number. Too bad. You don’t get to decide that. It’s hilarious that you would try to dictate that. If I want to cerate a diagonal in the other direction, you can’t stop me.
And the identity matrix IS the only input that is 1-1. You say it can be ONTO. Fine, but all enumerations are on the wrong side of the diagonal. So it’s not even wrong.
Also, an enumeration is NOT a mapping. The mapping is between digits and rows. This ONE particular mapping between digits and rows is NEVER 1-1 except for the identity matrix. This is trivially obvious that only one row is associated with one digit with the identity matrix. No other input makes this possible.
BTW, you go back to two rows not being identical. You can’t prove that with the diagonal because you never reach all rows because only the identity matrix will ever allow the digits to reach all rows. So you build a system known to not have all rows (IOW, use any other representation than the identity matrix) and then show there are rows missing. Big whoop.
Your other assumption is that digits and rows can be mapped 1-1 in that grid for N. It cannot. The same conclusion for R is true of N. You can’t reach all rows with the diagonal in both cases. You’ve just jumped to the wrong conclusion is all. Instead, assume that |R| = |N|. What would Cantor’s result mean in such a case? It would mean exactly what I’ve said. That the Cantor result is also true of N and that it only means that the mapping between digits and its rows is never 1-1 except for the identity matrix. There is NOTHING you’ve shown that makes one conclusion more worthy than the other. However, it’s trivially obvious that the identity matrix is the ONLY 1-1 input to the grid. This makes Cantor trivially wrong.
100% of what you’ve said is either wrong or not even wrong.
“100% of what you’ve said is either wrong or not even wrong.”
You’ve just described your own unfortunate situation, MrX. The good news, is that Cantor’s proof is actually far simpler than your ingeniously confused verbiage would imply. With a bit of humility, you could come at it afresh and just see how obvious it is. If interested, email me.
@George: You believe an enumeration is a mapping. Hard to discuss anything with that level of understanding. Just saying.
MrX,
Glad to see you are alive and well and still engaged in the problem of the diagonal.
Here is an observation which you may or may not find amusing.
If you flips all the bits on the identity matrix, then you have the adjacency list for a clique. Every element of the clique is 0 lines away from itself and 1 line away from every other element.
When you flip all the bits back to the identity matrix, then the diagonal represents one part of the total number of elements with 0 elements on all the shortest paths between and not including any two 1 parts.
As far as I can tell, the symmetry of flipping all the bits has nothing to do your argument.
I have been reading Brian Greene’s “The Elegant Universe” and trying to figure out why Super String Theory looks like Graph Theory on steroids.
@Jim: Not sure what cliques have to do with this, but yes, it is a restricted representation compared to straight binary. Since there is only a single non-zero digit allowed per row, then yeah, it’s always 2 digits difference from any other row.
Flipping the bits has never been the central part of Cantor’s proof. The diagonal is supposed to reach all rows (it doesn’t, but that’s the assumption because Cantor is incorrectly claiming to not be using his own custom non 1-1 mapping) and then you need to find a way where you prove it doesn’t. Circular argument to be sure. But the method that you use to prove that the diagonal doesn’t reach all rows is irrelevant as long as it works. Cantor flips bits. But it’s unnecessary. The only enumeration that is 1-1 with its digits is the identity matrix. It’s trivially true because it’s the only enumeration where you can prove that the only digits that are different between sequential rows is sequential digits. That’s the definition of 1-1. Flipping bits doesn’t adhere to the definition of 1-1. But the diagonal itself does… but as you can trivially see, the diagonal maps 1-1 to the identity matrix. But then I’m just repeating myself.
People often miss what Cantor was going after. They get stuck on the flipping of the digits. When I create a diagonal with N, I don’t need to flip bits to see it isn’t 1-1. I just need to see if the length (the position of the last non-zero digit) of each row is one more than the last row. If it isn’t, it isn’t 1-1 with the digits. That’s the definition of 1-1. That sequential items in both sets map to each other. Everything else is not 1-1.
So if Cantor’s proof shows that N is not 1-1 with N, then I must reject the proof as flawed. I don’t need to use the flipping the bits. That’s just one method of many to show that the diagonal does not reach all rows.
@Jim: I should perhaps clarify a couple items.
1. Cantor uses the identity matrix himself because he too knows that it’s the ONLY thing that allows a 1-1 mapping between the rows and digits. Said another way, Cantor uses the identity matrix to select what bits to flip.
2. Cantor uses the flipping of the bits so that the order of the rows no longer matters.
About #1, many people forget that the diagonal (aka. the identity matrix) is what Cantor uses to verify the 1-1 mapping. The identity matrix is the only enumeration that is 1-1 and is why Cantor uses it. Yet, when I mention this fact, I find it funny that people are ok with Cantor using for showing that 1-1 mapping doesn’t exist, but when I point out that it’s the ONLY situation where a 1-1 mapping is possible, people balk. This is why I still hate the fact that mathematicians will use certain things for one goal, but won’t allow it if it doesn’t suit their own predefined notions.
About #2, this implies (ie. is equivalent) that there should be an alternate enumeration of the same set where the length (position of last non-zero digit) is one more than the last row. And once you have this, you no longer need to flip bits to complete the “proof”. It is an irrelevant step. Said another way, Cantor’s diagonal will find a missing number if your list contains two (or more) rows of the same length. But every mathematician on the planet missed this including Cantor himself. Why?
MrX,
Not sure if this is useful.
Another way to think about the identity matrix is to assign a “1” if the row number = the column number and a “0” if it doesn’t to each string.
You have an orderly, predictable way of generating an infinite number of strings with one “1” and a infinite number of zeroes. Obviously, the infinite list does not include all strings.
As far as I can tell, Cantor’s diagonal argument simply points out the same is true for lists of strings with random sequences of zeroes and ones. An infinite list of random strings does not include all strings.
All is bigger than infinity?
@Jim: What infinite list is does not include all strings? The identity matrix? Of course it doesn’t. It’s a proper subset of N if you match by digit. But outside the grid, if you don’t match by digits, you can remap the rows of the identity matrix to N.
So when Cantor produces his diagonal, he can only ever “reach” a number of rows equivalent to a proper subset of N. That’s where Cantor’s result stems from. It does not mean that |R| > |N|. It means that the diagonal is a restricted enumeration.
MrX,
I am requesting clarification on two points:
1. Outside the grid means what?
2. Digits are either “1” or “0”?
Thinking like the Red Queen, there probably is a way to lists all the strings using a 3D cube. Three raised to N is bigger than 2 raised to N.
Correct me if I am wrong, but I think Cantor argued the rational numbers were countable. He listed them in some order and claimed there was a 1 to 1 correspondence with N..
You can think of a rational number as a two dimensional object (a,b) where “a” is the numerator and “b” is the denominator.
Is it worth thinking about listing all strings in some order in a 3D form?
Big picture question: Do we want to count everything?
@Jim:
1. Outside the grid just means don’t use the grid. People are claiming it’s not a mapping, so I’ve been saying “outside the grid” to mean to not use the grid. This also means you don’t map by digits. You only map one row or one list to one row of another list. The internal representation cannot be used in this alternate mapping.
2. Not sure what you’re asking on this one. A string of digits will have 0’s and 1’s for binary or restricted forms.
I don’t really see a way where going 3D would help. I understand the zigzag pattern for mapping Q to N in 2D. Haven’t really thought about going an extra dimension for R since irrationals by definition aren’t ratios of multiple numbers.
MrX,
I am easily confused. I was not sure if your digits were the same as bits.
I became confused about Cantor’s argument when I read a text book that said infinite sets are different from finite ones because the cardinality of a proper subset can be equal to the cardinality of the set. Somehow it seems to contradict the notion of cardinality.
If you are trying to count the irrationals, what happens if you write them backwards. For example, pi backwards equals ……6141.3. Pi has a rational twin since all the digits to the right of 3 are zeroes.
In binary, yeah, digits are the same as bits. In base 10, each digit can have one of 10 values. So in 4567, there are 4 digits. I’ve seen some people use different meaning for those terms. Some say there are 4 symbols and each symbol can be one of 10 digits. But using those terms in that way isn’t really consistent. It’s certainly not used in Computer Science. Most people use the word “digit” to mean a specific position in a number. So I would say the third digit in the above number is 6 for example. Or there are 4 digits.
Cardinality of infinite sets is defined by 1-1 mappings. While the even numbers are a proper subset, you can remap them 1-1 to N. So the cardinalities must be the same.
As for irrationals, writing them backwards doesn’t change anything. There is no “first” digit in such a case. You still have infinite digits and this makes it irrational unless you can find a repeating pattern or prove that the number equals the ratio of two whole numbers.
MrX,
You got the point I was trying to make. If you read right to left from the decimal point, there is no first digit for an infinitely large integer.
You might want to rethink your ratio argument. Since there are an infinite number of primes, there are rational numbers that cannot be reduced to a ratio.
If the last digit of an extremely large and growing integer is odd, about the only thing you know is the denominator of all possible ratios is not two.
Correct me if I am wrong: You are an “uncount” who agrees with Cantor’s bottom line, but not with his proof.
“there are rational numbers that cannot be reduced to a ratio.” Sorry, but that’s the definition of rational. If it doesn’t have a ratio, then it’s not rational. The first digit argument holds no water. Neither does the infinite prime argument. Not even sure what you’re getting at there. Flipping the direction is still the exact same set as before, just using a different representation, but the enumeration is identical. IOW, it’s the exact same set so it will have the same properties as the set that’s written the other way.
There is no such a thing as a growing integer. Do you mean sequence of integers? And what’s this about denominators with whole integers? The denominator is always 1 in that case.
I’m an uncount through and through. I do not agree with the bottom line nor the proof. At one point in the past, I used to entertain the notion that perhaps Cantor’s conclusion was correct (and the proof was wrong). But I now know with 100% certainty that both the proof and the conclusion are wrong.
MrX,
You are quite correct. A bad choice of words not to mention mixing up the rationales with naturals. I sincerely apologize for the confusion.
Why would it not be possible to create an indefinitely large integer or natural number by adding digits to the left of a decimal point?
To Jim:
Natural numbers are all finite, by definition. So for any natural number N, the string of digits representing N (in base 10, or base 2, or whatever base) will always have a leftmost nonzero digit.
Since we don’t bother with showing all the zeroes to the left, of that leftmost nonzero digit, we can always represent a natural number with a FINITE string of digits. Most real numbers require an infinite string of digits to represent them, and that’s why there are more of them. There are more ways to make an infinite string of digits, than there are to make a finite string of digits.
As a thought experiment, suppose we did allow those “infinite natural” numbers. Okay then, let N = …9999999 (i.e., N in base 10 is all 9’s, infinitely far leftward). Now calculate N + 1.
Although trivial, I thought I’d take the opportunity to say I agree with George. 🙂
However, as trivial as these concepts are, I’ve actually heard mathematicians say they disagree that infinitely many naturals require infinitely many digits. The very thought of someone disagreeing with that is hilarious because Cantor uses the identity matrix for that very property in order to select digits along the diagonal exactly because the rows map 1-1 to the digits.
Thanks, MrX…
…for taking the opportunity, to agree on a trivial point.
Please clarify, wether your agreement include the following sentence from my post:
“There are more ways to make an infinite string of digits, than there are ways to make a finite string of digits.”
@George: No, that’s just silly. Both sets have infinite digits. That’s what the last part of my comment was about.
George,
Thanks for trying to be helpful.
You lost me with: “Natural numbers are all finite, by definition.”
Is that a set theoretical definition of the natural numbers or a pre-Cantor definition? Is that the trivial point, you and MrX agree upon?
Like Preemption and a lot of amateurs, I thought positive integers were natural numbers and you could have indefinitely large integers by some simple process. You could string digits together randomly or add 1 forever to the previous integer in a non random process.
As for the indefinitely large sequence of nines, somewhere I read you could put a decimal point in front of it and claim it is the closest you can get to claiming something is probably true without claiming it is true.
On the other hand if you view the sequence of nines as being to the left of the decimal point and want to add one, I guess you would have to carry the one forever to the left. The distinction between “indefinite” and “infinite” gets a bit murky at times.
A natural number has finite digits. That’s the definition. It has always been the definition of a natural number. So yes, this is the trivial point we agree upon.
The rest of what you’re talking about is that you implicitly know there is no limit to the number of digits used. This is what I was talking about when I say that infinitely many naturals require infinitely many digits. But George has a problem with this even though Cantor himself requires this property when forming the diagonal.
So you can’t do what you’re trying to do with a SINGLE natural and add infinitely many digits. Instead, create a new natural for every new digit you add and put that in its own set. That set will then have infinitely many digits. You may then continue your argument that way.
All the “proofs” thus far don’t look at if 1-1 mappings are possible or not. They use the fact that naturals have finite digits. But if infinitely many naturals have infinitely many digits (and they do), you can get around that limitation. All counts refuse to acknowledge this.
Oh, I should add that counts refuse to even look at any flaw in Cantor’s argument even if you were to point it out. They will always try to convince uncounts that they are wrong no matter what. It stops the discussion right there and leads to back and forths that are not very useful. The number of comments in this blog entry shows that. And you can see this with George. I’ve shown him the flaw several times and he glazes over it and changes the topic. The author of this blog is even worse. He once wanted to humiliate me by publishing something about an uncount’s psychological “abnormalities” that would cause someone to believe in something that has been accepted for a very long time.
I write this to warn you in case you find yourself having an argument against Cantor’s “proof”. You won’t get anywhere here or anywhere else. Counts will ALWAYS try to show you how you’re wrong. They will never look at the flaw you’re bringing forward.
Sigh. There’s no edit. Swap count for uncount in my last comment. I’m sure uncounts will get a kick of that.
To Jim:
You need to distinguish between ONE INDIVIDUAL natural number (singular), and a SET OF natural numberS (plural).
If N is one individual natural number, then it’s finite and represented by a finite length digit string.
If S is an INFINITE SET of natural numbers, then no finite digit-string-length will suffice to represent ALL members of S. Strings of length L can only represent numbers below 10^L (in base 10).
George,
I wish it were that simple.
I have no problem with viewing the number line as a ruler with an infinite set of equally spaced markings labeled using the positive integers.
The problem becomes a bit strange when you have two rulers. One ruler can be divided using the diameter of the circle to create the equally spaced marks. The other ruler can be divided using the circumference of the same circle.
Viewed individually each ruler appears to represent a rational set of points. Put them together side by side, each ruler makes the other ruler look like an irrational set of points.
Did Cantor figure out what happens when both rulers coexist on the same number line?
George,
You responded to a post by “Preemption” dated July 5 and MrX commented on your response.
I just now realized Preemption posted two other longish comments on the same day.
Not sure if you noticed.
As a related thought, perhaps any result of “there is no solution” simply rattles people in a primal way… as modern people (and perhaps Americans especially), many of us are indoctrinated to read “no solution” as “waiting for a solution by someone in the future”.
I know that one of the hardest things for my remedial algebra students is to believe or recall that division by zero is undefined in real numbers.
In retrospect it’s funny I said that, because at least one notable Count (John Gabriel, seen on Good Math Bad Math: http://scienceblogs.com/goodmath/2010/02/_so_remember_back_in.php, with arguments similar to some here) also indeed disputes the undefined-status of division by zero (“the universally misunderstood quotient 0:0 (zero divided by zero) and how it is indeed very well defined… If my book called What you had to know but your educators could not tell you is ever published, this knowledge will be revealed.”; http://thenewcalculus.weebly.com/).
To start with, I request all legends to forgive whatever foolishness I write. The correctness of a proof technique basically independent of what being proved. Sometimes what being proved, may be right. But, the method of proof may be wrong (something like a double negation has no effect on a logical statement). If the technique is deceptive, or if the argument is too strong that it is too difficult to counter argue it, we are forced to accept it. The only method to invalidate the proof technique is to disprove something that the technique claims to be correct. It may happen that 99% of the concepts proved by the technique may be correct. And the 1% remained hidden from being revealed. I strongly believe that is what happened in the case of Diagonalization. I won’t say the method of proof is wrong, but I will say I am not convinced that we can put 100% faith in this technique. So unless something have a genuine supporting proof, I think better we don’t build too much on top of it, and we should always be ready to accept a break down, no matter where it comes from(may be from a legend or a novice). Also if something is very critical, we should insist on the need for two to three different methods of proofs, before standardizing the concept. Or the unique proof technique should be built on top of a strong set of axioms(doesn’t matter how complex it is).
Every logical system has a set of rules, deduction methods. The proof thing is pretty formalized.
Dear MrX or anyone who believes that Cantor’s Theorem is wrong,
I would like for you to be correct, but I cannot seem to get past the following proof that says nothing about infinity, so none of the arguments above seem to apply:
Suppose there is an onto function f: A -> 2^A. Let B={y in A: y is not in f(y)}. Since f is onto, there exists an x such that f(x)=B. Then if x is in B, then x is not in f(x)=B. Contradiction. And if x is not in B, then x is in f(x)=B. Contradiction. Therefore, f cannot be onto, so A<2^A. QED
Corollary: Let A=Aleph_0. Then Cantor's Theorem is true.
How can this proof be wrong? Personally, I believe infinity doesn't exist, but I still cannot refute the above logic.
Craig,
You “can’t refute the above logic”, but nevertheless you don’t “believe” in infinity. So I’d like to understand better what it means for you to “believe” in a mathematical theory. I don’t think it makes any sense to believe or disbelieve an axiom such as the axiom of infinity. You choose to use it or not, period.
I you were speaking of a physical interpretation of the real world, then OK. You could argue that “the universe is finite”, that “matter is not infinitely dividable” and so on. For a religion, then again I can agree. You can discuss the existence of God ad infinitum if you like, though in this case – just like an axiom – it’s not provable.
But I refuse to treat mathematics like a religion. Granted they’re not contradictory, the logic and the axioms you choose to use are just a matter of taste and of usefulness.
In my whole life, I’ve never seen, heard, or touched anything that is infinite. And no one has ever proven that anything infinite exists. Therefore, I don’t believe in the existence of infinity.
But if there was a such thing as infinity, then Cantor’s Theorem would be valid.
> In my whole life, I’ve never seen, heard, or touched anything that is infinite.
Neither have I, but this isn’t the point. As I’ve said in my previous comment, you shouldn’t mistake mathematics for physics.
> And no one has ever proven that anything infinite exists.
Mathematical existence means nothing but absence of contradiction. Therefore infinity does exist in math.
> I don’t believe in the existence of infinity.
Then again, you’re confusing mathematics with religion.
For someone born in, say, 80`s everything in foundations of mathematics is given FOL, ZFC etc. It`s really hard or impossible to figure out why foundations mathematics is like that if you don`t look at the original sources. For example Cantor`s philosophy of math is far more subtle than most people understand. I am not claiming that I have read enough about that.
His views seem kind of like Kantian. First there is a for mathematical theory “root” in experience or in physical world let`s say the set consept. Then something like pure reason starts to work on those consepts and they grow away from the physical world or experience. I have an impression that Hardy`s platonism was that the mathematician directly sees the Platonic math world. I don`t see any workings of pure reason there. But that is very different than Cantor`s view, who invented this whole set theory. IMO you can see different though traditions, German and Anglo.
Serge,
There are evolutionary biologists who are creationists/intelligent design theorists, but can still practice their profession. Similarly, you can have a mathematician who doesn’t doesn’t believe in infinity.
Heck, I don’t even believe in the existence of numbers like 2^{2^1000}. Nobody has ever proven to me that such big numbers can exist, so why should I believe it?
What else can I say, apart from repeating that the word “believe” has absolutely no meaning in *mathematics*? I do agree that probably, this number has no existence in *reality* but whenever I write this word, I’m not doing mathematics anymore. Unlike you, many people love mathematics precisely because it’s the only place where infinity has a positive meaning.
Go see my reply to George Kangas. The problem with the proof is that f(x) uses a generator that forces the “for all x in X” generator to actually be “for all x in proper subset of X”.
MrX,
I looked at your reply to George Kangas. I still don’t get your objection to my proof above (which I think was made by Cantor). And I’m not talking about generators in my proof.
Are you saying my proof is wrong because it treats infinite sets like finite sets and different rules apply to infinite sets? Where in my proof is the logic wrong?
Craig: “Are you saying my proof is wrong because it treats infinite sets like finite sets and different rules apply to infinite sets?”
Not exactly. It’s that the subsets of 2^A cannot be listed the same way as A. A has all its elements, but its subsets do not. So how do you check if an element is in the set or not? Do you enumerate them until you see it’s missing or it’s a match? Do you have a list of binary values which would represent the property of being IN or OUT? Either way, the situation is equivalent. What’s important to realize is that each element has turned into a boolean instead of just being an element that is certain to exist. So traversal cannot be done the same way. If you try to do so, you’ll only get a subset of N. So you provide a contradiction only on a subset of all subsets of 2^A which is no contradiction at all.
Here’s a visual. Suppose I label each subset with a natural number in binary. But I also make certain that each label has at least as many digits as the element you’re checking in the subset. For the first subset, I have 1 in binary. For the second subset, I have 10 in binary. So far so good. For the third subset, I have 11 in binary. That’s no good. You’re checking the third element, but my number only has 2 digits. My mapping is flawed. I must fix it to be one to one (element count vs digit count). So I swap this label with 100 in binary. I do this for each subset. And you’ll note that I mapped a subset of N one to one with the elements you are selecting. It’s not just mapped one to one. It is one and the same set. Yes, you go through infinitely many f(x), but not all of them. The way you are traversing them does not allow you to do so. Note that these labels do not modify in any way your “proof” and never alter the order of the elements in any subset. They change nothing about the setup. They are a visual cue to see the proper subset that is traversed. Also, I could swap back all the labels so that they were in their original order and this would not change the fact that you can only list a subset of N in your traversal. Forget |2^A|, you can’t even get through |A| subsets.
So B, when listed as a sequence of boolean values cannot even map to N, only a proper subset of N. This is true regardless of the way you store your subsets.
MrX,
I’ve got to confess, I cannot figure out what your point is. Do you have something you have written up formally that you can link to that may help me?
Let’s start with your conclusion, “So B, when listed as a sequence of boolean values cannot even map to N, only a proper subset of N. This is true regardless of the way you store your subsets.”
B={y in A: y is not in f(y)}, where f is an onto function. I assume you mean list it as a sequence of boolean values (b1,b2,….), where bi=1 if bi is in B and bi=0 if bi is not in B. You are saying that you cannot map B to N, only a proper subset of N. Why not? Let g:B -> N, where g(bi)=j, if i is the jth number such that bi=1? If B is infinite, then we have a mapping from B to N, contradicting your conclusion.
Furthermore, who cares if it cannot map to N? I just don’t see your point. Where in the proof that I gave is the point where the logic fails?
No, you’re using a specific mapping that contradicts the mapping that you state you’re using. Your statements are saying I’m going to traverse a subset of N, but look, I’m declaring that since it’s an infinite list and can map to N OUTSIDE of this setup, then there is a bijection. No, sorry. Doesn’t work that way.
IOW, you’re trying to use two incompatible mappings at once. That’s the source of your conttradiction.
I was trying to figure out a way to destroy the proof I gave and came up with the following idea:
In the proof, I said “Let B={y in A: y is not in f(y)}.” This assumes that B is well defined. If so, the fact that we found a contradiction afterwards implies that f cannot be onto, so A<2^A, as the proof claims. When A is finite, it is clear that B is well-defined. However, when A is infinite, is B well-defined? Modern conventional wisdom says yes. Are you saying no?
If you could prove that B is not well defined, then the proof I gave would be invalid, since anything follows from a statement that doesn't make sense.
Craig: Umm… well, f(y) changes meaning during your proof when you try to see if “y is not in f(y)”. So in that respect, your contradiction is on g(y) and not f(y) as you wanted it to be.
Craig: Wanted to add that your definition of f(y) is somewhat like the proverbial Oracle in the Halting Problem. Not many people have taken time to look into what the Halting Problem Proof means, but it’s about definitions. It doesn’t mean that the halting states don’t exist (all programs either halt or don’t), but that defining the Oracle to use said halting status list is self-contradictory. Your f(y) is like the Oracle. Once you use it the way you do, you contradict its definition. The difference is that this applies only to the way you use f(y), not on f(y) in general.
Hope that makes some sense. Not claiming that it does. It’s what came to mind just now and though it would provide a good analogy. And yes, the irony is not lost on me.
MrX,
You said, “Craig: Umm… well, f(y) changes meaning during your proof when you try to see if “y is not in f(y)”.”
How does f(y) change meaning when I define B={y in A: y is not in f(y)}?
f(y) is a sequential mapping between y and P(A). When you ask if y is in f(y), you create a function that gives true or false, so you change the original mapping into a base 2 representation of f(x). When you ask for the third element of f(y), you are actually at f(8), not f(3). Even if you force the issue and say you are at f(3), then all you’re doing is saying that you only look at 3 elements out of 8. 4 elements out of 16, etc. aka. a proper subset.
For example, take two lists of N, call them A and B. A is the infinite identity matrix with only 1’s on the diagonal and B is the binary representation of all N. If I match elements of A with elements of B via digits, there will be elements in B that are unmatched. Does this mean that |B|>|A|? No. Because A is a restricted representation. Your setup is equivalent to this. You may say that you are matching first with first in each set. No. Sorry. I can re-order B so that all representations that have a single 1 come first in the list by using simple swapping. I removed no element. So all are unique. But now you can’t match any elements that have more than one 1 in it. Note that the swapping is not needed. It’s only a visual tool to help you see what proper subset you are using.
For what it’s worth I’ve had this discussion exactly a year ago today with Terence Tao on his blog (“The “no self-defeating object” argument, revisited”).
I have no problems with Cantor’s proof except that it doesn’t prove what people think it does. In my view it only proves that “…the set of computable reals is not recursively enumerable. (i.e. there’s no computable function whose image is the set of computable reals since there’s another computable function whose image includes one more.)”
It doesn’t prove anything about the set of all (computable AND uncomputable) reals. This may indeed have been caused by Skolem’s paradox because the proof is technically unable to provide any uncomputable reals as witnesses.
Hi Koray, question: Which parts of the proof would you say require that the reals be computable, and require that the list be recursively enumerable?
Referring to WILFRID HODGES paper at point (7) in the proof. It is not clear how first sentence implies the second one. In particular what kind of computation lead from the first sentence to the second one? Any mechanistic way of computing it is requires either infinite time, i.e. not computable, or infinite number of processes. For any finite process it is only possible to test a proper subset of real numbers.
> (7) If n is any positive integer, then bn != ann, and so b != f(n). Thus b is not in the image of f.
All of these values seem to me to be well-defined. No computation is required; we are just following the definitions. If you’re arguing against Cantor’s proof, are you really just arguing that mathematics should only deal with real/computable numbers?
Then what is wrong with uncomputable index
for real 
?
Hi bowaggoner,
The proof proposes a method that can construct a new real from a set of reals by inspecting each real in the set. That definitely works with a set of computable reals.
Why some people assert that it works perfectly well with uncomputable reals is not at all clear to me. How are you supposed to accept the viability of inspecting and modifying a number that you can’t compute?
Moreover, our formal proof systems support only finite formulas and deductions that terminate. We “imagine” to shove in foreign objects labeled with “dot dot dot”s, wave our hands and it somehow works.
Interesting, thanks!
MrY:
> Then what is wrong with uncomputable index $latex[…b_2b_1] for real $.b_1b_2…?
An uncomputable natural number is still a natural number; i.e., it must have finitely many digits.
Koray:
> How are you supposed to accept the viability of inspecting and modifying a number that you can’t compute?
Hmm. I’m not sure (I’m just a devil’s advocate here), but it could perhaps be argued in the following way.
Cantor: Give me a list of real numbers, any list, and I’ll show you how to find a number not on the list.
Adversary: Well, here’s a really tricky list full of uncomputable real numbers that you never could have calculated yourself.
Cantor: That’s true, but now that you’ve given me the list of numbers, I don’t need to compute anything, I just look through the list and construct the counterexample myself.
I hope this gives the intuition I was going for….
Adversary: But look I can take you counterexample, and show that rearranging the list I can put your counterexample in the beginning of the list. Why did you stop here. It will show inconsistency of your logic.
Cantor’s Diagonal Proof uses the notion of infinity to construct an apparent “square” grid of strings: an infinite number of infinitely long strings that generate a diagonal of discrete 0’s and 1’s.
If we can use the exponent 2 with infinity to square it, why not use infinity as an exponent?
If S is the set of all infinite sequences of 0’s and 1’s, then it seems reasonable to think it includes all the possible permutations where 2 is raised to the power of infinity and no sequence is excluded because all possible strings are included.
The length of the rows goes to infinity linearly as the number of rows goes to infinity exponentially, generating a very long, thin “rectangle”. There is no diagonal of discrete 0’s and 1’s; and no need for a diagonal argument.
Does one need countable choice for the diagonal proof? Even if we suppose that that the reals are countable, why we know that they also can be listed?
Ah, my mind is so slow. If r is the bijection (just like in the the post) the list goes r(0),r(1)….
By any chance, are we close to finding an instance of an object in “Godel’s Incompleteness Theorem”?
MrX:
I’m trying to understand your reasoning better. Can you please clarify what is your main claim here:
A: There must exist at least one 1-1 correspondence between the elements of N and R, and moreover you have a proof for that
B: Neither A nor not(A) (what Cantor claimed to have proved) is true in the theory (set of axioms) used by Cantor in the sense that any proof of not(A) can be used to prove A, making the theory inconsistent. Hence Cantor’s proof is no proof at all. Moreover, you have a proof for that.
C: That you have a proof for A, that is not known to be true, but no-one has managed to refute it yet (since any argument they have used so far can be used to refute not(A) as well). Note that C might still mean B is true (i.e. you can’t prove neither A nor not(A) ) but in your opinion no-one has REFUTED your purported proof of A yet.
Based on all I read you must claim either A or B or C. Am I correct, and which one is it?
Milan: Concerning A, I have a proof that doesn’t involve a bijection, but rather the principle that if |A|>|B| and |B|>|A|, then |A| = |B|. So you show a surjective function from R to N (already accepted by everyone). Then I show a surjective function from N to R. QED.
I have a proof with 5 trivial theorems (well, theorem 2 has a limit function to show that the union of all digits of all naturals are countable). I’m in the process of redoing theorem 4 based on one or two comments here that they just didn’t accept it and am writing down what they wanted to see.
About B, it’s not like that. Take set A and B. A will contain naturals numbers listed in base 2 and B will be in base 3. Since I can find representations in B that are not in A, but that all representations of A are in B, then this means that |B|>|A|. Is that true? Of course not. Why not? Because set A is in using a restricted representation compared to B. Well, look at what Cantor uses. His diagonal is a list of numbers that are NOT base 2. They are a restricted form that can be used to list N. We’ll call Cantor’s diagonal set C (where each number can only have one 1 digit and everything else is a zero). Since all representations of C can be found in A (if you match lsb to msb and vice versa) and that there are representations in A that are not in C, does this mean that |A|>|C|? No. C is a restricted set. They both have the same cardinality.
BUT THE GIVEN LIST OF REALS IS IN BASE 2!!! So Cantor will always find a new number because the set in the restricted representation can never match all representations in the set that is less restricted. So you can only match a subset. And you will always find a new number. THIS IS EXPECTED! If you didn’t, you wouldn’t be able to use different bases. The whole point of bases is to permit more different amount of representations per digit. It does not mean that |R|>|N| any more than |N|>|E| (where E is the set of even naturals).
IOW, Cantor’s proof is only valid if you can prove that |N|>|E|. That’s what Cantor’s proof comes down to.
About C: So far, 99.9% of arguments can also be used against Cantor’s diagonal.
I’m not sure I understood what each of the three choices entailed exactly, but my first two paragraphs explain what I have. It’s showing that if there is a surjection in both direction, then |N| = |R|. There is no mapping in that proof. As to the one to one mapping, that’s a different story all together and cannot work in one step. You need at least one more mapping. I haven’t fully worked out the details, but it involves mapping N to representations that are not valid in N, perhaps infinitely recursively (mapping N to Q, then taking that and again remapping to Q, etc. where you keep the right hand side codomain of the mapping). Then you take that codomain and map it to R. So you don’t provide ONE mapping, but infinitely many that covers all possibilities. This allows N to use dedekind cuts by jumping codomains. This is just an ideas and I don’t have a lot of time to work on this. And I find it rather boring.
Does that clear things up?
Sorry for some of the garbled sentences. I rewrote some of them without erasing everything I wanted to rewrite. And there’s no edit function. Also, I said my proof has no mappings. It does, but not a bijection.
Hi again, MrX!
In an earlier (Oct. 24) post, you said:
“Finite naturals use finite digits, but infinite naturals use infinitely many digits.”
I think this sentence may indicate the crux of your disagreement with conventional mathematics. In conventional mathematics, “the natural numbers” means ONLY the finite natural numbers. The phrase “infinite natural number” is just nonsense, to a conventional mathematician.
Let’s call the set of FINITE natural numbers F. What Cantor proved is that F cannot be put in 1-1 correspondence with the reals. Perhaps you should reexamine the proof with this in mind.
That was an unfortunate phrasing on my part. I meant the following:
“Finite naturals use finite digits, but infinitely many naturals use infinitely many digits.”
Do you still have the same objection?
George Kangas: Thought I may as well prove my assertion that infinitely many naturals use infinitely many digits. Suppose I have set A that is represented by only having one 1 digit. It will look like an infinite identity matrix with 1’s on the diagonal and 0’s everywhere else. This clearly maps to N since Cantor himself uses said diagonal. We know by definition that there are |N| rows. Now transpose this matrix along the diagonal and you get the exact same matrix. So the digits have become the rows. Since we know the rows are infinite and the rows ARE the digits, then the digits are infinite as well. QED.
This is the only representation where the mapping is one to one BTW. If the elements were represented in base 2, it would no longer be one to one (this is Cantor’s mistake), but the digits would still be infinite (aka, a proper subset of N).
“your disagreement with conventional mathematics” is a delightful phrase that i shall likely be re-using. Thank you.
> Finite naturals use finite digits, but infinitely many naturals use infinitely many digits.
> … Since we know the rows are infinite and the rows ARE the digits, then the digits are infinite as well.
Okay I’m just student with a passing interest in these topics, but the above assertions are false and anyways the provided proof is incorrect. MrX’s original argument with the decision tree is also dead wrong. For anyone who halfway paid attention in class and worked through a text such as (http://www-math.mit.edu/~sipser/book.html) sees it for the naive and faulty reasoning that it is.
I enjoy lurking on mathematics blogs, but the kind of derailing, threadsitting—basically, asking others to think for them—is distracting. In this particular post, the cognitive overhead of having to skim, was extremely high. You know what I’m talking about if you also had to press Page Down literally one hundred times. It feels unfair.
But of course, life is unfair. I’m emphatically not one of those relatively privileged “Are you kidding?” callers in class, but I suppose that one point of this exercise was to show that everyone eventually discovers their own limits of patience.
Anonymous: “Okay I’m just student with a passing interest in these topics, but the above assertions are false and anyways the provided proof is incorrect.”
You haven’t shown where I’m incorrect. Plus, I’ve shown that both axis are identical. Therefore, the must be infinite digits in N. It’s trivial. I don’t understand why anyone would object to this.
Hi, MrX,
I’m happy to see, that you do know that each natural number is finite. Limited reply depth of this blog prevents me from attaching this reply to the proper post.
Allow me to attempt once again, to reveal the unassailable simplicity of Cantor’s proof. This will be the last time, until the next time.
To sidestep the issue of different decimal expansions representing the same number (e.g., 0.1999999… = 0.2000000… = 1/5), let’s use just this subset D of the real numbers:
D = {.(d1)(d2)…(base 10), such that for each i, (di) = 2 or (di) = 7}.
In other words, all the reals between 0 an 1, whose decimal expansion is an infinite list of only 2’s and 7’s (in particular, with no 0’s). Like .272722277277277277272777722…., for example. No two of these decimal expansions represent the same number.
I will prove that D is uncountable. Then R, being a superset of D, must also be uncountable.
At no point will this proof depend on generators, or traversal algorithms, or any other process taking place over time. ZF set theory posits a timeless, never changing universe of sets.
In many cases, a set may be defined in a style that looks procedural. But the resulting set will be identified only by what elements it ends up having, not by the procedure that generated them or in what order. In other words, for any two sets A and B: A (not =) B if and ONLY IF there exists some element x which is a member of one of them, but not of the other. If there’s NO such x, then A = B (different definitions of A and B, and different orders in which they generated their elements, notwithstanding). This is called “The Axiom of Extensionality”.
One of the unchanging things in this unchanging ZF universe is a set I’ll call M. M = {set of all m, such that m: N -> D}. To banish the error of procedural thinking, I’ll describe M as a book. For each m: N -> D, there is one page of the book on which is printed an array (infinity by infinity) of 2’s and 7’s: the nth row of the array is the decimal form of m(n). This entire infinite book, and every infinite page in it, has been in its final form since the beginning of time.
For each page in that book, there’s real number in D whose decimal form does not appear as any of the rows printed on that page. MrX knows already what that number is; for the benefit of other readers, I’ll spell it out: its nth decimal digit is 9 – d, where d is the 2 or the 7 that appears in row n, column n of the page (note that 9 – 2 = 7, and 9 – 7 = 2). Since this is a number in D, yet is not equal (in decimal form) to any row on the page: the mapping m: N -> D represented on that page is not onto D.
Since no mapping m: N -> D is onto D, D is uncountable.
“At no point will this proof depend on generators, or traversal algorithms, or any other process taking place over time.”
This is like getting into a car and saying that at no point will this involve a steering wheel, gas, tires, a motor or anything of the like. Your comment is pure nonsense.
When you select a digit, you can list how many combinations you can make up by using that amount of digits. Your list is actually longer than the number you are selecting. So what you’re saying is that selecting a digit does not imply a maximum number of combinations for that amount of digits. Sorry, but that’s pure bunk and you know it.
At no point during your selection process do you ever select the last item within that subset. IOW, you can NEVER traverse the entire list. Or if you prefer, you can never select from all elements in the list I have given you.
“In many cases, a set may be defined in a style that looks procedural. But the resulting set will be identified only by what elements it ends up having, not by the procedure that generated them or in what order.”
I understand that. But you must understand that infinity is a procedure that never ends. True that you can take it all together, but that does not restrict us from looking at the individual parts that make up said infinity. So I’m allowed to look at how you make your selections because infinity simply means a set of selections that never end. I note that at each individual selection, you are never on the last element of the subset possible with the digit you have selected up to that point. As such, you can NEVER go through all elements because your selection process is NOT a one to one mapping of the list I have given you. This is true even as you go to infinity because infinity is simply the cumulative result of all individual parts. This means that you will have infinitely many elements that you haven’t selected from even when you go to infinity.
The rest of your argument ignores this fact and as such is irrelevant.
I will say it again, I have proven that you cannot select from more than a proper subset of N.
I will make one last attempt. If you select 1 digit, I have two items in my list. If you select the second digit, I have 4 items in my list. If you select the third digit, I have 8 items in my list. Forget the reals for a second. Just use the naturals. At no point during your selection process will you ever be able to select all elements in N.
Now, you may be thoroughly confused at this point. It’s ok. I will explain what is going on. You believe that if |A|=|B|, then it must be so all the time. Not so. If that were so, then the notion of proper subsets would not be possible. It is possible to have mappings that are NOT one to one. This is what I’m telling you. Your selection process is not one to one with the list I give you. It IS one to one with a restricted enumeration of N though. This is the list where you can only have a single 1 per row and everything else is a zero. I will call this restricted representation base 1. True base 1 would be to have as many 1’s as the row count. Either way is the same.
If you map by digit base 2 to base 3 or base 2 to base 1, you will never get a one to one mapping. For example, if you map all base 2 representations to base 3, there will be base 3 representations that will never be mapped because they contain the digit 2 which is not possible in base 2. Same thing between base 2 and base 1. Base 2 has representations that have mare than a single 1 in it. It also has representations that have sequences of alternating 0’s and 1’s which is not possible in the alternate base 1 representation (where you have as many 1s as the row count).
Even if you map them sequentially from the first item, then the second, etc., you still won’t have a one to one mapping if you look at digits. With 1 digit, base 1 allows 1 element while base 2 allows 2 elements. With 2 digits, base 1 allows 2 elements while base 2 allows 4 elements. And so on.
Here’s a task for you. Prove to me that there is a one to one mapping between base 2 elements and their digits. I’m not asking you to prove that |N|=|N|. I’m asking you to prove that the digits are NOT a proper subset of N when listed in base 2 (or any other base higher than 2). I can guarantee you that the digits of base 2 do NOT have a one to one mapping with the elements they represent. Can they be remapped? Sure. But I’m asking about the base 2 listing before any remapping is allowed.
If you can prove that it is one to one, you win, I lose. If you can’t, I win, you lose.
Hi, Mr. X,
This is intended to be a reply, to a reply you made on November 6.
There’s a theory, called ZF set theory (or ZFC, if the axiom of choice is included). According to this theory, there’s this unchanging universe of things (called sets), and an unchanging relation (membership, i.e., which sets are elements of which sets) between all those sets.
What can be proved about this universe, is governed by a set of axioms. Please look up those axioms on Wikipedia (or wherever). Read them backwards and forwards, and you’ll still find NO MENTION of generators or traversal algorithms.
The diagonal theorem (“for any set S, |S| < |Powerset(S)|"), is a very elementary consequence of those axioms. It's just too damn simple to be wrong — the proof is too short to hide a mistake for 100 years. If you believe the ZF axioms, then you have to believe the diagonal theorem.
So, since you DON'T believe the diagonal theorem, it must follow that you don't entirely believe the ZF axioms. And that's perfectly fine, MrX. Axioms are just opinions and intuitions made formal, and Cantor and Zermelo and Frankel had different opinions and intuitions about infinite sets than you do.
I suggest you examine the ZF axioms very closely, and decide which axiom(s) that you disagree with. If those axioms really are wrong, and you really know why, then here's how you could prove it: use the axioms themselves, to prove a contradiction. Then you'll be listened to.
warmest regards,
George Kangas
George Kangas: “Read them backwards and forwards, and you’ll still find NO MENTION of generators or traversal algorithms.”
So you’re saying there’s no point in discovering the implications of those axioms? That the axioms are the full extents of the rules of this formal system? Gotcha! That’s sarcasm BTW.
“It’s just too damn simple to be wrong — the proof is too short to hide a mistake for 100 years. If you believe the ZF axioms, then you have to believe the diagonal theorem.”
That is incorrect. The proof was known to be wrong for a very long time. Over time, mathematicians decided to ignore the problem with it. And within the ZFC axioms, Cantor’s diagonal proof is trivially wrong.
“So, since you DON’T believe the diagonal theorem, it must follow that you don’t entirely believe the ZF axioms.”
No. That is incorrect. Also, you need the axiom of choice for Cantor’s diagonal to work.
“I suggest you examine the ZF axioms very closely, and decide which axiom(s) that you disagree with.”
I don’t disagree with any of them. But I do think the axiom of choice would need some clarification within infinite sets because what you’re trying to do with it is self contradictory.
“If those axioms really are wrong, and you really know why, then here’s how you could prove it: use the axioms themselves, to prove a contradiction. Then you’ll be listened to.”
I already showed the flaw many times.
I can prove that the digits of N and N map one to one only when you use a restricted representation where you only have a single 1 per row and everything else is zero. The digits map one to one with the rows. So if there are |N| rows, there are |N| digits. QED. I’ve just proven that there are |N| digits when enumerating N in this way. Not arbitrary, not finite, but infinitely many digits. I still get people who would ask me what finite element (note that they themself call it ONE aka FINITE) has infinitely many digits. I just have to scratch my head. These are the very same people that are trying to say I’m wrong.
For all other bases, you get into problems. There won’t be a one to one mapping between digits and rows because each digit will multiply the number of rows possible by its base. So any time you select a digit, you are in effect saying that the set has at least b^d elements that use d digits or less.
The implication of this is that you are changing the mapping when you select by digit. IOW, you want two different mapping to hold at the same time. This cannot happen unless you use the same mapping (which cantor does not). Either choose the restricted mapping or choose base 2 mapping. Pick ONE. If you pick both, you will get a bogus contradiction.
I will end with the following. If I look at the even elements of N and match to N via base 2 representation, I will note that not all elements of N have been mapped to. Does this imply that |N|>|E| where E is the set of even numbers? Of course not. Cantor has the EXACT same issue. He is using a restricted mapping. And before you say he isn’t, that is not acceptable. You can’t just do something and then say you aren’t. His diagonal selection is very much a mapping. It is the restricted mapping I talked about earlier and can only map to a subset of N in base 2. So no matter the list of reals I give you, you will only ever select from a subset of N.
George,
Nice point. I like this question.
It happens that this month’s Mathematical Intelligencer has an enjoyable retrospective article by Reuben Hersh titled “Paul Cohen and Forcing in 1963”. This article accessibly discusses many of the same subtle topics as this thread’ in particular it describes the necessary-yet-seemingly-paradoxical existence, and the practical proof-theoretic applications, of “Count” models of “Uncount” set theories. Hersh also engagingly describes how he came to write jointly with Cohen their celebrated Scientific American article “Non-Cantorian set theory” (December 1967), which introduced these ideas to a wider audience.
(It’s highly regrettable that both of these articles reside behind paywalls 🙁 )
George Kangas,
“Let’s call the set of FINITE natural numbers F.”
Does this not contradict the very definition of N? Clearly F !=N.
We are talking about 1-1 correspondence beween N and R.
F does equal N; I just used the alternative name F for the benefit of MrX, or whoever else believes that some natural numbers are infinite. The accepted definition of N includes only finite numbers as members of N.
Note that while each member of N is finite, N itself is not finite (because there is no highest natural number).
@Geoge Kangas: I truly admire your patience with Mr. X (also that lovely proof of Cantor’s theorem). I wish I had more professors as patient as you.
Dactyl: I don’t believe that one (aka finite) natural has infinite digits. I’m saddened that anyone would think that.
I still don’t follow–
How can the set N become infinite if each of its members is finite? This itself is a paradox or some problem with some axiom (or the definition of N).
N= {1, 2, 3, … ?}
@ Javaid Aslam:
Okay, let F = {set of finite natural numbers}, and suppose that F is finite.
Since every finite set of natural numbers has a maximum (just list them in order, and choose the last one), let m = maximum(F). Then m is finite (since it’s in F), but m + 1 is infinite (since it’s not in F — it’s greater than F’s maximum).
What is the value of m, the greatest finite number, so that m + 1 will be infinite?
This post left out an important case: Believing/Knowing that reals are uncountable, but still rejecting Cantor’s “proof” of the fact. Assuming countable reals won’t help convincing those people.
I agree that people who can not see why this proof is correct are most likely troubled with understanding “contradiction proofs”. I have heard mathematics students say “Proof by contradiction is not a proof”. We use them all the time in computer science so I don’t understand how you can not get it. Maybe it is because mathematicians (afaik) rarely get a formal introduction to logics?
“We were about halfway through the semester, when a student asked a question that was essentially: what is a Turing Machine?”
Look on the positive side. He didn’t ask: Who invented the Turing Machine?
I’d like to know what people in this thread believe. How many digits does N require to list all elements? IOW, if I listed all of N in a similar fashion that Cantor lists the reals, there would be how many columns for the digits of N? In base 2? And in base 1 (where you can only have one 1 digit and everything else is a zero)?
I proposed the infinite identity matrix in base 1. Since the digit index and the row index are mapped one to one, then if the rows are infinite, so must the digits.
Only if N doesn’t use infinite digits can N and R be of different cardinality. That poses a serious problem for Uncounts.
It doesn’t to me, because I haven’t the faintest idea what “N doesn’t use infinite digits” means.
Dear MrX,
I admire your persistence and passion, but I am not sure I understand your argument.
Are you arguing the Reals and the Naturals are equally countable and/or uncountable?
If so, are you trying to develop a “nominal” diagonal argument to counter those no-count Uncounts?
1 = 1
2 = 11
3 = 111
4 = 1111
5 = 11111
I think they “hear” a lot of counter arguments about counting and infinity:
“See here, here, here, or here for some examples.”
Don’t know if they have heard that one.
It is not an argument. It is a question. I want to know what mathematicians believe. I get different answers depending on if it relates to Cantor or not. So as the author of this blog said, let’s show our hands. What do you believe? Are there |N| columns for the digits of N represented in base 1, base 2, etc?
MrX, your repeated question intrigues me.
The set of all digits of all elements of N is countable, but the set of all digits of all elements of R is not. Note that each element of N has finite digits; whereas each element of R has infinite digits — that is the key difference.
I will show you my hand. Take elements of N to be binary (big-endian, starting with place p=1). Then the string of all digits of all elements of N is: 110111001011101111000… More specifically, for any natural number n, the digit d(n,p) is associated with, and appears at, the index: sum(i=1, n-1)[floor(log(2,i)+1)]+p.
Examples: The first binary digit of n=5 is d(5,1)=”1″ and appears at index = sum(1,4)[floor(log(2,i)+1)]+1 = [1+2+2+3]+1 = 9. The last binary digit of n=8 is d(8,4)=”0″ and appears at index = sum(1,7)[floor(log(2,i)+1)]+4 = [1+2+2+3+3+3+3]+4 = 21.
This mapping satisfies the definition of countability for the set of all binary digits of all elements of N. And it answers your question, “How many digits does N require to list all elements?”, namely: a countable infinity.
Delta: If what you say is true, and I agree 100% with it, then Cantor cannot be right. It is impossible. Your assertion that the aggregate concatenation of all digits of all elements of N in base 2 (or whatever other base) is countable, then this is contradictory to Cantor’s proof.
I can create a different representation of N where the amount of digits doubles for each element of N. This maps one to one with the infinite binary tree. To picture it, each element of N maps to each row of the infinite binary tree. And each digit of each element maps to the nodes on each row in the tree. As such, every node of every infinite path is mapped one to one to a digit of my representation of N.
So whatever you’re using to distinguish between reals cannot be more than what is used to distinguish between naturals.
QED.
Before we leave this delightful Gödel’s Lost Letter post, please let me recommend to Count and Uncount alike a thoughtful essay by Chandler Davis titled The
Role of the Untrue in Mathematics, which concludes:
An essay well-worth reading! 🙂
do counts believe that the power set of natural numbers is countable?
A Salute to the Vets from Here to Eternity:
11/11/11/11/11/1111111111111111111111111…..
It’s not a question of “If Cantor’s proof is wrong”. In fact, Cantor does not have a “proof”. His diagonal argument is completely wrong.
I guess you won’t post this, will you Lipton? Let’s see, because you think I am anti-semitic?
Lipton, you are a pathetic fool! And I just love abusing you and others like you verbally.
One last idea…
This is a bit late, and I don’t want to start off any debates, but perhaps a better tack is not to suppose that the given function is surjective, and then show it misses an element, but to take _any function whatsoever_, and then show it misses an element. This may sidestep claims like ‘you took it to be not surjective to start with, you fool’. Showing every single function N –> 2^N is not surjective feels a lot stronger than using a proof by contradiction, even if it is the same result (at least in classical logic, but let’s not go there). If people want to argue with that, then they are arguing about the definition of a function, rather than the definition of a surjective function between infinite sets.
Hi, David,
Please see my post from Oct. 24. I prove that any f: X -> 2^X is not surjective, without use of “proof by contradiction”.
Of course, MrX was not satisfied.
regards,
George Kangas
Dear George,
In your proof chose mapping that lead to S=empty set, then the number that is not represented is 0, But it does not have to be represented – we are looking for open interval. So the proof shows nothing.
Hi, MrY,
In that proof, numbers (real or natural) are never referred to. What’s proven, is that for ANY set X, and any f: X -> 2^x, that f is not surjective.
But, if X were the natural numbers, and the map f : N -> 2^N were such that S is empty, that would mean (by definition of S): for all n in N, f(n) contains n. Thus no f(n) is empty, so the empty set (which is in 2^N) is not in the image of f. So f is not surjective, so this case presents no difficulty for the proof.
Notice that I still haven’t referred to real numbers. There’s a subset D of real numbers, those which consist of a decimal point followed by an infinite string of just 2’s and 7’s (see my post of Oct. 30), which is in 1-1 correspondence with 2^n (so that D is also uncountable). Then, since this subset of the reals is uncountable, then the entire set must also be.
You mention something about an open interval. My set D isn’t open, nor does it contain any open interval, but that’s not an issue in any way.
regards,
George
George, I have no objection against Power set proof. The mapping from power set to real numbers does not prove anything. The pinned point corresponding to empty set correspond to 0. in Cantor set. but 0 does not have to be represented, since after tangent transformation that goes to infinity. But than you cannot say anything about the rest of the correspondence.
And with this respect I do not understand why given any reasonable complicated mapping I can rearrange rows in a way that all numbers in the diagonal will be 0 in binary representation, that in the Cantor construction we get 0.111.and.so.on.= 1. This is equivalent to pinning an empty set. And again 1 is the value outside of the range of real number needed to be represented. This logic says that Power set is so powerful that it can represent all the real numbers + infinity.
Another thing I do not understand is the following. For random infinite square table with countably many rows filled with 0 and 1 with probability 1/2. For every n and fixed first n-1 bits there are countably infinite rows with n-th bit ‘0’ and countably many rows with n-th bit ‘1’. When one is constructing Cantor number, at what stage (for what n) one of these countably infinite subsets becomes an empty set? I do not see one, help me out, please.
Therefore, it seems that Cantor arguments per se are not sufficient. This is related to our conversation with Gowers. The count vs uncount seem to be different in the order the limit is taken – rows first or columns first, and I think this is what Prof. Lipton means by show your cards.
Minor nitpick: assuming a surjective function exists and then showing that this leads to a contradiction is not “proof by contradiction”. It’s rather a “refutation by contradiction”, a.k.a. “reductio ad absurdum”, and is perfectly constructive.
David Roberts: The problem is that all the proofs I’ve seen so far map to a subset of “any function”. So there’s an element missing, eh? That doesn’t impress me much when you’ve designed it that way.
Prove to me that the list Cantor uses isn’t a subset of what I give him. Or simply prove that the digits of N map one to one with the elements of N when using base 2. IOW, prove that the digits aren’t a proper subset of the rows. No remapping allowed. They must remain within the grid. So forget R for a second. I just want to know if Cantor can even cover N rows when he maps digits to rows. Do this and I’ll believe in Cantor’s diagonal. Don’t, and you have to accept that he can only use a subset of the list I give him.
Dave,
You might want to wander over to GASARCH’s “Computational Complexity” blog and look at the post “What is a Simple Function?” (August 8, 2011)
Like this blog, the question was inspired by a disconnect between what the professor was thinking and what students might think.
At the time, I was thinking of jumping in with my 2 cents worth with the idea that counting is a simple function. Fortunately (in light of this discussion), I got into a metaphysical argument with myself:
1. Isn’t using numbers to label things “somehow” simpler than counting?
2. Does the identity function, f(x)=x, “somehow” capture this simplicity?
Bottom line there, I got to worrying about what are the “simplest functions” and how would you define them?
I no longer take it for granted that “I know what a function is” other than it seems to be a useful Organizing Principle.
Reminds me of the Groucho Marx joke John Sidles told:
“These are my principles. If you don’t like them, I have others.”
Hi all, I’m a count. I think Cantor’s proof does have a flaw and I think a lot of confusion comes from defining existence and construction.
For something to exist, does that mean that it has to be explicitly defined and constructed? Cantor “constructs” a real number out of a mapping that may not be possible to “construct”. It may still “exist” though. I think I understand his approach perfectly well, but we live in a countable world. Every mathematical concept is countable. What need is there to fuss over the uncountability of the real numbers when we will only ever conceptually consider a countable subset? Algebraic numbers, solutions to problems, geometrically significant numbers. All countable. The only thing we can’t do is take a list of every single number and arbitrarily switch the decimal digits around and call that a new number. It isn’t a normal mathematical operation anyway, just a contrivance to prove an abstract idea with no application.
I think it’s easy to forget how big and powerful countable really is and how conceptually vague and extreme uncountable is.
> Cantor “constructs” a real number out of a mapping that may not be possible to “construct”. It may still “exist” though.
Can you elaborate please? What may exist? A number, a mapping?
The existence, btw, is defined in the ZFC axioms, are you saying that Cantor has broken some axioms in his proof?
> but we live in a countable world
First of all, are you claiming that you know for sure that there are countable number of starts in the universe?
Secondly, *it does not matter*, the concept can be useful even if it did not came from the “real world” (again, we might as well just live in a Matrix, it does not matter).
> I think it’s easy to forget how big and powerful countable really is and how conceptually vague and extreme uncountable is.
What exactly is “conceptually vague” is there in the concept of uncountability?
and other set? Can we construct a non-bijective mapping between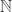 
and other infinite set? Can we show that for some sets it is not possible to construct bijection from them to 
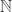? This pretty much sums up the basics of uncountabillity.
Does the set of natural numbers exist? Can we construct a bijection between
oh: “Can you elaborate please? What may exist? A number, a mapping?
The existence, btw, is defined in the ZFC axioms, are you saying that Cantor has broken some axioms in his proof?”
The mapping between base two columns for the digits and the rows is not one to one. So the diagonal can never traverse all rows. In fact, he can’t even get N rows, only a proper subset of it. So the diagonal cannot be constructed as defined.
I’m rather saddened that mathematicians still believe in Cantor’s diagonal. Not ONE person here has had a valid objection to what I’ve proposed. I did get about TWO requests for clarification which were great. When I did so, they never returned. The only objections are things like asking for a digit at an infinite position. Seriously? Or that I wasn’t happy with certain axioms. Or that it’s ok to use the axiom of choice in an infinite set without understanding that this affects the proper subset you are selecting into. The sheer lack of understanding here by both the commenters and the author of this blog are astounding.
The author wanted to know why a lot of people have a problem with Cantor’s diagonal. It’s easy. Cantor uses infinity as if it is complete and finite. It’s an old objection that still stands. Mathematicians of the day would tell him this directly. Today, it seems that it’s a battle between the mathematicians of old and the mathematicians of today. One of you is wrong. One of you is right. Both of you are mathematicians.
Every kid that learns to count know that for any given amount of digits, there are more rows than digits. As such, every elementary child that’s gone to school knows that the mapping between N and its digits is not one to one. Yet no mathematician here is willing to acknowledge this. Cantor can go to infinity, but he will never reach the last row in a list of N reals. Never mind R reals.
You know what I’m normally told at this point? That we already know that a proper subset of N and N map one to one. And there’s no convincing them of the implications of this. It’s like you said there was an ocean between the US and France and they decided to drive to the other side anyhow as if their statement had no consequence to their methods.
I don’t know how many times I have to say it, but one to one mapping are a possibility, not a requirement. If you map digits to rows, and you select as many rows as there are digits, you still have infinitely many rows that you’ve missed because the mapping is not one to one. In fact, I can tell you exactly what the difference is at each digit.
So Cantor can indeed reach all |N| digits, but those are mapped to a subset of N, or rather a subset of the rows. Take the even numbers and map them to the even numbers of N. This is not a one to one mapping. The thing is, some people think that if the evens were at the beginning, then if they continue to infinity, it will magically become a one to one mapping. For example, I’ve said that E is mapped to the even elements of N. In N, if I reach an element that is odd (and isn’t mapped), I swap it with an element further ahead that is. If I can continue doing this infinitely. All the even numbers will be at the front. And yet, I will never cross all elements of N.
Cantor has cleverly devised such a process where all the non-mapped elements are at the end of the infinite list that his diagonal can never reach.
Note that the swapping is NOT necessary. It is a visual thought experiment to show you how it’s possible. Cantor very much restricts any list you give him. He will never use the entire list. If he did, he would break the mapping between digits and rows in base 2. In doing this, he will be using a custom mapping that is contradictory to the non one to one mapping just described.
Like I’ve always said, Cantor’s diagonal argument is self-defeating. If it succeeds, it must fail.
Dear MrX,
On November 8, 2011; I asked for clarification:
“Are you arguing the Reals and the Naturals are equally countable and/or uncountable?”
On November 19, 2011 4:32 pm; you responded:
“It is not an argument. It is a question. I want to know what mathematicians believe.”
Then on November 20, 2011 5:48 pm; you posted:
“I’m rather saddened that mathematicians still believe in Cantor’s diagonal. Not ONE person here has had a valid objection to what I’ve proposed. I did get about TWO requests for clarification which were great. When I did so, they never returned.”
I have returned, but I am a bit confused.
Are you arguing that there is a problem with Cantor’s proof, or are you taking a poll?
I am not sure if you noticed, but the folks who believe Cantor’s proof is correct seem quite happy with their beliefs and they do seem to have the majority of the heavy hitters on their side.
It might be a bit premature to declare victory.
Jim Blair: “Are you arguing that there is a problem with Cantor’s proof, or are you taking a poll?
I am not sure if you noticed, but the folks who believe Cantor’s proof is correct seem quite happy with their beliefs and they do seem to have the majority of the heavy hitters on their side.
It might be a bit premature to declare victory.”
And yet NO ONE has a SINGLE valid objection. Anything that’s come up has already been verified by other mathematicians. Besides, if you look, the only objection is that digits are finite. That can’t be a valid objection by definition.
Also, in earlier comments, I’m stating there is a problem with Cantor’s proof. In another comment, I’m asking what mathematicians believe because they change their tune depending on if the name Cantor is uttered or not. Right there, that’s a red flag. So maybe I can’t declare victory, but the “heavy hitters” are unknowingly waving a white flag.
It would be easy to have George Kangas’s above proof checked by an automated proof assistant. But Mr X would still argue that the assistant is flawed, that the axioms are wrong, that no sensible person can believe them, and so on. This is materialism pushed to its utmost: believing only what you can see with your eyes or what you can touch with you hands. It implies the denial of any theory by refusing to admit the brain as a relevant instrument of observation. In my opinion – besides the unhealthy attitude of equating theory to reality – it runs counter to the very notions of science and even democracy.
Serge: that would prove nothing — everyone knows computers have been brainwashed to believe the Cantorist dogma!
🙂
Dear Serge,
You might want to take a look at “Empirical Humility” posted October 12, 2011.
In Theory the Titanic was unsinkable.
Yes, I remember that post well. In it I expressed the idea of neutrinos being lighter than light. I don’t know if relativity should be compared to the Titanic but I respect this opinion.
Cantor had exceptional mathematical insight and intuition, the diagonal argument is brilliant (and completely correct), and the reals really are uncountable.
Dear MrX and some other Counts: At first I thought you were role playing the devil’s advocate, or perhaps pretending to channel Kronecker!
But if you really are serious: Let me explain why many people will not accept your protestations. It is because you directly question the logic of the diagonal argument. In a nutshell, the diagonal argument tells you that if you generate an infinite LIST of reals, then we can GIVE YOU a real number which will not appear ANYWHERE in this countable list. It is that simple. To be taken seriously, the burden of proof is on you to show how this extremely simple (and beautiful) idea could possibly be wrong.
I also cannot accept somehow to say that for all practical purposes we can get by with countable sets. We can’t, because we do really need uncountability to get positive Lebesgue measure on the real line. And without Lebesgue integration, we would need to give up the mathematical technology of
spaces, Sobolev spaces, etc., which are essential even outside mathematics (e.g., in physics). We would even lose the Cantor set and fractals! It would almost be a return to the 19th century.
Dear Gandhi,
Kronecker may have had some quaint notions about protecting new generations of mathematicians from Cantor’s ideas, but he too was a progressive mathematician:
“The modern definition of a group, using an axiomatic approach, was given in the commutative case in 1870 by Kronecker …..”
Stephen Hawking of black hole fame edited a book he titled “God Created the Integers”. Cantor was one of his 31 mathematicians that changed history, Kronecker wasn’t.
On the other hand, the title of the book comes from a quote attributed to Leopold Kronecker:
“God created the integers. All the rest is the work of Man.”
Big Universe. Lots of room for differing opinions.
Very interesting, thanks.
“In a nutshell, the diagonal argument tells you that if you generate an infinite LIST of reals, then we can GIVE YOU a real number which will not appear ANYWHERE in this countable list.”
so what?
i double my numbers and therefore there is a little bit of space for your allegedly not appeared number
and i can give you a few more integer for every of your numbers,
my daddy is stronger than your daddy.
haha
“It is that simple.”
haha
give me a real , i give you rationals +1, …but wait:
+2, or let´s have look: twice … no:
i give you for EVERY f..ing real countless rational numbers, listen :
for every bloody real, what about THAT? you just cannot deliver right now? oh , what a pity,
haha
WHY NOT?
(maybe because of a little bit of circular reasoning?)
haha
my daddy is stronger than yours, okay?
you comical ali of comical math.
and i am not a “count” or something else comical what so ever…
count…uncount …haha …you all need to have a little bit of fresh air…
> my daddy is stronger than your daddy.
In set theory this can be rephrased as: “uncountable sets have higher cardinality than countable sets”.
But your “beautiful” proof is ugly and wrong. It’s also not simple at all. If you think it’s simple, then there’s no way you’ll ever see the flaw. The flaw is quite clever. It is very difficult to see, but at the same is trivial. The flaw is that the diagonal only samples into a subset of any list that is given to you. Cantor uses this fact to “prove” that the reals are uncountable, but what he has in fact proven is that his proof is bogus in that his diagonal can only work for a subset of N.
As a very first step, would you agree that if Cantor’s diagonal can only work for a subset of N, that his proof is bogus? Ok, good. Now prove that the digits are one to one with the rows.
More than that, if there really is a mapping between R and N, you can’t even use a one to one mapping between the digits and the rows because that would nullify (or contradict) any other mapping that would be one to one with R.
As I’ve said, it’s a very UGLY non-proof. If Cantor’s diagonal proof is self-defeating. In ALL cases, it proves itself bogus.
I will try one more explanation. Does Cantor’s diagonal work with finite (sub)sets of naturals? If there are 8 elements, can you form a diagonal? No, you can only reach 3 elements. If there are 16 elements, can you form a diagonal? No, you can only reach 4 elements. On and on. This will never change. Note that there is NO digit at an infinite location. So this clearly shows that the mapping between digits and elements is NOT one to one.
Now, you may WANT to say that you’re mapping the first digit to the first row, but you can’t do that because the digits indicate how many rows you can represent with said digits. If you are using a diagonal where the digits are important, you cannot discard this mapping. So all you’re doing is confirming that you’re choosing a proper subset of the combinations at any given digit. This will be true for all digits. All infinitely many of them.
Yes, you go to infinity. But all you’ve done is map a proper subset of N to N. IOW, a proper subset of digits (aka the rows) to the digits. So Cantor’s diagonal doesn’t prove anything. And as I said, even if the digits did map one to one with N, then that would contradict a mapping with R. Note that this doesn’t mean that there is no mapping. It simply means you’re using two different mappings at once. Cantor’s diagonal is so trivially bogus, that it’s really cringeworthy to think that anyone would believe in it.
You may disagree with my interpretation, but what I really believe Cantor was doing is using exactly the flaw I’m mentioning on PURPOSE. I left a trap and I thought someone here would bite. No one did. So I can’t tell if mathematicians believe that the digits map one to one with N rows or if they believe otherwise. See, Cantor believed otherwise.
This flaw is what he thought was correct. He’s actually saying that yes, you need a proper subset of N digits to represent N elements and this is exactly what he uses in his proof. So if you use N digits (instead of a proper subset of N), then you’ll have MORE than N elements and he formed a diagonal to prove this fact just as you would with finite sets. Remember that Cantor saw infinity as a complete finite set. It’s a truth that cannot be escaped. What he also didn’t realize was that it’s a bogus interpretation of the results regardless. For ANY given amount of digits that maps either to N or a proper subset of N, the resulting rows can always be remapped to N.
In other words, Cantor’s diagonal attempts to “prove” the following:
1. A proper subset of N digits can produce N elements.
2. Therefore N digits can produce greater than N elements, aka R.
Allow me to show the finite version of this proof. After you’ve understood it (it’s trivial), replace 4 with N… replace 2 with a proper subset of N… and replace 16 with R.
1234 (<-digits)
0000
0001
0010
0011 (with 2 digits, this is the last element in the set.)
0100
0101
0110
0111
…
So if you form a diagonal, you'll never get all reals because Cantor believes that this will only grab a proper subset of them just like what happens with 8 naturals or 16, or 32, etc.
In the above matrix, pretend that 2 digits is actually a proper subset of N digits as mentioned earlier. Just replace it. And that 4 digits is actually N digits. So if you form a diagonal, you will get 4 elements which is now N elements. As we can see, there are MORE elements in the list that cannot be mapped into these N elements. The number 4 and above. These are the numbers formed by the diagonal. Get it? No matter what 4 elements I give you (or rather any N reals I give you), there are always more numbers that can be produced.
That is all that Cantor is showing. And I believe this was his intention all along. That's his proof. This is why I kept asking if people here believe if the catenation of all digits of all elements of N in base 2 is countable. If so, then all sets in #2 above are also countable. End of story. Cantor was wrong.
I can guarantee you this is what Cantor believed. The guy was a complete nutjob. He didn't understand anything about infinity. He went to the insane asylum because he couldn't come to grasp with it. And now, we have mathematicians that should know better following in his footsteps and it's supposed to be the "counts" that are the whackjobs? Yeah, sure. I REALLY dislike being called names. So I don't say that Cantor is wrong because of some irrational (pardon the pun) belief. I SEE IT. It clicks. And no one here or anywhere else even wants to look at the flaw. Any time they come close, they run away intentionally. So I know with 100% certainty that those who believe in Cantor's diagonal proof are biased in a religious fanatic kind of way. There can be no denying it. What I'd like to know is why? You've called it a beautiful proof. How is it beautiful? It's wrong. It's ugly. And it takes something akin to religious fervor to believe in it. And the damndest thing of all is that the above is the ONLY way you can get more numbers than there are in N. By using a proper subset with a SPECIFIC non-"one to one" mapping.
MrX,
Do yourself a favor. Learn some basic set theory. Learn the notation. Then if you still have your misconceptions, come back and phrase your arguments in terms we can all understand. It’s impossible to even disagree with most of what you’re saying, to the extent that it’s utterly incoherent. The only thing I can discern enough to disagree with is that you seem to be afflicted with a belief that proper subsets of the N cannot have the same cardinality as N, which they most certainly can. Take the set of even naturals; they are a proper subset of N yet isomorphic to it. In fact any infinite subset of N is isomorphic to N.
pelotom: “The only thing I can discern enough to disagree with is that you seem to be afflicted with a belief that proper subsets of the N cannot have the same cardinality as N”
Pelotom, I’m sorry to say, but you can’t understand infinity even if your life depended on it. Yes, a proper subset can be REMAPPED to N. That’s the definition. But a proper subset is initially a mapping that is NOT one to one. Understand that? Ok. Good.
Dear MrX,
I agree with pelotom that you should learn/relearn set theory. (I highly recommend a book on real analysis by W. Rudin, I found it excellent. )
To be blunt, you do not sound mathematically literate.
For example, do you understand that a power set has cardinality strictly larger than the original set? If NO, you obviously need to learn set theory. If YES, you must accept, logically, that the reals are uncountable.
It is “Catch-22” situation for you: Either humble yourself and learn mathematics properly, or else concede that the reals are uncountable.
Gandhi Viswanathan: I would say that it is you that need to hit the books. You’re using a circular argument. If we take what you say, then why ask the question at all in the first place? Why ask if there is a one to one mapping?
See, you can’t even understand that there’s a question there. You accept it as gospel truth.
Gandhi Viswanathan: I’ve ordered the book. BTW, you should look into the question of cardinality and powersets. You’re saying it’s a done deal. It isn’t. Also, this is a blog. I find it rather difficult to include mathematical notations.
1. There is an injection f(x) = 2^x (exponentiation) where x is the digit index.
2. Because of the injection and it’s not a bijection, the set of digits D ⊂ N.
I think most mathematicians don’t agree with the above. If they did, Cantor’s diagonal is trivially bogus. First off, we know we can find a bijection between D and N if a remapping is allowed. Cantor disregards that fact.
So what Cantor then proceeds to do is exactly as above, except that instead of a subset of N for the digits, he uses N. |f(x)| is no longer |N|, but |P(N)|. In the above case, if you were to create a diagonal with a DxD matrix, you’d only cross a subset of N because D ⊂ N in this particular setup. If you do a NxN matrix, then the same thing happens, you will cross a subset of R. The problem with the proof is this. If D can be remapped to N, then there is no proof in Cantor’s diagonal that N can’t be remapped to R in the same way. The technique that he’s using is bogus when it comes to D and N. So why should it suddenly become valid with N and R?
Bogus proof.
Sorry, in statements #1 and #2, I’m talking about listing the naturals. And then show how Cantor uses the same technique that doesn’t work in 1 and 2 for reals.
And a correction, since f is an injection, when Cantor tries to apply the same technique with reals, |f(x)| is |N| instead of |D|. So Cantor sets up the contradiction instead of it being a consequence of set theory.
that is my “nichtganzso”-diagonalbeweis:
YOU give me a real, i give you infinitely many rationals:
lets start with pi:
i give you all rationals between 0 and 1
you give me e, i give you all rationals between 1 and 2
you give me sqr 2, i give you all the rationals between 2 and 3 ….and so on
now then, whats your next move? or should we start with another real?
you can give me all reals, i give you infinitely many rationals for every real of you back.
this is pretty fair, isn´t it?
now i have “proved”, that there are infintly more rationals than reals,
!?
all members of IR times infinty and voila, you just have got IQ. or just a small part of it.
that´s the way how cantor came closer to god,
and to the funny farm.
knorke94:
Well done, you’ve shown that if I could give you an enumeration the reals, you could provide an onto function from the rationals to the reals. Unfortunately since the reals are uncountable, I can give you no such enumeration…
i told you so!
you cannot deliver,
but i can:
(of course with your help of the ability for “constructing infinity”)
infinity times for each of your numbers.
that is the problem of hare and hedgehog. here in this game i am the hedgehog and you are the hare. (grimms tales).
in this game YOU have to hold still and i move and i am always there, not like the other game, were you can build new thing and the rationals or integers has to hold still.
i am not interested wether the reals are countable or not, give me just your funny reals, one after another, is that to difficult for you? JUST DO IT!
i know you are so uncountable, you do not have plenty of time for that, the other numbers are stucked in a REAL traffic jam. but why so in a hurry? so uncountable?. anyway, nobody cares . so ,just one after another. it works, believe me
and all your phantoms are gone. who cares about countability when he has got infintly many attempts…that is quite a lot.
you deliver and i deliver. fine. what coulf be a problem. you cannot come to an end. me too.
the whole thing is biting itself. circle definition.
you cannot define one real (f.e. pi “perfect”) , you cannot define all reals one by one…
what the hell can you do at all?
defining something you cannot define?
you are talking about something you still do not understand.
but you think, you do….
but that is wrong, a unbiased look to your axioms should tell you:
you are dealing with nothing and actual infinty as if these phenomena would -in a logical way- really exist. but this is not the case.
As trolls go, at least you’re entertaining 😉
pelotom:
“Well done, you’ve shown that if I could give you an enumeration the reals, you could provide an onto function from the rationals to the reals. Unfortunately since the reals are uncountable, I can give you no such enumeration…”
Circular argument.
Dear knorke94,
Do you see the irony in how you are asking us to LIST the reals before you give us your infinite number of rationals for each real? If you pick a listing (enumeration), then you are assuming A PRIORI that the reals are countable.
This is circular reasoning, is it not? Circular reasoning tells us nothing.
What Cantor proved was that any listing of the reals is incomplete. Given any enumeration of the reals, the diagonal procedure constructs a real number which is not anywhere in that (infinite) list.
The diagonal argument is also at the heart of some of Gödel’s ideas. Are you also against Gödel’s incompleteness results?
That guy does not accept the axiom of infinity and the axiom of the empty set. I don’t think he has a particular position on logic though, since he has not provided his own set of axioms.
Oh, the irony. It hurts!
Today’s XKCD presents a new set-theoretic proof method. 😉
MrX: “So maybe I can’t declare victory, but the “heavy hitters” are unknowingly waving a white flag.”
Sometimes a white flag means: “cease fire while we
discuss things”.
Although our host opened the floor to a philosophical discussion of why some folks find Cantor’s Proof so hard to accept, he did not mince words about what he believes:
“But I will say that it is one great results of all time, in my opinion. So I am one of those who do believe in the proof, yet I think we can still discuss this belief, so please keep reading.”
OK. You don’t buy the arguments of the heavy hitters on this blog. Go back to your other comment:
“In another comment, I’m asking what mathematicians believe because they change their tune depending on if the name Cantor is uttered or not.”
If I was arguing against you in this blog, I would find that comment a bit annoying, but let’s move on.
Go look at what some of the “big guns” in the mathematical world are saying.
Currently, one of my favorite books is Stephen Hawking’s “God Created the Integers”. In the book, he discusses in chronological order the work of 21 of the greatest mathematicians that changed history (in his opinion).
He begins with: 1. Euclid, 2. Archimedes
The last five are: 17. Dedekind, 18. Cantor, 19. Lebesgue, 20. Godel, 21. Turing
According to Hawking, Cantor’s Proof can be traced back to Dedekind. A lot of the biggest guns are involved with the diagonal argument one way or another.
If I wanted to lead the charge of the “Light Brigade” into the teeth of the heavy hitters and the big guns lined up behind them, I would spend some time reconning the weakest point in their line of reasoning.
Spend some trying to figure out why they think the way they do. IMHO: The Dedekind Cut looks a bit shaky.
Jim Blair: You’re appealing to authority. I understand that most of the time, the authority is right. But scientists, mathematicians, etc. get it wrong a lot of times. Not just wrong, but colossal mistakes. In this case, there is bias by mathematicians. Also, mathematicians of the past knew it was bunk. As is the case in many fields, when one set of expert dies off, the next generation are free to implement their own ideas. That’s what happened here. It wasn’t because of some “truth” or value in Canto’s diagonal. It is still wrong, trivially so.
MrX,
Given your propensity to bash the mathematicians who believe Cantor’s Proof is valid, I thought an appeal to an independent authority like Stephen Hawking might provide a useful perspective.
I agree with you that there is a problem with Cantor’s Proof. “I don’t get it.”
Although Hawking does provide some interesting insights, I still have not figured out what it is that “I don’t get”.
I disagree with your appeal to authority:
“Also, mathematicians of the past knew it was bunk.”
Weierstrass was number sixteen on Hawking’s list of most influential mathematicians. He was also a longtime friend of Kronecker and a supportive mentor to Cantor. According to Hawking:
“In spite of Weierstrass’s efforts, Kronecker was able to block all attempts to get Cantor a mathematics professorship at Berlin.”
We can go back and forth citing authorities ad infinitum.
IMHO: I think Cantor was engaged in the time honored tradition of trying to extend “what we think we know” (the finite) into “what we know we don’t know” (the infinite).
How well he succeeded or failed is still an open question for some of us in the excluded middle.
Jim Blair: Why would you think that appeal to authority would do any good? If the proof was good, I’d accept it. It isn’t. So I reject it. That’s all there is to it.
Proof #1:
Let S be a proper subset of N.
Form a S by S matrix.
Produce an element that is in N and not in any rows of the S by S matrix.
Does this prove |N| > |S|? Of course not.
Proof #2:
Now let N be a proper subset of R.
Form a N by N matrix.
Use Cantor’s diagonal procedure to produce an element that is in R and not in the N by N matrix.
Does this prove that |R| > |N|?
What’s the difference between these proofs? There isn’t any. They’re identical. People are just hung up on the fact that the letter R is there.
Cantor’s diagonal is probably the most blatant use of circular logic I’ve ever seen. I’m amazed it was ever accepted. And you’re appealing to authority for this? Cantor only ever uses a proper subset of whatever list you give him. If Cantor’s proof were valid, it would apply to all proper subsets. It would mean that no proper subset could ever be remapped one to one.
MrX, why do mathematicians apply the diagonal argument only to show the uncountability of the real numbers and not to show the uncountability of the rational numbers? So, given a list of all rational numbers, one can construct a number by the diagonal construction which is not contained in the initial list, hence the rationals are uncountable. Why don’t they do so?
Hajduk: I wanted to be clear. Cantor’s argument does NOT fail for Q. It only fails if you try to use the diagonal technique. But my previous comment shows how you can still provide a new element.
Dear Hajduk,
The diagonal argument fails for the rationals. Indeed, the rationals are countable. It is worthwhile to spend some time trying to really understand why the rationals are countable, but the irrationals are uncountable. Why does the diagonal argument fail for the rationals (or even the integers) but not for the reals? Try it out for the integers, for fun!
The simplest way perhaps to understand the uncountability of the reals is to think that there are ‘gaps’ in the rationals. For example, the square root of 2 is a ‘gap’ in the set of rationals. This is not immediately obvious perhaps, since between any two rationals is an infinite number of other rationals. But the crucial point is that numbers like the square root of 2 are missing from the set of rationals, so there are gaps. It turns out that the gaps are uncountable! This was a fantastic realization of Cantor: the realization that the gaps in the rationals are not countable.
Dear Gandhi,
surely the diagonal argument fails for the rationals, but I wanted a concrete answer from MrX where the “proof” exactly fails. This would also show the difference between his Proof#1 and Proof#2 in his post from December 6, 2011 10:05 pm. The answer is not that it fails because the rationals are countable, if this was the only reasonthen there would really be no difference between the two proofs.
Hajduk: You said, “So, given a list of all rational numbers, one can construct a number by the diagonal construction which is not contained in the initial list, hence the rationals are uncountable. Why don’t they do so?”
The point of Cantor’s diagonal argument is to produce a NEW element not in the matrix. The technique used to produce this new element is irrelevant. So while you may think you’re being clever that any given naturals and or rational has finite digits, you miss the objective of Cantor’s “proof”. It’s the generation of a new element, not specifically the diagonal technique.
So since a proper subset of N, call this S, is the amount of digits required to represent all elements of N, then we know by definition that there are elements of S not in N. If you then form an S by S matrix, you know by definition that there are elements of N not in that matrix. You don’t need to form a diagonal to produce a new element. You already have them. But we know that we can remap S to N outside of this matrix. So Cantor’s proof is wrong.
You’re hung up on the technique to provide the new element when ANY technique that can give us a new element keeps the proof intact. I’ve done that and is enough to show the “proof” as bogus. BTW, replace N with Q. It’s all the same. The irony is pretty thick though. The very thing you thought proved you right is actually the very answer to your question.
Sorry, a correction. We know that elements of N are not in S (I had written the opposite). Also, to be clear, when you form a diagonal and flip the digits, you can potentially get an element with infinitely many digits which is not in Q. What I’m saying is that you can know there are more elements by the definition of the cardinality of the axis of the matrix. If S is a proper subset of N, then by definition there are more elements than can be found in a S by S matrix. In such a case, the diagonal technique is not needed. That there are other elements in N not in S is already a known fact.
See the difference? The failure with the rationals is usually said that the new number is not a rational. IOW, the new number is not part of the set. Problem is that you already know that there are rationals (that are part of Q) not used in the matrix regardless of what list I give you.
So Cantor’s proof MUST be bogus.
Gandhi,
Thanks for the advice.
Spending time thinking about why the rationals are countable has proven to be an interesting, although somewhat perplexing, exercise.
Gandhi Viswanathan: It does not fail for N or Q though. It’s the diagonal technique and the fact that elements of R are infinite that is tripping you up. If another technique provides a new number, then Cantor’s proof must have the same result, and yet we know that a proper subset of N can be mapped one to one with N and we know the same for Q and N.
Gandhi Viswanathan: But Cantor was wrong. The gaps always exist between a proper subset and the original set. That’s the definition of a proper subset. All Cantor did was prove that N is a proper subset of R, not that they can’t be remapped. So what good is that proof?
MrX,
> All Cantor did was prove that N is a proper subset of R, not that they can’t be remapped. So what good is that proof?
Nope, he proved that the image of any function N -> R is a proper subset of R. Big difference.
pelotom: “Nope, he proved that the image of any function N -> R is a proper subset of R. Big difference.”
No. He’s using ONE specific function and found it to not be one to one. There is absolutely NO WAY you can say he’s proved all functions are a proper subset. It’s simply impossible the way he has it set up.
MrX,
> No. He’s using ONE specific function and found it to not be one to one. There is absolutely NO WAY you can say he’s proved all functions are a proper subset. It’s simply impossible the way he has it set up.
Perhaps we’ve arrived at the root of your misunderstanding of Cantor’s proof. The proof says, “Let f be any function from N to R…” and proceeds from there. He proves something about an _arbitrary_ function from N to R, so the proof applies to _all_ such functions.
pelotom: ““Let f be any function from N to R…” and proceeds from there. He proves something about an _arbitrary_ function from N to R, so the proof applies to _all_ such functions.”
He ditches any function f I give Cantor and uses the matrix mapping instead. There’s simply no way around this fact. The matrix IS a mapping. With 1 digit, you can form two rows. With 2 digits, you can form four rows. And so on. That’s a very specific mapping between the digits and the rows. He uses this very specific mapping to enforce the digits being a proper subset of the rows. This is the circular argument part that he uses. Once he knows he’s set up a mapping where the digits are a proper subset, he then goes on to show that very fact with the diagonal.
Besides, if we took what you say as valid, then N is uncountable because you can show that there are element in N not in a proper subset of N. BTW, you really really don’t seem to have even the most basic understanding of infinity. I’m not saying this to be rude. It’s just tiring seeing the same old flawed arguments that make absolutely no sense.
The “matrix” is a device which is meant to give people an intuitive picture of the proof–clearly it has had the opposite effect on you–but it is completely unnecessary and in this case seems to be hindering your understanding. This is really a very simple proof about functions and sets, not about “matrices”. Go back and read George Kangas’ rendering of the proof. If you can’t follow the set theoretical notions, buy a book on basic set theory. Best of luck.
pelotom: The other form of the proof has the same problem. I too used the matrix to explain where the specific mapping comes from. BTW, where do you think the new element comes from anyways?
Gandhi,
If you google “algebraic number”, it looks like Wikipedia is claiming the algebraic numbers are countable and that the square root of 2 is a member of a subset called the “constructible numbers”.
The square root of 2 may not be a gap?
The square root of 2 is algebraic but not rational. It fills the gap that lies between those rationals whose square is strictly lower than 2 and those rationals whose square is strictly greater than 2. By the way, it was Dedekind’s original contruction of the reals. You can read it here:
http://www.archive.org/details/essaysintheoryof00dedeuoft
Since then there have been many other constructions:
http://en.wikipedia.org/wiki/Construction_of_the_real_numbers
Of course they’re all equivalent to each other. In practice, the properties of the reals are enough to define them up to an isomorphism. This is called the “synthetic approach” in Wikipedia.
Can each real number be described as the limit of sequence that only uses finite number of rational numbers and finite number of + – * / operations?
I meant: sequence that is defined by expression using only variable n, and finite number of rational numbers, and operations “+”, “-“, “*”, “/”.
Intuition tells me not, but I’m not sure.
Each real number is a limit of some sequence of rational numbers.
If you’re set S of sequences is restricted, so that for each s in S, a finite amount of information specifies s: then S will be at most countable. Therefore it’s set of limits will be at most countable, and so can’t include the whole (uncoutable) set of real numbers.
Your set of sequences seems to allow each member sequence to be described by a finite amount of info.
I’ve received the book Principles of Mathematical Analysis. Kinda boring/trivial so far, but I’ve only started. Here’s perhaps a simpler way to see the flaw in Cantor’s proof.
1. Assume function f from N to P(N).
2. Construct set S where x is not in S when x ∈ f(x), and x is in S when x ∉ f(x).
3. Define set T to contain all possible sets S when we don’t know f.
4. Because there are two possibilities when asking if x is in f(x), then T is a powerset of the domain of f.
5. Because of statement #4, there is a very specific injective function g from the domain of f to T that is not a bijection. (Otherwise, T would not be a powerset.)
6. This creates circular logic in that g cannot be f by definition, yet Cantor’s proof uses g as f when constructing S. f is not supposed to be the same as g. This is not a contradiction. g grabs a subset. f does not. Cantor proved g to not be one to one, not f.
QED.
Said another way, Cantor actually found out that for any infinite set A, a proper subset of A in digits is all that is necessary to represent all elements of A in base 2 or higher. This is true of N, Q, R and all other infinite sets. IOW, Cantor incorrectly treated the non one to one mapping between the digits and the rows as a difference in cardinality.
Hi Again, MrX,
I can’t believe this blog post is still garnering replies.
I can’t understand your point 3: “Define a set T to contain all possible sets S when we don’t know f.” The definition of S REQUIRES a fully defined f (which, BTW, we’re still waiting for you supply!).
If you want a more general purpose S, one that isn’t tied to one particular f, the way to do that is to make S a function of f instead. The domain of this function S, is the set of all f: X -> 2^X; the range is 2^X. The defining formula is S(f) = {x in X | x not in f(x)}. Now, for any f: X -> 2^X, we can say (by the diagonal theorem): for all x in X, f(x) != S(f). So now, for EACH f: X -> 2^X, S(f) is the proof that f is not onto 2^X (i.e., not surjective).
Perhaps your set T is the range of the above function S? I.e., T = {S(f) | f: X -> 2^X}? Then T is indeed 2^X (point 4). And we can indeed make an injective function g from domain of (any) f (i.e., from X) to T (i.e., to 2^X): the simplest way is g(x) = {x}. And sure enough, this g is not a bijection (point 5).
With that understanding of points 3, 4, & 5, point 6 makes no sense: since the function S can be applied to ANY f: X -> 2^X, we CAN apply it to g: S(g) = {x in X | x not in g(x) } = {x in X | x not in {x}} = {} (the empty set, since every x IS in {x}). So now we know that g isn’t surjective, because it’s range doesn’t include the empty set.
Now that I’ve attempted to deal with those technical points, I’ll attempt to persuade you in a more intuitive way, that the sets we call countable really are different from the ones we call uncountable.
For a “countable” set X (such as N or Q), I can identify any member X of X with a finite amount of information. E.g., for n in N, a finite string of decimal digits does the job; for m/n in Q, two such strings will suffice. There’s no upper limit on the amount of info, but no individual x needs an infinite amount of it.
On the other hand, for an “uncountable” set such as R, most elements require an infinite amount of info to identify. If I don’t provide ALL the digits in r, then I haven’t distinguished it from r’, which differs from r only in the unprovided digits.
regards,
George Kangas
I’m just saying define T as all possible values of S. There is no need to define f for us to define T since it is based on all possible values of S. There is nothing special or unusual about this. S ∈ T. Also, 2^X, by definition, is a specific mapping relative to X. This is the source of your bogus contradiction. The domain and range of f must map one to one. So then S uses the fact that X and 2^X is a mapping that is NOT one to one. That’s the problem with Cantor’s proof. If f is a one to one mapping, then the X to 2^X relationship disappears within the context of the one to one mapping. Just think of N in base 2 vs. in base 3. If you map by digit, there are more representations per digit in base 3 than in base 2. If you forget about that relationship, only then can you map one to one. If you then go back and compare base 2 and base 3 per digit, you’ll find a bogus contradiction. The first is NOT a one to one mapping (comparing by digits), but the second one is. You’re doing the same thing. Trying to use both mappings at the same time and you get a bogus contradiction.
This is what your argument comes down to. You have to decide. Do you want to use the 2^X mapping which is not one to one, or do you want to use f that is one to one? You decide. Pick ONE. Not both.
“And we can indeed make an injective function g from domain of (any) f (i.e., from X) to T (i.e., to 2^X): the simplest way is g(x) = {x}. And sure enough, this g is not a bijection (point 5).”
No, g(x) = {x} would contradict the definition of T which is a powerset. QED. g is known to be an injective function that is not a bijection. This is not a one to one mapping and is where the non one to one mapping comes from. Cantor’s proof has nothing to do with f, but rather with g.
What Cantor actually proves is that the digits are a proper subset of the rows. This is true for any given infinite set.
“On the other hand, for an “uncountable” set such as R, most elements require an infinite amount of info to identify. If I don’t provide ALL the digits in r, then I haven’t distinguished it from r’, which differs from r only in the unprovided digits.”
So what? This doesn’t prove anything. You’re just throwing out red herrings. Let me guess. You’re talking about “gaps” in Q vs R? It is SO SAD that this is what you believe. I don’t think you understand just how easy this is for me. How is it that I can still refute everyone’s objections? Why is it that no one has a valid argument? Why is it that I fully understand everything you or anyone else throws at me, and the only explanation that anyone can come up with is that somehow I really don’t understand it. Let me give you a hint. This is RIDICULOUSLY simple for me. The book I have is trivial and boring to me so far.
You want to know what the mapping between N and R is? I’ll give you one that is not, but perhaps it will clarify where everyone goes wrong. Imagine for a moment that N is a complete set. Now, normally, an infinite set has no upper bound. But suppose we include infinity to be an upper bound of N. What if I asked you to convert each element x of N to a percentage of all elements of N. IOW, what is its position in N in percentage. Well, it’s x/∞. (If you come back and say this is zero, I’ll not be impressed.) In any case, this will actually give you R. You may think that any one given element x only has finite information. True. But that’s what separates finiteness from infinity. This is what mathematicians don’t seem to get. Infinitely many naturals have infinite information.
So we need to get around that. I can divide N into two infinite proper subsets. One example is even and odd numbers. I can recursively divide those sets infinitely many times in exactly the same manner. Put these subsets into another subset V. V can now be used in the same manner as R in Cantor’s first “proof”. Note that this is equivalent to the infinite binary tree that I originally mentioned. Since V is built from elements of N, and V has the same properties of R, then |N|>|R|. And we know that if |A|>|B| and |B|>|A|, then |A|=|B|. So by that definition, |N|=|R|.
The author of this blog’s only objection was that you have to show your hand. His argument is basically to hold my arms behind my back so that I don’t do what I am doing. He made an entire new blog post about this. But does R really show its hand in Cantor’s first proof? It does not. The very notion that any two elements of R has an element in between is the very definition of not showing its hand. The entire question of N mapping to R depends on N showing its hand when arranged in one way while not showing its hand when arranged in a different way. If it can do this, then a mapping can exist. If it cannot, then there is no such mapping. Yet, N has to play by different rules? To deny this possibility from the start makes the very question of a mapping a non starter. If there is to be a one to one mapping, then N will have to be mapped in a way that makes it behave like R or vice versa. So by saying that one must show its hand and never modify it is to DEFINE N to not map one to one with R, rather than anything inherent in the axioms.
So look at what I’ve said again. It is correct. Cantor is wrong.
Did someone give you a copy of “Principles of Mathematical Analysis”, by Walter Rudin? Please repay that kindness by carefully reading this classic textbook. What you describe as “kinda boring/trivial” is what coherent mathematical communication actually looks like, and what you have yet to learn. You can’t convey coherent thoughts without coherent communication. Your arguments confuse the types (element of set, set, mappings between sets, input to mapping, output of mapping…) of the objects under discussion.
“define T as all possible values of S” ??
That’s not a coherent definition, MrX. You have to say HOW “all possible values of S” are to be combined into one object. Here are some possibilities, from best to worst (in my opinion):
1) T is a function, with f: x -> 2^X as input, and T(f) = {x in X | x not in f(x)} as output. I called this S(f) in my previous reply. I like this one because for each f: X -> 2^X, this function provides T(f) as proof that f isn’t surjective.
2) T is the set of possible S’s, i.e. the range of the function described in item 1. But, since any subset of X is f(x) (for some f and some x), we would just have T = 2^X which isn’t very interesting.
3) T is the union of the set of possible S’s, i.e. the union of the set described in item 2, i.e, the union of 2^X. But that’s just X, which is even less interesting.
Perhaps you have something else in mind?
“2^X, by definition, is a specific mapping relative to X” ??
2^X is not a mapping from anything to anything. What is the input to this “mapping”, and what is the output? What 2^X is, is the powerset (set of all subsets) of X. An equivalent (up to isomorphism) way to read it, is the set of all functions from X to the set 2 = {0, 1}. So then each member of 2^X is a mapping of X, but 2^X itself is not.
“This is the source of your bogus contradiction.” ??
I never made a proof by contradiction, bogus or otherwise. I just show that each f: X -> 2^X is not onto 2^X, since {x in X | x not in f(x)} is not in the range of f. Got it? Good.
“the domain and range of f must map one to one” ??
Whatever gave you that idea? Diagonalization works on ANY f: X -> 2^X, not just an injective one.
“So then S uses the fact that X and 2^X is a mapping that is NOT one to one.” ??
The phrase “X and 2^X” does not describe any single object in ZF, so it doesn’t describe a mapping of any kind. But S doesn’t “use” any of this incoherent nonsense; all that S does (where S = {x in X | x not in f(x)}) is show that this one particular f: X -> 2^X is not one to one (because for every x in X, f(x) != S).
“You want to know what the mapping between N and R is?”
Yes! We ALL want to know it, so we can all IMMEDIATELY provide the proof that it’s not onto R.
“I’ll give you one that is not…”
Oh, well. When will you give us one that IS? In time for Christmas would be nice!
“I can divide N into two…”
What you describe is scheme for representing each element n of N, by which division (and division of division, etc.) that it’s in. Okay, fine, base 2 is such a scheme. Notice that each n can be specified by finitely many choices (e.g. in base 2, each n has finitely many nonzero digits).
“V can be used in the same manner as R in Cantor’s first “proof”. …and V has the same properties as R.”
No. Here’s the key difference between V and R: a typical element r in R requires infinitely many digits to specify. That’s why diagonalization can be applied to f: N -> R, but cannot be applied to f : N -> N. If we attempted to apply diagonalization to f: N -> N, the resulting “number” would have infinitely many nonzero digits, and so it wouldn’t be a (natural) number.
“The author of this blog’s only objection was that you have to show your hand. His argument basically is to hold my arms behind my back so that I don’t do what I am doing.”
Cantor’s proof can be stated in ZF, i.e. it doesn’t use the axiom of choice which would put it in ZFC.
In ZF (unlike in ZFC), the only way to prove some kind of object exists, is to axiomatically construct an object of that kind. So if a surjective f: N -> R can be proven to exist in ZF, the proof must START with the construction of such an f. That’s why “you have show your hand”.
AFTER you construct f, you’ll prove it’s surjective. Then, since diagonalization (simply and easily) proves that this same f is not surjective, ZF will collapse into inconsistency. The Cantor cult will be forever vanquished!
Before that can happen, MrX, you will have to learn to communicate in the coherent style that bores you so much in Rudin’s book. But then you will find yourself thinking coherently as well, which will probably dissolve your objections to Cantor’s proof.
Happy Holidays!
GK
George Kangas: I bought the book. And it is boring.
“You have to say HOW “all possible values of S” are to be combined into one object”.
What are you talking about? The construction of S doesn’t explain from what set it exists. I fill in that gap. I then go on to show how it is a powerset. It is the set of all subsets of the range of f. This was all explained.
“2) T is the set of possible S’s, i.e. the range of the function described in item 1.”
Yes on the first part. As to the second part, what is item 1? The first option you listed? The range of f: X -> 2^X? That is not well defined. 2^X is not mapped one to one with X. But then you go looking for a one to one mapping and then attempt to check against the original non one to one mapping. Your complaint that I’m not being precise is EXACTLY my complaint against this entire discussion and Cantor’s proof. Mathematicians toss out infinity without having it well defined often confusing cardinality for mapping.
“But, since any subset of X is f(x) (for some f and some x), we would just have T = 2^X which isn’t very interesting.”
Not interesting? What does that even mean? If that’s a “mathematical term”, then you caught me. I’m not familiar with it. I personally find it very interesting. T = 2^X is exactly right. It cannot map to X by it’s definition not being X, but rather 2^X. Hence, Cantor’s proof is bogus.
“2^X is not a mapping from anything to anything.”
More non well-defined technobabble. 2^X has X in it. It is definitely a mapping.
“What is the input to this “mapping”, and what is the output?”
The input is X. The output is something that maps to X within a “larger” set. IOW, the ouput is a proper subset of 2^X, but where the output also maps one to one with X.
“So then each member of 2^X is a mapping of X, but 2^X itself is not.”
Congratulations on contradicting yourself, yet not. This is the very contradiction that Cantor got mixed up about as well. It’s unfortunate that by the very existence of your confusion, you cannot understand said confusion that is the flaw in Cantor’s argument. Allow me to try anyhow. A mapping that is not one to one is still a mapping. This is what you’re actually saying when you say that “2^X is not”. That’s it. That’s the flaw. Cantor checks f against this non-one-to-one mapping. So what? f isn’t supposed to be non-one to one anyways.
“I just show that each f: X -> 2^X is not onto 2^X, since {x in X | x not in f(x)} is not in the range of f. Got it? Good.”
But you do no such thing. T = 2^X according to the definition of S. So T cannot be one to one with X since the definition of T does not allow it. You don’t seem to understand that the only way for f to exist is if T maps one to one with X (the domain maps one to one with the range through the use of f). But through the construction of S, you use a definition that is NOT one to one with f (or X), call this g. This says absolutely nothing about if f exists or not. It only speaks about the function g that maps f to T.
” “the domain and range of f must map one to one” ?? Whatever gave you that idea?”
It’s not a one to one mapping otherwise. IOW, any other use of f betrays the original assumption and the proof becomes bogus.
“Diagonalization works on ANY f: X -> 2^X, not just an injective one.”
No, it does not. It doesn’t work in any way, shape or form. It works on g, a mapping from f to T. g is by definition not one to one. And this is the conclusion of Cantor’s diagonal. This says nothing about f.
“The phrase “X and 2^X” does not describe any single object in ZF, so it doesn’t describe a mapping of any kind.”
Of course it does. I call it function g. But 2^X is a set that has elements that are not mapped to elements of X. This is a non-one-to-one mapping. The question is if there exists a DIFFERENT mapping that IS one to one. But the moronic part of the S construction is that T is 2^Y where Y is the range of f. It is effectively 2^X if f is a one to one mapping. So it checks against the non-one-to-one mapping to see if it’s valid. That is completely moronic.
I already explained why it’s stupid by using N represented in base 2 and base 3. This is the bane of mathematicians who believe in Cantor’s argument. They see the flaw in one case, but turn a blind eye when it exists in another case just because they’re biased at its “beauty”.
“all that S does (where S = {x in X | x not in f(x)}) is show that this one particular f: X -> 2^X is not one to one (because for every x in X, f(x) != S).”
Again, it does no such thing. In constructing S, you are also creating a set in which S exists. I’m pointing out that this set T is defined as 2^X according to the construction of S. So in creating S, you’re using a mapping function g from f to T that is not one to one. So it has nothing to do with f at all. The fact that any function f has the same result… this alone should be indication that Cantor’s “proof” is flawed and has nothing to do with f.
“”You want to know what the mapping between N and R is?” Yes! We ALL want to know it, so we can all IMMEDIATELY provide the proof that it’s not onto R. “I’ll give you one that is not…” Oh, well. When will you give us one that IS? In time for Christmas would be nice!”
I provided one afterwards. I wanted to first show where mathematicians get it wrong when discussing infinity and natural numbers.
“No. Here’s the key difference between V and R: a typical element r in R requires infinitely many digits to specify.”
How is that different? Each element of V, where each element is itself a set, has infinitely many elements.
“If we attempted to apply diagonalization to f: N -> N, the resulting “number” would have infinitely many nonzero digits, and so it wouldn’t be a (natural) number.”
Too bad. That excuse doesn’t work here. We’re using V, not N. No one said elements of V are natural numbers. I only said that the union of the elements of V is N.
“The Cantor cult will be forever vanquished! Before that can happen, MrX, you will have to learn to communicate in the coherent style that bores you so much in Rudin’s book.”
But this is MY COMPLAINT against Cantor’s diagonal argument and his first argument. The definition of infinity is not well defined at all.
What’s even more ridiculous is that you have NO CLUE about what infinity is. Again, I’m not saying to be rude or anything like that. It’s that there is no other way to let you know that you simply don’t understand the topic you’re trying to talk about. You don’t even accept that X and 2^X has a mapping. Seriously, this kind of nonsense is not helping.
The irony is that Cantor starts out with a function g: A -> B that is NOT one to one between A and B. He sets it up and proves this fact though we already knew it because that’s the definition of g anyhow. He then jumps to the conclusion that there is no function f: A -> B that IS one to one. He believes that g is not a specific mapping. But the reality is that g can never be one to one by its very definition, but it is not all functions. That’s the problem.
Hi, MrX,
Posting comments on this blog is pretty inconvenient. The columns are too narrow. Maybe my browser (Safari) is being dumb, but it won’t cut & paste for me, so I have to cut & paste by hand (i.e., retype) to respond to you point by point. Also, I think we’re the only dicussers left in this discussion. So I invite you to email me: . Put “MrX” in the subject.
Rudin’s book is good; you showed good taste in selecting it. It’s not really a set theory book, that’s just covered in a perfunctory way as a foundation for real analysis in the rest of the book. It gets more interesting when it starts dealing with functions of real numbers. Do some of the exercises. Try to absorb the explicit, unconfused style.
“The construction of S doesn’t explain from what set it exists. I fill in that gap.”
If X and f: X -> 2^X have been defined, then S = {x in X | x not in f(x)} is a fully explicit, axiomatic definition in ZF. There is no gap to be filled.
“2) T is the set of all possible S’s, i.e. the range of the function described in item 1” (quoting myself).
The function described in item 1 is T: (X -> 2^X) -> 2^X. I mean the range of this T, not the range of f.
You seem to agree that this range is 2^X (i.e., that the function T is surjective), and that’s the meaning you intend for T. We’ll go with that. My opinion, that the function T in my item 1 is more interesting than the set T = 2^X in item 2, is just an opinion. You’re welcome to ignore it.
“Mathematicians toss out infinity without having it well defined often confusing cardinality for mapping.”
ZF has an “axiom of infinity”, which basically says that the set N of natural numbers (defined by induction) exists. Then the definition of “infinite” is just this: If there exists injective f: N -> X, then X is infinite. According to ZF, that’s all there is. If you think that’s too simple, then find an inconsistency. If you can give us surjective f: N -> R, that would be just such an inconsistency. Mathematicians would then have to reexamine their notions of infinity.
Cardinality is defined by the existence of a mapping. |X| = |Y| if there exists bijective f: X -> Y. That’s not confusion, that’s the definition.
“2^X is not a mapping from anything to anything.” (me again)
Before you can coherently communicate mathematics, you need to learn the distinctions between the data types under discussion. A mapping is a thing which consumes an input and produces an output. 2^X is not such a thing. You could say that “2^_”, i.e. the powerset operator is such a thing. If X is it’s input, then 2^X is its output. So 2^X is one possible output of this mapping, but it is not itself a mapping.
If you’re still confused, let’s suppose X = {a, b}. Then 2^X = { {}, {a}, {b}, {a, b} }. How would you use { {}, {a}, {b}, {a, b} } as a map? Give examples of inputs with resulting outputs.
“T = 2^X according to the definition of S. So T cannot be one to one with X since the definition of T does not allow it.”
Do you realize, that this statement actually AGREES with the conclusion of the diagonal theorem (from my earliest post, I think): that for any set X, |X| 2^N ? If not, then |N| < |2^N|.
As soon as you agree that |N| R. That will establish that |N| <= |R|. Then we have |N| < |2^N| <= |R|, and we'll be done.
ciao,
George
I’ll email you, but I wanted to leave the first response here.
George Kangas: “If X and f: X -> 2^X have been defined, then S = {x in X | x not in f(x)} is a fully explicit, axiomatic definition in ZF.”
I disagree that it’s explicit. The set that S is in is not the range of f(x) since S is found to not be in that range anyhow. So what is the set that S is a member of? We know it’s from the powerset. However, the construction of S tells us exactly from what set it is built. The construction of S defines a specific subset A ⊂ T where S ∉ A and T is the powerset of the range of f(x). And when I say powerset, I’m saying that A, being a proper subset to T, has a very specific mapping to the range of f(x). A ⊂ range of f (and I’ll show why below). This is all a very specific setup where there is actually no contradiction at all.
I’ll give you an analogy. Suppose you want to find out if it’s possible to drive from Canada to Argentina with a car and nothing else. You figure out the maximum amount of gas that any single car on the market can handle and calculate the best miles/km per gallon/litre and prove that you’ll run out of gas before you get anywhere near Argentina. QED.
That’s Cantor’s proof in a nutshell. The setup is arbitrary. The contradiction is self-imposed. Just like my analogy can just stop at gas stations, Cantor’s argument can also look more closely and see that the self-imposed contradiction is exactly self-imposed. IOW, it’s not a contradiction that is valid in proofs by contradiction. Much like matching digits of N by base 2 and base 3 to prove that |base 3| > |base 2|. Why doesn’t this contradiction work? Because you don’t need to use it. It’s self-imposed. BTW, this is EXACTLY Cantor’s flaw. It’s a difference in base.
Back to the problem at hand. You take the range of f(x) and create YET ANOTHER POWERSET on top of the powerset that f(x) is supposed to map to. Here’s where your bogus contradiction comes from. Each element of f(x) is mapped to x in the original powerset construction. This is how you can ask if x is in f(x) in the first place. This mapping is unfortunately no longer one to one when you ask if it’s in f(x) or not. You’re asking f to be that one to one mapping. So in asking if x is in f(x) or not, you’re arbitrarily bringing back the non one to one mapping A and saying that S is not in it. But A is not the range of f.
What this means is that you’re now using a proper subset of the domain of f. You’re using a proper subset of N as the indexes into f. So S is indeed in the range of f, but only if you don’t use a proper subset of the original domain of f.
The mindboggling this about Cantor’s proof is that you must do away with the notions of proper subsets. N is not always N when there’s a specific mapping in place. N is its own proper subset. Cantor does not verify that he’s not actually using a proper subset of N. Just saying it’s countable is not enough.
The above is correct. Look it over as many times as you need. But I assure it is 100% correct. No matter what list I give you, you can only use a proper subset of N of it. Forget R. Forget Q. Forget N. You use a proper subset of N of any list I give you. And you cannot prove otherwise. Every mathematician simply handwaves it away. Too bad. That doesn’t make the flaw disappear.
“T: (X -> 2^X) -> 2^X”
No. Because you ask if x is in f(x) or not, then you get a powerset of 2^X.
“T: (X -> 2^X) -> 2^X^X”
Since you’re using the domain of f to index into the range of f (this is the mapping I talked about earlier between members of f(x) and x), then you effectively get this:
“T: (subset-of-X -> X) -> 2^X”
That’s what you get.
That’s your flaw.
Let me ask you this. Suppose you assume the existence of f that maps X to 2^X. What is the range if I use a proper subset of X for the domain of f?
Now, you don’t have to agree with me just yet. I’d be happy if you could just answer what would happen if Cantor is actually doing this? Would the proof hold up?
Heck, I think Cantor just proved that the powerset of digits of N is N itself. Right there, he’s actually proven the OPPOSITE of what he thought he was proving. The powerset of a proper subset of N would require infinite sequences. But because N has elements that aren’t mapped to, it can indeed take care of those situations. And once you’ve proven that sets with numbers with infinitely many digits can map to N, it’s a done deal. Cantor actually proved that |N| = |R|.
Dear MrX: Do you understand the strict inequality,
?
Gandhi: yes, but it’s a question. Not a fact.
George Kangas: “A mapping is a thing which consumes an input and produces an output. 2^X is not such a thing.”
Your statement cannot hold up. 2^X has X in it. This means there is a use of X when defining 2^X. As such, there is a mapping in there somewhere. All I’m doing is showing where that mapping exists. If there was no mapping, you could say that Y is the powerset of X and that would be it. You could no longer check if x was in f(x) or not because Y has no use of X in any specific way.
Your statement is another place where mathematicians say there is no mapping, yet there is, helping cause the bogus contradiction.
“let’s suppose X = {a, b}. Then 2^X = { {}, {a}, {b}, {a, b} }. How would you use { {}, {a}, {b}, {a, b} } as a map?”
OMG! JUST WOW!!!
The mapping is between a’s in the domain and a’s in the elements of the range.
2^X = { {0,0}, {1,0}, {0,1}, {1, 1} }
The above is equivalent to your 2^X set. The mapping is one to one with your definition of 2^X. But now you can see that the elements of X map one to one with the elements of the elements of 2^X. When you ask if x is in f(x) or not, you bring back this mapping. If you’ll note, X has two elements, 2^X has four. Even in infinity, the definition of the powerset will have this non-one-to-one mapping between X and 2^X because the one to one mapping is between the elements of X and the elements of the elements of 2^X.
What this means is that Cantor is checking that the one to one mapping exists in two places at once. He wants it between the elements of X and the elements of the elements of 2^X when you check if x is in f(x) or not. And then ALSO checks it between the elements of X and the elements of 2^X when building S. But in 2^X, the mapping between the elements of 2^X and the elements of the elements of 2^X are NOT one to one by definition. So you’re going to find a contradiction every time. Not because f can’t exist. But because you’re using two contradictory mappings at once.
Mathematicians cannot let go of the original mapping.
One last comment,
George Kangas:
““T = 2^X according to the definition of S. So T cannot be one to one with X since the definition of T does not allow it.”
Do you realize, that this statement actually AGREES with the conclusion of the diagonal theorem (from my earliest post, I think): that for any set X, |X| 2^N ? If not, then |N| < |2^N|."
Yeah, but it's the original definition of the powerset. It's like saying you have a one to one mapping f, but it doesn't map with the non-one-to-one mapping g of the definition of the powerset. Big deal. It's not supposed to map to T like that. It's supposed to map to a transformed version of T. Otherwise, the one to one mapping will never exist. It's like comparing base 2 and base 3. If you don't allow one of the sets to be transformed and mapped differently, you'll never have a one to one mapping and will always find a contradiction. Funny how the base 2 and base 3 scenario never sinks in. Again, just because Cantor's name is used, mathematicians throw the book out the window.
Correction: You’re right that g(x) = {x} would be a proper subset of T. What I meant is that g cannot be used to map to T. IOW, yes, you say that no matter what f you use, it won’t map to 2^X. But it’s g you’re talking about, not f. g(f(x)) is not f(x). That’s not a contradiction. That’s expected because g is intentionally defined to be an injection and not a bijection. This proves nothing about f.
MrX,
FYI: Quoting someone is not equivalent to citing an authority. Being curious about what someone thinks and quoting them is not an implicit endorsement that I agree with them.
Out of curiosity, I downloaded a copy of Rudin’s book.
The notion of a “proper subset” as defined by Rudin is at best ambiguous. Currently, I am also inclined to argue that it is also ambivalent.
IMHO: You are right about Cantor’s Diagonal Argument, it is flawed. Here is wishing you luck in developing a more compelling counter argument.
There are countable many Turing Machines and uncountable many decision problems (or functions from N to {True,False}).
If Cantor is wrong, wouldn’t the existence of undecidable problems be in doubt also?
Azevedo,
Yes. It is almost the same argument.
Maybe some problems, but not all. For example, the deceiver version of the Halting problem would remain unaffected. But the diagonal version would no longer hold.
As far as Cantor, it seems that in the construction of S, when you ask if x is in f(x), there are two possible values. Call this new function g(x). This means that for each x, you have two possible values. Hence the domain is a proper subset of the codomain because of g, not because of f. That’s why it doesn’t matter what f is. f could very well could be one to one. But the mapping applied afterwards when asking if x is in f(x) changes the codomain. From some recent discussions, I’ve been told that producing one out of two possible values for each input is not a mapping (albeit a mapping that is not one to one). How can this be when it’s the smoking gun used in the “proof”?
If you look at the codomain vs. the range when you consider ‘g(x) = x is in f(x)’, you’ll see that the cardinality of the codomain doubles at every x and so g cannot be one to one by definition. What makes the codomain double is asking if x is in f(x) which has two possible values of true or false. It has nothing to do with f specifically and that’s the true reason why it doesn’t matter what f really is in the “proof”.
Oops, the blog erased my email address from that post. I’ll try again, without brackets this time. kangas@math.ku.edu
In case that doesn’t work: kangas at math dot ku dot edu
Reading my post from the blog, I see that the blog has mangled my test in several places. Email would be a lot easier.
Is there a simple way to reconcile Cantor’s notion of equinumerous with the Euclidean notion of equidistant?
>The names are selected to reflect what they believe: Uncounts believe that the reals are uncountable and Counts that the reals are countable.
Great blog. I think there are those that are Uncounts and that do not believe in Cantor’s Proof. Believing Cantor’s Proof is flawed doesn’t mean one discards Cantor’s intuition that the reals are “different”.
MrX: I have read what you wrote, as well as what others wrote. I have also thought of the infinite binary tree before and asked, isn’t this an enumeration of the real numbers? Thanks to the discussion on this blog, I now understand that is incorrect.
This was the breakthrough in my reasoning.
It’s completely true that the nodes and paths in the infinite binary tree are countable. Each node in the tree corresponds to a unique number, which is encoded by the path we take from the root to reach that node.
So if you give me a number, like 3, or 1000, or 7204283949, I can tell you exactly which node in the tree corresponds to the number you gave me. I can draw out the tree as much as needed, and then physically trace out a path, starting from the root and terminating on the node that precisely equals your number. I can respond with something like, “The node for your number is in row X of the tree, Y nodes from the left.” Since the nodes are enumerated and countable, I can also tell you exactly the number of the node that corresponds to the number you gave me. Maybe the number you gave me is node #84095, for example.
But then let’s suppose you gave me pi, which is a number that goes on forever… has infinite digits with no repeating pattern. Can I do the same as before?
No.
I will start tracing through the tree from the top, but I will NEVER TERMINATE on one precise node as I did before. I will have to go on forever, infinitely, just like the number pi itself. I cannot point to a node that equals pi, because that would mean I can reach that node using a path with FINITE steps from the root. BUT pi has INFINITE digits.
Of course, I can get arbitrarily close to the number pi, by just going deeper into the tree. But I will never finish my journey on a node that exactly equals pi. If you gave me pi, you would be waiting forever for my answer.
And that was my breakthrough: the sharp dichotomy between giving you an answer in a finite amount of time (and being able to point to a specific node), versus running forever and never being able to stop on one node. Or put another way: In countably infinite sets, such as the integers or rationals, the entire set is infinite, but every element within the set is finite. In uncountably infinite sets, such as the reals, the entire set is infinite, AND elements within the set can themselves be infinite in extent.
@Mike, I’ve already accounted for everything you have mentioned. The problem of infinite digits is exactly what Cantor used to construct his pseudo-proof. That’s the very flaw. He assumes that this difference of finite length vs. infinite length can never be mapped to each other (this is the exact thing he’s supposed to prove BTW and is why it’s circular reasoning) and then proceeds to show how naturals have finite length and reals don’t by only using a subset of the reals. No matter what list you think you give him, he only uses a subset.
Don’t get me wrong, the length issue is at the core of proving that reals are countable.
There is a way out. The length is infinite, not the element. The element that is made up of infinite digits is still finite. So we can map one (one = finite BTW) natural element to one infinite sequence that can map to a real.
What I want to do is not map one specific node to one infinite path. I want to show that there is a surjection from the nodes to the infinite paths.
1. Take a set S of infinite paths.
2. Build an infinite path starting at the root node.
3. Once you reach a node that is not used by any path in S, then you also have an infinite path not in S. Every subsequent node will also be different (ie. known to not be used by any path in S) by definition of the infinite tree.
4. This means we don’t need to store the entire path as the elements in S. We can instead store the tail portion that is different from all other elements in S meaning that all elements of S are disjoint sets. If we want to reconstruct the entire path of any element of S, we simply follow upwards in the tree and there is only one path possible by definition.
5. We define set T where for each element/path e in S, we use the topmost node (of the tail) of e as the element in T creating a bijection between T and S.
6. When R is defined in the same way as S (call this U), then we also have a set V that can be defined in the same manner as T above, but that maps one to one with R, or rather U.
7. Define the set of all nodes N as the union of V (IOW, all the nodes in all elements of V) and is countable since these nodes map one to one with the nodes of the infinite binary tree which is known to be countable.
8. Since V ⊂ N and there is a bijection between U and V, then U ⊂ N.
9. Since U = R, then R ⊂ N.
10. If N ⊂ R and R ⊂ N, then |R| = |N|.
QED.
Hi, first of all I am not a mathematician (I’m a life scientist! ha). But math topics are something I sometimes think about/read about for fun.
MrX–I’m trying to understand your argument. Let’s let S be the set of all infinite paths that begin from the root and all go through the left child of the root. None of the paths in S go through the right child of the root. What is the composition of the set T for this set S?
@Mike: “Let’s let S be the set of all infinite paths that begin from the root and all go through the left child of the root. What is the composition of the set T for this set S?”
There are many ways to compose T. Suppose you have a path that stays always to the left. Then you’d have infinitely many left nodes. In this example, I’ll use even numbers for right children (except for 0 that is the root node) and odd numbers are left children. The numbers are taken sequentially per row. For the path that goes through nodes 0,1,3,7,15,31… (all left children), put that list in S as a single element and put 0, the root node, in T. If another path is 0,1,3,8,17,35… (XLLRLL…) Put {8,17,35…} in S and 8 in T since 8 is the first node not already in S. Keep going through all the paths and keep putting the first node in the path that isn’t already in S. There are many ways to construct it. 0,1,4,10,22… (XLRRR…), we’d put {4,10,22…} in S and 4 in T. But you don’t have to do it sequentially. In fact, these examples are just to visualize. The point is that it’s possible to define R in such a way that all elements are disjoint sets. Then just take the first element of each sub-path in S to define T. A sub-path is the tail end of the infinite path in question.
So far, we have
S = {{0,1,3,7,15,31,…},{8,17,35…},{4,10,22…},…}
T = {0, 8, 4, …}
As you can see, all elements (aka sub-paths) in S are disjoint. They share no common node with any other sub-path in S, yet are fully descriptive of their full path because there is only one way up from their first node.
In essence, the continuum problem can be reworded as such:
Is it possible to describe R so that it only contains disjoint sets as elements? And where elements of the disjoint sets can only contain elements of N. If so, then a surjection from N to R exists.
I came up with this because it exactly represents the Dedekind principle stated in statement 10 If A ⊂ B and B ⊂ A, then |A| = |B|. Said another way. If you have set A and B; then if you can describe A in terms of disjoint sets that only contain elements of B, then A ⊂ B.
We start with R = the set of all paths. Each path is defined as the set of nodes it goes through. No one has any problem with this. Then I define another set S based on this earlier description where we remove nodes from each path to create disjoint sets.
Thus R ⊂ N.
Thanks MrX, I have a much better idea of your meaning now.
Actually, after thinking about this some more, I don’t think an infinite path is a problem per se. For example, the infinite set consisting of {pi, 2pi, 3pi, 4pi, …} has every element with infinite digits, yet the cardinality of this set is very obviously the same cardinality as the natural numbers N. (A real number with infinite digits = an infinite path in the binary tree.)
The question we are concerned about is really the number of infinite-length paths. Obviously there are an infinite number of infinite-length paths, but is this infinity the same as N or different?
Going back to your proposal, you said “there are many ways to compose T.” The example you gave was just listing random paths one after another, but I was wondering if you could be more specific by explaining a systematic way to compose T that is guaranteed to represent every and all infinite-length paths in the set S that I gave you?
@Mike: “The example you gave was just listing random paths one after another, but I was wondering if you could be more specific by explaining a systematic way to compose T that is guaranteed to represent every and all infinite-length paths in the set S that I gave you?”
I don’t need to build it. I just need to prove it exists. And that’s trivial since I only need to prove that infinite disjoint sets built from paths that go through all nodes cannot allow more paths. See below.
I’ll give you a method, but again, this is for visualization only.
Start where U has as elements their full path (ie. all nodes that it traverses).
Set W, S and T are initially empty.
For each element x in U, do the following:
1. Pick a node y in x that is also not in W.
2. Define an element z that is x without the nodes above y. It does include y however.
3. Add z to S.
4. Add top most node in z to T.
5. Add the union of z to W.
W will then be N and T will be a proper subset of N and there will also be a bijection between T and S and between S and U.
Suppose we believe that |R| > |N| and W will be N with elements of U not mapped in S. This means that it’s possible that even with W accounting for all nodes in the tree, that you can still produce a path not in S. But if you can only create paths with nodes that all exist in other paths, then you cannot create a new path since for any given node, you know that all nodes from that one to the root are identical since there is only one way up as each node only has one parent. Since it is impossible to differ from all other paths, it must be a path that already exists in S, thus contradicting our assumption. Therefore S must be R. And since there is a bijection between S and T, then |R| = |N|.
Actually, if you just take the infinite tree and go to the first node t that is unused, create a path with that node t. Put t in T and put t and all nodes below it (the nodes chosen don’t matter as you’re guaranteed they’re not used by any other path and hence is a disjoint set by definition) in S as a single element. Mark all these nodes as used. Put the full path in S. Do this for all nodes. If all nodes are accounted for since they are countable, is it possible to create an infinite path not in S? No matter what path you pick, at any given node along that path, you have an identical path to the root with an element in S. It’s trivially obvious that it’s impossible to create a new path. So S = R and it’s mapped to a subset of N.
Hi MrX, I request that you consider the statement: “This sentence is false.” Is it true? False? Or neither? Your opinion here will be relevant to what follows.
First of all, I appreciate that there is a certain intuition (at least, as much as we mortals can have about the concept of infinity) to your claim that all infinite-length paths are accounted for by your method. However, I also have an intuition that your enumeration covers only the computable reals, not the set of all reals. The computable reals consist of real numbers that can be calculated to arbitrary accuracy using finite time and space. Pi, despite being irrational and transcendental, is actually a computable real because we know of formulas for computing the Nth digit of pi. One of Alan Turing’s results was that there are UNcomputable real numbers: these are even stranger than pi and cannot be expressed using the finite language of math, even though the number represents a finite quantity. Interestingly, the computable reals, like pi, are enumerable and countable, but the UNcomputable reals (and therefore, the set of all reals) are uncountable (according to conventional wisdom, of course). Since I am not a mathematician, I just read/think about math topics as a fun hobby, I am not equipped to formally show that your method enumerates only the computable reals. It is my intuition.
Instead, I would like to analyze your enumeration. You have proposed a method to map every infinite-length path to the nodes of the tree in a 1-to-1 fashion. Here is my analysis:
1. If your method is successful, then every possible infinite-length path is mapped to one, unique node of the tree.
2. The nodes are enumerable, starting from the root (1), then going to the first level of the tree (2, 3), then the second level (4, 5, 6, 7), and so on.
3. Therefore, every infinite-length path maps to a positive integer in a 1-to-1 correspondence. Each path is a sequence of left (L) and right (R) steps from the root. So we can list the paths as follows:
1 LLRRLRL…
2 LLLRLRR…
3 RLRLLRR…
4 RRRLLRR…
etc.
4. Let us examine the path described by the L/R sequence along the diagonal. You must be thinking, “Oh no, not a diagonal!” But hear me out, I’d like to see what you think about my analysis. In this example, the path along the diagonal will be LLRL…
5. For this path, change all L’s to R, and all R’s to L. This gives RRLR… In other words, the Nth step of this path is obtained by taking the Nth step of the Nth path, and changing it to R if it was L, or to L if it was R.
6. The path RRLR… must be in our list, since we assumed every infinite-length path was listed. Therefore, it maps to a positive integer. Call it X. Therefore, our list contains the following:
X RRLR…
7. Question: what is the Xth step of this path? Is it R or is it L? If it is R, then it should be L due to how the path was formed. But if it is L, then it should be R. This presents a problem.
The fact that the Xth step of the path cannot be L or R is similar to the statement, “This sentence is false,” which is not true or false. Such a statement is referred to as undecidable within the ZFC axioms. If you think you have a way to decide it, you’re right, but you would have to adopt a new set of axioms (but then there would be new statements that are undecidable in your new set of axioms). The concepts of uncountable (set theory), undecidable (logic theory), and uncomputable (computational complexity theory) are all related.
Since you will probably disagree with my analysis of your enumeration, which step(s) do you disagree with? I numbered them for your convenience of referring to them.
@Mike: “Let us examine the path described by the L/R sequence along the diagonal.”
That doesn’t affect my proof. The L’s and R’s aren’t opposites except for the first level below the root node. IOW, you can have L’s in your new number and L’s in a particular row and they can still be different. The only way to be the same is if the current node and all those above it are the same.
Also, your list only contains a subset of all the reals in S. This is the Cantor flaw. Your enumeration of 1 to N is not my enumeration. My enumeration is where this sequence is NOT one to one with the digits. I’m using a subset of the total nodes. You said it yourself. Root node is 1. Second row is 2,3. Third row is 4,5,6,7 and so on. But I don’t map each node to each real. I map a subset of all nodes to the reals. I create disjoint sets. These disjoint sets each contain infinitely many nodes and I pick the first one for the set that I map to the reals.
So when you try and make a square infinite grid, it no longer uses my non-one-to-one relationship between the digits and enumeration.
Call M the set of all nodes. And T the nodes that map one to one with the reals as in my previous examples. Also set P which is the set of positions going down any infinite path. Allow me to demonstrate the relationship between all of these.
T ⊂ M
P ⊂ M
P ⊂ T
In my enumeration, the digits are a subset of T where T is my enumeration. You use a square grid and redefine my enumeration in a way that removes rows from the list. And then you find such a number that you just removed and claim victory. Well, too bad. It’s not my enumeration and what you found is completely expected.
Here’s a better question for you. In base 10 or base 2 strings (or whatever base you wish), prove that there is a bijection between the digits and the rows of N. And then try it with R. You won’t be able to prove it. This is the flaw in your argument. It’s not true that there is a bijection between the digits and the rows for the any infinite set including the reals.
THIS LAST PARAGRAPH is what Cantor proved.
Read that last sentence again. Think about it. He proved that the reals do not have a bijection between the digits and the rows. He proved there were more rows than digits. Again, this is EXACTLY my claim in the paragraph above. It is also true of N. So if you create a list of naturals, the digits will map to a subset of the rows. We can even calculate the exact ratio.
What’s funny is that mathematicians will say, “We already know that the digits of N and the rows of N are countable.” Sure, but I’m talking about the mapping between the digits and the rows. They will not have a one to one mapping in that specific scenario. N is its own subset. There is nothing wrong with using such a relationship. And such a relationship exist with the digits and rows of N. All you need to do is see that the diagonal of N is all 0’s. By definition, this means that there is a surjection from the rows to the digits.
The only enumeration that has a one to one mapping between the digits and rows is the infinite identity matrix. But Cantor’s grid fails in such a scenario because he can no longer flip digits and there is no way to represent reals in such a format.
Let me state it once more. The only complete list of any infinite set is one where its digits are a proper subset of the rows. If you change this in any way, you’re no longer using the list I gave you. So if you use a square grid, that’s not my enumeration.
You were probably thinking that even if the L’s can indicate different paths, then an L compared with an R is definitely different which is all you care about. But here’s the thing. There are rows missing from your list. I’ll prove it again.
Take your new number created by the diagonal. Go down the infinite tree and tell me which node has not been used by another real. You can’t. Therefore it is in my list. But not in yours.
“However, I also have an intuition that your enumeration covers only the computable reals, not the set of all reals.”
No. My proof doesn’t care about computable or not computable. It only cares that it has 0’s and 1’s or left and right.
“One of Alan Turing’s results was that there are UNcomputable real numbers: these are even stranger than pi and cannot be expressed using the finite language of math, even though the number represents a finite quantity.”
There is no digit at position infinity. Repeat that. There is no digit at position infinity. Every single digit is at a finite position.
I’ve said it before and I’ll say it again, if Cantor’s proof succeeds, then it must fail. It is a self-defeating proof that automatically proves itself wrong upon success.
@Mike:
You wanted to know what step I disagreed with specifically.
In step 5,
“In other words, the Nth step of this path is obtained by taking the Nth step of the Nth path”
I don’t use a bijection between the digits and the rows in my enumeration as can be seen by the infinite binary tree. Multiple nodes per row precludes it from having one node per row. The length of a path is a proper subset of all the nodes (and the length of a path is also a proper subset of T). So any use of a square infinite grid is not my enumeration. You are removing rows from my list if you cut short the rows to create a bijection between the digits and the rows. In my list, there is a surjection (and non-bijection) from the rows to the digits as required by all infinite sets (except the infinite identity matrix which is the only way to get a bijection).
FLAW IN CANTOR’S PROOF
Here’s an alternate way to describe the flaw in Cantor’s diagonal.
For Cantor’s proof to hold, he must prove that there is no surjection from the rows of N to the digits of N. We know this to be false because we need only look at the diagonal which is all 0’s. This means that we can map all rows until we hit a 1 on the diagonal to that digit. Multiple rows for each digit. Note that we don’t care what mapping is used by Cantor. We only care at this point that a surjection from the rows of N to its digits exists. And I’ve just described one.
The point is that Cantor simply proved that there is a surjection from the rows of R to its digits. No disagreement there. But that’s the flaw. The same property is true of N, yet there is no difference in cardinality between the rows of N and the digits of N since we know outside of Cantor’s grid that the rows of N and the digits of N are both countable.
That’s a fatal blow to Cantor’s proof. A surjection of the rows to the digits does not imply a difference in cardinality. What’s worse, the surjection is EXPECTED in both N and R. It’s a known fact.
In the past, trying to explain this, mathematicians would say, “Yes, it doesn’t map one to one. That’s what we’re trying to show.” So you can see how difficult it is to explain the flaw. The surjection does exist, but all infinite sets must have such a surjection including N. So if a surjection with N doesn’t prove that the rows of N have a different cardinality than the digits of N, then it doesn’t prove anything with respect to cardinality between the rows of R and its digits.
Cantor must prove that there is no such surjection for N which is ridiculous because I’ve just described one such surjection at the top of this comment. This is a required step because if a surjection does exist between the rows of N and its digits, and it does, then this means it is not enough to prove a difference in cardinality. But even if he were to prove the case with N (which is impossible, but even so), it still wouldn’t be enough to prove that a surjection implies a difference in cardinality when it comes to R. Lack of proof to the contrary does not imply proof positive.
—-
Let’s consider 4 infinite sets A, B, C and D.
A is the rows of the naturals.
B is the columns of the digits of the naturals when put in a grid.
C is the rows of the reals.
D is the columns of the digits of the reals when put in a grid.
We know that B ⊂ A and D ⊂ C. We know there is a bijection between A and D. So I’m going to transpose the AB grid so that the A and D sets are at the top of the grid. It’s the same set N, so no problems. They match up perfectly one to one if we were to overlap these grids.
Along the rows, we have three sets.
1. B
2. N (both A and D) This is Cantor’s square grid.
3. C The reals
Within this grid, we know that B ⊂ N ⊂ C
Cantor wants us to believe that N ⊂ C is proof of a difference in cardinality, but not B ⊂ N?
That’s the problem. Cantor is rejecting the notion that an infinite set is its own subset.
Here’s a MUCH easier question to understand.
Why does a surjection from the rows of R to its digits imply a difference in cardinality?
It has no such implication on N. So why on R? We all know the logarithmic relationship between rows and digits in N. That’s proof that a surjection exists. Yet cardinality is the same. But for R, the rules change? Why?
Hi MrX, I just have 1 question. Maybe I wasn’t understanding your mapping correctly, so I want to clarify it. Are you proposing a method to map every infinite-length path to one node each, or to a set of nodes?
Short answer is both, but I’m not proposing a “method” per se.
I’m saying that there exists a set S that can describe all reals where each element is a disjoint set. Each disjoint set contains infinitely many nodes.
So that set doesn’t have a mapping in as much as it IS the set of reals. You can reconstruct each and every path because there is only one way up the tree. These disjoint sets are the tail end of the infinite path. So they do contain infinitely many nodes. If you take the topmost node, then you can continue up to the root node because there is only one way up.
To define set T, which has only one node per element, it’s like this:
For each element x of S, T contains the first element of the disjoint set x.
So f(x) = x(1) is the mapping to form T from S.
Set S contains infinitely many nodes in each element.
Set T contains one node for each element.
If every infinite-length path can be designated by one node (the set you call T), then we can list the paths just like we can list the nodes. Do you agree or disagree with the previous sentence, and why?
List the nodes in T? Sure.
The infinite-length paths can be listed too, right?
For each element in T, you can retrieve the associated element in S and reconstruct the full path, sure.
That all makes sense. Countable is just a synonym for “listable”.
So can we list the infinite-length paths as below, where we give them arbitrary numbers 1, 2, 3… ? It should be possible if there is a bijection between infinite-length paths and N.
1. LLRLRLRLLLR…
2. LRRRLRLLRRL…
3. RRRRRLRRLL…
4. LLLRLRLRLRL…
etc.
So far so good?
Sure, but note that there is a surjection from the rows you’re listing to their “digits” L/R. You can’t use a square infinite grid like what Cantor uses, otherwise you’re not using my list.
Two sets–whether finite or infinite–are the same size if and only if a bijection (1-to-1 correspondence) exists between them.
So does a bijection exist between N and the set of infinite-length paths or not? If a bijection exists, then they can be listed 1, 2, 3… which will list every infinite L/R sequence exactly once, by the definition of a bijection.
I have no problem with anything you’ve said in your last comment. But my list has a surjection from the rows to the digits. Any deviation from this is not my list. There is nothing in this that contradicts anything in your last comment.
If your list has a surjection from rows to the digits, then that means some digits (infinite-length) paths are represented by more than 1 row. Am I understanding you correctly?
What are “digits (infinite-length) paths” mean? Multiple rows map to the same digit if you want to word it that way, yes.
But there is a bijection between T and the paths, right?
Yes.
And we agreed we can list the nodes in T. Call them T.1, T.2, T.3… etc.
Is this your list?
T.1: LLLRLRLRLRLLL…
T.2: LRRRRLRRLLR…
T.3: RRRLLLRRLRL…
etc., where every T.X is associated with 1 infinite-length path, X being a positive integer, and all infinite-length paths are listed.
Yes.
That list, which is yours, looks a lot like this list,
1: LLLRLRLRLRLLL…
2: LRRRRLRRLLR…
3: RRRLLLRRLRL…
etc.
which is mine. All I did was remove the “T.” because T.X is just an identifier that can be replaced by X. In other words, there is a bijection between T and N. Do you agree or disagree and why?
I never disagreed with that part.
So your list is the same as mine? I thought you said they were different.
No. I said you’re not using my list if you use Cantor’s grid. It seems you’re trying to get me to say it’s the same list and then do some operations that would alter it. That’s the Cantor flaw.
Let’s use a finite grid instead to demonstrate the flaw. Suppose I give you a grid that is 4×16. 4 columns wide and 16 rows. You list 16 rows and ask me if that’s my list. I say yes. You then take a diagonal on the top 4×4 area, flip the digits and say this new number is not in my list. In the finite grid, it is clearly in my list if all the rows are unique. In the infinite grid, your diagonal doesn’t work for the same reason. I have a surjection from the rows to the digits. So when you take a diagonal, the number you create IS in my list because you only used a subset of my list. This is why I said it’s not my list. Because it’s impossible to use my entire list when you create a diagonal. The diagonal only crosses a subset of the entire grid.
That was Cantor’s argument. He said you could generate a new number from your list that was supposedly not in your list.
That has never been my argument.
I’m saying generate a path along the diagonal by flipping L’s to R and R’s to L. It doesn’t matter if certain paths are listed more than once, so a surjection is fine. The new path we just formed must be listed at least once. Let X denote the row where this path appears first. What is the Xth step of this path–is it L or R?
You’re using the exact same argument. And there are no paths listed more than once.
If you flip L’s to R’s and vice versa, you cannot traverse the entire list because I have a surjection from the rows to the columns of L/R digits.
So your new path… guess what? It’s in my list.
“Let X denote the row where this path appears first. What is the Xth step of this path–is it L or R?”
Like I said, there is a surjection from the rows to the digits. So there are X’s (aka rows) that map to a digit you already used.
“Like I said, there is a surjection from the rows to the digits. So there are X’s (aka rows) that map to a digit you already used.”
I’m having trouble understanding this. Can you explain further and/or provide a tangible example?
Also, I know it’s in your list. I even said where it is. What is the Xth step of this path though?
By the way, your 4×16 grid finite example doesn’t work with my argument. There are only 4 digits, but there are 16 rows, so the Xth digit is undefined for rows 5-16.
“so the Xth digit is undefined for rows 5-16.”
CONGRATULATIONS!!! In a surjection with infinite sets, the same thing happens. Certain Xth digit do not exist for certain rows. Hence why the diagonal path cannot work.
But with infinite-length paths, the Xth digit (if number) or Xth step (if L or R) must be an actual value, not left undefined like in your finite example, for any positive integer X.
“But with infinite-length paths, the Xth digit (if number) or Xth step (if L or R) must be an actual value, not left undefined like in your finite example, for any positive integer X.”
My digits are not numbered against any set N. They are numbered against the floor(log(X)).
Any deviation from this is not my list. So yeah, you can add 1 to the position of the row and digit. That’s not my list.
Interesting. I simply do not agree that “Certain Xth digit do not exist for certain rows” if a row describes an infinite-length path, regardless of how you “number the digits”. Clearly you believe differently. That’s OK–we must each arrive at our own beliefs in our own way. Since we will apparently never agree on this point, let us go our separate ways.
Regardless, I found this discussion fascinating, and it was very satisfying to pinpoint the precise source of our differing views, which was this point just raised. Thank you.
I agree. I never would have imagined this would be it.
@Mike: Wanted to add one last response to your last comment.
“I simply do not agree that “Certain Xth digit do not exist for certain rows” if a row describes an infinite-length path, regardless of how you “number the digits”. Clearly you believe differently.”
If R is not countable, then you are correct. But if R is countable, then what Cantor found out about R also applies to N and my assertions about Xth digit not existing for certain rows are true since this is true of R which is a countable set as found by Cantor’s diagonal.
This is the source of the circular logic. This is the ONE AND ONLY TIME I’ve ever been able to comment on it. At no other time has anyone even wanted to look at this. And I’m fairly certain no one will.
Clarification: The phrase “as found by Cantor’s diagonal” was in relation to “Xth digit not existing for certain rows”.
If your list has a surjection from rows to the digits, then that means some digits (infinite-length) paths are represented by more than 1 row. Am I understanding you correctly?
At last we’ve arrived at the crux of MrX’s peculiar belief system. “Certain Xth digit do not exist for certain rows.” I can’t possibly imagine what kind of notion of the meaning of an infinite sequence could lead to that statement.
My list is defined as a surjection to the digits. So you’re simply not using my surjective mapping when you discard it and decide to use a bijective mapping and is no longer the same list I gave you. It’s actually Cantor’s argument applied to the naturals. I don’t believe it’s possible to list any infinite set where it’s digits are a bijection with its rows except with the infinite identity matrix. So if this is true of N, then it can’t possible be used as a technique to prove a difference in cardinality.
@rjlipton: You wanted to know why Counts don’t believe in Cantor’s argument. Well, here’s a simple description.
We Counts believe that all infinite sets, whether N, Q or R, have a surjection from the elements of the set to the columns of digits required to describe these elements and that no bijection is possible is said scenario (but remove the relationship between digits and rows and yes, there can be a bijection). The one exception being the infinite identity grid that has a bijection since it can be transposed and as an aside is proof that the digits of N are infinite and countable.
We believe that Cantor proved this relationship between a set and its digits for R and nothing more. That this is ONE specific mapping.
This does not imply a difference in cardinality since the digits of N will always be a proper subset (non-bijective) of the countable set it describes unless it is the infinite identity grid.
One other point of contention is that if I give a list where the rows have a surjection, that Cantor can just traverse the rows and digits sequentially with total disregard to the surjection that defines my list. We Counts do not accept this. We believe that Cantor’s argument applies to the naturals as well and that a surjection exists for all infinite lists between the rows and columns of digits and no bijection between rows and digits is possible within such a list (but outside the list, yes). There is no opposite diagonal technique, but simply looking at the diagonal and it not being all 1’s is proof enough that multiple rows (up until it is a 1 in that column) can map to each column creating a surjection. There is no list of naturals where this is not true except for the infinite identity matrix.
Since there is always a surjection from the rows to the digits in any given list with the naturals and never a bijection, this means that using a square infinite grid implies a proper subset of N for the rows when creating the diagonal in Cantor’s argument wrt the reals.
The point of contention is the assumption that a set A defined as a surjection from another set B can be traversed sequentially in its entirety when only using set B as elements that map to A. The assumption is that they are both countable and are sequentially traversable. But they’re using the other set B that defines A. There is only an injection. An injection cannot possibly map to all elements of the other set even if traversed sequentially.
One example I give is that for each element x in R, I will swap it with another row that has all zero’s except for the digit index that equals the row index. This will create the identity matrix and you will never use all the elements in my list. So sequentially traversing a list is not enough to guarantee a bijection between two countable sets that are specifically defined as being surjective.
In any case, Cantor’s argument applied to N is identical to what I describe in the last two paragraphs. Not that the diagonal is to show a surjection. With the naturals, just looking at the diagonal and it not being all 1’s is enough to show a surjection.
Greetings, MrX!
I hope you’ve had a good year, since we last corresponded. I’m ready if you are, to waste some more time on this. You can reply by email, as well as here.
I read with some interest your latest exchange with Mike (Hi, Mike!). Like me (a year ago), Mike understands the *simple* claim and proof attributed to Cantor. Like me, he takes on the challenge of trying to untangle your dizzyingly complicated misunderstandings.
I’ll try (yet again!) to discard that complicated baggage, this time by removing that claim and proof from the language of set theory. I’ll transplant it to a language about countably-infinite strings of L’s and R’s.
Dirt-Simple Claim: For any countably-infinite list, consisting of countably-infinite strings of L’s and R’s, there exists a countably-infinite string of L’s and R’s which is *not* in that list.
Dirt-Simple Proof: The complement of the diagonal of the list differs from every string in the list, therefore it’s not in the list.
I hope that the claim and proof above are too simple to be misunderstood or disbelieved by you; the next step is to realize that Cantor’s claim and proof are *precisely equivalent* to this.
Cheers!
George Kangas
Dear George, although this may be true, as I understand it, MrX is claiming that there is a string in the list that coincides with your counterexample in all letters except may be the last one, which does not exists by the definition of infinite sequence. So our counterexample is not a real counterexample, since it cannot be constructed.
Dear MrX, why not to be a bit more constructive, and agree with others that indeed Cantor constructed a number not in the list, but then show that there is a number in the list that is not more distant from the constructed counterexample than 0.1111… from 1.00… both being equal to 1 . That may be not exactly the construction you had in mind, but would probably be more convincing for others to accept.
@George: I’m doing well. Thank you. I still have your last email marked unread. I didn’t think we had much more to say at the time and this topic tends to absorb a lot of time (though I do enjoy the discussions). So I left it there until I could read up some more on other but related mathematical topics.
To see circular logic, let us take the opposite view that Cantor does. Because he assumes a difference in cardinality, he arrives at said conclusion. And if he assumed a difference in cardinality is impossible, Cantor’s proof shows that R is countable.
So let us assume that we know R is countable. Not as part of Cantor’s assumption in his argument, but rather that we can never conclude that infinite sets are not countable even after the conclusion of Cantor’s argument. Keeping Cantor’s argument the same, what does this imply?
It means that the mapping between the rows of a countable set (the only kind possible) and its digits is a surjection. That this is true of N, Q and R.
It’s a rather unusual turn of history that different cardinalities were not rejected long ago. If it had been rejected, Cantor’s argument would be a very nice proof showing the mapping between the elements of an infinite set and its digits is a surjection. It would also show that my “swap” example from earlier is true. This is where I swap each element of N with another element that is composed of all 0’s except for a 1 at the n’th position where n is the row index. As one can see from this example, you can go through the rows sequentially, but never traverse all rows. This is what the diagonal construction implies, but everyone handwaves away.
What’s really happening is a comparison between two representations where one is restricted compared to the other. The diagonal implies a mapping to the identity matrix. The identity matrix is the ONLY representation of N where the digits and rows have a bijection. But it’s not binary. The reals are in binary, but not the infinite identity matrix required by the diagonal.
Said another way, suppose you do believe in Cantor, then does this not imply that I must give you a list where the rows of N have a surjection to the digits? Yet, you never allow such a construction. You only use the identity matrix which is square and known to never map to R. Heck, it doesn’t map to N in binary either. But we don’t assume the identity matrix has a different cardinality than N represented in binary, do we? So why does it work with R? It’s absurd.
@MrX:
The *actual* claim and proof made by Cantor is far simpler than the complicated mess that you keep talking about. That’s why I restated it in terms of lists of strings of L’s and R’s.
You keep talking about maps “from the rows to the digits” (and the way you use “digit” seems to mean column), and all such talk is utterly irrelevant. The only map under discussion, is *the simplest possible* map which that the matrix could be used to represent: the *input* is just some natural number n, the *output* is just the nth row. And just forget about the damn columns, because they play *no* part whatsoever!
The only claim being made, is that any such list (of strings of L’s and R’s) must be incomplete. For the simple reason, that the diagonal complement differs from each string in the list. You do understand this simple claim and proof, yes? Well, that’s all there is to understand! Cantor’s claim and proof is *precisely equivalent* to this!
@George: No. My claims are easy to follow. You just ignore them over and over. This is what everyone does that doesn’t want to see the truth. In your very first reply, you fall right back into your groove. Deny deny deny.
It’s simple. What cantor found out about R is true of N as wall. Deal with it. If you’re unwilling to look at it from this perspective, then end of discussion.
@George: “And just forget about the damn columns, because they play *no* part whatsoever!”
Really? So how do you create the diagonal then?
Look George, I told you before you don’t understand infinity. So it’s perhaps best if you give it up. It’s clear that you have no idea what you’re talking about. I’ve tried to be polite in the past. Perhaps being blunt will make more of an impact and make you realize you’re in over your head.
MrX:
“No. My claims are easy to follow. You just ignore them over and over. This is what everyone does that doesn’t want to see the truth. In your very first reply, you fall right back into your groove. Deny deny deny.”
Textbook projection! No one on this epically long comment thread has been able to follow your crazy claims, MrX. And you are the one falling repeatedly into your own demented groove no matter how many well-meaning people try to show you the simple truth of this proof.
Then why has not one person been able to put a hole in my arguments? NOT ONE. Every single objection has been silly or something that Cantor himself uses.
I know with 100% certainty that my arguments are correct. No one has been able to put a hole in it. So the obvious tactic is to try and change what my arguments are.
Look, when the best objection in this entire thread is that because all digits are finite, that I can only map to Q, you know you’ve entered loony town. That is the ABSOLUTE BEST objection put forward so far and it’s completely nuts.
It’s impossible to point out the flaw in a proof you don’t understand. No one here understands what you’re saying, because you use ambiguous, nonstandard terminology.
On the other hand we do know what you are *claiming* to have proved, and since Cantor has furnished a very lucid proof of its impossibility which we all understand, the obvious conclusion is that you are wrong, whatever you may be trying to say with your impenetrable screeds.
You are correct. You believe in Cantor so conclusively that you are unwilling to listen to any alternative. Thank you for being honest about it at least.
Nice strawman–it’s not about belief. We are trying in good faith to understand you and failing.
“A proof is a repeatable experiment in persuasion.” — Jim Horning
You have persuaded exactly one person — yourself. Maybe you’re content with that.
@pelotom: I love that quote!
@MrX:
Here’s what happens, if we attempt to perform Cantor’s diagonalization on N (the natural numbers). I’ll use binary notation, and the obvious in-order enumeration. Also, the string of 0’s and 1’s extend leftward, instead of rightward, from the binary point (analogous to “decimal point”).
…0000000000000000000000001
…0000000000000000000000010
…0000000000000000000000011
…0000000000000000000000100
etc.
The diagonal (which starts at the upper right, then moves downward and leftward) is: …0000000000000000000011. Thus the diagonal complement is …111111111111111100.
This diagonal complement is indeed not one of the numbers in the enumeration (because of the mechanics of diagonalization, which you fully understand). But that does NOT disqualify my enumeration, for the simple reason that …11111111111111111100 is not a natural number! It’s not finite, and you (Mr. Xpert on infinity) know that every natural number is finite.
@George: The point of the diagonal is to find a number not in the list. Match by digits and you can do it. Suppose we have a list N represented in binary. Take the first row and swap it with a number that has all 0’s except for a 1 on the diagonal. Still the same set. Just using a different representation for the first number. The second number, do the same thing. Again, same set. Just using a different representation for the second number. And so on. You will only ever get a proper subset of the original list. You can do this for ANY list N in binary.
You completely missed the point of the diagonal. It is not the specific technique that is important. It is the fact that a number not in the list is found. Well, we can do the same with N.
@MrX:
“The point of the diagonal is to find a number not in the list.”
Yes, that’s exactly the point of diagonalization: to construct a number not in the list, and thus to show that the list is incomplete. The “number” that diagonalization constructed in this case wasn’t actually a number, so its absence does *not* make the list incomplete.
I agree, that diagonalization isn’t necessarily the only way to construct a number not in the list. So go ahead and carry out your own evil plan, with swapping and such, and construct for us this brand new natural number, that appears nowhere in the sequence which I listed: 1, 10, 11, 100, 101, 110, 111, 1000… (that’s the sequence of ALL natural numbers, using binary notation). So, MrX: reveal to us all this brand new natural number, which is somehow absent from the sequence of all natural numbers, and achieve instant fame!
WOW! I just told you. At no point can you reach any natural number that doesn’t have all zero’s and a 1 on the diagonal.
Small question for something I’m not understanding. Theoretically you could represent all the reals as infantesimally small denominations of each Natural number and each negative of the Naturals. Assume that there is the same number of objects in every infinite set. With that you could attempt to map the natural numbers to the reals, but you wouldn’t make it from 0-1, because and infinite number of 1/Infinite sized objects would exist in the infinite-sized subset of Reals: 0-1. If they have the same number of objects you couldn’t make it to 1, and there would be no bijection from the objects 1-infinity.
However this appears to create a contridiction. If you have an infinite number of infantetesimally small objects you would in fact reach 1, as Infinite/Infinite would be 1, leaving an infinite number of 1/Infinite objects, or Infinite/Infinite number of objects to map 1-2 and so on ad infinitum, yes? This means that the moment you apply infinite size to the sets rather than moving incrementally you immediately map every object.
Am I looking at something wrong here, or does this actually look like an infinity-esque uncertainty principle to anyone else? Where as you look at scope of a set (for exampe Reals vs Naturals) infinity cannot apply, but when you enforce infinite size to the set, scope become irrelevent?
This is of cause useless, but I will try to give a different view on MrX construction. One path on the tree can be encoded as binary sequence – left – ‘0’, right ‘1’. We are going to use the Cantor assumption that infinite sequence can imaginably written down. Now to make things a little bit easier to work or harder to confront with, we are going to use random enumeration of paths, or the same of binary sequence. Cantor argument says that there exist a real number r (its infinite, say binary, string representation) and a *finite* position n, such that there are no, in our terms, path, or binary string, coinciding with truncated to n digits number r (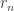
) in its binary (path) representation. Lets work things out. We start with our list of random paths (binary strings), and select only those of them, that coincide with 
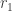. Since we had infinite paths, half of them is still infinite. Than we repeat – at step k we have infinite number of paths, coinciding with 
. Moving to step 
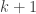we have a half infinite = infinite number of paths coinciding with 
. Therefore, there is no finite k satisfying Cantor arguments. Contradiction.
I know that I’m unspeakable crank. If you believe there are uncountable many reals, by the above construction you see that there are at most countable different reals, all the rest are divided into countably many sets of measure 0. Kind of 0.1111… = 1.000… tautologies. Or may be there is something I do not see? Of cause we can talk about what means random. It means I do not care how you will enumerate the list, any mapping will work fine. That probably means that the topology of real numbers destroys to power sets argument, where all sets are disconnected. But don’t worry, I’m crank, and my arguments are trisection.
Let the following list represent the adjacency matrix for an infinitely large clique:
1. 01111111…….
2.101111111……
3.110111111…..
4.111011111…..
The confusing thing about the diagonal argument is that it creates an unlisted element of the list that looks like it should be on the list.
Forgot to indicate the list continues indefinietly:
5. 111101111………..
……………………………
n. nth element is 0. the rest are 1’s.
…………………………..
If I may interject… what you have listed is a “stencil” that goes over the list of reals that is provided to Cantor. Wherever there are 0’s, Cantor takes the digit that is at the same location in the list of reals and flips it from 0 to 1 or vice versa.
What if I used this same stencil (flipped horizontally) over a list of naturals represented in binary? However, I then swap each natural with the natural that is the opposite of the current row. So if you have ….11111101, I swap the same row in the list of naturals with the element that is 10. I do this for all rows.
Once you do this, you find that not all naturals are traversed by the diagonal. That there are infinitely many naturals left over.
So Cantor’s argument applies to the naturals as well. Therefore it cannot be used as a technique to find a difference in cardinality.
MrX,
The observation I was making is that it is possible to create an infinite list of strings of 0’s and 1’s following the well defined pattern of an adjancy matrix of a infinite clique.
You don’t need the diagonal argument to see there are alot of missing strings.
If someone uses the diagonal argument, they are only pointing out that the string of all 1’s is missing. One of many missing strings.
Dear Dick,
The Lebesgue Measure is well defined in the Count world. It is the fraction of numbers represented by the binary strings in well ordered sequence normalized by the range of the interval one defines measure on. This is similar to the probability concept defined by Edwin Thompson Jaynes in Probability Theory: The Logic of Science. So if one have single point its fraction is 0, if there are finite number of points their fraction is 0, if there countable number of points one can speak about finite fraction. It has the same problem as entropy for continuous variable, but if one fixes precision everything is well defined. Than one can speak about limit in terms of precision, something like principal value of an integral.
I do not know anything about Baire Category Theorem, but the notion of dense set naturally appears in Count world when one goes to the limit of infinite sequences. The same as the notion of open set and the boundary. I guess It is more convenient to work with current definition of reals – the proofs are shorter. But sometimes it may lead to confusion, or conceptual difficulties. I guess it is dual representation of the same concept, so it should be used as a power, not as a confrontation.
Reblogged this on maha's place.
Does the diagonal argument fall apart if you construct your enumeration starting from the first and last rows simultaneously?
For instance:
s(1) 0,0,0,0,0,0,…
s(2) 1,1,1,1,1,1,…
s(3) 0,1,0,1,0,1,…
s(4) 1,0,1,0,1,0,…
… …
s(N-3) 0,1,0,1,0,1,…
s(N-2) 1,0,1,0,1,0,…
s(N-1) 0,0,0,0,0,0,…
s(N) 1,1,1,1,1,1,…
Building a unique s using the diagonal argument starting at s(1) will produce 1,0,1,1,.. which exactly matches the diagonal produced at the other end, s(N). The nth digit of s will always match the nth digit of s(N-n-1). Therefore Cantor’s argument is not sufficient to ensure that s will be unique.
The order in which you constructed the enumeration doesn’t matter; diagonalization is applied to the complete enumeration.
Also note, that there is no last row. After row N, there’s row N + 1. For every N.
Cheers,
George Kangas
Well in that case could those terms extend into the interior like this? I guess my choice to use the label N was arbitrary.
… …
(N+3) 0,1,0,1,0,1,….
s(N+2) 1,0,1,0,1,0,….
s(N+1) 0,0,0,0,0,0,….
s(N) 1,1,1,1,1,1,….
Or can there not be an infinite number of terms between some s(i) and another s(j)?
Cantor’s theory fails because there is no completed infinity.
According to set theory the figure
1
2, 1
3, 2, 1
…
contains an infinite number of elements, namely all natural numbers.
No row of the figure contains an infinite number of elements.
According to mathematics, the figure is an inclusion-monotonic sequence of finite rows. That means: Every union of finite rows is contained in one of the unioned rows. (The principle of construction shows, that this property is independent of the number of finite rows. Otherwise there would be a first finite row that does not contain all elements of its predecessors.) If the contents of the figure is a fixed quantity, then this fixed quantity is in one of its rows. Therefore the idea of the natural numbers being a fixed quantity can be excluded.
Regards, WM
Every union of a FINITE set of rows, is equal to one of the rows. The union of any INFINITE set of those rows, will be the set of all natural numbers.
I don’t know whether the natural numbers are a “fixed quantity”, since I don’t know how you define that term. But the objects of conventional math (Zermelo-Frankel set theory, or ZF) are called “sets”, and they do include infinite sets, unions of infinite sets, and the set of natural numbers.
If the infinity-infested ZF is inconsistent, the inconsistency has remained undiscovered for about a century now. All the more exciting, WM, if you could manage to find one!
According to mathematics for every finite union of rows there is a row containing more natural numbers.
According to set theory however there is a union of all rows which contains more natural numbers than are contained in any of its finite rows. That is a fixed quantity.
As a consequence the natural numbers must be dispersed over many rows.
This is in contradiction with mathematics for finite and infinite sets of rows:
Proof. If infinitely many rows are required to contain all natural numbers, then at least two rows are required to contain more than each of them. Contradiction.
The inconsistency of ZF is a psychological problem: A block in the brains of its adherents. I have experienced this with hundreds of students who have no problem to understand the above argument.
Regards, WM
Hi WM. Long ago, I was a grad student in math. My studies included ZF.
“According to mathematics for every finite union of rows there is a row containing more natural numbers.”
Yes, just go “the next row” after the longest row in the FINITE union.
If the union is infinite: then there is NO longest row, and NO row containing more natural numbers.
“According to set theory however there is a union of all rows which contains more natural numbers than are contained in any of its finite rows.”
Yes again, the union of all rows (or the union of any infinite set of rows) will be equal to the set of all real numbers, and thus greater than any row.
“That is a fixed quantity.”
And I still don’t know what “fixed quantity” means, or why it matters.
“If infinitely many rows are required to contain all natural numbers, …”
Infinitely many row are indeed, required, so you conclude…
“…then at least two rows are required to contain more than each of them.”
This simply doesn’t follow. It’s only the FINITE unions of rows, that are contained in longer rows.
“The inconsistency of ZF is a psychological problem: A block in the brains of its adherents.”
If you come up with a FORMALLY CORRECT proof that ZF is inconsistent, you could verify it by a computer program! You could bypass the blocked brains of us adherents.
This would require that you first learn the rules of the game (first order logic, axioms and inference rules of ZF). Good luck!
Well, if we apply the same technique as Cantor, then we can say that any given row has finite elements. So any given union will have each element of that set map to a row in N. The largest such row will be a superset of the given union. If this were not the case, then you would need a row that was infinite and we know that is not possible. As such, all unions taken from N must be finite. This means N is not infinite. We know this is nonsense. But for some reason, the diagonal construction does the exact same thing as I mentioned in the previous sentences yet it’s taken as gospel when applied on R.
Hi George, I am a professor of mathematics. My lessons include set theory. My source book will probably cover the stuff that you have learnt about ZF:
https://www.hs-augsburg.de/~mueckenh/Transfinity/Transfinity/pdf
Let me explain what “fixed quantity” means and why it is crucial.
It is a number, A, that is in trichotomy with all cardinal numbers including natural numbers n.
It matters because of simple mathematics: If there is the claim that A rows (containing less than A elements each) are required to contain A elements, then there must be at least two rows containing together more than each of them. Contradiction.
Your statement “That simply doesn’t follow” is simply counterfactual. Every computer program will confirm that required rows are required. But you cannot find any row that is required.
In an inclusion monotonic sequence of finite rows it is impossible to have A elements distributed over A rows. That’s mathematics. All the rest is a chimera.
Regards, WM
Concerning your request for a formal proof: Mathematics has many languages, one of them is FOPL+ZFC. Nobody is forced to apply it, since it has not the magic power of final decision attrributed to it by its adherents, in particular the translation of mathematical ideas into its formulas is a matter of arbirtrariness.
The common mathematical language is well suited for simple problems like the current one:
If aleph_0 is a number in trichotomy with all cardinal numbers including all natural numbers, then the natural numbers cannot be dispersed over aleph_0 segments, each of which is containing less than aleph_0 elements. That is mathematically impossible by the inclusion monotony of the infinite sequence of segments.
There is not the least necessity to translate this in any other language in order to have it understood by people with some mathematical knowledge.
Regards, WM
To Mr. X: “Well, if we apply the same technique as Cantor, then we can say that any given row has finite elements. So any given union will have each element of that set map to a row in N.” Of course. But there are infinitely many finite rows and infinitely many finite natural numbers. Infinity in mathematics, so called potential infinity, means that there is no upper bound. Cantor’s finished infinity means that there is, in his own words, a quantity larger than every natural number. That is wrong. At least it is incompatible with mathematics, namely inclusion monotony of the infinite sequence of finite rows.
There is no last n and no last row. But there is only an “up to every row”. I know that this is not so easy to understand as Cantor’s finished infinity, because the latter resembles something finished.
Regards, WM
You call those who believe the proof Uncounts and those that do not Counts, and Uncounts believe that the reals are uncountable and Counts that the reals are countable.
However, you also appear to assume that anyone who accepts that the reals are uncountable must also believe the notion that the reals constitute a “bigger” infinity than natural numbers, and that there are “more” real numbers than natural numbers is logically untenable.
But I accept that the reals are uncountable, but I do not accept that the the reals constitute a “bigger” infinity than natural numbers. The reason I say this is because the diagonal proof is a proof where any presumed enumeration of real numbers must be in the same language system as these real numbers in order for the diagonal number to be definable.
Of course if you want to indulge in special Platonist pleading that numbers somehow “exist” independently of any definition, in which case you can also assume that there “exist” numbers for which there is no definition – which is all very convenient if you want to get a result that there “exist” “more” such “numbers” than definable numbers. But I only accept a logical analysis of definitions which do not depend on any Platonist assumptions of “existence” independent of any definition.
While Lebesgue measure and the Baire category theorem might show that the reals are uncountable, they do not show that the reals constitute some sort of “bigger” infinity.
The notion that the reals constitute some sort of “bigger” infinity comes only from one specific argument, which involves different levels of language, and which goes like this:
If every real number could be expressed in some language as some finite combination of symbols, then we could easily have a method of matching the natural numbers to these combinations of symbols. All that is required is an alphabetical style ordering of all the symbols used to define real numbers (in the same way as a, b, c … is the order for the English alphabet), and then you simply list them in the same way as you would order the words in a dictionary. And if you could list them, you can obviously attach natural numbers to every item in the list. But this would contradict the Diagonal argument, so there must be real numbers that cannot have any finite representation.
The obvious flaw in that argument is that it forces the enumeration of the reals to be in a different language system (a meta-language) from the real numbers of the list, where every combination of symbols that defines a real number in that system is simply an object in that meta-language, and which has no inherent numerical value in that meta-language. Hence that meta-language has no method of generating a diagonal number from that enumeration. The laughable thing about that argument is that it introduces different levels of language while at the same time completely refusing to analyze whether that introduction of different levels of language might affect the overall proof.
Obviously, I am only able to give a brief synopsis in the above, but you can read a fully detailed account at http://www.jamesrmeyer.com/infinite/diagonal-proof.html.