Isomorphism Is Where It’s At
Isomorphism at the SODA 2014 conference
Ronald Read and Derek Corneil are Canadian mathematicians and computer scientists. Read earned a PhD in Mathematics from the University of London in 1959, while Corneil was one of the inaugural PhD’s in the University of Toronto’s Department of Computer Science. Read is also an accomplished musician and composer—indeed our photo comes from his entry with a sheet-music publisher in England—and here is a music-themed paper. Corneil became Chair at UT DCS and has done much liaison work with Canadian IT companies and international education. Together they wrote a survey paper in the 1977 first volume of the Journal of Graph Theory titled “The Graph Isomorphism Disease.”
Today Ken and I would like to take issue with one of the words in their title. No, not “disease,” but rather: “graph.”
The graph isomorphism (GI) problem itself has a long history, and already did in the 1970s. The computational problem is to determine whether two given adjacency matrices (or edge lists) of graphs in fact represent the same graph, and has considerable practical importance. The theoretical problem is whether GI has a polynomial-time algorithm; GI is in 
Happily this disease has been manifesting itself in different forms that recently seem amenable to being “cured” by real progress. The list of accepted papers to the upcoming SODA 2014 conference has several instances:
- Lattice Isomorphism: a paper by Ishay Haviv and Oded Regev.
- Order-Type Isomorphism: a paper by Greg Aloupis, John Iacono, Stefan Langerman, Özgür Özkan, adding Stefanie Wuhrer.
- Robust Graph Isomorphism, an approximation concept developed by Ryan O’Donnell, John Wright, Chenggang Wu, and Yuan Zhou.
None of these directly targets GI or its main spinoff, group isomorphism. Still, the range of interesting and applicable isomorphism-type problems is expanding in ways we appreciate. But first some words about the originals.
Graph and Group Isomorphism
Unfortunately, one of us—that is I, Dick—have spent more hours then I care to admit, working on these two isomorphism problems. Ages ago with Zeke Zalcstein—and independent from Bob Tarjan—I made the trivial but useful observation that group isomorphism can be solved in time 
Later I worked on graph isomorphism using what I call the “beacon set method.” This yielded strong results about random graphs, and also results about special families of graphs. The result on random graphs, for example, allowed an adversary to modify 
The paper was never published—a mistake that one should avoid; publish all of your results. The paper did prove that isomorphism could be done in 
I—Ken writing some of these snippets from papers too—have remained relatively free of the isomorphism bug, except for formulating an open question about classifying “which ‘graph-unravelings’ are
Isomorphism is probably one of the most fundamental problems for any discrete structure.
So we consider the SODA 2014 topics in turn.
Isomorphism For Lattices
The objects are lattices. Wait that word is used a lot in math. It could stand for according to this:
- Lattice (order), a partially ordered set with unique least upper bounds and greatest lower bounds.
- Lattice (group), a repeating arrangement of points.
- Lattice (discrete subgroup), a discrete subgroup of a topological group with finite co-volume.
- Lattice (module), a module over a ring embedded in a vector space over a field.
- Lattice graph, a graph that can be drawn within a repeating arrangement of points.
- Lattice multiplication, a multiplication algorithm suitable for hand calculation.
- Lattice model (finance), a method for evaluating stock options that divides time into discrete intervals.
The meaning used here is: a discrete subgroup which spans a real vector space. Every lattice, in this sense, has a basis and is formed by all integer linear combinations.
Haviv and Regev study the natural question: when are two lattices isomorphic? Here this means that there is a rotation that moves one to the other. This sounds pretty simple, perhaps easy, but low-dimensional intuition often does not work in high dimensions. They prove:
Theorem 1 Isomorphism of lattices can be determined in time
.
They actually prove much more: they find all the possible isomorphic mappings. A very neat result.
Their algorithm “violates” a informal rule that I, Dick, have found to be quite useful. The rule is:
There are no natural decision algorithms whose running time is polynomial in
.
Of course an algorithm that list all the even permutations on 
Isomorphism For Order Types
The objects are sets of 
is positive, negative, or zero respectively.
Not surprisingly this all generalizes to any dimension. Two sets of
The main result of Aloupis, Iacono, Langerman, Özkan, and Wuhrer is:
Theorem 2 There is an algorithm that determines the order type of
points in
-dimensional Euclidean space in time
.
One notable feature of this result is that the points need not be in general position—there is no restriction on they arrangement. This seems like an important feature and should make the result have many more potential applications. An obvious question that occurs to us is: If there is an algorithm for testing isomorphism of order types for general position in time 
We note also that this yields an answer to the question:
How do five people get together to work on one problem?
They started their work together at the 2011 Mid-Winter Workshop on Computational Geometry. So that is how we get papers with many authors. A great argument for more such workshops and meetings.
Isomorphism For Noisy Cases
We can also consider various approximative notions for graph isomorphism. One aspect of this comes from an old paper I wrote in 1999 with Anna Gál, Shai Halevi, and Erez Petrank, titled “Computing From Partial Solutions.” We showed that computing a partial isomorphism—that is getting just 
The SODA 2014 paper by O’Donnell, Wright, Wu, and Zhou is emceed by Konstantin Makarychev in this CMU video, Zhou presenting. That doesn’t quite make five people. Well the paper leans on a hypothesis by Uriel Feige that any polynomial-time randomized algorithm giving one-sided error on random 
Given two graphs 
Given two graphs that are
-almost isomorphic, compute a
that preserves a
portion of edges.
They show that assuming Feige’s hypothesis, there really is no polynomial-time algorithm for this problem. Or put another way, finding a polynomial-time algorithm for this problem suffices to falsify Feige’s hypothesis. This is surprising insofar as GI is not 
Open Problems
Are there more good cases of isomorphism to study? Are there even more relationships to Unique Games? Will SODA 2015 have more than three papers on this topic?
Another problem that is not known to have an O(c^n) time algorithm is Subgraph Isormophism. According to Fomin at al. (JCSS 78(3): 698-706 (2012)), this is not even known for the special case where the pattern graph has maximum degree 3.
Is it possible that an NP complete problem can be reduced to code isomorphism? (Remember the best known algorithm for code isomophism runs in (2+O(1))^n as per Grochow’s result) and there is no reduction from code to graph isomorphism but there is a reduction vice versa.
J: The result you are referring to (if I understand your intention correctly) is Laci Babai’s and not mine; see Corollary 7.1 in the unique paper with coauthors Babai-Codenotti-Grochow-Qiao: https://www.siam.org/proceedings/soda/2011/SODA11_106_babail.pdf.
Proposition 7.2 in that same paper shows that linear code isomorphism reduces permutational isomorphism of permutation groups, which in coAM (Prop. 7.4, ibid) and hence not NP-complete unless the polynomial hierarchy collapses to its second level.
Thankyou. I am correcting my statement to “..as per Babai et al.’s result”.
BTW If you have a promise problem where your input k dim codes in dim space, degree d graphs over n vertices come from a subset of such codes or graphs with the constraint that say the codes have min distance either d1,d2….dS or graphs have max clique size c1,c2,….cS, then is the problem still GI complete?
Say S=2 that is you have d1 or d2/c1 or c2.
The matrix permament is a paradigmatic and eminently practical example of Dick’s principle: the classical permanental algorithm is O(n!); Glynn’s formula is O(n^2 2^n).
Re: “Are there more good cases of isomorphism to study?”
Just off the top of my head, as Data says, there are a couple of examples that come to mind.
Sign Relations. In computational settings, a sign relation
is a triadic relation of the form 
where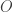 
is a set of formal objects under consideration and 
and 
are two formal languages used to denote those objects. It is common practice to cut one’s teeth on the special case 
before moving on to more solid diets.
Cactus Graphs. In particular, a variant of cactus graphs known (by me, anyway) as painted and rooted cacti (PARCs) affords us with a very efficient graphical syntax for propositional calculus.
I’ll post a few links in the next couple of comments.
Minimal Negation Operators and Painted Cacti
Let
The mathematical objects of penultimate interest are the boolean functions
for 
A minimal negation operator
for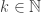 
is a boolean function 
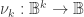defined as follows:
•
•
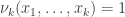if and only if exactly one of the arguments 
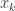equals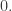 
The first few of these operators are already enough to generate all boolean functions
via functional composition but the rest of the family is worth keeping around for many practical purposes.
In most contexts
may be written for 
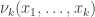since the number of arguments determines the rank of the operator. In some contexts even the letter 
may be omitted, writing just the argument list 
in which case it helps to use a distinctive typeface for the list delimiters, as 
A logical conjunction of
arguments can be expressed in terms of minimal negation operators as 
and this is conveniently abbreviated as a concatenation of arguments 
See the following article for more information:
☞ Minimal Negation Operators
To be continued …
GI: suppose we have adjacency matrices G1 and G2. Graphs are isomorphic if for some permutation matrix P. G1= P^T G2 P. We encode permutation matrix as a set of quadratic equations:
. we have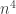 
monomials but 
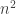equations. But for any numeric matrices A and B the following is true A G1 B= A P^T G2 P B. Therefore, choosing pairs of random matrices we can create enough quadratic equations to derive formally overcomplete system of equations in terms of monomials, and the rest is the question whether there is some strange/interesting reason why we would not be able derive a full rank (in terms of monomials) representation of the right part of initial equation.
Just a crackpot opinion.
Dear Dick, since you’ve spent some time with graph isomorphism problem you may care to comment, giving the reference the following 2 questions. If we have two simple connected regular graphs (we actually do not need regular ones) the isomorphism problem can be stated as L1 P – P L2= 0 (1) where L1,L2 are Laplace matrices of the graphs, and P is a permutation matrix. for connected graph L1, and L2 have only one zero eigenvalue, and the rest are positive, therefore rank L1= rank L2= n-1. (1) can be written as L1 P I – I P L2= 0 and therefore
, where 
is vectorisation of matrix P, stacking its columns. the rank of each term in the bracket is n(n-1), and the structure is quite different. Question 1. what is known about rank and null space of (1) besides trivial one arising from singularity of Laplace matrix.
Suppose the rank of the whole bracket is
then every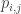 
can be expressed in terms of m last variables by Gaussian elimination. In order to check for consistency one can scan through all possible values of P substituting m-last variables. Adding the quadratic condition on the entries of p one can look at Nulstellensatz certificate and its degree of unsatisfability of the system of equations. My simple experiments (even with L1=L2) show there are too many linear constraints for the certificate to grow fast. Glancing at the literature I did not find this approach analysed. Question 2. What is known about degree of Nulstellensatz certificate in the naive approach to the GI problem. I hope providing references, if they exits, would be good enough for the general audience, as it seems this approach is so natural that somebody have certainly been looking at it, and if not, due to the simple structure may lead to some interesting consequences, that does not require very high end math to analyse. I’m still childish naive to push polymath projects on the high profile smart people blogs.
Strongly regular graph have at most 3 different eigenvalues. The eigenvalues of Kronecker product is all pairwise sums of eigenvalues, which in our case would be all pairwise differences between 3 different eigenvalues, that lead, in worst case, to 4n-6 independent linear equations in n^2 variables. Now the question what can be used in the best algorithm for the strongly regular graphs to increase the number of constraints, which in turn could be used to decrease direct application. (seems like duality in play if that can work).
@maktkov Spectral approach, as a body of knowledge in its current form, is useless against many tough problems in graph theory including isomorphism, Shannon capacity etc. If as Lipton conjectures, the problem is in P, then probably a new representation is needed.
The point is not in the spectrum itself, but in using the eigenvectors too, since two together contain sufficient information about Adjacency matrices. What I’m trying to bring here, without success for now, is the Nullstellensatz linear algebra (see de Loera paper), as a polynomial shortcut to computing Groebner basis. The spectral analysis provides crude approximation of the number of parameters vs. the number of equations. What is also possible, since Nullstellensatz provides a set of constrains, to look for the solution for the isomorphism within the constraints provided by the set of polynomial equations to derive new constraint, and repeat this recurrently, which reminds me duality of semidefinite programs. But that is a fantasy. By the way automorphism is organically embedded in this approach. Anyway, thanks for reply.
Still will not help. Another way to look at the problem is needed.
Let’s put it this way. I believe you and Dick in the hardness of the problem (many smart people thought about it for 40 years and did not find a solution). I believe your intuition about Nullstellensatz (and quite believe of Dick). This intuition should be based on something. Do you mind (any of you) to put references your believe is based on, if not nailing it down. In order to find a new approach a bottle-neck should be identified. What I find hard in math is that very simple approach is buried into so many details, that it easy to be lost even in notation. What we need is simplification to the clear core bottle-neck. Some people say that, research in physics in early XX century would not be possible to publish in today journals due to the lack of rigorous statistical analysis, still at that time it was one of the largest advance in physics.
I think the main difference between polymath and open source, is that polymath was upfront set to the math for mathematicians, whereas open source is open for everyone. In open source there are many tutorials, and even paper references, so anyone interested has so much opportunity for self-education. Let say, hard mathematical problems are attractive, not only by the fame associated with them, but by the simplicity of formulation, and the richeness behind it. It is very good source for self-education too, even if people have very limited time to study it. But I think many people need a guidelines. Therefore, references, at different levels of difficulty, and intuition if it is available!!!
” In order to find a new approach a bottle-neck should be identified.” That says it all. In order to fix an issue, you need to root cause. The root cause is as hard as the proof (whatever that means).
I do not believe poly-math can solve long open problems which require new idea. Usually it requires long periods of focus, trial error, different insights following one after another and so on. If polymath can solve open problems such and such ways of collaboration, it may very well be P=NP. Polymath to me is like a parallel proof attack by different individuals.
In a sense you are contradicting yourself. If
the best way to solve is to guess and check. That is polymath (openmath). You say the opposite – sit quite, and gradually improve with local insights – pretty much the way semidefinite program is solved today. Than either P=NP (the way current research is working, that is an underlying unspoken assumption), or by funding policy we are looking (forced) to select those only problems that can be solved by polynomial algorithms.
What I meant is the guessing cannot be parallelized. If it can be then it may as well be the case the search process itself is efficient.
Ok forget my comments. They are not relevant.
coming back to the idea PA=BP. The problem here is too much symmetry. The following idea is also too simple, but again if someone drop a relevant reference I would appreciate. We augment matrices on both sides with matrices C D E:![\left[ \begin{array}{cc} 1& 0 \\ 0& P \end{array} \right] \left[ \begin{array}{cc} E & C \\ D& A \end{array} \right] = \left[ \begin{array}{cc} E & C \\ D& B \end{array} \right] \left[ \begin{array}{cc} 1& 0 \\ 0& P \end{array} \right]](https://s0.wp.com/latex.php?latex=%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+1%26+0+%5C%5C+0%26+P+%5Cend%7Barray%7D+%5Cright%5D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+E+%26+C+%5C%5C+D%26+A+%5Cend%7Barray%7D+%5Cright%5D+%3D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+E+%26+C+%5C%5C+D%26+B+%5Cend%7Barray%7D+%5Cright%5D+%5Cleft%5B+%5Cbegin%7Barray%7D%7Bcc%7D+1%26+0+%5C%5C+0%26+P+%5Cend%7Barray%7D+%5Cright%5D&bg=ffffff&fg=333333&s=0&c=20201002)
. Now we have much more equations, and the question whether we can choose C and D to limit Groebner basis search to second degree, or an finite degree, and what is the size of matrices C and D are needed. the lower bound is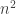 
, since in strongly regular graphs there are only 3 eigenvalues. The best algorithm would use the structure of the null-space in the Kronecker formulation above. Now that would work, because there are papers showing that adding vertices make the isomorphism problem simpler in the spectral sense. The question s only how large is increased problem – any references are appreciated.
and here how we find C D and E. suppose matrix A is
. Take each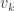 
with multiplicity greater then 1, split it into 2 vectors and augment (concatenate) it with additional vector 
. Now write ![A'= \sum \frac{\lambda_k+\epsilon_k}{2} [u_k; v_k] [u_k; v_k]^T+ frac{\lambda_k-\epsilon_k}{2} [-u_k; v_k] [-u_k; v_k]^T](https://s0.wp.com/latex.php?latex=A%27%3D+%5Csum+%5Cfrac%7B%5Clambda_k%2B%5Cepsilon_k%7D%7B2%7D+%5Bu_k%3B+v_k%5D+%5Bu_k%3B+v_k%5D%5ET%2B+frac%7B%5Clambda_k-%5Cepsilon_k%7D%7B2%7D+%5B-u_k%3B+v_k%5D+%5B-u_k%3B+v_k%5D%5ET&bg=ffffff&fg=333333&s=0&c=20201002)
, where 
, and C is the smallest difference between distinct eigenvalues of A. Then we compute matrices C D and E based on new decomposition and apply them to second matrix. We have 2 large matrices with distinct eigenvalues, and we need to find whether there is a permutation of egenvector values in the original part that lead to the same eigenvectors. Then we apply Algorithm1 from http://www.worldscientific.com/doi/pdf/10.1142/S0129054109006693