In Praise Of P=NP Proofs
Why they can be important
|
|
Advertising source |
Joe Bloggs is not a computer scientist, at least not one that we know. As noted by Wikipedia, Joe Bloggs is a “placeholder name” like “John Doe” or “Jane Roe” in the US, or “Ashok Kumar” in India. Sometimes real people have or acquire the placeholder names: Ashok Kumar (born Kumudlal Ganguly) was a famous actor in India, whose acting brothers also took the surname “Kumar,” and the “Roe” in Roe v. Wade is Norma McCorvey. We especially like the fact that “Joe Bloggs” came about long before there were blogs. A public restraining order is indeed called an “Ashok Kumar order” in India the way it is called a “John Doe order” in the US.
Today Ken and I consider whether there should be a “John Doe order” against submitting claimed proofs of 
I know this is at variance with the general attitude that such proofs must be wrong, and looking at them is a complete waste of time. I would like to explain why this is not the case. Ken and I have spent a good deal of time looking at such proofs—they do come in at the yearly rate suggested by Gerhard Woeginger’s P-versus-NP page While there are attempts and there are attempts, we think that subject to minimal criteria, it is fruitful to look at them.
Let’s explain why.
Reason I
The proof could be correct. We have discussed many times before that in mathematics people often had valid proofs that were at first rejected. Often they were only later found to be correct after another more mainstream proof was discovered. One of my favorite examples is the proof by Kurt Heegner of the beautiful theorem:
Theorem 1 Let
be an imaginary quadratic field whose ring of integers has class number one. Then
where
is one of
Recall class number one means that the integers have unique factorization.
Heegner was a radio engineer and published his “proof”” in 1952. Few believed it. In 1969 the the eminent number theorist Harold Stark solved the problem. To his great credit he went back and re-read Heegner’s proof and realized it was essentially the same as his. It had some minor errors that were easily fixed. See this exposition by Jeremy Booher for more details.
This speaks however the first minimal requirement: The proof should have a short “elevator pitch” as to why it can be correct, quite apart from saying to read the details. What is the new idea that others have not seen or appreciated, and how is it used in the proof? How can it surmount known barriers to the conclusion? This needs to be stated up-front.
Reason II
The proof could be wrong, but 
This speaks to the issue of distinguishing “true efficiency” from “galactic algorithms” which while technically polynomial have running times like 
Reason III
The proof could be wrong, but interesting. The most important reason I believe is that failed proofs have in a number of cases helped create new mathematics. The best example of this is probably the work on extended formulation of polytopes. This notion was created by Mihalis Yannakakis in an attempt to show that a whole class of proof structures for
Yannakakis was motivated by the attempted proofs by Ted Swart that 
I am sure that Swart was greatly disappointed that he did not solve
Yannakakis’s work has in this decade been actively pursued by Sebastian Pokutta and his colleagues. They began by removing the “symmetric” condition on the kind of formulations ruled out, and then liberalized the kinds of extensions. Their work has greatly extended the range of “no-go” theorems, but quite apart from this negative purpose, has created a lot of beautiful mathematics. Moreover their work links several areas: it began with some new thoughts in quantum communication complexity, and has greatly increased our understanding of the structure of polytopes. Ken and I have still been struggling with its exact reach.
Thus our third minimal requirement is that the proof should engage neighboring areas of theory. As we have said before, this should include deriving some lesser consequences, short of shooting the moon. If you’ve proved “equal,” is it easier to see why factoring has a sub-exponential time algorithm? If “not equal,” can you say why 
Open Problems
What do you think? Is there a possible proof out there that we will avoid reading that is correct, or useful, or contains some interesting new ideas?
[fixed “ideals”–>”integers” have unique factorization]
It is unclear why you only discuss P=NP “proofs”. For these there is typically an easy litmus test: If the claimed algorithms obviously would have small polynomial running time if correct, then there are SAT solver competitions that the authors should be able to enter and win if they are right. In a sense this reduces the question to a computer check of the details. (I understand that Swart’s attempt at a proof was not of this form, but many of the claims I have seen over the years have been of this form.)
The solution above is much easier than with P!=NP “proofs” where it is hard to avoid dealing with delusional authors. When a new purported proof first has shown up I have occasionally patiently responded to authors about why they were making unjustified assumptions and how they have missed some key things. About 3/4 of the time, the authors’ have retained delusions, often for many years…
In my experience, the problem is in the gap of the the language you explain and the language they understand, even if they are willing to understand. Which comes to the time you willing to spend to explain, and the time they willing to spend to understand. This is covered by the public opinion not to explain, since “it is junk” by common believe, therefore, the students that have more time are also rejecting to explain, or failing to find good enough arguments. That all comes to huge gap in the language (say in operated abstractions), and we do not have a good resource to step-by-step approach to understanding. For example, it took couple of years to embarrass people to get very simple counterexample, seem to be known for long time. #64 in the list. PS It is hard to talk to mathematicians, they seem to accept only explicit feasible path algorithm in SDP terms, whereas there are exists infeasible path algorithms (e.g. a set of wrong steps), which also can solve the problem.
Paul, in one case the algorithm is near the edge of testability on nontrivial cases, in another it’s “n^{10,000}.”
This is another interesting post on P vs NP. I have noted that in the Gerhard Woeginger’s P-versus-NP page no one yet claimed proof through the algorithmic proof of planar graph three coloring problem which known is a polynomial complete. I am afraid I would be first (victim) along this line and hope at least fall in the line of works by the Reason III if it is verified to be wrong.
At this time see my (draft) presentation prepared for ICM 2014 SEOUL.
https://www.academia.edu/6807631/The_Big_Bang_Theory_of_Planar_Graph_Coloring_Solution_of_the_Three_Color_Problem
Link correction
https://www.academia.edu/6808424/The_Big_Bang_Theory_of_Planar_Graph_Coloring_Solution_of_the_Three_Color_Problem_
What is this “The Big Bang Theory of Planar Graph Coloring”?
Simple. The mathematical rule (like a physical law) must be unique and unified within the whole of the universe created by “the Big Bang of Planar Graph Coloring”. That is it is only the event of the “crash” that makes the chromatic number 3 or 4 for each of planar graph classes. And by the spiral chain coloring algorithm (SCC) not only color vertices of the graph exactly with number of colors not more than the chromatic number but detects “a crash” efficiently (forcing the use of fourth color) and eventually. That is clearly imply that P=NP..
“Recall class number one means that the ideals have unique factorization.”
This is wrong. Ideals in a number field always have unique factorization. Class number one means that all ideals are principal, which is equivalent to unique factorization of numbers in the ring into irreducibles.
Thanks—fixed.
To my way of thinking, boolean universes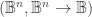
are some of the most fascinating and useful spaces around, so anything that encourages their exploration is a good thing.
I doubt if there is any such thing as a perfect calculus or syntactic system for articulating their structure but some are decidedly better than others and any improvement we find makes a positive difference in the order of practical problems we can solve in the time we have at hand.
In that perspective, it seems to me that too fixed a focus on P versus NP leads to a condition of tunnel vision that obstructs the broader exploration of those spaces and the families of calculi for working with them.
Maybe physicists are right and P=NP, but only during inflation.
http://qbnets.wordpress.com/2014/03/30/the-inflationary-quantum-computer/
hey great pov, thanks for having the cojones to express something so controversial & support you wholeheartedly on this (partly from long reading your blog), have been thinking of cooking up some similar case for the defense & swart is a great example/case study; but alas its a strong minority view, know this from long experience on subj. 🙁 the numerous proof attempts take a lot of time to sort thru, have done some of this myself over the years but it can be a really thankless and difficult job.
have long thought at times it would be nice to attempt to create some kind of community involvement/organization for these attempters/attackers, but so far they all are rather highly disconnected, and the existing community basically shuns them as taboo, and occasionally outright mocks them. one might think there is some strength in numbers but so far there is only quite the opposite. talked once to a elite TCS authority “AR” and he basically laughed outright at the idea any would have any redeeming value to be considered by anyone.
this attitude can be seen on one of the premiere online TCS societies (of which youre a member), tcs.se, in the meta section here and here…. etc! if you feel really daring try posting this exact same pov in meta & see what happens! think youll find its a very tough sell tested against real online scientific opinion no matter how high your own “rep”! not only is it a tough sell but there is already very strong pushback even in somewhat “looser” online communities….
Support for this policy comes from Grothendieck’s maxim
It might be helpful to commit to a short list of simple questions about a proposed proof to an open problem. We could use it as a gateway (or rather, a filter) for potential proofs. If an author can give competent answers to the questions, then the proof should reasonably qualify for review. It might also help people know a little bit about what researchers expect.
Which questions would you ask?
Suppose I have a claimed proof that P!=NP (or P=NP). Give me a small list of questions that should be easily answered if I have competently composed a proof.
There are some checklists that people have created (e.g. Scott’s: http://www.scottaaronson.com/blog/?p=458), but they are directed at identifying bad proofs rather than identifying potentially okay proofs. Also, some can require a lot of background that a non-complexity theorist might not have. If I am an outsider to TCS, then it generally might be too much to ask that they immediately check their approach with obscure lower bounds on special types of circuits.
Is this protocol unreasonable or too difficult to design?
What are the most useful one or two things that you’ve personally gleaned from reading an incorrect proof of P=NP (or its converse)? Anything?
The quantum indetermination of time vs. energy at microscopic scale is likely to get dramatically amplified through algorithmic iteration, giving rise to some quantum indetermination of time vs. information of the data at macroscopic scale. In view of that, you may interpret the information carried by the input and output data – or the information provided by a solution check – as a genuine quantum magnitude.
The distinct degrees of computational complexity – experimentally witnessed inside the NP class – might thus be the macroscopic expression of mere quantum levels of energy within the computing material. The hypothesis that P!=NP then becomes a convenient but unprovable rephrasing of a quantum phenomenon.
Is that possible, or completely silly?
Let me express myself a little more clearly.
The time -energy indeterminacy at Planck scale on the encoded data in a computer process gets amplified through algorithmic iteration, which produces a computable time-information indeterminacy on the macroscopic data. The information contained in the input and output data of an algorithm may be viewed as a quantum magnitude, subject to the uncertainty relation ΔI . Δt ≥ ℏ where Δt is the minimum time that’s physically required to compute a data of information I with accuracy ΔI.
A problem in NP is called hard whenever its time-information indeterminacy grows faster that the size of its input data, making its resolution probability close to zero. The discrete degrees of computational complexity inside the NP class are the macroscopic image of energy levels within the physical processor. The statement P≠NP is a mathematical translation of this physics phenomenon. The experimental leaps between polynomial time, sub-exponential time and exponential time inside the NP class are nothing but quantum leaps.
Therefore, all proofs of P≠NP or P=NP are doomed, since those assertions are devoid of physical content. Yet, they still make sense mathematically. P≠NP means that everything which exists is computable. P=NP means that there are some objects which, despite being uncomputable, still have an ideal mathematical existence. It looks like the assertion that there are non-standard elements in the set of the natural numbers. A world where P=NP can be viewed as a sort of Alexandroff extension of a world where P≠NP.
Long time ago in 1974 when I was with THE (Technical University of Eindhoven) I heard similar argument from a visiting scholar John Savage (Brown Univ) that space-time tradeoffs of computational complexity has an analogy with the Heisenberg uncertainty.principle. I am sure someone can give an detailed account on this direction.
If that account was detailed enough, “someone” might get the Millennium Prize with it… 🙂
there seems to be some “master time/space tradeoff” theorem waiting to be uncovered in complexity theory. to me it is highly related to data compression. its a big elephant in the room. but right now its mostly just the blind men and the elephant. sometimes a single theorem can lead to a thousand existing theorems as corollaries. it has long felt to me like a big gem like that, a sort of unification theorem, is waiting to be uncovered in complexity theory & it probably lies very close to a P=?NP proof.
I don’t think a theorem of math will ever teach us why it takes more time to uncompress a data when its compression rate increases. Otherwise that should have already been found long ago. Perhaps what’s missing is rather some kind of informational relativity principle, something like “you can’t compute a data with more accuracy than you can know the energy of its phisical components”…
Currently, the point (P = ? NP) should be demonstrated that existence of one-way functions implies existence of one-way permutations. If entropy is a one-way function, can we find systems allowing a one-way permutation with a physically-motivated symmetry group (i.e., with entropic boundary condition)?
entropic boundary condition (one-way function) = second law of thermodynamics = uncertainty principle.
We have two or three cases where someone from outside made major contributions, a few more cases where what they said unintentionally inspired interesting development, and we have thousands of cases where nothing good came out of them. It is fine that you encourage reading hobbyist proofs. It is not so if you encourage them to contact us, that is what your post is doing. It is not that they send their proof just to you and Ken, they send them to all of us. Unlike you many of us don’t want to receive these emails. I have started getting phone calls from these random guys asking me to look at their P=NP proof or help them write one for their algorithm. It is extremely unpleasant. True, we might learn something interesting from them, but we might learn something interesting from anyone, there is nothing special about these people other than being rather unpleasant to deal with: lazy, demanding, arrogant, ignorant, rude, suffering from grandiose delusions and messiah/god complexes, … They took over comp.theory and made it unusable for us, We use ECCC in place of arXiv’s cs.cc because of them. Don’t you think we have had more than enough of them? Outreach means attracting folks who want to learn and listen, not ignorant hobbyists who want to lecture us about their disillusions.
“lazy, demanding, arrogant, ignorant, rude, suffering from grandiose delusions and messiah/god complexes, … ”
Sounds like you
That is where we need one place to look over the illusions, explained by the community to high school kids, what is wrong and what is right. The real crowd thinking. It will have a great educational value and relieve the necessity to contact top theoreticians. Open online university to learn in self pace speed, asking stupid questions and finding the way to improve. I understand what you say. I’m saying we have very big gap between people on the ground and on the Everest, and there are no Sherpas to guide. I’m felling this is one of the major reason we stuck in current social model.
Dear Drs. Lipton and Regan,
Thank you for helping to shed light on new ideas about TCS, like some of mine:
1. Language Incompleteness
2. NP-Completeness Incompleteness
3. SAT’s weakness
4. generalization of TCS concepts (The Barbosa’s Program)
5. Observer-Dependency Complexity
6. Cook-Levin-Barbosa Theorem
7. NP/NPg-Completeness
8. Barbosa Panfinite and Hyperfinite Fraction Numbers
… and counting, at
1. http://arxiv.org/ftp/arxiv/papers/0907/0907.3965.pdf
2. http://www.andrebarbosa.eti.br/The_Cook-Levin_Theorem_is_False.pdf
3. http://www.andrebarbosa.eti.br/The_Size_of_the_Hilbert_Hotel_Computer.pdf
You should prune your papers of the insults to others and the self-aggrandizing bits. I don’t know why you think that is okay.
Dear mdxn,
If possible, quote those “insults to others and the self-aggrandizing bits”, please.
I am willing to give you feedback on the attitude in the papers. However, I need you to to commit yourself to how you are going to take and use the feedback first. What I don’t want is a situation where I show you these issues, then you argue them back. If you end up debating or rejecting everything I say, then I don’t see how a dialogue is going to be productive.
Something similar would be beneficial for discussing your works, too. When you go into a discussion about the correctness or merit of your claims, you should think of the following:
Under the presumption that you are wrong or mistaken, are there reasonable and acceptable means for others to demonstrate this to you? If you are unwilling to do and specify this, then it is no better than just assuming you are right.
Dear mdxn,
If I don’t know what you complain about my papers, then I cannot answer it neither compromise myself with it.
another remarkable aspect of P=?NP proofs is how many are written by apparently very highly trained authors, many have Phds. so what exactly does this say about the Phd system? o_O
its a question few Phds are willing to face/discuss.
ps weird coincidence, there was a recent P=?NP attempt on arxiv, which of course is not uncommon, but just saw this rebuttal by academic researchers which is highly uncommon.
also want to say there is a common misperception that woegingers list is a list of refuted proofs. it is nothing of the kind. it can strictly only be taken as a list of unverified claims
In my experience, people who put PhD after their name are usually selling dodgy nutritional supplements or something similar. This is not a criticism of the PhD system, rather the reverse – it is thought to add a veneer of respectability …
not exactly sure what your point is. that many who have Phds do not openly state it? the writers of this blog have Phds & its open knowledge. while some claims of earned Phd degrees by P=?NP attempters are false (is that what you are insinuating?), presumably most are accurate. many on the woeginger list have Phds or advanced degrees eg masters etc.
Here is my point in Noam Chomsky’s words:
“In mathematics, in physics, people are concerned with what you say, not with your certification. But in order to speak about social reality, you must have the proper credentials, particularly if you depart from the accepted framework of thinking. Generally speaking, it seems fair to say that the richer the intellectual substance of a field, the less there is a concern for credentials, and the greater is the concern for content.”
dont really know what chomsky’s point there is, think its verging on outright wrong, & feel like youre missing one (but congratulations on finding a vague contextless quote that seems to support your position (whatever it is). he has a Phd… scientific fields & research have run off academic credentials for centuries. they are tightly coupled… he might be talking about an expert from one field being allowed some leeway in another…
I don’t believe this is a respectability or vanity issue. I’m under the impression that, in the medicinal field, its important to put PhD or MD after your name to distinguish yourself from the other. You need an MD to legally write prescriptions. A PhD (researcher) in medicine alone does not let you do this. I think somewhat similar reasons apply for specifying J.D. from a PhD in law.
Obviously, in other fields such as math and CS, these subtle differences don’t exist.
That rebuttal is by undergrad students, not career academics.
thx for the clarification! they mentioned affiliation with rochester CS dept but did not mention their undergraduate status in the paper. an unusual undergraduate exercise! admittedly the following assertion will like be just as controversial as the position espoused in this blog, but to me, somewhat worthwhile. wish that there were online P vs NP study groups or chat rooms…. have chatted on it on stackexchange over few yrs but the chat rooms there tend to be mostly infrequented…. RJL if you are ever in a wild mood try having some office hours in an online chat room…..! 😀
rats sorry messed up the link. take2 here is the rebuttal
Congratulations for this post in praise of new ideas on TCS.
Let me praise the “praise of P = NP proofs” by carrying on the spirit carried within: short elevator pitch.
The proof this time is, unfortunately not on P, NP, or coNP, but on one almost totally unrelated: The Riemann Hypothesis.
How does one go about proving RH? Staring at roots (1/2 ± δ) ± it?
In a sense, YES. That is exactly one way to do it. Any doubt?
RH in essence is: δ = 0. No doubt about that. Equivalently: (1/2 ± δ) ± it = 1/2 ± it (!)
We can of course restrict our attention to the upper half of the complex plane, or in math jargon: WLOG, since the lower half can be dealt with the same way.
In other words: RH is true, if (actually iff) (1/2 ± δ) + it = 1/2 + it. Obvious? No?
The above is nothing but (1/2 + δ) + it = 1/2 + it = (1/2 – δ) + it, implying (1/2 + δ) + it = (1/2 – δ) + it, or better δ = -δ. Staring at it, are we there yet?
If not, let us assume that in Heaven we gain the extra mental power of God and see things clearly (or if you prefer, God and you become one up there). Let us say that there is a way that rolls us (together with cj = (1/2 + δ) + it and ck = (1/2 – δ) + it) up into Heaven. Let us call it RollUpToHeaven. In math gibberish, it is likely something called mapping and, instead of RollUpToHeaven(c), we have something, more Heavenly, like f(c). So far, so good?
Therefore, (in Heaven) f(cj) = f(ck). Bravo! We see! But wait… Coming down to earth, we again lose that extra mental power (and our worldly memory is incapable of having the nice time in Heaven persisted). Even if we go around showing folks f(cj) = f(ck), we get that blank stare. Earthlings have no connection to God’s stuff. It is like the Heavenly f(ck) looks not much different from f(ck) or f.ck., and has hardly any meaning beyond. We seem firmly earthbound with our Heavenly visit null and void. Any hope?
Ah! You got it. Yes, only if we can let f preserve things back down to the earth! In math, we say “if the relation is preserved”. Concretely, RH is proved if the Heavenly equality of f(cj) = f(ck) is preserved (down to the earth to give us cj = ck). The technical details are boring. If interested however, please visit:
http://www.cqr.info:2013/MolyGrails/riemann-proof
Thanks for your interest!
Note: Thought that tags and symbol codes will work. But obviously not in every case.
cj, ck: are actually c[j] and c[k], j and k are subscripts
±: +-, plus sign over minus sign
May be others that I have not spotted.
Sorry for the mess.
this is enough for me. i cant read anymore.
The above is actually a spam comment for cosmetics, but it was singularly appropriate so it got modded in. It may become a spam-experiment…
Pip,
I hope your message is not labeling my post as ‘spam’.
It is not. It IS a serious attempt.
Basically in more or less math terms it is the following:
It claims that Zeta is an isomorphism mapping from (C, +) to its range. (C, +) is obviously a group.
Let a = ½ + d + it and b = ½ – d + it. Since isomorphism (of groups) preserves relationships, including EQUALITY, therefore Zeta(a) = Zeta(b) = 0 implies a = b.
The two are of course any ‘complementary’ zeros of Zeta, namely, ½ + d + it and ½ – d + it (or the conjugate ½ + d – it and ½ – d – it). I do not think anybody could have problems with that.
Since (if) Zeta is an isomorphism, Zeta(a) = Zeta(b) (= 0) implies a = b, which in turn implies, obviously, d = -d (that is d is zero!). And that is the solution to RH.
You see any problems?
I cannot easily write the entire thing in the post not running the risk of having the mess such as ±. There is, I believe, no way of editing once I post.
I apologize if I gave people a hard time. It was not intentional.
To be open-minded is commendable. Let people speak and try to understand what they are trying to say.
With all that being said, if you or anybody have/has questions, please ask. Other ways of expressing oneself may not be that effective.
Regards,
TCNE
P.S.
The proof link may not work perfectly for all browsers. It was tested for FireFox, IE (7+ I believe), and Chrome. If anybody has difficulty, please let me know. Thanks again.
Lol Pip.
TCNE, unless you == “jessica moreh” it was not a reference to you :-).
Ken,
Thanks so much for the clarification.
I truly can not know for sure what jessica was really talking about. It could be the messy post I had. I again apologize.
I just wanted to be sure.
Thanks again
Regards,
TCNE
Bugger, someone got in before me! Anyways, here goes…
“Hi, my name is Phill and I’m a math’s crank.”
There, that feels better already…
Thank’s for a great post and thank you John Sidles for the very apt quote of Grothendieck’s; Craindre l’erreur et craindre la vérité est une seule et même chose.
(Fear of imprecision and fear of illumination are one and the same)
I’m using that.
All the problems and pitfalls of bluster, ignorance and incomprehension inherent in the amateur attempt are lain out in the post and iterated in the subsequent comments. ‘Catch-22’ & ‘so it goes’, to paraphrase Heller & Vonnegut…
That being said, I’m much interested in the discussion points reiterated by Serge, Vznvzn & Alexandre, regarding a purported link between quantum (or quantized?) error and the problem of P Vs. NP, also with the conjecture by Alexandre about mathematical/physical analogues of entropy pertaining to one way functions?
In consideration of those particular questions, alongside all the caveats outlined in the original post, I respectfully invite you to inspect my humble, ‘halting’ attempt, at a mathematical harnessing of error & entropy. Please comment freely…
http://unitambo.wordpress.com/spreadsheet-model/
http://unitambo.wordpress.com/one-way-function-with-trapdoor-table-pre-print/
Thanking you in anticipation.
Hi Phillip, regarding existence of one-way functions implying existence of one-way permutations…here’s a paper:
https://www.researchgate.net/publication/261912303_One-way-ness_in_input-saving_%28Turing%29_machine?ev=prf_pub
Hi Phillip, regard existence of one-way functions implying existence of a particular
one-way permutation (two successive controlled-NOT quantum gates)…here’s a paper:
https://www.researchgate.net/publication/261912303_One-way-ness_in_input-saving_%28Turing%29_machine?ev=prf_pub
Hi Phillip, regarding existence of one-way functions implying existence of a particular
one-way permutation (two successive controlled-NOT quantum gates)…here’s a paper:
https://www.researchgate.net/publication/261912303_One-way-ness_in_input-saving_%28Turing%29_machine?ev=prf_pub
Fascinating stuff Alexandre, I was only vaguely aware of Bennett’s ‘thermodynamic’ Turing machine model…
It’ll take me a little while to digest (his &) your paper(s) fully but on the surface of it, ‘entropic boundary conditions’ would appear to equate with the ‘conditioned equation’ requirement of my paper and also, the matter of encryption being dependent upon entropy constraint/conservation?
I’ll get back to you when I’ve processed this more thoroughly.
Meantime, while my brain is ‘tupling’, thanks very much for the link & views!
I hazard to suggest… I’m describing a numerically ‘quantised’ (deliberate use), two-state system?
Terry Tao’s web indispensable web page “Career Advice“ includes (among its many outstanding advice-links) a link to Richard Hamming’s essay “A Stroke of Genius: Striving for Greatness in All You Do“:
This amounts (as it seems to me) to the advice that Borges gives in his story Averröes’s Search
Of course, elsewhere in this same story Borges writes “Only the man who has already committed a crime and repented of it is incapable of that crime; to be free of an erroneous belief one must at some time have professed it.” Similarly Grothendieck warns us “To be afraid of error and to be afraid of truth is one and the same thing”; Réné Thom admonishes “The boundary of the true is not the false, it is the insignificant”; and Terry Tao’s essays “Ask yourself dumb questions – and answer them!” and “Continually aim just beyond your current range” are meditations upon this same theme.
Conclusion The chorus of Tao, Borges, Hamming, Thom, and Grothendieck reminds us that kooky and/or dumb ideas usefully illuminate for us that “what we seek is often nearby” … even when — especially when! — kooky ideas are expressed with sufficient concision, rigor, and clarity, that we can enjoyably gain even in explaining plainly to ourselves (and colleagues) why they are wrong.
As Groucho Marx said in his inimitable fashion: “Those are my principles, and if you don’t like them… well, I have others.”
I also agree that a solution to P=?NP might lie substantially closer than is commonly believed.
The idea that information could get its indeterminacy from iteration might be dubious after all, but the original insight that complexity is at the bottom line an expression of quantum indeterminacy remains valid to me. Indeed, complexity inside the NP class is a phenomenon that crosses all the metamathematical barriers. So much so that you can never prove that a given problem is complex, since its complexity is likely to get transferred to the complexity of your proof. This is precisely the nub of the PvsNP problem.
Therefore, it’s not excessively kooky to claim that complexity also crosses the physical barrier – and changes its name in the process to “indeterminacy”. After all, computers and colliders are not so different machines. It’s just that computers use a better tamed form of energy which is called information. As crazy as this may sound, programming – and more generally, thinking – is indeed an attempt to reduce quantum indeterminacy.
Note that I might not be the only one who thinks this way. I’m told that some professional mathematicians – including Fields medalist Alain Connes – have been trying to solve the Riemann Hypothesis by quantum arguments…
Or maybe wet get a feeling of hardness because the creative part of our brain is a quantum computer – and this would be where the quantum indeterminacy comes into play. In any case, NP-complete problems are hard because they’re *unlikely* to get solved. Complexity defined as “the fastest algorithm that solves a problem” is an elegant polite fiction that Nature has nothing to care about.
Invalid proofs can still be interesting, but only if they are written well. Here is my invalid proof that P is not NP: http://arxiv.org/pdf/cs/0310060v8.pdf
I think it is worth reading even though it is invalid, as it is an interesting approach.
One shouldn’t feel bad about making mistakes. The object of doing research is to learn, not to always be right.
Phillip, I’ll see what you have done.
Cheers Alexandre!
The S.S model (Excel link) is worth a look to verify numerical procedures.
(& confirm Excel number voodoo not at work…)
At the heart of it, an injective fractal function.
A surjective inverse guaranteed accurate to within +/- 1 u.l.p.
The function able to maintain discrete, scaled, iterative, binary modulated output. (1 bit)
Forward casting of a priori error state with approx 1:3 opportunity for free binary encoding.
Need for binary ‘trapdoor’ index file (further 1 bit) to enable inverse regression.
‘Hard’ (impossible?) to invert without both function ‘hash key’ or trapdoor file.
Thanking you for your attention, let me know if I need to clarify anything?
Regards,
Phill
If nothing else, a novel way of navigating PSPACE with some form of ATM?
(I’d termed it a ‘quasi’ or ‘semi’-deterministic TM…)
In the U.S. “ATM” means “Automated Teller Machine” …
Insert your own joke about P$PACE here …
Does an Alt-TM Dispense Bitcoin$ then?
No one has ever emailed me a proposed proof that resolves P vs NP. But, hey, I’m just a first year graduate student so I’m usually the one whose sending the emails.
I thought about it and I think it would be hard to say no to someone who says the following:
Dear [Blank],
(1) I am passionate about the P vs NP problem for [blank, blank, and blank reasons].
(2) I’ve extensively worked on the problem for [blank many] years.
(3) I’m very particular when it comes to writing up my constructions and I spend weeks/months organizing my ideas to create the clearest, shortest, and simplest presentation.
Please consider collaborating with me. I would like to discuss some of my recent attacks at the problem. Any time you are willing to provide would be greatly appreciated.
Regards,
[Blank]
I would probably respond by asking what their schedule is like and trying to set-up a regular time to chat on the phone. Maybe later on it could escalate to sharing manuscripts.
What do you think??
Dear Michael Wehar,
What is your email address?
You’re guna have to search for it. 🙂
Ok. 🙁
It shouldn’t be too hard to find.
Here is a shameless promotion for my proof, which I know everyone will love: http://www.youtube.com/watch?v=xCzwlrNQQGo
Curious paper about P versus NP problem
http://hal.archives-ouvertes.fr/hal-00984866
Do you think is a serious proof?