A Panel On P vs. NP
A discussion on the famous problem
William Agnew is the chairperson of the Georgia Tech Theoretical Computer Science Club. He is, of course, an undergraduate at Tech with a multitude of interests—all related to computer science.
Today I want to report on a panel that we had the other night on the famous P vs. NP question.
The panel consisted of two local people, one semi-local person, and two remote people—the latter were virtually present thanks to Skype. The local people were Lance Fortnow and myself, and the semi-local one was Dylan McKay. He was present at the panel, and was an undergraduate a bit ago at Tech. He is now a graduate student working with Ryan Williams, who both are moving from Stanford to MIT. The last was the Scott Aaronson who is not only an expert on P vs. NP, but also all things related to quantum computation.
An excellent panel, which I was honored to be part of. We had a large audience of students, who were no doubt there because of the quality of the panelists: although—sandwiches, drinks, and brownies—may have had some effect. They listened and asked some really good questions—some of which we could even answer.
The Panel
The panel, like many panels, was fun to be on; and hopefully was informative to the audience. I believe the one point that all on the panel agreed with is: we do not know very much about the nature of computation, and there remains many many interesting things to learn about algorithms. I like the way Ryan put it:
We are like cave men and women banging rocks together and trying to see what happens.
This is not an exact quote, but you get the point: we are in the dark about what computers can and cannot do.
I thought I would summarize the panel by listing just a few questions that were discussed.
- Are there approaches to lower bounds that are promising?
- What is the relationship of quantum computing and P vs. NP?
- Could P vs. NP be independent of set theory?
- What would P=NP mean if it was true?
- Why are SAT solvers able to solve many “real” problems?
Irony and Self-Defeat
Scott recently released a 121-page survey on P versus NP. He did not read all of it during the panel. In fact he did not read any of it. It is chock full of content—for instance, the story about the Traveling Salesman Problem and Extended Formulations is told in a long footnote. It was partly supported by NSSEFF, which is not a phonetic spelling of NSF but stands for the National Security Science and Engineering Faculty Fellowship, soon to be renamed for Vannevar Bush.
It takes the stand that 
The climax in sections 6.4 and 6.6 is what Scott calls “ironic complexity” and Mulmuley calls the “flip”: the principle that to prove a problem X is harder to compute than we know, one may need to prove that another problem Y is easier to compute than we know. This gets dicey when the problems X and Y flow together. For instance, a natural proof that the discrete logarithm is nonuniformly hard to compute makes it nonuniformly easier to compute. Hence such a proof cannot give any more than a “half-exponential” lower bound (see this for definition). Ryan’s result, which originally gave a “third-exponential” lower bound on 
For my part—Ken writing this section—I’ve experienced a phenomenon that calls to mind our old post on “self-defeating sentences.” To evade the natural-proofs barriers, I’ve tried to base hardness predicates 
The Baur-Strassen 
So maybe the constructive fact behind a problem’s NP-completeness also embodies a mirror image of a problem in P, so that we cannot easily tell them apart. NP-complete problems may “masquerade” as being in P—since the known ones are all isomorphic, if one does they all do. This may explain the success of SAT-solvers and suspicion about P=NP being independent as voiced during the panel. It also suggests that intermediate problems may bear attacking first.
Open Problems
At the conclusion of the panel Agnew, who moderated it skillfully, asked the question:
If you had to state what you believe “at gunpoint” what do you believe about P vs. NP?
He was holding a Nerf gun, but we still all seemed to take the threat seriously. Not surprisingly, all but one “fool” said that they believed that P is not equal to NP. The sole fool, me, said that they felt that P=NP. I have stated this and argued it many times before: see this for more details on why.
Of course P vs. NP remains open, and again as the panel all agreed—including the fool—we need new ideas to resolve it.
[deleted sentence about “not considering P=NP”]
These days, at gun point, I think I have to jump camp and say that I strongly doubt that they are equal.
My uninformed sense of SAT was that it probably partitionable into 3 types of problems. Those that are in P, those that are unsatisfiable and possibly a small number that needs exponential time because they are intrinsically complex. Thus if you default to unsatisfiable after a fixed time, only a small number of answers will be wrong. If almost all real world problems are not intrinsically complex then an approx answer will be quite trustworthy.
Paul.
Maybe proofs should be checked at gun point too. We missed that one in the previous discussion… 🙂 Well, I’m glad no one’s holding a gun at me right now because I really don’t know what to think about PvsNP, and I’ve changed my mind several times on this issue. I feel that everything behaves as if P!=NP, although I can’t tell if that’s because P!=NP or because proving P=NP is to hard.
I’m not even sure mathematics has to be the same on the whole Universe. Information travels at light-speed, and it is understood even more slowly. So two planets that can’t communicate with each other should allowed, in principle, to develop mutuality contradictory theories. And even on out same blue cherished planet, I’d bet that mathematicians who manage to understand a proof of P!=NP are completely unable to understand a proof of P=NP, and the other way around. It’s a question of mental sanity. That’s why we may indeed have both P=NP and P!=NP, with nobody being able to exhibit a contradiction. And all this, without having to travel to the other end of the Universe – which is an impossible thing to do anyway.
And if P is less than or equal to NP ?
If truth is, as I believe, a relative notion then it’s only by accident that a population sees P less than NP, and that another one will see them equal. The good news is that nobody can raise a contradiction out of this situation. The bad news is that opinion-like theorems can never be proved.
Serge,
The probability of solving a NP problem is:
Pr < 1/(positive poly(x)), with x={0,1}. And all positive polynomials over F_2^n reduces x^2+x+1(mod2).
Remember x^2+x+1(mod2) is power set, then, x^2+x+1(mod2) 1/(positive poly(x)), which is the probability of solving a P problem.
Are P and NP are equipollent? (Think of Cantor–Schroder–Bernstein theorem).
I have shown, formally, this here:
https://arxiv.org/abs/1609.01541
(rectifying)
Serge,
The probability of solving a NP problem is:
Pr < 1/(positive poly(x)), with x={0,1}. And all positive polynomials over F_2^n reduces x^2+x+1(mod2).
Remember x^2+x+1(mod2) is power set, then, x^2+x+1(mod2) 1/(positive poly(x)), which is the probability of solving a P problem.
Are P and NP are equipollent? (Think of Cantor–Schroder–Bernstein theorem).
I have shown, formally, this here:
https://arxiv.org/abs/1609.01541
(rectifying2)
Serge,
The probability of solving a NP problem is:
Pr < 1/(positive poly(x)), with x={0,1}. And all positive polynomials over F_2^n reduces x^2+x+1(mod2).
Remember x^2+x+1(mod2) is power set, then, x^2+x+1(mod2) less than x^2+x+1(mod2). Hence,
Pr greater than 1/(positive poly(x)), which is the probability of solving a P problem.
Are P and NP are equipollent? (Think of Cantor–Schroder–Bernstein theorem).
I have shown, formally, this here:
https://arxiv.org/abs/1609.01541
I enjoyed participating in the panel! But:
A short section titled “Why is Proving {\mathsf{P \neq NP}} Difficult?” does not consider the possibility, “because P=NP.”
I’m not sure that’s fair: after all, the very first sentence of the section is, “Let’s suppose P!=NP”! I.e. it’s not that the possibility of P=NP never occurred to me; rather it’s that that possibility (and how seriously we should take it) was already discussed in the section immediately prior, so then it was time for a section about the question of why P!=NP might be difficult to prove assuming that it’s true.
Hi, Scott—you’re right, it
iswas a bit unfair. I did pull your “invisible fence” (“fine line”) observation from that previous section so I wonder why I had that impression. The previous section dwells more on independence, so maybe the segue is better if the first sentence in that next section says, “Let’s suppose P != NP and that it is not independent.” I also felt discussion of Robertson-Seymour theory should go in that previous section. You’ve put it earlier in a footnote on page 9 in section 1 alongside Knuth’s citing it as “pro” P=NP, but the context isn’t so much parameterized complexity as what was called “the loss of innocence of P” in the 1980s. This quip was meant specifically as opposing the Cobham-Edmonds thesis that polynomial-time algorithms once found tend to improve concretely. (Well it is true that the exponent of one of the key R-S routines was improved from 3 to 2, but constants and effectiveness are still hideous.) So P could be traversed by a dog’s kind of invisible fence—one that feels substantial to us dogs. 🙂I think Dick and I pretty much agree with your statement that belief in P != NP is analogous to belief in the Riemann Hypothesis, but at different levels—he also shares more of Turing’s skepticism about Riemann. Anyway, we tried to engage the issues more substantially here.
Any reasonable person can see that the strong bias against believing NP=P is the main difficulty in resolving P vs. NP issue. Why one would not consider even the possibility that NP=P? This reminds me the quote of Max Planck:
“A new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die, and a new generation grows up that is familiar with it.”
How many generations this resolution is going to take?
The barriers against proving P!=NP of relativization and natural proofs seem to me to be exceptionally strong. Vast swaths of proofs have been ruled out. As for the other possibility, we have scarcely scratched the surface of possible algorithms.
Anyone who believes that P=NP might be possible has a much easier target to aim at: Disprove the Strong Exponential Time Hypothesis (SETH)! That is, find any algorithm that solves CNF-SAT in 2n – ε n time. This is required in order to bring P=NP even into the realm of possibility. We don’t even have a randomized algorithm this good.
It is an open question even to beat 2n – O(n/k) for k-SAT. I expect that beating this latter bound is possible, but this is the limit of all our current techniques.
These are not neglected problems; many serious researchers are looking at them!
Moreover, recent work in fine-grained complexity has shown that polynomial improvements in any of a host of polynomial-time problems, including edit distance and LCS and many other simpler problems, are automatically improvements in SAT algorithms. In other words, many researchers who didn’t realize that they were unsuccessfully trying to improve SAT algorithms, actually were doing so.
I personally am uncertain about whether to believe that SETH is true or not, but the Exponential Time Hypothesis (ETH), which rules out 2o(n) time algorithms for SAT and is still a huge strengthening of P != NP, seems very plausible.
The preprocessor ignored my commands so those should be 2^(n-ε n), 2^(n-O(n/k)), and 2^(o(n)) bounds
Thanks. One thing to add is that getting 2^{o(n)} for SAT (maybe together with something else) could already imply nonlinear circuit lower bounds, so what would getting 2^{O(log n)} for SAT do…
Dear Paul, are there analogous statements (perhaps even stronger but still unknown) to SETH higher up in the polynomial hierarchy? Namely you look at a computational task in the 7th level (say) that admit an easy algorithm with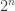
steps and you want to show you cannot solve it with 
steps even if you can call an oracle for a computational task in the 6th level. Anyway, the question if we can hace stronger and stronger variants of SETH untill reaching something which is false in an interesting way…
It was fun to be a part of this panel! My comment about “banging rocks together” was said in regard to problems such as P versus NP. There are many other problems for which aren’t in the stone age 🙂
Gil, it’s not clear to me that what you’re posing is a stronger variant of SETH.
One definite way of weakening SETH would be to strengthen only the algorithm model (rather than also strengthening the problem to be solved). There is a Nondeterministic SETH (NSETH) posed by Carmosino et al. (ITCS 2016) which is stronger: can one prove the unsatisfiability of a CNF with 2^{(1-eps)n}-length proofs checkable in 2^{(1-eps)n}-time? The still-stronger Merlin-Arthur SETH (MASETH) with probabilistic proofs is known to be false (in CCC 2016).
There has been work on stronger versions of SETH that has led to a level at which it is false in an interesting way but not in the way you suggest: Carmosino et al in a 2015 ITCS paper introduced a nondeterministic version of the hypothesis NSETH (that proofs of unsatisfiability much shorter than the obvious ones do not exist in general), and showed that it would have interesting consequences. They also introduced the possibility of AM or MA versions, but Ryan Williams in a CCC 2016 paper showed that AM-SETH (and AM-SETH) are actually false.
thx for your “devils advocacy”/ going out on a limb (over the years) of P vs NP and P=NP, one of my favorite topics! found it myself in the early 1990s. the problem is verging on its 50yr anniversary, hope that there is some celebration at that time. & amusing/ highlight to see SA in the comments & his recent survey is a real milestone on the subj. also like your tying in SAT a lot to your blog over the years & its connections to P vs NP. a suggestion, think that transition point/ physics angle on P vs NP is quite significant; there was a recent high voted SE question on that.
http://cstheory.stackexchange.com/questions/37382/did-where-the-really-hard-problems-are-hold-up-what-are-current-ideas-on-the
more (“devils advocacy”) on P vs NP!
https://vzn1.wordpress.com/category/p-vs-np/
You write there are some new ideas needed on $P \neq NP$. Are there questions from other areas of mathematics (set theory, graph theory, order theory,…) that could give an answer on P vs NP? If yes, a blog post on this would be highly appreciated.
To prove p != NP, first prove PSpace != P. Slightly involved, since there always exists a large monotone boolean formula Q on N variables that “decides” all 2^N QBFs of the original boolean formula R.
I would start with the idea that formula Q is often exponential, thereby showing you cannot decide All QBFs of R in P. Then just show that deciding one QBF is not in P 🙂
The equivalence that the number of valid quantifications of a formula equals the number of satisfying assignments of the formula is also surely interesting.
Dear Colleagues,
In this preprint I show that the problem of determining if a given state is entangled or separable is at least as hard as the hardest problems in NP.
https://arxiv.org/abs/1609.01541
And to show this I present a proof of the existence of a one-way permutation that cannot be inverted in subexponential time in the worst case. I also show that the hard-core predicate of the one-way permutation is a EPR pair.
I am available to debate if anybody is seriously interested in the relationship of quantum computing and P versus NP.
AdC
Has there been any progress in showing that generating a clause of length k is more than just “similar” to solving a qbf on n-k variables? In my experience, the word “similar” could be practically replaced by “equivalent”, which would show NP=Pspace. Needs strong theoretical exploration, imo, as a longtime satisfiability programmer.
And, in my previous post, the large monotone boolean formula Q that decides All 2^n QBFs of formula R is almost always exponentially sized (if R is monotone, then it is equivalent to Q except that in Q, the semantics of the variables are higher level). So evaluating the decision for a qbf by evaluating an assignment in Q is also exponential. This is strong evidence that deciding qbfs is exponential, but I am not sure how strong…
Suffice it to say, proving P!=NP may have to descend from above NP to succeed. I am a strong believer that NP=PSpace=Exp.
Try coloring degree nine regular graphs with four colors and two hundred vertices, a high percentage of which are satisfiable, and you may agree. They take weeks of cpu time for a good solver. That is called the C4D9 “hard spot”.
At the end of Scott Aaronson’s survey, he mentions the idea of using massive computer search. As people have mentioned (e.g. Scott’s post http://www.scottaaronson.com/blog/?p=122, “8. The Self-Referential Argument”), if it were easy to solve NP problems, then we could code up SAT solving, as a SAT instance, and easily solve it…
One idea might be to use a SAT solver to find the fastest SAT-solving circuit for, say, five variables. Then use that circuit in your SAT solver, to look for the fastest circuit for ten variables. (At the simplest level, you could use the DPLL SAT algorithm until you got down to five variables, and then use the circuit you found). Lather, rinse, repeat…
Since my guess is that P!=NP, I expect this would get difficult, fast. However, at every step, you’d be at least partly using an optimal algorithm.
There are a few nice things about this. One is that, for tiny problem sizes, you can graph what the actual circuit size needed to solve SAT is. (I realize that even if the graph starts out looking, say, exponential, when n is small, that doesn’t prove anything.) A nice side effect, though, is that you get the best circuit to solve SAT (admittedly, for tiny problems).
I was a little obsessed with figuring out how hard triangle-detection was, for some time. So I threw together some code to use a SAT solver to look for triangle-detecting circuits, at
https://github.com/joshtburdick/tribound . This might be a starting point for someone to do this SAT search, although the code is admittedly a bit hacky in places, so if you do this, it might be better to start from scratch.
Is it possible while believing in P is not equal to NP, (accidentally) finding an efficient algorithm for the solution of a NP-complete problem?
Yes, and the other way around too! 🙂
By the way, if someone out here could show that all proofs of P!=NP are impossible to communicate… $1,000,000 at stake!
I was working on selective combinatorics, the formula of which I thought could lead to an algorithm that solves efficiently NP-Hard problems.
After writing the formula down my belief of was strongly shaken, I turned to set theory and worked on selective incompatibility seeing it as a fundamental work that must be precede every selectivity work.
I found P to be distinct from NP.
I strongly believe P!=NP, NP=PSpace-hard, PSpace=Exp, and yet I produced a table of Golden Points for regular graph coloring. To produce the table, I generated N random instances of the given type of graph coloring problem, all of which were satisfiable. The High Probability (1 – 1/N) golden coloring points are:
C3D5N180 C4D6N18 C4D7N35 C4D8N60 C4D9N180? C5D10N25 C5D11N42 C5D12N72
The C4D9 point is tentative, and probably low. The rest of the regular graph coloring points were fairly easy to find. My 25 year old solver is fairly efficient, and can solve over one hundred thousand instances in a single file.
Here is a lamb to be slaughtered…or revered.
Why I believe NP=Exp
+++ Sketch of why I believe PSpace=Exp
AllQBFs is the problem of constructing a boolean expression Q that
decides all 2^N quantifications of an original boolean expression R,
by plugging in T for existentially quantified variables and NIL for
universally quantified variables, then evaluating Q. Clearly, Q could
be constructed in a slow doubly exponential way by deciding all 2^N
quantifications of R using your favorite qbf solver, then building Q out
of all the satisfying quantifications. But there is a much more clever
method, singly exponential, using the tree of satisfying assignments to R.
The tree of satisfying assignments is ordered with the first variable at
the root, and the nth variable at the leafs. Recursive apply a set union/set
intersection procedure to the tree, beginning at the root. First, apply the
procedure to each branch of the root, then place the union of the leafs
of the two branches on the left branch, and the intersection on the right
branch. The resulting tree then has a monotone clausal form. Each clause
is essentially a minimal set of jointly unsatisfiable universal constraints. So
a clause (x1 x2 x3) means x1 x2 and x3 canot all be simultaneously universal
in a valid quantifiction.
There are usually an exponential number of clauses in Q. Evaluating a
qbf S of R requires examination of all clauses that contain any subset of
the universals of S; that is often exponential. If some clause of Q contains
only universals of S, then quantification S is invalid. If all clauses in Q
containing some universals of S also have an existential variable of S
then S is valid.
We can prove by contradiction that to verify S, “usually” an exponential
number of clauses of Q must be examined. I believe this means that QBF
must usually be exponential, and thus PSpace = Exp.
+++ Sketch of why I believe NP=PSpace-hard
My other reasoning is about NP. Current satisfiability solver methods
involve discovering and adding length k clauses, which is similar to solving (n-k) qbfs.
To me, that means current methods are PSpace-hard, but this is not yet a proof
that NP is PSpace-hard.
I am unable to see weak spots. Anyone care to point them out?
Daniel Pehoushek
The paper, “Introduction to QSpace”, published at the International Workshop on QBFs, at Satisfiability 2002, can be found at:
gauss.ececs.uc.edu/Workshops/SAT/Abstracts/QBF/pehoushek.ps
Yes, I had “AllQBFs” in 1997, published in 2002, but have gotten the null response ever since. My credentials are good, GRE scores nearly perfect, former PHD student at Stanford CS, discovered numerous other things, including an O(N/M logM) average case string matching algorithm good on binary alphabets too. I have worked on satisfiability for over 25 years. Most recently, I have isolated a hard spot for regular graph coloring of ninth degree graphs, at C4D9N>=180. But the sketch above is probably my best result, tending to show QBF evaluation must be exponential, because there are an exponential number of constraints in formula Q that must be examined, or else an adversary can ruin the validation.
I have an AllQBFs.cpp program, and I am willing to share. I also have a random graph generator. I have run the AllQBFs program on several of the regular graph Golden Points files. The output on C3D5N180 is about 1 Gigabyte per formula… The program produces Q formulas, boolean formulas that decide all qbfs of the original formula. I am preparing an AllQBFs paper for SAT17.
If anyone has a boolean formula, in dimacs cnf form, and wants to know which of the 2^n qbfs are valid, just send me the formula, I will send you the Q formula. Or, I can send you the program…
Here is the beginning and ending of a 27 million line Q formula
for 3 coloring the first 180 vertex graph in my files.
The first line means that variables 1, 2,3,4 in the coloring
formula cannot all be universally quantified in any valid quantification.
[ begin C3D5N180high.veg file number 1 ]
[ 1 ( n 360 m 1536 )( bags 541 om 1441 ( h 24 m 3060 ) ) :(5 0 0 1 6 2 180 3 0 4 1350 ):
p all 360 27172344
1 2 3 4
1 2 3 5 6
1 2 3 5 7 8
1 2 3 5 7 9
1 2 3 5 7 10
1 2 3 5 7 11
1 2 3 5 7 12
1 2 3 5 7 13
1 2 3 5 7 14
1 2 3 5 7 15 16
……
348 349
348 350
348 351
348 352
348 353
348 354
348 355
348 356
348 357
348 358
348 359
348 360
349
350
351
352
353
354
355
356
357
358
359
360
Here is a relatively long Q clause near
the beginning of the 27 million line monotone cnf.
It means that in any valid quantification, at least
one of these fifteen variables must be existentially
quantified. The other fourteen could be validly
universally quantified… I have not found the
longest clause yet.
1 2 5 6 7 20 47 85 87 97 98 152 197 355 360
Here is a sequence of nine clauses, each 24 variables, where one of the
variables must be existential in any valid quantification…
still near the beginning of the 27M line Q formula.
You get the idea. Q formulas can get large, but they are
useful for deciding any of 2^N qbfs of the original form.
…
1 2 6 7 9 11 15 18 20 38 72 114 123 138 140 168 174 188 190 197 258 286 351 352
1 2 6 7 9 11 15 18 20 38 72 114 123 138 140 168 174 188 190 197 258 286 351 353
1 2 6 7 9 11 15 18 20 38 72 114 123 138 140 168 174 188 190 197 258 286 351 354
1 2 6 7 9 11 15 18 20 38 72 114 123 138 140 168 174 188 190 197 258 286 351 355
1 2 6 7 9 11 15 18 20 38 72 114 123 138 140 168 174 188 190 197 258 286 351 356
1 2 6 7 9 11 15 18 20 38 72 114 123 138 140 168 174 188 190 197 258 286 351 357
1 2 6 7 9 11 15 18 20 38 72 114 123 138 140 168 174 188 190 197 258 286 351 358
1 2 6 7 9 11 15 18 20 38 72 114 123 138 140 168 174 188 190 197 258 286 351 359
1 2 6 7 9 11 15 18 20 38 72 114 123 138 140 168 174 188 190 197 258 286 351 360
…
Ooops. After removing subsumed clauses, the number of clauses in the Q formula dropped way down, to 346290. There are still some long clauses, which describe some very difficult constraints to validate any other way.
more oops. thats life.
after properly removing subsumed clauses,
the Q formula that decides all 2^ qbfs reduces to
a nearly linear sized formula.
I retract all claims about pspace=exp for now.
Presently, constructing a Q formula requires
processing the satifiability tree, so they are
pretty hard to make…
Here is the Q formula that decides 2^n qbfs of
a 3 coloring problem on a 360 variable 180
vertex degree 5 problem. A lot of variables
must be existentially quantified in a valid
quantification.
++++++++++++++++++++++++++++++++++++++++++++++
[ begin first.veg file number 1 ]
[ 1 ( n 360 m 1536 )( bags 541 om 1441 ( h 24 m 3060 ) )
p all 360 476
1 3 5 6
1 3 5 7
1 3 5 8
1 3 9
1 4
1 6 8
1 7 8
1 7 9
1 10
1 14
1 23
1 26
1 32
1 57
1 76
1 78
1 85
1 175
1 291
1 348
2 3 5
2 3 6
2 3 9
2 4 5 6
2 7
2 8
2 10
2 14
2 23
2 26
2 32
2 57
2 76
2 78
2 85
2 175
2 291
2 348
3 4 5 6
3 4 8 10
3 4 10 14
3 5 7 8
3 6 7
3 6 8
3 6 9
3 6 85
3 7 8 78
3 7 10
3 23
3 26
3 32
3 76
3 291
3 348
4 5 6 7
4 7 10
4 7 76
4 9
4 14 76
4 23
4 32
4 57
4 78
4 85
4 175
4 291
4 348
5 6 8
5 7 291
5 9
5 10
5 14
5 23
5 26
5 32
5 57
5 76
5 78
5 85
5 175
5 348
6 7 8
6 7 9
6 7 85
6 10
6 14
6 23
6 26
6 32
6 57
6 76
6 78
6 175
6 291
6 348
7 8 10
7 9 291
7 14
7 32
8 9
8 14
8 23
8 26
8 32
8 57
8 76
8 85
8 175
8 291
8 348
9 10
9 14
9 23
9 26
9 32
9 57
9 76
9 78
9 85
9 175
9 348
10 23
10 26
10 32
10 57
10 76
10 78
10 85
10 175
10 291
10 348
11
12
13
14 26
14 32
15
16
17
18
19
20
21
22
23 78
24
25
26 32
27
28
29
30
31
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76 348
77
78 85
79
80
81
82
83
84
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
292
293
294
295
296
297
298
299
300
301
302
303
304
305
306
307
308
309
310
311
312
313
314
315
316
317
318
319
320
321
322
323
324
325
326
327
328
329
330
331
332
333
334
335
336
337
338
339
340
341
342
343
344
345
346
347
349
350
351
352
353
354
355
356
357
358
359
360
+ #P 300263 = #Q 300263 retros 107344 oh 34499172 ttt one ]
It might also be interesting to investigate obstacles to proving P = NP. Along these lines, I was able to construct a counterexample which eliminates a number of commonly proposed approaches to proving that P = NP from consideration. If one allows proof techniques of the sort used to prove the four-color map theorem, one can go further and show that NP is not contained in P. A preprint developing these ideas is available at https://fermatsociety.files.wordpress.com/2017/02/np-is-not-contained-in-p.pdf
In general, UP vs NP is a completely different problem than P vs. NP. In particular, while a strong connection of NP and (promise) UP is already known, P is widely believed to be different than NP. We define a problem that we call General Quadratic Congruences. We show General Quadratic Congruences is an NP-complete problem. Moreover, we prove General Quadratic Congruences is also in UP. In this way, we demonstrate that UP = NP.
https://hal.archives-ouvertes.fr/hal-01304025v6/document
and I’m very late for the panel questions. I have a conjecture that all those people in the panel, and all in the Paul Beame thread are the manifestation of the possibility of P=NP or even stronger statement. So, the question for the panel is whether we can experimentally prove that those (or any other) physical devices are not capable of performing non-deterministic computation efficiently? I’m serious. I’ll run experiments if we can find experimental paradigm. We do have experimental devices, and no one is asking experimental questions.
——— The following is not serious, but “good mathematicians looks for the analogies between analogies”, and human brain is associative, may be it will trigger something in non-deterministic brains ———–
The P vs NP is the problem of checking many inputs on the same piece of hardware at the same time. For example, if we would be able to implement NAND as a linear computation, than one can implement the Boolean satisfability by creating a vector representing a superposition of all possible inputs. Than, because, each vector in the superposition is representing possible input each of those inputs will be evaluating to 0 or 1 depending on the satisfability of the particular input. The evaluation of the formula on the superposition vector would lead to the number of inputs evaluating at true. If this fantastic scenario would be possible that would show P# = P. which is much stronger. The problem is that the input is in the plain.
But that is also give an idea where to look at. The trues table of NAND or NOR have 3 equal output and one different, that can be represented as a pyramid, with 3 inputs corresponding to the same output being at the base, and another one at apex. To do this one need to keep track of all 4 inputs, that will lie in 2D, and augment all the inputs with correct value of the third dimension. Basically, all 4 inputs are projected to 2D space, than some of them are augmented with 3rd dimension and projected back to the original space. — no details — we want to sort all the inputs linking (“entangling”) them by the augmented spaces via projections, repeating this operation for each NAND gate. At the end we need to check whether the specific subspace is empty for P=NP, or the number of vectors (may be the norm of superposition of back projected vectors) for P#=NP.
And this is not a proof, this is a crackpot’s drivel.
I don’t believe P vs NP to be set theory independent, in the contrary I think set theory is the answer.
I invite you to read this paper I wrote
https://drive.google.com/file/d/0B2iY_1VArjmYTUttR1h5WTRIWDg/view?usp=drivesdk
I don’t believe P vs NP to be set theory independent, in the contrary I think set theory is the answer.
I invite you to read this paper I wrote
https://drive.google.com/file/d/0B2iY_1VArjmYTUttR1h5WTRIWDg/view?usp=drivesdk
Note to moderator, only the lastest comment contains a functional link.
“Genius is one percent inspiration, ninety-nine percent perspiration.”
― Thomas A. Edison