Reading Into Atiyah’s Proof
The Todd function method

|
| MacTutor biography source |
John Todd was a British geometer who worked at Cambridge for most of his life. Michael Atiyah took classes from him there. He was not Atiyah’s doctoral advisor—that was William Hodge—but he advised Roger Penrose, Atiyah’s longtime colleague at Oxford.
Today Ken and I want to add to the discussion of Atiyah’s proof of the Riemann Hypothesis (RH).
Primary sources are Atiyah’s short paper and longer precursor, the official video of his talk, and his slides. Discussion started here and has continued in several forums. MathOverflow removed their discussions; apparently so did StackExchange. A number of news sources reflect the universal skepticism.
We will not try to cover the same ground as these discussions, nor enumerate statements about holes in the papers. Instead we have gained some small insights into what Atiyah is doing. We are not disagreeing with the conclusion by many that “it’s not all there” but we think we can identify a few more things that are there—by intent—than we’ve seen noted. They don’t make a proof (either) but we think they are important to understand where all this is coming from, and that such an understanding is warranted. At the very least this is an exercise in how to read a challenging source.
We will first explain a previous proof that uses a related method—a famous proof that works and is correct. Then we will explain Atiyah’s idea as we see it.
The Todd Trick
Atiyah of course is well aware of the classic use of a special function to prove a deep theorem of complex analysis. Let’s call this the “Todd Trick.” The proof uses the existence of a complex function lambda () with certain special properties. Let’s recall the famous Liouville theorem, named after Joseph Liouville:
Theorem 1 Every bounded entire function must be a constant.
Then the famous stronger Picard theorem, named after Émile Picard, states:
Theorem 2 Every entire function that misses two points must be a constant.
Sketch of Proof: Let be an entire function that misses two points, which we may assume are
and
. This follows by using a linear map to move the missed points, if needed. Then the magic is to look at the following function
:
It follows that is a bounded function, since it misses the poles of
. But then we see that
must be a constant and so
is a constant.
The Todd Trick For The Riemann Hypothesis
Atiyah claims to have a proof of the famous RH. It is based on a special function that he calls the Todd function and he denotes it by . The function has a slew of special properties that Atiyah lists. Then he uses the properties to prove the RH directly.
This proof is very much in the spirit of the above proof of the Little Picard Theorem. So there is hope. But we are puzzled over some of the properties that is suppose to have. We must be confused but it seems that
cannot have all the properties that are needed.
Here is the way that we think Atiyah proof is going. Consider the space of complex functions with a power series centered around some fixed point
. Define
This will be our “Todd function.” Note this function is well defined on the given space and satisfies the key property
This explains how it is possible to get
with no higher terms. We use for our version of his function to mark that it is a variation of what he seems to say.
in this form is really an operator as signaled by the use of curly braces in the last equation. Note that its right hand side also equals
. This is the sense we get from two pivotal equations on page 3 of Atiyah’s short paper—where, however, we use curly
not
. The former, to which we’ve added the label ‘(A)’, is said to apply when “
and
are power series with no constant term.”
The reason we use curly is that the only way to make sense of the former equation is to read it as
applied to the functions
and
and
in the form of power series, and then the resulting function or series is applied to the complex number
. It does not make sense to say that for any
we evaluate
and
and then say that the results obey
.
Our point is that the latter equation (3.1) hence needs to be read the same way—not as a simple function value where
. That is, it must be what we are writing as curly-
applied to
as a function—indeed, as a power series. Then the result is applied to
. This is neither hairsplitting nor special pleading but a need we feel as computer theorists who have used strongly-typed programming languages.
This means we want to understand as a power series. No such series appears in the papers, but given Atiyah’s surrounding references to power series it must be there. So we will try our best to supply what is indicated.
Power Series For Zeta and Square Root
A power series for differs from its original summation formula by having
in the bases rather than the exponents. There are several ways to represent
as a power series. Actually, from above we want a series for the function
(to be applied to
), which may or may not have the same effect as the function
with fixed. Since we are not trying to be perfect, we will mention the Laurent series around
as given here:
Here the are constants named for the Dutch mathematician Thomas Stieltjes, except that
is the Euler-Macheroni constant
The next one is
. Expanding the series around
rather than
separates out the pole at
via the first term.
If some particular property of a power series for affects the application
then this insulates against the charge that no special property of
is being used. To be sure, no special property is evident in the papers, and the burden to state one is on the claimer, but an intent along these lines is more likely than a blank slate.
Now the same logic must apply to two numbered equations that appear between the two we juxtaposed in the last section. They are extra-confusing because now “” is written as a simple function without curly braces. Here they are as they appear, including a cryptic “or”:
Which is it, or
? A remark just before these latter two equations hints at the answer “both”:
Remark. Weakly analytic functions have a formal expansion as a power series near the origin. Formula 2.6 is just the linear approximation of this expansion (more precisely this is on the branched double cover of the complex
-plane given by
).
So what is going on involves approximation of a power series. Thus “” must be carrying out a linear approximation of a series. Hence “
” needs to be read this way. It is hard to read the right-hand side of 2.6 and the left-hand side of 2.7 with
inside the square root, but we can use them to substitute:
which per above really means
with a power series for as the argument for
. The Maclaurin series expansion (as given here) is
Taking away the super-linear terms leaves , which by the same intent equals
as stated. That the whole series converges provided
confers some legitimacy.
The Final Line to Read
Here is a screenshot of the climax on page 3:
The key line is the one saying, “Now take in 2.6″—where 2.6 refers not to the equation with that number but to the one we’ve labeled ‘(A)’ which is in paragraph 2.6 of his paper. The important point in this substitution is not that
is a numerical function on
but rather that
is to be treated as “a power series with no constant term.” This means that an application of
is given as argument for another application of
.
We can’t claim to have connected all the dots. We haven’t even connected the factor in
from the square-root expansion (subtracting off the constant term
) to its claimed use to get
. Taken at face value, the latter holding on any open region entails that
must be linear. But connecting more dots helps to see fault lines more clearly, both for Atiyah’s papers and attempts on RH in general.
Still A Problem?
The emphasis on linearity in our exposition sharpens the kind of objection raised by Luboš Motl in his review: Take any two zeroes and
close by each other on the line, take
and
and define:
This exchanges two genuine zeroes of for two mirror-image new zeroes of
that are off the line by
, and likewise for their complex conjugates. We have chosen
and
to minimize the effect on series expansions of
compared to
. Would the discrepancy affect the coefficient
of the new linear term compared to
of the original linear term for
? Surely, not enough is said about what
is in the relevant series to tell, nor about any other way to distinguish
from
. But Motl’s example and our attention to series have at least channeled the question.
There are numerous other issues with the papers. Regarding the assertions about the fine structure constant, perhaps the argument is best left to physicists, but we note a 2010 paper by Giuseppe Dattoli. It is titled, “The Fine Structure Constant and Numerical Alchemy” and gives both a historical survey and a would-be simple formula for it. Both Dattoli and Atiyah have references to Kurt Gödel at the end of their papers. Just before the latter is a sentence that is wrong at face value: “To be explicit, the proof of RH in this paper is by contradiction and this is not accepted as valid in ZF, it does require choice.” On the contrary, RH has purely arithmetic formulations—indeed with only one unbounded quantifier per reference to Jeff Lagarias here—and all arithmetic statements (and more) provable in ZFC are provable in ZF. Nor is “by contradiction” an issue for ZF. Atiyah’s next sentence, however, talks about “most general versions” of RH and his concern about hoice might transfer to them.
Finally, we remind that some key ingredients in the essay on RH by Alain Connes, which we mentioned in the previous post, involve analyzing operators that, like , are idempotent. These have great sophistication. More down-to-earth, a calculation by Ken at the end of this recent post gives a motive for cutting off terms above
where both
and
are small. Those terms don’t vanish in the real world but calculating in spaces where they do vanish may help clarify real behavior of limits involving them.
Open Problems
Is the proof’s idea okay or not? Does have the properties that are claimed? The general idea of a “Todd” approach to the RH seems at least to be an interesting idea. Can we make a list of properties that a function must have to shed light on the RH? Are we right that the Todd function is not defined on complex numbers, but is defined on functions represented by series? The most accessible reference we have found is chapter 5 of this 2004 thesis linked from this StackExchange discussion.
Trackbacks
- Riemann hypothesis, fine structure constant, Todd function
- Has the Riemann hypothesis been proven? | Page 4 | Physics Forums
- Atiyah Riemann Hypothesis proof: final thoughts | The Aperiodical
- Has the Riemann hypothesis been proven? | Page 4 | Physics Forums
- Atiyah Riemann attack/ post mortem/ autopsy, Primes torch carried on | Turing Machine
- 1 – Atiyah Riemann Hypothesis proof: final thoughts | Traffic.Ventures Blog
- Resumen de lecturas compartidas durante septiembre de 2018 | Vestigium
- Reading Into Atiyah’s Proof | Gödel's Lost Letter and P=NP - Nevin Manimala's Blog
- Practical consequences of RH ? | Theresa Welchy
- Practical consequences of RH ? – Site Title
- Jean Bourgain 1954–2018 and Michael Atiyah 1929–2019 | Gödel's Lost Letter and P=NP
- A Prime Breakthrough | Gödel's Lost Letter and P=NP



My understanding of the reference to Choice is that the Todd function is not constructively defined, but is shown to exist, being a composition of two transformations that can be shown to exist.
I have not read you post yet, but I really do appreciate that you take Atyiah serious. I have worked multiple times with “old people” in my job(s) (and privately), and found that they can really work hard and add value, even if they develop (sort of psychological) traits beyond my understanding (and probably beyond the understanding of most young people). Example of a “trait beyond my understanding” : an old colleague proposed an unsuitable method to solve a problem. He estimated its runtime, and at some time got a negative number. He then proudly presented that negative runtime estimate as an argument in favour of his method.
Section 3.4 in the longer paper says explicitly that T maps complex numbers to complex numbers, though I agree that if that’s the case, nothing seems to make much sense.
It’s very strange reading the papers. If everything is taken literally, the papers are full of elementary mistakes. On the other hand, it feels like there could be some kind of interesting idea, if one somehow gets through the extremely vague and confusing writing.
its a wild goose chase.
reading Atiyahs extraordinary biography on wikipedia. his wife died at age 90 about ½yr ago,
march this year. maybe/ presumably having some major impact on his life.
he doesnt seem to have much published physics papers. some of his abstract math ideas on gauge theory were imported by witten. hes won at least 1 math award, not sure what it was for. (the President’s Medal from the Institute of Physics in 2008,)
“This resulted in a series of papers on spectral asymmetry,[75] which were later unexpectedly used in theoretical physics, in particular in Witten’s work on anomalies.”
“Atiyah and Singer found that anomalies in quantum field theory could be interpreted in terms of index theory of the Dirac operator;[102] this idea later became widely used by physicists.”
he has a huge list of prizes. wonder if he is going to receive any more.
like that his work touches on instantons, a form of soliton— this is the future of physics. bohmian mechanics → pilot wave hydrodynamics → fluid mechanics
https://vzn1.wordpress.com/2018/09/26/atiyah-riemann-attack-post-mortem-autopsy-primes-torch-carried-on/
He has won a Fields medal *and* the Abel prize! Very few mathematicians (Wiles) have won both. As for his “math” contributions, the Atiyah-Singer theorem comes to mind. That’s not the point of the discussion here, however.
😳 hi all accidentally quoted this misinfo on my blog (lol was thinking on writing it that it was amazing/ news to me + surprised to have not heard!) and SE mathoverflow mod Todd Trimble was very helpful in doing fact checking/ quickly relaying correction. Wiles did not win Fields medal. these seem to be the only living mathematicians who have won both Fields medal + Abel prize. Atiyah, John Milnor, and also Jean-Pierre Serre, John G. Thompson (the group theorist of Feit-Thompson fame), and Pierre Deligne. https://vzn1.wordpress.com/2018/09/26/atiyah-riemann-attack-post-mortem-autopsy-primes-torch-carried-on/comment-page-1/#comment-8018
I looked at Atiyah’s preprint on the fine structure constant https://drive.google.com/file/d/1WPsVhtBQmdgQl25_evlGQ1mmTQE0Ww4a/view
which purports to give a way to calculate it to arbitrary precision. I was unable to reconstruct or reproduce his calculation, or even to understand quite what he is doing. Has anyone been able to reproduce this part of his work?
Minor point:
After equation 3.3, F(s) = 2 F(s), the comment about C not having
characteristic 2 is irrelevant (x = 2x implies x=0 in any characteristic).
This is a very minor detail, but still, such details are rarely overlooked in regular math papers.
True, but comparing this with the slide show, there appears to be a typo as that instead has F(2s) = 2F(s). The statement about characteristic 0 suggests that the line we are looking for is actually 0 = 2F(s).
Terry Tao looks like he is going ahead with his number crunching for RH. So Terry cannot be looking for a second attempt that falls short of great proof of Atiyah.
❗ 💡 :star: 😎 <3 thx for the great tip its fantastic/ exciting/ exhilarating to see that tao is looking very deeply into numerical approaches to RH/ number theory, have been getting flamed in my own blog by multiple trolls for similar approaches on collatz. looking at his apparently latest post on the topic, he has some brief comments on Atiyah attack. https://terrytao.wordpress.com/2018/09/06/polymath15-tenth-thread-numerics-update/
:star: liked it so much decided to publicize it and reddit math likes it too. more on Terence Taos serious/ credible/ highly researched/ collaborative etc approach vs Riemann on reddit. RJL itd be great if you looked into it at length and blogged on it (instead!). think it sure beats what everyone else got sidetracked by, the shiny bright object lying by the side of the road. https://www.reddit.com/r/math/comments/9jy1ai/terence_tao_vs_riemann_hypothesis_polymath_15/
another thought… btw RJL you guys do the best job of nearly anyone of taking new proof attempts seriously/ respectfully as possible going back to deolalikar and Blum, and thats a fabulous and at-times thankless scientific/ public service, have real gratitude for that, but this approach is ofc prone to false positives. rereading, this statement sticks out and it seems even with your earlier qualifications, there is some element of denial going on… “We must be confused but it seems that {T} cannot have all the properties that are needed.” without being near to the details (maybe an advantage in this case) consider: no, the simplest explanation is that Atiyah is “confused”. that is the report of multiple reviewers/ insiders. you skipped the mention that hes ALSO circulating a 12 page proof of Feit-Thompson mentioned in the news article (didnt hear about that either until you cited that article, thx for that!). incl 6-spheres attack, this is the 3rd time hes cried wolf in year it would seem. fool me once, shame on you, fool me twice, shame on me, 3 times fooled, shame on everyone. the news articles only delicately hint at his mental condition but if this continues it will be more pronounced, and maybe theres going to be a garish tabloid story showing up on him soon (but telling the bitter truth, sometimes a hard pill to swallow) like what happened for Perelman… maybe just a matter of time…
Are you claiming that a “garish tabloid story” about Perelman was actually the bitter truth? I read a book whose author seemed to be trying to explain Perelman’s behavior as the result of a possible mental illness, but it is not clear why the author dismissed his claims of having specific moral views. Such moral views (about the behaviors of many of the people in the academic world) could explain his behavior, so why did the author posit mental illness? Is there additional evidence I missed?
holy cow someone with a real name commented? stop the presses! perelman is a whole other case and maybe will do a blog on him sometime, never wrote one yet, have alluded to him a few times. another way of looking at it is that most tabloids are garish and almost anything they write has a garish sheen, and yes a few tabloids wrote about perelman. which book are you talking about? have read one by gessen that is very well researched, have been citing it on reddit lately. anyway try reading this tabloid story and see how garish you think it is. if its not garish enough, will dig up others more garish. (maybe garish is not the perfect adjective here anyway.) perelman is eccentric to say the least, anyone would agree with that. yes, speculating about others mental illnesses is total landmine territory. but there are statistics that nearly 25% of population has mental illness at some point in their lives… its a fact of life in this world. how do we deal with it like adults? https://www.dailymail.co.uk/news/article-1259863/Worlds-cleverest-man-turns-1million-prize-solving-mathematics-greatest-puzzles.html
“holy cow someone with a real name commented?” Well, I AM a Mannian Democrat, after all.
I think it was that book by Gessen that quoted Perelman’s reasons for not accepting the million dollar prize, and then implied that only someone with a mental illness would refuse a million dollars. He said he does math to expand humanity’s knowledge, not for fame or fortune. People who hear that and say, “Yeah, right. But what’s the real reason?” are revealing something about themselves. (Don’t get me started on people who say he should have accepted the money and given it to charity.) I’ve dreamed of making big contributions to society and then turning down awards on big stages since I was little.
He was also criticizing the behaviors he witnessed by other academics and the media. I forgot the details, but one of his claims was that a group of mathematicians at his university accepted money for work they didn’t do and split it amongst themselves. Because he was part of that group, he got a piece of that money. He demanded that they take the money back and leave him out of it. He seems to have a moral view against greed and corruption. People who hear that and say, “Yeah, right. But what’s the real reason he gave the money back?” are revealing something about themselves. I would have done the same thing.
That article implies his apartment has roaches, but that’s irrelevant information. Yes, I am introverted. Yes, I do have strong moral views about how people should behave. But does that mean I am eccentric or mentally ill? You seem to lean towards believing Perelman has a kind of mental illness that would explain his refusal of money. If so, why?
You could see my proof of UP=NP in
https://www.academia.edu/37430336/UP_versus_NP
and see my proof of P = NP in
https://www.academia.edu/37469408/P_versus_NP
Thanks in advance…
Sorry, I can’t quite seem to follow all of the arguments in the section on “Todd trick for RH”. Assuming you specialize to a = 1 in the 3rd equation, how exactly do the terms involving f'(1) and g'(1) disappear?
Also, what do you mean when you say the right side equals 𝓣{1 + f(z) + g(z)}(1)? 𝓣 is defined as a function from analytic functions to complex numbers, but you seem to be suggesting that we evaluate the result of 𝓣{…} (a number) at 1.
Hello everyone. I’m not a mathematician, I’m just an amateur friend of HR. I felt very happy when I learned about Atiya’s tests, and a little sad now. I had been reading and watching RH videos for the last two years, as entertainment. I like the idea of a simple test, and the idea of a functions function, relational with the exponential function. I like the possibility of a test by contradiction, with an unknown function that says nothing about the meaning of zeros and cousins, but you can say that all zeros are in line 1/2. On this possibility, I have been reading about the Theory of Order and I think we can relate this theory to the RH. Somebody made it? We can say that the minimum of the function, when the values are zeros, are always in the critical line using the Theory of the order, although we do not know why or where is a zero. That is another question. My best wishes to Michael Atiyah. Thank you.
Q: D: I’m sorry if my comment is not appropriate.
Ken,
Apologies for this. As I am not sure of the flavor of latex here at your place, I would like to test if the wrapping tags are $x^2$ or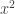 or something else. If you can kindly give a specification at your convenience, I would appreciate it. Thanks
or something else. If you can kindly give a specification at your convenience, I would appreciate it. Thanks
Ken,
It shows and I now know. You may delete the annoyances. Thanks.
This Is Only A Test
Under the distortive force of the colliding tectonic plates of and
and  , the impressively rugged terrain seems to have distracted Riemann’s view. Therefore, the beyond-sight plane
, the impressively rugged terrain seems to have distracted Riemann’s view. Therefore, the beyond-sight plane  was likely the exact reason for Littlewood to leave behind that totally dismissive conviction of the tricks, including all those invented after September 6, 1977. It is actually the only belief, conversely echoed in a non-conventional way by Peter Collins, that makes perfect sense.
was likely the exact reason for Littlewood to leave behind that totally dismissive conviction of the tricks, including all those invented after September 6, 1977. It is actually the only belief, conversely echoed in a non-conventional way by Peter Collins, that makes perfect sense.
3 is still too big a number, isn’t it? Replace it with 1.
After all, is the system identity for
is the system identity for  .
.
Given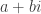 and
and  , can we always find a “middle” vector
, can we always find a “middle” vector  ?
?
Uptodate modern mathematics has it that and
and  are the most unfamiliar and confusing notations ever used. And four is enough to send us out of our wits.
are the most unfamiliar and confusing notations ever used. And four is enough to send us out of our wits.
gets us what?
(If by now the reader already has the answer, the rest can be skipped.)
Does this parse?
gets us what?
I’ve invented a new class of optimization: Complex Programming:
http://vixra.org/abs/1810.0073
Atiyah’s proof is like the Captain of a ship spotting an iceberg through the port window. At least his crew is taking note, and hopefully considering what is beneath the icy depths.
Reblogged this on KEŞKÜL-İ FIKARÂ and commented:
Riemann Hipotezi’nin Atiyah isbatı üzerine okuduğum en ciddi yazılardan biri.
Se could to think that the Todd s functions and fine structure constant are brasis to all the universal functions.How rhe zeros of the function of zeta as well as the the zeros trivial or holes are linked to the pattern followed by the prime Numbers ,linking to the imaginary and complex Numbers that create not lineR sequences
I think that the todd’s function and Fine structure constant are intrinsically linked to the universal laws.i think that function zeta of riemann is linked to the pattern of sequences of prime Numbers só as the existence of complex Numbers that are irracional and transcendental numbersThe way of Atiyah is correct
Is possible algo that the riemann ‘ hipothesis be erógeno Then the zeros non trivial of the zeta ‘s functions is not represent any real Numbers,are justo imaginary Numbers ,that charectize the pattern of distributions of prime Numbers.not represent the continuum of the real space,But yes are represented by the imaginary with non linear shapes measured by the coordenate Time,that is motion of the provesses of the Nature connecteds to the imaginary Numbers or imaginary coordinates as the einstennian spacetime and linked by the PT symmetry or non hermitian hamiltonian functions that is the generalized complex manifolds
Physics and mathematica Giana michael Atiyah debate .this impactes the the mathematicians
https://www.reddit.com/r/compsci/comments/agu5dg/requestreview_for_p_versus_np_paper/