John Horton Conway 1937–2020
An appreciation

|
| Names for large numbers source |
John Horton Conway just passed away from complications of COVID-19. We are all saddened by this news, and we hope you all are doing your best to stay safe and help others cope.
Today Ken and I thought we would reflect on some of Conway’s many contributions and emphasize three in which we see connections to computational complexity.
Conway was a Fellow of the Royal Society, and was the first recipient of the London Mathematical Society’s Pólya Prize. His nomination to the Royal Society reads:
A versatile mathematician who combines a deep combinatorial insight with algebraic virtuosity, particularly in the construction and manipulation of “off-beat” algebraic structures which illuminate a wide variety of problems in completely unexpected ways. He has made distinguished contributions to the theory of finite groups, to the theory of knots, to mathematical logic (both set theory and automata theory) and to the theory of games (as also to its practice).
A Life Force
Conway may be most noted for his game of Life. This is a two-dimensional cellular automaton. Conway invented it in 1970, which he rounded up from 1969. The game—and Martin Gardner’s 1970 column on it in Scientific American—made him famous in the wider community. The website conwaylife.com and several others link to more information than we could digest in a lifetime.
We want to emphasize instead how Conway was a special force in mathematics. He applied an almost elementary approach to deep hard problems of mathematics. This is a unique combination. There have been mathematicians who worked on deep problems and also on recreational math, but few who established integral flows across the boundary between them. Conway infused both with magic in a way conveyed by an iconic photograph of his Princeton office in 1993:

|
| Guardian via Dith Pran, NY Times source |
What Ken remembers is how accessible Conway was outside his office. “I know I met him at least once while I was an undergraduate at Princeton in 1979 or 1980, though this is overlaid by a memory of finding just him and a few others in the Fine Hall tea room when I was there for my tenth reunion in 1991. My most evocative memory is when Conway gave an evening talk to the undergraduate mathematics club at Oxford when I was there sometime after 1981. It was relatively sparsely attended, perhaps because it was literally a dark and stormy winter night. But after his lecture we all got to huddle around him for another hour in the tea room as he regaled us with stories and mathematical problems.”
We also remember that Conway was one of Andrew Wiles’s main confidants during the months before Wiles announced his proof of Fermat’s Last Theorem in June 1993. Here is a transcript of a PBS Nova documentary on the proof in which Conway appears prominently. Ken has picked out two of Conway’s other contributions that we feel may have untapped use for research in complexity theory.
Conway’s Numbers
One of this blog’s “invariants” is first-name last-name style, thus “Godfrey Hardy” not “G.H. Hardy.” But we make an exception in Conway’s case. Partly this owes to how his initials were amplified by Donald Knuth in his novella Surreal Numbers:
In the beginning, everything was void, and J.H.W.H. Conway began to create numbers.
Besides the void (that is, ), the creation uses the idea of a left set
and a right set
. Every number has the form
. The initial number is
Once a number is generated, it can be in the or
of other numbers. Thus, next come
You might think of next, but it violates the invariant
which defines an form to be a number.
The relation is inductively defined for
and
by
That is, no member of the left-set of “bumps”
(in the sense of rowing races) and
does not bump any member of the right-set of
. Note that
and
are not involved—they already behave correctly owing to the invariant. The numbers
are equal if
and
both hold. The rule for addition is
where and so on. The logical rule
for any
makes the definition of addition well-founded. This yields the numerical fact
It is immediate that is commutative. There is also a rule for multiplication but addition gives us enough to talk about here.
Redundancy and Simplicity
It is straightforward to compute that and
. Now consider:
This is a legal number. You can check that the relations and
both hold. Thus—as a number rather than a “form”—the number
equals
.
That seems to make sense since is the average of
and
, but now compute
as a formal Conway number and consider
. This also satisfies the relations
and
, so
must likewise equal
. Thus
is not some kind of numerical interpolation between
and
. The interpretation that grabbed my imagination as a teenager in 1976 is that:
equals the simplest number that is between
and
.
This is especially evocative in cases like , which is what one gets by computing
. In general,
is the simplest number between
and
. Conway made this a theorem by giving each number a set-theoretic ordinal for its “time of generation” and proved that
always equals a (the) least-ordinal number
such that
for every
and
.
Conway’s rules allow and
to be infinite sets—any sets of numbers built by the rules of set theory. Then not only do all real numbers emerge at ordinal times, so do infinitesimals and further richness of structure. We should remember that Conway began as a set theorist with a dissertation under Harold Davenport titled Homogeneous ordered sets. All Conway numbers with finite creation times are dyadic rational numbers, which may seem trivial from the standpoint of set theory, but those are akin to binary strings.
What became magic was how Conway’s rules characterize games. Through games we can also interpret forms like that are not numbers. I did not know about complexity when I purchased Conway’s book On Numbers and Games around 1980, let alone the connections between games and complexity. The book has a lot of depth that might be useful to complexity theory. To quote Peter Sarnak, per this article by Conway’s biographer Siobhan Roberts on Conway’s meeting with Kurt Gödel:
The surreal numbers will be applied. It’s just a question of how and when.
Modular Programming
Most of us know that the conditional-jump instruction
if (x == 0) goto k
where k is the label of another instruction, creates a universal programming language when added to the usual programming primitives of assignment, sequencing, and simple arithmetic. Conway was a maven of the “modular-jump”:
if (x == 0 mod m) goto k.
In complexity theory we know that mod- gates having 0-1 inputs define the idea of
circuits, with
denoting problems solved by families of these circuits having fixed depth and polynomial size. If we don’t insist on fixed depth and unary inputs, we get modular programs. They are more complex than
circuits, but we can learn from what can be done concretely with them.
Conway created a particular form of modular programs in a language he called FRACTRAN. A program is just a list of positive fractions in lowest terms. The input is an integer
held in a separate register. Each fraction represents the code line
In other words, each iteration takes the first fraction such that
is an integer and updates
to
; if there is no such fraction then the program exits and outputs
.
For example, the following FRACTRAN program given in Wikipedia’s article implicitly computes integer division:
The notation is unary: The input has the form
and the ouput is
where
with remainder
. This already hints the fact that FRACTRAN is a universal programming language. Powers of primes serve as memory registers. The following program computes the Hamming weight
of the binary expansion of a natural number
encoded as
, returning the value
:
This might help bridge to our notions of . The Wikipedia article does a good job of de-mystifying the fractions in terms of their actions on the prime-power registers under the unary-style encoding. We wonder what happens when we try to work directly with binary encodings.
The Collatz Example
The famous “” problem of Lothar Collatz is a case in point. It iterates the function
The following FRACTRAN program given by Kenneth Monks iterates under the unary encoding
:
Note that since the last fraction is an integer the program runs forever. If so that the input is
, it would go
and thus cycle, unless we stop it. The powers of
that appear in its output give the desired sequence.
More natural to us, however, is the following modular program—which can use binary or any notation:
start: if (n == 1) { halt; }
if (n == 0 mod 2) { goto div; }
n = 3*n + 1;
div: n = n/2;
goto start;
One can generalize the Collatz problem to moduli . For each
we have a linear transformation
that always gives an integer value when
. We want to know about the orbits of numbers
under this iteration.
In fact, this is exactly what FRACTRAN does. Take to be the least common multiple of the denominators
in a FRACTRAN program
. Then for each
we can list the remainders
that are multiples of
and we get
, with
. The Turing-universality of FRACTRAN then proves a general theorem Conway stated in 1972:
Theorem 1 Generalized Collatz-type problems for moduli
are undecidable.
Several followup papers have proved stronger and more particular forms of the undecidability. The paper by Monks linked above leverages the unary encoding to show that having is essentially without loss of generality for universality; it is titled “
Minus the
.”
Having digested universality, it is natural to wonder about complexity. Can we use modular programming to achieve stronger connections between number theory and complexity classes—classes above the level of , say? One possible mode of connection is exemplified by this paper from STACS 1994, which both Dick and I attended. We wonder whether the kind of connection noted by Terry Tao in his tribute to Conway can also smooth the way to understanding
.
Open Problems
Conway posed many open problems himself. Here is a list of five for which he posted cash rewards in the manner of Paul Erdős. The fifth was recently solved. The fourth can be stated in one sentence:
If a set of points in the plane intersects every convex region of area 1, then must it have pairs of points at arbitrarily small distances?
Our condolences go out to his family and all who were enthralled by him in the mathematical world. We could talk endlessly about his impact on mathematics education—even about simple things like how to prove that is irrational—or try to tangle with his applications of the “Monster” group to modular forms, but those must be for another time. Also see Scott Aaronson’s tribute and its comments section for many more stories and items.
[some small word and format changes, added link to Scott and may add others as time allows]
Trackbacks
- Some Mathematical Gems from John Conway | Matt Baker's Math Blog
- To cheer you up in difficult times II: Mysterious matching news by Gal Beniamini, Naom Nisan, Vijay Vazirani and Thorben Tröbst! | Combinatorics and more
- Topping the Hat | Gödel's Lost Letter and P=NP
- One Day, Three Stories | Gödel's Lost Letter and P=NP


Some footnotes. One more personal story regarding Life is that once my Christmas my wish list included a hundred-plus wood chips cut square, which my mother went to great lengths to fulfill. I had worked out that coloring one side black for live cells, using the blank side for newborn cells, and standing dead cells on end for easy culling, would be quicker and more reliable than using the kinds of counters I had to hand. Indeed, a final pass of flipping blank to black before the next iteration would improve on Conway’s own swapping out white stones for black stones on a Go board. But I soon gained access to computers, including a TRS-80 at home, and both speed and reliability were beyond comparison. I must say, however, that computer versions lose a sense of intimacy I felt the first time using pencil and eraser.
Left on the cutting-room floor were discussion of the time overheads for the Life-to-TM and TM-to-Life simulations and more details on the Conway numbers. References for the former include this by Paul Rendell and an earlier paper by Jean-Philippe Rennard on simulating logic gates, which appeared in a book titled Collision-Based Computing. But I recall a more-specific investigation of the time overheads as being quadtratic, which is “somewhere in my office” (when am I going there again?) but I could not find online. Regarding the latter, the set equation looks strange in that this absorption usually pertains to multiplication/concatenation, not addition. This is why I chose the symbol
looks strange in that this absorption usually pertains to multiplication/concatenation, not addition. This is why I chose the symbol  to denote it. It occurred to me that if
to denote it. It occurred to me that if  on the left were replaced by “
on the left were replaced by “ ” and
” and  on the right by “
on the right by “ ” then the absorption under addition would look right. But one cannot use “infinity” cavalierly because
” then the absorption under addition would look right. But one cannot use “infinity” cavalierly because  is used with
is used with  and other infinite sets as
and other infinite sets as 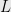 and/or
and/or 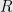 . Perhaps not the “void” but plus-and-minus versions of Cantor’s “Ultimate Aleph” superintend the creation. I chose angle brackets rather than the more-standard
. Perhaps not the “void” but plus-and-minus versions of Cantor’s “Ultimate Aleph” superintend the creation. I chose angle brackets rather than the more-standard  notation to avoid slurring e.g.
notation to avoid slurring e.g.  to
to  but maybe there is no harm in doing so.
but maybe there is no harm in doing so.
what a blow! curse this virus! conway was a huge inspiration to me, esp his number theoretic + computational work. he invented a “Fractran language” proof in the ~1970s that showed the undecidability of number theoretic propositions similar to Collatz, generalizing the basic structure. this work is rarely cited but think it is quite substantial esp in its relation to hilberts 10th problem which is quite celebrated.
another amazing proof of conway was proving Life is Turing complete. am not sure this proof was ever written down…? think the history of this needs to be better documented. it is built out of the idea of constructing a Turing machine out of Life-gadgets like gliders and glider guns where the glider positions determine 0/1 encoding. there was a web page by Rendell years ago that rendered a variant.
conway downplayed the signficance of the Life discovery but feel it was not so much false modesty but *unwarranted* modesty. its a discovery of 1st rate. the tendency of other mathematicians to downplay its significance is unwarranted. its a precursor to understanding concepts of complexity and emergence that marked 2nd 20th century math. in my pov its as much significance to math as the Lorenz attractor equations which are more celebrated.
was reading Wolfram recently who was clearly highly influenced by conway with cellular automata but does not (seem to) cite Conway much. would be very interested to understand better/ in more detail the interrelationship/ cross pollination between these two.
hope that someone writes a large, definitive popsci or higher level biography of Conway (ideally with lots of juicy math detail + citations), will be the 1st in line to buy that.
Thanks for this article… We could know so many things…
Thanks to Ken and Richard! Hope you are fine if I share this for others to know.
Nabendu, yes, absolutely fine…
As a regular reader – though not a regular understander – of your blog I just wanted to leave a link to the most lively article I found describing John CONWAY:
https://www.theguardian.com/science/2015/jul/23/john-horton-conway-the-most-charismatic-mathematician-in-the-world
Take care of yourselves.
Jack
Dear jack:
We appreciate your being a regular reader. We also thank you for the link. Conway was special.
Best and stay safe.
Dick
Not a comment so much as a couple of questions. Clearly Conway was familiar with quantum mechanics (QM) as the free will theorem demonstrated. I have always wondered if Conway was influenced by Dirac hole theory in his notion of the void? In addition, the left right notation has produces numbers in a manner analogous to to raising and lowering operators in the algebraic formulation of some problems in QM such as the harmonic oscillator as well as the some formulations in quantum field theory. Does any one know he discussed this in his popular lectures or his discussions of surreal numbers? I am sure that we will see surreal numbers in formulations in physics someday. “
JG, I don’t know enough to answer. You did pick up on some of my musings during the writing about whether there is any relation between the left-right notation and Dirac notation. I decided no—indeed, per my followup comment, I became less sure that “the void” is the correct implicit quantity—but decided to keep the Dirac brackets because I felt the standard braces cause other confusion about what is a set and what is not. (Ken writing this.)
thanks JEG
May your blog live long and prosper.