Proof of the Diagonal Lemma in Logic
Why is the proof so short yet so difficult?
|
Saeed Salehi is a logician at the University of Tabriz in Iran. Three years ago he gave a presentation at a Moscow workshop on proofs of the diagonal lemma.
Today I thought I would discuss the famous diagonal lemma.
The lemma is related to Georg Cantor’s famous diagonal argument yet is different. The logical version imposes requirements on when the argument applies, and requires that it be expressible within a formal system.
The lemma underpins Kurt Gödel’s famous 1931 proof that arithmetic is incomplete. However, Gödel did not state it as a lemma or proposition or theorem or anything else. Instead, he focused his attention on what we now call Gödel numbering. We consider this today as “obvious” but his paper’s title ended with “Part I”. And he had readied a “Part II” with over 100 pages of calculations should people question that his numbering scheme was expressible within the logic.
Only after his proof was understood did people realize that one part, perhaps the trickiest part, could be abstracted into a powerful lemma. The tricky part is not the Gödel numbering. People granted that it can be brought within the logic once they saw enough of Gödel’s evidence, and so we may write 
This is what we will try to motivate.
Tracing the Lemma
Rudolf Carnap is often credited with the first formal statement, in 1934, for instance by Eliott Mendelson in his famous textbook on logic. Carnap was a member of the Vienna Circle, which Gödel frequented, and Carnap is considered a giant among twentieth-century philosophers. He worked on sweeping grand problems of philosophy, including logical positivism and analysis of human language via syntax before semantics. Yet it strikes us with irony that his work on the lemma may be the best remembered.
Who did the lemma first? Let’s leave that for others and move on to the mystery of how to prove the lemma once it is stated. I must say the lemma is easy to state, easy to remember, and has a short proof. But I believe that the proof is not easy to remember or even follow.
Salehi’s presentation quotes others’ opinions about the proof:
|
So I am not alone, and I thought it might be useful to try and unravel its proof. This exercise helped me and maybe it will help you.
Here goes.
Stating the Lemma
Let 
Formally,
Lemma 1 Suppose that
is some formula in
. Then there is a sentence
so that
The beauty of this lemma is that it was used by Gödel and others to prove various powerful theorems. For example, the lemma quickly proves this result of Alfred Tarski:
Theorem 2 Suppose that
so that for all sentences
The proof is this. Assume there is such a formula 
This shows that
This is a contradiction. A short proof.
The Proof
The key is to define the function 
If 
and
Now we make two definitions:
Now we compute just using the definitions of 
We are done.
But …
Where did this proof come from? Suppose that you forgot the proof but remember the statement of the lemma. I claim that we can then reconstruct the proof.
First let’s ask: Where did the definition of the function
But left
But we want 
This essentially gives the definition of the function
But but …
Okay where did the definition of 
for some 
Okay how about the definition of
Taking an Exam
Another way to think about the diagonal lemma is imagine you are taking an exam in logic. The first question is:
Prove in
You read the question again and think: “I wish I had studied harder, I should have not have checked Facebook last night. And then went out and 
Here is what you do. You say let me define
for some 
But you think: I need a sentence 
It is after all the diagonal lemma. Hmmm does this work. Let’s see if this works. Wait as above I get that
Great this works. I think this is the proof. Wonderful. Got the first question.
Let’s look at the next exam question. Oh no
Open Problems
Does this help? Does this unravel the mystery of the proof? Or is it still magic?
[Fixed equation formatting]
Cool! I once reviewed a paper of Salehi.
I’ve always felt that von Neumann’s theory of self-reproducing machines sheds the most
light on the diagonal lemma. (See pp.64-66 of these notes, from this webpage.)
I’ve always felt that von Neumann’s theory of self-reproducing automatat sheds the most light on the diagonal lemma. (See pp.64-66 of the notes “Basics of First-Order Logic” on this webpage.)
First comment is moderated, then comments are automatic for an X time period—where we don’t know X. We also don’t know if deleting someone’s comments gets scored against X, so let us know if another comment doesn’t come thru right away.
Latex is not rendering from “Now we make two definitions:” to “that happens provided”
Thanks—fixed. We sometimes forget which LaTeX features are rendered.
What is the parenthetization of the Lemma? Is it
(PA ⊢ φ) ⇔ S(⌜φ⌝)
or is it
PA ⊢ (φ ⇔ S(⌜φ⌝) )
Dear Bruno:
We mean the latter. That is PA ⊢ (φ ⇔ S(⌜φ⌝) ). Sorry for the confusion.
Best and be safe
Dick
The diagonal lemma looks very similar to fixed point theorems in recursion theory.
Is there a formal or historical connection between the two ?
Yup, I second Pascal Koiran.
Isn’t this about the same than Kleene second recursion theorem?
Indeed (kevembuangga and Pascal), I had a thought to add my own 2cents by tying it to some old notes on motivating the fixed-point Recursion Theorem:
https://cse.buffalo.edu/~regan/cse596/CSE596pgthms.pdf
But Dick’s post was already long enough and I’ve never taken time to polish or finish these notes; the chess world has been keeping me insanely busy all month.
My issue with the Diagonal Argument is that it is a halting algorithm (discovered before the Theory of Computation), personally I think every algorithm capable of solving the Halting Problem is physically unrealizable (“Unreal”? It’s funny that that this turns the chosen terminology “Real Numbers” an oxymoron)… Just as traveling to the past would lead to logical paradoxes, algorithms that solve the halting problem seem to be in the same ballpark…
I am still waiting for some Logician out there to mix Ultrafinitism and Theory of Computation into a Foundation (UltraComputationism?) that simply discards the physically unrealizable. If you have only a countable sets then the Axiom of Choice becomes a trivial theorem… Modern Constructivism research might already have all the necessary pieces, but doesn’t seem much interested in Foundations?
This is much more intuitive to prove via the recursion theorem which itself can be motivated by the idea that an appropriate notion of computation allows a machine to read it’s own source code.
James Owings’ “Diagonalization and the recursion theorem” (https://projecteuclid.org/euclid.ndjfl/1093890812) views the recursion theorem (and the diagonal lemma, and various other related results) as a failed diagonalization. (In Soare’s “Turing Computability” some of that material can be found in Section 2.2.4 “A Diagonal Argument which Fails”.) That way of thinking about the diagonal lemma removes some of the magic. The connection to Cantor’s argument is so direct that one may be tempted to conjecture that this is how Goedel arrived at his insight.
Marcus
Reblogged this on Magazino.
I have a question… How do you compute the Gödel number
? Given any formula $S(x)$ I understand how to create a Gödel number: You simply have each symbol of the formula represent a different number, and use those numbers as powers of primes. For instance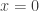 
might have a coding of 
where 
represent 
respectively and 
code the first, second, and third symbols of the formula.
The problem with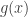
is that it contains a function 
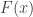for the input for the free variable in the formual 
. How is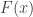 
represented in the Gödel coding? If 
what is 
and 
?
A very elementary beginner question: Say S(x) is the formula x = zero. There is only one numeral that can be substituted in for x to make S(x) provable, namely S(zero). However, no reasonable Godel numbering would have zero be the Godel number of a syntactically valid formula, much less a provable one. So, how do you find phi for this example? Is the claim of the lemma that phi and S(godelNumber(phi)) are both either provable or their syntactic negations are both provable? I.e., if the arrow symbol in the lemma was syntactic as opposed to meta-mathematical, then I suppose you could use a contraposition tautology as an axiom and deduce the formula not phi not S(godelNum(phi)). In that case, basically every formula that is provably false would suffice, because none of them would satisfy the particular S() in this example, and all would be provably false. The lemma would presumably pick one such example. I’m wondering if there is a “least” value the lemma generates, similar to least fixed points in denotational semantics, if there are multiple candidates for phi. BTW – thanks for this great posting!
Dear Greg Johnson:
Thanks for your kind interest. Let me think about this. You are right about 0 not the number of 0.
Best
Dick
One thought/speculation: The theorem does not assert the existence of a phi such that phi and S(phi) are both provable. It only asserts the existence of a phi such that the provability status of the formulas phi and S(phi) is the same. So, any provably false formula phi would do; S(phi) would also not be provable. An even crazier example would be S(x) == x < 0. There is no WFF phi at all whose Godel number would make S(n) provable, so any WFF that is provably false would suffice to satisfy the theorem in this case.
Regarding your open question: While I could follow and replicate your logic, the “aha” still eluded me, and left me feeling that there is more magic to be brought out into the open! Struggling with your elegant and thought-provoking article, something finally clicked, and I finally understood, came into direct contact with, and stood in awe of the genius of Kurt Godel.
My path to intuition was via lambda calculus. I translated your derivation in a somewhat rough and ready manner into the Y combinator:
Your F(x) can be thought to correspond to (x x), a well-formed lambda expression with one free variable.
g(w) then maps to S(F(w)), which by the above corresponds to S(w w).
We now wish to view g(w) as a function and apply it, so let us abstract:
g = lambda w.S(w w)
g(g) then becomes:
(lambda w.S(w w)) (lambda w.S(w w))
This is our candidate expression for phi. (And is, of course, the Y combinator applied to S.)
Now, let’s do one function application to the above expression for phi. (“beta reduction” in lambda calculus terms.)
Taking the body of the left-hand term and replacing instances of “w” with the right-hand term, we get:
S(lambda w.S(w w)) (lambda w.S(w w))
And this is precisely S(phi).
So, one might say that Kurt Godel effectively invented the Y combinator. In his proof, it seems that he started with something like S(F(x)): “for all p, not isProof(p, x, x)”. He then took the Godel number of this expression, and substituted it in for x. So, his “phi” was actually something like S(lambda w.S(w w)) (lambda w.S(w w)), which he then transformed via the equivalent in logic of beta reduction to S(S(lambda w.S(w w)) (lambda w.S(w w))). The new outer S is then interpreted to assert that its argument has no proof, but the WFF that therefore has no proof is exactly “phi”.