Highlights of FOCS Theory Day
A summary of a great day of talks before FOCS at Theory Day

Dick Karp was the leadoff speaker this Saturday at the FOCS Theory Day
in Atlanta. He was followed by Mihalis Yannakakis, Noga Alon, and Manny Blum. Sounds to me like a lineup for a baseball team that is in the World Series. I can almost hear an announcer saying:
Now batting cleanup, Mannnnny Blummmmm.
And the crowd goes wild.
Today I thought I would write a summary of what Dick and the others said Saturday. The talks were webcast, but perhaps not all of you watched them. In any event I will add some additional comments that I hope you enjoy.
All of these speakers always give great talks, and this day was no exception. I did notice that Karp and Blum both have titles that ask a question. Is this meaningful?
I cannot resist one story about Dick. Years ago he visited Atlanta to give the keynote at a conference. Rich DeMillo was the program chair, and he and I went out to the airport to pick Karp up. We planned to eat lunch, and then get Dick to the venue for his address. During the lunch we had a wonderful time chatting with Karp. Finally, at one point Dick said that he had a small issue that he was worried about. We of course asked what it was—we were prepared to help him in anyway possible.
Dick explained that he made his slides on the long airplane ride from SFO to Atlanta. In those days talks were made by writing on plastic transparencies with colored pens; my personal favorite were vis-a-vis markers. Dick said that he was concerned about the new type of pens that he had used. He did not use vis-a-vis, but he had used a new brand. We said that was fine. But he added that he was a bit concerned how well the slides would project, since they looked pretty pale. The pens apparently were not as good as old reliable vis-a-vis.
After lunch we jumped in Rich’s car, raced over to the conference hotel, and quickly found the room where Dick’s talk was going to be held. We immediately checked out the projector and more importantly Dick’s slides. He was right—the colors were extremely pale and the slides were nearly impossible to read. But it was way too late to redo them, since the talk was just about to start. Some of the audience were already entering the room.
We went forward—there was no other option. Rich gave a wonderful introduction of Karp, there was a long applause, and then Dick started his talk. He gave a great presentation. Whether the slides are perfect or not, Dick has a way of speaking and presenting his ideas that transcends everything else. Whether the red on a slide, for example, was pale or dark was unimportant. When Dick finished there was again a long applause. His talk was a huge success, but I believe he did throw the new pens away.
Let’s move on to discuss the talks, which were all quite different styles. Yet each was a masterpiece given by one of the leaders of the field.
What Makes an Algorithm Great?
Karp started by quoting me, twice. I was a bit embarrassed—and secretly pleased. The first quote was that “Algorithms are Tiny,” which I have discussed earlier. By the way the ideas in that discussion are joint with Lenore Blum.
- Karp then began to discuss great algorithms based on various
criteria. The first list was historical:- The Positional Number system of Alkarismi.
- The Chinese Remainder Theorem—which is really an algorithm.
- The Euclidean Algorithm.
- Gaussian Elimination.
Impossible to argue with any on his list. Without positional numbers, I believe, that one could make the case that almost no modern algorithm is possible. The Chinese Remainder Theorem is one of my favorites, and the other two are clearly great.
- Karp then talked about several algorithms that he said were based on great ideas.
They were,- Linear Programming
- Primality Testing
- Fast Matrix Product
- TSP
- Integer Factoring
The famous simplex method for LP is still one of the best ways to solve linear programs. Karp pointed out that the ellipsoid method was a great theoretic result, but the interior-point methods were the first to solve LP’s in a way which was both in polynomial-time and practical. Karp gave a nice survey of the work on the TSP: he pointed out that Nicos Christofides’ wonderful
-approximation algorithm for the metric TSP is still the best known. If you somehow do not know it check it out. It was discovered in 1976—that’s a lot of FOCS’s ago. Dick also pointed out that Volker Strassen’s famous fast matrix product algorithm was a surprise to the mathematical community.
- Karp is an expert in so many things, but perhaps his roots are in combinatorial optimization. So he went into some detail on the great algorithms from that area.
- Minimum Spanning Tree
- Shortest Path in Graphs
- For-Fulkerson Max-flow Algorithm
- Gale-Shapley Stable Marriage
- General Matching in Graphs
In 1965 Jack Edmonds’ paper titled “Paths, Trees, and Flowers” not only showed how to do matching for non- bipartite graphs, but also laid out an informal basis of what later became P, NP, and co-NP. An incredible achievement for that point in time.
- Karp next discussed randomized algorithms. I sometimes think we could not have a FOCS meeting if we disallowed the use of randomization.
- Primality Testing
- Volume of Convex Bodies
- Counting Matchings
- Min-Cut of Graphs
- String Matching
- Hashing
All of these algorithms are great, and Karp spent some details on the volume algorithm of Alan Frieze and Ravi Kannan. He said nothing about the beautiful string matching algorithm that is due to Michael Rabin and himself. He was modest, but I am under no constraint. Their matching algorithm is one of the examples of the immense power of randomness. Their algorithm is theoretically fast and is practical. Actually it is more than practical, it is I believe the algorithm of choice for most packages. A wonderful algorithm, that would make my personal top ten.
- Karp talked next about heuristic algorithms. These, he said, present an important challenge to theory. The central question, of course, is why do they work so well in practice?
- Local Search
- Shotgun Sequencing Algorithm
- Simulated Annealing
Dick stated that Myers’ great work on sequencing was critical to the effort that first sequenced the human genome at Celera—then a company in competition with the NIH funded labs. What is so neat about Myers’ algorithm is that it required him to understand the structure of the human genome. The genome is not random, has structure, and that structure makes what Gene did so difficult.
- Karp and complexity theory:
- NLOG is Closed Under Complement
- Undirected Connectivity is in DLOG
- Space is More Powerful Than Time
Karp agreed with my earlier discussion that even complexity theory is really all about algorithms. He selected the above as the some of the most outstanding ones. John Hopcroft, Wolfgang Paul, and Leslie Valiant proved that deterministic time
is in deterministic space
. Their proof relies on several algorithmic ideas: the block-respecting method and the pebbling game strategy.
- Karp only had time to list a number of great algorithms that show that theory can have impact on the “real-world.” All of the algorithms in his list have changed the world.
- Fast Fourier Transform
- RSA Encryption
- Miller-Rabin Primality Test
- Reed-Solomon Codes
- Lempel-Ziv Compression
- Page Rank of Google
- Consistent Hashing of Akamai
- Viterbi and Hidden Markov Models
- Smith-Waterman
- Spectral Low Rank Approximation Algorithms
- Binary Decision Diagrams
Without these algorithms the world would stop: no web search, no digital music or movies, no security,
and on and on.
- Karp finally gave a short list of algorithms from the area of information transfer.
- Digital Fountain Codes
- CDMA
- Compressive Sensing of Images
The first is a breakthrough method of Michael Luby that is a near optimal erasure code. In many situations information may be lost, rather than corrupted. Since it is lost the decoder knows that it is missing, which allows for a whole different type of error correcting code. These codes are extremely powerful: they are easy to encode and decode, and need relatively few extra bits of redundancy. Compressive Sensing is a relatively recent idea that is based on deep mathematics, yet is rapidly changing image compression. The creators are David Donoho, Emmanuel Candès, Justin Romberg, and Terence Tao—see this for many papers and articles from the area.
The talk was wonderful. Wonderful. In one hour we were carried from ancient times, past the dawn of modern computational complexity, then to the modern era, and the present—with a peek at the future. A masterful talk by the master. Later in the meeting Alon said that he could not imagine doing what Karp did. I completely agree.
Computational Aspects of Equilibria.
Yannakakis spoke about equilibria phenomena in game theory and economic theory. He started by saying that he had two hours worth of slides, but kindly finished nicely on time: close to the von Neumann Bound. John von Neumann once defined the perfect length of a talk as a micro-century, which works out to just about minutes.
- Yannakakis first explained how many systems can evolve over time to a stable state. He spoke at some length about the classic example of neural nets and a 1982 theorem due to John Hopfield that proves that they always converge to a local minimum. The argument is based on showing that a certain potential function decreases and eventually reaches a local minimum.
- Yannakakis then switched to a discussion that was mostly about various types of games. He discussed in detail the famous result of John Nash, proved in 1950, that any non-zero sum game always has at least one mixed equilibria point.
- Yannakakis’ key point was that Nash’s proof that mixed equilibria always exist was based on the famous Brouwer Fixed Point Theorem (BFPT). This theorem that is named after Luitzen Brouwer is also, as Mihalis said, used to prove that a whole host of other game/economic systems have a stable equilibrium point.
- Yannakakis then showed the power of modern complexity theory. Just because the BFPT is used to prove something does not rule out the possibility that there is a proof that avoids it. But, this is not the case. He introduced three complexity classes:
,
, and
. They capture respectively: general
-player games,
-player games, and finally games that have pure equilibria. A beautiful point is that he could use these classes to show that BFPT is equivalent to Nash’s famous theorem for multiple player games, and thus it is essential for the proof. The power of modern complexity should not be underestimated. Without the crisp notion of a “complexity class” I cannot see how any result like this could even be stated—let alone proved. Terrific.
- Yannakakis also pointed out that solutions to multiple player games may not be rational numbers, in general. This was, by the way, known to Nash back in 1950. The problem with this is that then there may be no way to write down the exact solution to the problem. This plays havoc with complexity theory. Mihalis gave the analogy to the sum of square root problem: Is the following true,
where the
are natural numbers and
is a rational number. It is a long standing open problem whether or not this can be solved in polynomial time. See this for a discussion that I had earlier on this topic.
- Yannakakis finally gave us the usual news about the complexity classes: not much is known about their power. Oh well. The following diagram summarizes all that is known about them: (an arrow denotes inclusion)

His talk summarized quite neatly the relationship between equilibria problems and certain complexity classes. I wish that Yannakakis had more time to give more details—perhaps another talk.
Disjoint Paths, Isoperimetric Problems, and Graph Eigenvalues.
Alon started by pointing out that his first FOCS paper was at the . At that meeting, in 1984, he spoke on eigenvalues and expanders—he said he seemed to be stuck. He then pulled out a small piece of paper and proceeded to read,
I would like to thank the many FOCS program committees for their hard work and effort—except for the FOCS program committees of 1989, 2003, and 2006.
Even one of the greatest theorists in the world gets papers rejected from FOCS. This got a big laugh, yet I think it actually raises a serious question about the role of conferences. I know that is being discussed both on-line and off, but let’s move on to the rest of his talk and leave that discussion for another time and place.
Noga really gave highlights of two problems:
- Alon first discussed a kind of routing game. He imagines that you have some fixed
node degree
expander graph. The game is this: you will be given a series of requests of the form:
where this means that you are to find a set of edge disjoint paths from
to
for each
. He proves that on a special type of expander that not only can this be done for
such that
but that it can be done on-line. That is there is an algorithm that selects the path from
to
without knowing the requests that will follow,
This seems amazing to me. See the paper joint with Michael Capalbo for full details on how this works.
- Alon then spoke on spines. Imagine
dimension space divided into unit cubes. You are to select a subset of each cube so that this “spine” does not allow any non-trivial path that moves from cube to cube. In a sense the spines are a kind of geometric separator. Since separators play a key role in many parts of theory, it may come as no surprise that spines also are very useful. A deep result of Guy Kindler, Ryan O’Donnell, Anup Rao, and Avi Wigderson shows that a spine can have surface area bounded by
where
is the dimension of the space. However, the shape of their spine is essentially not known; it cannot be seen. The discussion here may help understand more about spines and their applications. Noga’s main result is a new uniform proof that solves this and other spine problems.
- Alon also had a simple piece of advice for all of us. He pointed out that we all use search engines to try to find mathematics that can help us in our research The trouble is that it is impossible to type in mathematical formulas into search engines. His suggestion is: give all your lemmas meaningful names. This may allow people to find your work, and then reference it. He gave an example of one of his lemmas:
Lemma: (A simple discrete vertex isoperimetric inequality on the
Dirichlet boundary condition)
When I Googled this “name” the second hit was his paper—not too bad.
A wonderful talk, with light touches, and beautiful results; even though it contained many technical parts, I believe that most came away with the basic ideas that Noga wanted to get across.
Can (Theoretical Computer) Science Come to Grips With Consciousness?
Blum spoke about a life long quest, that started when he was six years old, to understand consciousness. Blum has a record of looking at old problems in new ways, of looking at new problems in his own way, of creating whole fields of study, and thus we should take his ideas on what is “consciousness” very seriously. Let’s call this the: What is consciousness problem. (WICP).
It is hard to really do justice to his wonderful talk, but I think there are a few high level points that I can get right:
- Blum states that now may be the first time that real progress can be made on the WICP. This is due to the confluence of two events. The ability of researchers to use FMRI machines to watch a person’s brain as they think is relatively recent development. Second, is the maturing of a powerful theory called the Global Workspace Theory, which was created by Bernie Baars. I will not explain the theory, since I do not understand it. But Blum says that it has a very computational flavor, which may mean that theory can make an important contribution to the WICP.
- Blum explained that when he was a graduate student he worked with some of the greats such as Warren McCulloch and Walter Pitts. They are famous for their notion of the McCulloch-Pitts neuron, which they proved could be the basis of a universal computing device. Today we study threshold functions and the complexity class
that are modern versions of their pioneering work.
- Blum pointed out a simple fact about the eye that I found fascinating: In the dark take a light source, and quickly move it around in front of you. You will see a path of light. This happens, Manny explained, because the eye responds only to motion. Then, keep the light source fixed and now move your head around. You will not see a path of light: you will see just a point of light. Somehow the eye and brain together can tell the difference between these two cases. Terrific.
- Blum then shifted into a more theory oriented part of his talk. He explained what he called templates. They are his way of modeling how we solve problems. His stated goal is quite ambitious; if we could understand WICP he thinks that we might be able to make robots/agents that learn. The template model is a kind of tree. For example, suppose that you are trying to prove a theorem. Then, the root of the tree would contain a “hint” or some high-level idea that gets you thinking in the right way about your theorem. Below that would be more precise yet still informal pieces of information. Eventually, the leaves of the tree would contain more formal pieces that make up the actual proof.
- Blum had a simple but great piece of advice to us all. If you are faced with a problem that you cannot solve, then modify the problem. Change it. Try another problem. He argued that this often may be interesting by itself, and sometimes may shed light on the original problem. Great advice.
- Blum ended with a pretty puzzle. Is there a irrational number
so that
for a rational
? The answer is yes, and he explained how his templates could guide you to the solution to his problem.
A wonderful talk, from one of the great visionaries of the field.
Open Problems
Before turning to some open problems I want to thank the following people for making Theory day such a great success: Dani Denton, Milena Mihail, Dan Spielman, and Robin Thomas. Thanks for all your hard work.
Robin pointed out that it was also ACO’s anniversary, and all of the talks should be online later this week.
Now some open problems that each speaker implicitly raised:
Trackbacks
- FOCS days 2 and 3 and 0. « Form and Formlessness
- Rumors and Playing Games « Gödel’s Lost Letter and P=NP
- Is There a Test for Consciousness? « Gödel’s Lost Letter and P=NP
- Routing Forever on an Expander Graph « Gödel’s Lost Letter and P=NP
- Quantum Algorithms A Different View—Again « Gödel’s Lost Letter and P=NP


Thanks for the post. One tiny comment, Karp seems to say about compressive sensing that it “…yet is rapidly changing image compression..” when in fact it might be a little more optimal to say “…yet is slowly changing image acquisition..”. Whille FOCS is theory oriented and its public is mildly interested in hardware implementations, here is a surely incomplete list of technologies using CS:
http://igorcarron.googlepages.com/compressedsensinghardware
Thanks for the post. I tried to get what each speaker said as accurate as I could.
Thanks also for the pointer.
This was a *great* post. I will comment upon Karp’s talk from an engineering point of view.
When talking to students, Valentine Telegdi used to quote (engineer-trained!) Paul Dirac as saying “A Golden Era occurs when ordinary people can make extraordinary contributions.”
Aside: I’ve never been able to find that exact Dirac quote in the literature (although some of Dirac’s writings come close; see appended BibTeX), and so I’ve come to believe that Dirac’s quote was possibly improved-upon by Telegdi himself.
The Dirac/Telegdi aphorism points to an aspect of Karp’s great algorithms that is truly wonderful, namely, that communities of ordinary folks can-and-do use these great algorithms to create extraordinary achievements (example: tabulating the human genome via shotgun reconstruction algorithms).
Now, let’s follow Blum’s advice, and turn this observation into a question. What *new* algorithms might we find in the 21st century, that have sufficient scope to create *new* Golden Eras?
After all, by the end of the century, we’re all going to sharing a planet that has ten billion people on it. Just try calculating the amount of ecology-sustaining land area available per-person … it’s a mighty small area … even if mountains, deserts, and tundra-land are included.
The 21st century’s urgent need for Golden-Era algorithms—and the job-creating enterprises that Golden-Era algorithms foster—then follows from a pigeon-hole argument: 99.99999% of the world’s population will *not* be among the world’s top one thousand computer scientists and complexity theorists! 🙂
That is why—from the Dirac/Telegdi point of view—creating new Golden-Era algorithms is one of the most urgent and challenging tasks of computer science and complexity theory.
—————
@inproceedings{Dirac:75, Author = {P. A. M. Dirac}, Booktitle = {Directions in Physics}, Editor = {H. Hora and J. R. Shepanski}, Publisher = {Wiley-Interscience, New York}, Title = {The Development of Quantum Mechanics}, Year = 1978,annotation={“[In the early days of quantum mechanics\ \ldots\ ] It was a good description to say that it was a game, a very interesting game one could play. Whenever one solved one of the little problems, one could write a paper about it. It was very easy in those days for any second-rate physicist to do first-rate work. There has not been such a glorious time since. It is very difficult now for a first-rate physicist to do second-rate work.”}}
“A beautiful point is that he could use these classes to show that BFPT is equivalent to Nash’s famous theorem for multiple player games, and thus it is essential for the proof. The power of modern complexity should not be underestimated. Without the crisp notion of a “complexity class” I cannot see how any result like this could even be stated—let alone proved.”
You yourself (paraphrasing Yannakakis) stated the result without using complexity classes: “BFPT is equivalent to Nash’s famous theorem for multiple player games.”
I did not see the talk nor do I know the result, but it seems to me that results like this get proved throughout mathematics all the time, without the notion of a complexity class or anything like it.
The most prominent example that comes to mind is that Zorn’s Lemma is equivalent to the Axiom of Choice.
(In fact, the whole (sub-sub-)field of Reverse Mathematics is about proving the relative strength of various mathematical statements and proof techniques. Reverse Math does have “theories” (such as WKL_0) that are akin to “complexity classes” in many ways, but I do not know how essential they are to getting results.)
Maybe I have misunderstood your (or Yannakakis’s?) point, but if so, please clarify :).
I agree with your point. Bu even reverse math depends on the structure of logical theory. I think complexity classes serve the same role for his work. It is not a huge point however.
Great Post Professor!
I was kind of looking for someone to do this post – and this is excellent. Thanks for that.
I really liked the way Professor Blum talked about Galileo’s work. I think i will mention it because its so beautiful.
We all know that Galileo demonstrated the falsity of the ground held by an age old notion of Aristotle’s – of heavier objects falling to ground quicker than the lighter ones.
To modern day high school students (like me, i guess) this statement does not require a rethought. We sort of take it for granted.
I mean, as Professor Blum pointed out, one must question what Galileo found fundamentally disturbing about Aristotle’s hypothesis.
As Professor Blum observed, it must have occurred to Galileo that dropping two 1-Kg weights, one held in his left hand and the other in his right, with his arms outstretched, from the same height simultaneously should take same time – this, I believe, is a pretty reasonable hypothesis. Then one can imagine Galileo bringing his hands together and repeating the experiment. Its again reasonable to believe that the two weights would again take the same time as the one “clocked” by the first experiment.
Finally, one could imagine bringing them even closer together and attaching a piece of thread between the two weights and again one could expect the two weights to clock the same time.
But one should look at what Galileo just dropped. It was a 2-Kg weight!
Really, this is amazing analysis by Professor Blum of the thought process Galileo went through.
I think, maybe we should take a little time out (if possible!) to analyze some scientific things of antiquity.
I personally believe Archimedes calculation of area of circle and volume of sphere deserve some study. After all, they did it without integral calculus which is what most of us, i guess, would invoke to prove these statements.
Again Great post Professor! Thanks
Great post, Dick. I was back home nursing a flu and this gave me a good sense of the day’s events. It is amazing how much text you can produce in a day, and with good grammar, style and readability.
Thanks for your kind comment. Get well soon.
Could you please share the proof that there is an irrational with rational
with rational  ? (I know the solution for a variant.)
? (I know the solution for a variant.)
I think his proof was pretty simple. Suppose that a to a is equal to 2. Then, not hard, he said, to show that a cannot be rational. It clearly is not an integer. So a=p/q properly. But then like proof that square of 2 is irrational it follows that a is irrational.
The last point is why is the some a with this property. I believe that he left that out, but a continuity argument shows that must exist.
I like this, but not sure it the simplest proof.
Thank you! Just to make sure I understand, I’ll reformulate:
Let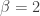 and suppose
and suppose  is rational, that is, suppose
is rational, that is, suppose  with
with  and
and  coprimes. Then
coprimes. Then  . Now let’s count factors of two on the left and right sides. (The fundamental theorem of arithmetic isn’t needed to prove that
. Now let’s count factors of two on the left and right sides. (The fundamental theorem of arithmetic isn’t needed to prove that 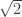 is irrational, but it is convenient.) Because there are some factors on the right side, there must be some on the left side. Say that
is irrational, but it is convenient.) Because there are some factors on the right side, there must be some on the left side. Say that  has
has  factors of
factors of  . (Then
. (Then  has none.) It follows that
has none.) It follows that  , which contradicts the assumption that
, which contradicts the assumption that  and
and  are co-primes.
are co-primes.
Perfect.
In fact, alpha^alpha can never be rational when alpha>0 is rational, unless alpha is an integer. Suppose alpha = p/q with p and q coprime, and beta = alpha^alpha is rational. Then (p/q)^p = beta^q. The exponents of all the prime factors of this number must be divisible by both p and q, and hence by pq. That means there is some rational number gamma such that beta = gamma^p and p/q = gamma^q. However, the last equation is impossible. If q>1, then gamma must have a nontrivial denominator since gamma^q is not an integer, and then gamma^q will have denominator at least 2^q, which is greater than q.
What is known about those “rumors”? 🙂
Coming this week.
Regarding the equivalence of Nash equilibrium and BFPT: Wikipedia claims that the existence of equilibrium in the Arrow-Debreu model can be used to prove the BTFT. http://en.wikipedia.org/wiki/General_equilibrium
This makes me wonder whether the result is entirely new.