Skip to content

The Depth Of The Möbius Function

February 23, 2011
tags: , , , ,
by


A striking connection between complexity theory and number theory

Peter Sarnak is an eminent number theorist, who has appointments at both Princeton University Mathematics Department and the Institute for Advanced Studies. He is also the editor of the Annals of Mathematics—one of the most prestigious journals in all of mathematics. And he is an expert on The Riemann Hypothesis.

Today I plan on discussing a recent post by Gil Kalai on a conjecture of Peter about the Möbius function.

Gil’s post, on his terrific blog, is based on a talk Peter gave on connections between number theory and complexity theory. You can skip the rest of this and just read Gil’s post: he stated the ideas probably clearer than I will. But I have my own take and perhaps you should read both. Gil thinks Peter’s conjecture looks attackable and I agree. If you solve it, please thank both of us. Alternatively, pick a random large integer {n}. If {n} is square-free, meaning no prime number squared divides {n}, then thank him; else thank me.

The Möbius Function

The conjecture is about the Möbius function which encodes information about the prime number structure of a natural number. The function is denoted by {\mu(n)} and takes on only values in the set {\{-1, 0, +1 \}}. It is defined by:

  1. Define {\mu(n) = 1}, if {n} is a square-free positive integer with an even number of prime factors.
  2. Define {\mu(n) = -1}, if {n} is a square-free positive integer with an odd number of prime factors.
  3. Define {\mu(n) = 0}, if {n} is not square-free.

Some examples: {\mu(1)=1}, {\mu(p)=-1}, and {\mu(p^2) = 0} for any prime {p}; and

\displaystyle \mu(30) = -1,

since {30 = 2 \cdot 3 \cdot 5}.

There are more-general kinds of Möbius functions that arise from partial orders. The above classic one actually arises from the partial order {x \prec y} if {x} divides {y}.

Why It Is Important?

The Möbius function clearly encodes the multiplicative structure of an integer, but that does not explain its great importance. In particular, why is the right choice to make {\mu(k)} zero for numbers {k} that have a repeated factor? There are many reasons why the current definition is the right one. Here are two basic ones:

{\bullet } Prime Number Theorem: This is the statement that

\displaystyle \pi(x) = \frac{x}{\ln x} + o(x/\ln x).

Here \pi(x) is the number of primes less than x . There are many equivalent versions of this key theorem, one is that it is equivalent to the statement:

\displaystyle \sum_{k \le x} \mu(k) = o(x).

{\bullet } Riemann Hypothesis: This is the statement that the nontrivial zeroes of the Riemann zeta function all have real part 1/2. It is the open problem in number theory and perhaps all of mathematics. Again there are many equivalent versions, one is that it is equivalent to the statement:

\displaystyle \sum_{k \le x} \mu(k) = O(x^{1/2+\epsilon}),

for any {\epsilon>0}. Note the gap between what is known and what is believed: the sum

\displaystyle \sum_{k \le x} \mu(k)

is known to be {o(x)}, but is believed to be much smaller—just above the square root of {x}.

One intuition about the Möbius function is that it behaves like a random variable: the values seem to be very erratic and unpredictable. This is the intuition, I believe, behind the belief that the sum

\displaystyle \sum_{k \le x} \mu(k)

grows much slower than {o(x)}. If the values were really random—they are not of course, but imagine that they were—then the sum would be closer to the square root of {x}. This would be a theorem if the values were truly random. Of course the values of {\mu(k)} are not random, since they satisfy many interesting properties. For example

\displaystyle \mu(a \cdot b) = \mu(a) \cdot \mu(b)

provided {a} and {b} are relatively prime. Another important property of the Möbius function is:

\displaystyle \sum_{k | x} \mu(k) = 0,

for {x>1}.

But in any event a good intuition is that {\mu(x)} does behave in a very erratic and unpredictable manner. This is reasoning, I believe, behind Peter’s conjecture.

The Conjecture

Peter’s Conjecture is the following: Suppose that {f(k)} is some function that is simple, then the sum

\displaystyle \sum_{k \le x} \mu(k) \cdot f(k) = o(x).

Gil suggests that we make “simple” precise by using complexity theory. Think of {k} as written in binary

\displaystyle k = 2^{n-1}k_{n-1} + \dots + 2k_1 + k_0.

Then insist that {f(k)} is defined by an boolean function

\displaystyle f^*(k_{n-1},\dots,k_1,k_0)

which is in {\mathsf{AC^0}}. What we mean is that for each {n} the value of {f(k)} on {n} bit binary numbers is computable by a constant depth and polynomial size circuit.

Let’s agree to call this the Sarnak-Kalai Conjecture (SKC). The conjecture is plausible, especially if one believes that the Möbius function is essentially a random one. The conjecture is deep, since it includes the Prime Number Theorem as a special case: just let {f(k)=1} for all {k}.

Even using a tiny power of {\mathsf{AC^0}} yields interesting results: For example, SKC implies that

\displaystyle \sum_{k \le x \text{ and } k \equiv 3 \bmod 32} \mu(k) = o(x).

This seems non-trivial to me.

SKC seems possible to solve, in the sense that there may be enough known about {\mathsf{AC^0}} to resolve it. But I do not see it as a trivial conjecture. It seems like a lovely conjecture that David Hilbert would like: recall he once said that

{\dots} I should still more demand for a mathematical problem if it is to be perfect; for what is clear and easily comprehended attracts, the complicated repels us.

Factoring

My favorite problem after {\mathsf{SAT}} and after graph isomorphism and after factoring—wait that is a loop. Well I like them all.

It is interesting that Peter does not believe that his conjecture could be

\displaystyle \sum_{k \le x} \mu(k)\cdot f(k) = o(x),

where {f(k)} is any polynomial time computable function. The reason is simple: he thinks that factoring is in polynomial time. It is good to know that I am not alone in this belief—pretty neat that a great number theorist believes factoring is in polynomial time too. If it is then {f(k)} could be {\mu(k)} and the sum would become

\displaystyle \sum_{k \le x} \mu(k)^2,

which is the number of square-free numbers below {x}. This is long known to be {\Omega(x)}: actually it is {\frac{6}{\pi^2}x + o(x)}. So if factoring is in polynomial time, then {f(k)} must be restricted to not be below polynomial time in complexity. This implies the following simple theorem:

Theorem: If the complexity class {\mathcal F} satisfies Peter’s Conjecture, then factoring is not in the class {\mathcal F}.

I find this connection quite interesting.

Open Problems

Solve the SKC. Or failing that at least show that some non-trivial subclass of functions satisfy the conjecture. I note that this conjecture seems related to work of Eric Allender, Michael Saks, and Igor Shparlinski that I have previously discussed here.

[fixed typos noted by first two commenters]

from → People, Proofs
42 Comments leave one →
  1. Farbod Shokrieh permalink
    February 23, 2011 9:23 am

    There are some typos in “the conjecture” section;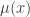 \mu(x) should be \mu(k).

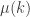    To me, another (main?) reason why the definition is the right one: Möbius function is the multiplicative inverse of the ”zeta function” of the incidence algebra of the poset (or more generally, the categorical algebra of the category).
    http://en.wikipedia.org/wiki/Incidence_algebra
    http://en.wikipedia.org/wiki/Categorical_algebra

    Reply
  2. Yury permalink
    February 23, 2011 9:51 am

    That’s very interesting connection between the number theory and complexity.

    Nitpicking: Probably, the statement of the conjecture should read “\sum_k \mu(k) f(k)” not “\sum_k \mu(x) f(k)”.

    Reply
    • KWRegan permalink*
      February 23, 2011 3:55 pm

      Owing to mod-queue + local timing issues, the identity of “the first two commenters” changed—but the typos were the same! 🙂

      Reply
  3. Andy Parrish permalink
    February 23, 2011 10:36 am

    Hi Dick,
    Thanks for sharing your thoughts on this conjecture. It’s certainly a fascinating one!

    Slight correction: the statement of Peter Sarnak’s conjecture and the consequence of SKC are both written as summation involving mu(x), which I believe should be mu(k).

    Reply
  4. Flavio Botelho permalink
    February 23, 2011 11:04 am

    There is a typo in “some examples”, u(p) should be -1

    Reply
  5. David permalink
    February 23, 2011 11:31 am

    Shouldn’t {\mu(p)=-1} because each prime {p} has just one prime factor, {p} itself.

    Reply
  6. Ross Snider permalink
    February 23, 2011 12:07 pm

    Two short things and a long thing:

    – You wrote that $\mu(p) = 1$ when it is clearly $-1$.
    – You did not motivate the Mobius function by deriving Mobius inversion! This is (IMHO) the best way to show that the Mobius function is “right.”

    The long thing. This is fantastic and may be what I decide to tackle if (*ahem*) _when_ I get accepted to graduate school. [Your own school, Professor Lipton, rejected me :-(]. Connections between Number Theory and Group Theory and complexity classes are precisely what I’d like to tackle (with connections to cryptography). Group Theory I think may be an interesting way to tackle the class separations, since group actions partition sets into orbits and because classes are just sets of sets of strings. Such an approach, I think, has a chance to avoid the known barriers to class separations, since group actions – if you choose the right groups – on a set aren’t likely to relativize.

    Reply
    • KWRegan permalink*
      February 23, 2011 12:47 pm

      Thanks to both you and Andy Parrish—fixed typos. Indeed, we could have mentioned Mo”bius inversion in-tandem with inclusion-exclusion, for which a good set of notes is here.

      Reply
      • rjlipton permalink*
        February 23, 2011 3:25 pm

        To All,

        Sorry for the typos. We try but it is hard to be perfect.

  7. Gil Kalai permalink
    February 23, 2011 1:39 pm

    We want to show that the Mobius function fools an AC0 circuit, so one recent result that comes to mind is Braverman’s result for polylog independence function. (And the earlier results by Bazzi and Rasborov.) The Mobius function is deterministic but maybe one can prove some properties that will allow to apply Braverman’s method. (Braverman’s method relies on the Linial-Mansour-Nisan theorem about the decay of Fourier coefficients of AC0 functions (nased on the switching lemme) plus an algebraic technique by Rasborov and Smolensky (and others). So can we replace something in the argument for r-wise independent functions by properties of Mobius functions. (This may well be nonsensical.)

    If we indeed need some strong “randomness” properties of the Mobius function there are some available methods that I know even less. I recall that a mathod by Vinogradov played a role for the results Peter described.

    Reply
  8. John Sidles permalink
    February 23, 2011 1:55 pm

    Often it is possible to discern engineering relevance in complexity-theoretic postulates … but (for me) not in this case. But it *is* a beautiful problem that I can enjoy mightily. Thank you, Gil and Dick and Ken!

    On TCS StackExchange, Hsien-Chih Chang has posted a well-considered question (unanswered at present) on the topic Efficiently computable functions as a counter-example to Peter’s conjecture, which explicitly credits both Gil’s Combinatorics and more and Gödel’s Lost Letter and P=NP as providing inspiration.

    This raises a meta-question with respect to the remarkable growth of MathOverflow and TCS StackExchange during 2010, and what some perceive to a concomitant decline in the blogosphere (noted by the Fortnow/GASARCH weblog, for example). Is the rise of the StackExchanges necessarily associated to a decline of the weblogs? A related question is, what social/academic norms might best govern the transfer of ideas back-and-forth between these media?

    Just to state my own view: I hope and expect that *all* kinds of media will prosper … and as to social/academic norms, in time they will sort themselves out, provided that people generally remember to act with common sense and good will.

    Reply
    • KWRegan permalink*
      February 23, 2011 3:58 pm

      Thanks, John: Often it goes the other way—Dick checks the “competition” even more than I, and that leads to an idea… Synergy not “junta”-ness is the goal.

      Reply
  9. luca permalink
    February 23, 2011 2:12 pm

    Green and Tao have proved a remarkable series of results on the pseudorandomness of the Mobius function.

    http://arxiv.org/abs/math/0606087
    http://arxiv.org/abs/0807.1736

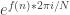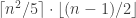    In the above papers, they show that the Mobius function “fools” bounded-step nilsequences, which are, roughly, expressions of the form e^{f(n)*2\pi i/N} where f() is a “constant-degree bracket polynomial”, that is an expression like \lceil n^2/5 \rceil \cdot \lfloor (n-1)/2\rfloor.

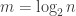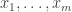    If you think of n as a string of m = \log_2 n bits x_1,\ldots,x_m , this is probably in the ballpark of fooling the sign of a constant-degree polynomial of the x_i. (Not that such a result is known or implied by the Green-Tao work.) AC0 has a characterization in terms of signs of logarithmic-degree polynomials, so there are definitely results in the right direction.

    Reply
    • rjlipton permalink*
      February 23, 2011 3:23 pm

      Luca

      Thanks for the pointer.

      Reply
    • Gil Kalai permalink
      February 26, 2011 12:07 pm

      Dear Luca, Are constant-degree-bracket-polynomials in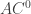 AC^0?

      Reply
  10. John Sidles permalink
    February 27, 2011 8:58 pm

    Just as an aside, the Wikipedia page on the Riemann ζ function gives a simple expression for 1/ζ(s) in terms of a sum over M&oum;bius functions; this expression helped me to appreciate why Riemann’s hypothesis follows from the heuristic assumption that the non-zero values of the M&oum;bius function are randomly distributed.

    Wikipedia gives a terrific heuristic justification for Goldbach’s conjecture … is there somewhere in the literature, a similar heuristic justification for the Riemann’s Hypothesis?

    In other words, might it the case that both Riemann’s and Goldbach’s conjectures are true, not only for the set of prime integers, but for most sets of randomly selected integers that are distributed in accord with the Prime Number Theorem?

    This intuition helps us (me anyway) to a partial appreciation of why both conjectures are so very hard to prove … the intuition is that central challenge is to prove, not theorems describing patterns in the primes, but (much harder!) theorems describing the lack of patterns in the distribution of primes.

    Reply
    • Gil Kalai permalink
      February 28, 2011 1:58 pm

      “In other words, might it the case that both Riemann’s and Goldbach’s conjectures are true, not only for the set of prime integers, but for most sets of randomly selected integers that are distributed in accord with the Prime Number Theorem?”

      This is a good question. When it come to Riemann’s conjecture I think that the answer is no in the following sense. If you replace the set of primes by a random dense subset of promes then the corresponding L-function do not exhibit the nice properties of Riemann zeta function that gives the RH. (Still the “new primes” will respect the PNT)

      Reply
      • John Sidles permalink
        February 28, 2011 2:32 pm

        Hi Gil! Well, just for fun … I actually *did* the (numerical) experiment … and your expectation is entirely correct! 🙂

        That is, if we randomly permute the first 10000 values of the Möbius function, then use the resulting pseudo-Möbius values to numerically compute a pseud0-ζ function … the resulting pseudo-ζ zeros show none of the special properties (AFIACT) of the zeros of the Riemann ζ function.

        In Mathematica this numerical experiment is readily coded … hopefully printing (in Mathematica) the following ASCII string will output a nice-looking expression.

        “\<
        <{{0,50},{0,2}}]
        \>”//Print;

      • John Sidles permalink
        February 28, 2011 2:34 pm

        Ooops … oh, well (as Dick says) … anyway, it’s easy to code … I will pathetically try once more … 🙂


        "\<
        <{{0,50},{0,2}}]
        \>"//Print;

  11. Gil Kalai permalink
    March 1, 2011 7:24 am

    It also looks to me that the conjecture that the Mobius function does not correlate with any function in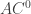 AC^0 is perhaps tracktable, related to recent results from number theory and from TCS and may require genuine connection between number theory and computational complexity. A small generalization that may also be tracktable is to consider 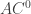AC^0 circuits with some additional random input variables and to conjecture that the relation from the post 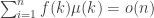\sum_{i=1}^n f(k)\mu(k)=o(n) holds with probability tending to 1.

    It is also interesting to think about questions regarding the complexity class P. Peter Sarnak challenged the audience to find a function $f$ which is computable in polynomial time with bounded-from-zero correlation with the Mobius function. The hope was that this will be considerably easier compared to actually computing the Mobius function. An attractive direction in the opposite direction would be to show that if you can have such a function f you can find an efficient way to “boost” the correlation with the Mobius function from a small constant to 1-o(1) or even further.

    Here is a challenge which is much much much weaker than what Peter suggested. so much so that maybe it is not hopeless: (There are 4 variants described by the square brackets) You can choose positive reals C and \epsilon as you wish.

    Problem: Find a [randomized] polynomial time algorithm to describe a function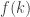 f(k) such that [for infinitely many values of n]

    \sum_{i=1}^n f(k)\mu (k) \ge C n^{1/2+\epsilon}.

    (This task is so much easier compared to Peter’s in that it being impossible implies both that factoring is not in P and the RH. Maybe it is possible then.)

    A related problem is:

    Problem: Find a [randomized] polynomial time algorithm to describe a function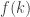 f(k) such that

    \sum_{i=1}^n f(k)\mu (k) \le C n^{1/2-\epsilon}.

    Reply
    • Gil Kalai permalink
      March 1, 2011 4:42 pm

      I think the first of my problems is silly: take f to be 1 for composite numbers and -1 for prime numbers. (Primality is in P.) The correlation with the Mobius function run away to n/logn. I dont know about the second problem.

      Reply
  12. Gil Kalai permalink
    March 6, 2011 4:00 am

    Dear Dick and all, I have posted two questions on Mathoverflow related to the conjecture. The first
    http://mathoverflow.net/questions/57230/discrete-fourier-transform-of-the-mobius-function
    is about the discrete Fourier coefficients of the Mobius function and the second
    http://mathoverflow.net/questions/57543/walsh-fourier-transform-of-mobius-functions
    is about Walsh-Fourier coefficients of the Mobius function. The second question
    has a direct baring on our question.

    Based on the answers to the first question, I am somehow more optimistic that the conjecture can be derived from GRH. I am less optimistic about an unconditional proof but there is slightly more hope for formulas (depth 2 circuits).

    The paper COMPLEXITY OF SOME ARITHMETIC PROBLEMS FOR BINARY POLYNOMIALS by Eric Allender, Anna Bernasconi, Carsten Damm, Joachim von zur Gathen, Michael Saks, and Igor Shparlinski and various papers by some of the authors contains relevant information. (Maybe even enough information to settle our problem, but I am not sure about it..)

    Reply
    • Gil Kalai permalink
      March 16, 2011 3:08 pm

      Update: Ben Green have posted an answer to my Mathoverflow question indicating an affarmative solution for the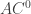 AC^0 Prime Number Conjecture (a.k.a. The Sarnak-Kalai Conjecture). The proof is based on combining the Linial-Mansour-Nisan theorem with Results and techniques by Glyn Harman and Imre Kátai, (From the paper Primes with preassigned digits. II. Acta Arith. 133 (2008), 171–184.)
      Ben have written some rough notes on this here:
      http://www.dpmms.cam.ac.uk/~bjg23/papers/primes-boolean.pdf
      The notes assumes GRH and it seems some work is needed to prove it unconditionally and Ben said he will explain how this is done in due course. This is a very nice result. Ben is also optimistic that showing that all Walsh-Fourier functions are orthogonal to Mobius is within reach by combining the above result with results by Mauduit-Rivat.

      Of course, the next logical state is the ACC[2]-Prime number conjecture.

      Reply
      • Gil Kalai permalink
        March 26, 2011 2:46 pm

        The conjecture have been proved by Ben Green. The link above have now transformed from being a rough 2-page notes to being a fully detailed 10 pages paper. (The proof does not assume GRH.)

  13. Mats Granvik permalink
    March 16, 2011 6:42 am

    Can anything be said about the Mobius function based on its generating function:

    \sum \limits_{n=1}^{\infty} \mu(n)x^n = x - \sum \limits_{a=2}^{\infty} x^{a} + \sum \limits_{b=2}^{\infty} \sum \limits_{a=2}^{\infty} x^{ab} - \sum \limits_{c=2}^{\infty} \sum \limits_{b=2}^{\infty} \sum \limits_{a=2}^{\infty} x^{abc} + \sum \limits_{d=2}^{\infty} \sum \limits_{c=2}^{\infty} \sum \limits_{b=2}^{\infty} \sum \limits_{a=2}^{\infty} x^{abcd} + ...

    Reply
    • Mats Granvik permalink
      March 16, 2011 6:55 am

      I had a typo in the latex code. The last sign before the dots should have been minus.
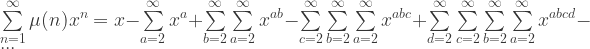
      \sum \limits_{n=1}^{\infty} \mu(n)x^n = x - \sum \limits_{a=2}^{\infty} x^{a} + \sum \limits_{b=2}^{\infty} \sum \limits_{a=2}^{\infty} x^{ab} - \sum \limits_{c=2}^{\infty} \sum \limits_{b=2}^{\infty} \sum \limits_{a=2}^{\infty} x^{abc} + \sum \limits_{d=2}^{\infty} \sum \limits_{c=2}^{\infty} \sum \limits_{b=2}^{\infty} \sum \limits_{a=2}^{\infty} x^{abcd} - ...

      Reply
  14. Farbod Shokrieh permalink
    March 27, 2011 8:45 pm

    Ben Green just put a paper on arXiv about this…
    http://arxiv.org/abs/1103.4991

    Reply
  15. Mats Granvik permalink
    June 22, 2012 5:12 am

    http://mobiusfunction.wordpress.com/2012/02/29/mobius-function-approximation-from-riemann-zeta-zeros/

    Reply
  16. Sunkhirous permalink
    August 7, 2012 8:13 pm

    I wonder what gave him the hint to come up with the conjecture !!!

    Reply
    • Craig permalink
      August 8, 2012 11:46 am

      My guess is he probably thought of the following: The Riemann Hypothesis is equivalent to the assertion that the Mertens function M(n)=o(n^{1/2+eps}), for each eps>0. If computing M(n) is hard, then proving that M(n))=o(n^{1/2+eps}) must be either very hard or impossible. This would explain why nobody has proven the RH.

      Reply
  17. Mats Granvik permalink
    March 28, 2014 9:12 am

    Möbius function from an arbitrary number sequence:
    http://math.stackexchange.com/questions/268159/mobius-function-from-random-number-sequence

    Reply

Trackbacks

  1. The Collatz Conjecture : Unsolved but Useless | Gaurav Happy Tiwari
  2. The AC0 Prime Number Conjecture | Combinatorics and more
  3. The Bourne Factor « Gödel’s Lost Letter and P=NP
  4. Connect the Stars « Gödel’s Lost Letter and P=NP
  5. July Fourth Sale Of Ideas « Gödel’s Lost Letter and P=NP
  6. Why We Lose Sleep Some Nights « Gödel’s Lost Letter and P=NP
  7. What Would Be Left, If…? « Gödel’s Lost Letter and P=NP
  8. Win Five Hundred Or A Million Dollars, By Recursion? | Gödel's Lost Letter and P=NP
  9. How can the Möbius function be applied to a series? - MathHub
  10. Preview of the Atiyah Talk | Gödel's Lost Letter and P=NP
  11. Watching Over the Zeroes | Gödel's Lost Letter and P=NP

Leave a Reply

Discover more from Gödel's Lost Letter and P=NP

Subscribe now to keep reading and get access to the full archive.

Continue reading