Perpetual Motion of The 21st Century?

January 30, 2012

by rjlipton

Are quantum errors incorrigible? Discussion between Gil Kalai and Aram Harrow

Gil Kalai and Aram Harrow are world experts on mathematical frameworks for quantum computation. They hold opposing opinions on whether or not quantum computers are possible.

Today and in at least one succeeding post, Gil and Aram will discuss the possibility of building large-scale quantum computers.

Quantum computers provide a 21st Century field for the kind of debate first led by Albert Einstein about the reach of quantum theory. One thought experiment by which Einstein tried to contravene the Uncertainty Principle can be described as having asserted that quantum theory implies the creation of perpetual motion machines, which are impossible machines. In a later attempt, after initial puzzlement, Niels Bohr pointed out that Einstein himself had neglected to correct for gravity’s effect on time in general relativity.

Perpetual motion machines were the dream of many inventors over the centuries—and why not? Having a machine that could create useful work but consume no fuel would change the world. Alas advances in our understanding of physics have ruled them out: there is indeed no free lunch. The designs at right look like birds-of-a-feather, but the rightmost was designed in 1960 by Hermann Bondi to illustrate Bohr’s correction above.

The guest discussions here between Gil Kalai and Aram Harrow address the fundamental question:

Are quantum computers feasible? Or are their underlying models defeated by some fundamental physical laws?

Those like Royal Society co-founder John Wilkins who in 1670 wrote of perpetual motion machines did not know of the second law of thermodynamics. We, Dick and Ken, would like to think that if blogs like GLL were around centuries ago there might have been a more penetrating discussion than even the Royal Society could foster. We are here now, and we are very honored that Gil and Aram wish to use GLL as a location to discuss this interesting, important, and wonderful question. We believe in the win-win that either we will have wonderful quantum computers, or we will learn some new laws of nature, particularly about information.

For a roadmap, Gil and Aram will alternate thesis-response in these posts, talking about quantum error-correction and fault tolerance. However, we also invite you, the reader, to take part in the debate sparked by Gil’s paper, “How quantum computers fail: Quantum codes, correlations in physical systems, and noise accumulation.”Perhaps they and we will react to comments. We thank them greatly, and have worked to make the issues even more accessible.

Guest Post: Gil Kalai

The discovery by Peter Shor of the famous quantum algorithm for fast integer factoring gave a strong reason to be skeptical about quantum computers (QC’s), along with an even stronger reason for wanting to build them. Shor is also the pioneer of quantum error-correction and quantum fault-tolerance, which give good reasons to believe that QC’s can be built. Other researchers have focused on this very issue, and the physics community is filled with work on many approaches to building practical QC’s.

In my (Gil’s) part of the world, Michael Ben-Or is a world leader in theoretical computer science with major contributions in cryptography, complexity, randomization, distributed algorithms, and quantum computation. Among the famous notions associated with Michael’s work before he turned quantum are non-cryptographic fault-tolerance, multi-prover interactive proofs, and algebraic decision trees. Dorit Aharonov is one of the great quantum computation researchers in the world and she has studied, among other things, fault tolerance, adiabatic computation, lattice problems, computation of Jones polynomials, and quantum Hamiltonian complexity.

Aharonov and Ben-Or proved in the mid-1990s (along with other groups) the threshold theorem which allows fault tolerant quantum computation (FTQC) at least in theory. The following photo shows them on the road in Jerusalem in 2005 with me at left, and on the right Robert Alicki, a famous quantum physicist from Gdansk, Poland, known for work on quantum dynamical systems.

Alicki is perhaps the only physicist engaged in long-term research skeptical towards quantum computers and error-correction. Over the years he has produced several papers and critiques under this program, coming from several different directions: some based on thermodynamics, others based on various issues in modeling noisy quantum evolutions.

Conjectures on noisy QC’s and error-correction

I suppose readers here are familiar with the basic concepts of quantum computers: qubits, basis states as members of ${\{0,1\}^n}$ , superposition, entanglement, interference. My comments in the first round of discussions are based on several (related) papers of mine, mainly the one linked above (alternate link). A more technical paper is “When noise accumulates.” Here are slides from a related lecture at Caltech’s Institute for Quantum Information, and an earlier, more-detailed, survey. The feasibility of building quantum computers that can out-perform digital computers is one of the most fascinating and clear-cut scientific problems of our time. The main concern is that quantum systems are inherently noisy. Roughly what this means for QC’s is that the internal states of quantum registers may vary unpredictably outside the range that allows the algorithm to continue.

First consider a single classical bit ${b}$ with some probability ${p < 1/2}$ of being flipped when read. For any ${\delta > 0}$ we can improve the odds of correct reading above ${1-\delta}$ by making and sending enough separate copies ${b,b,b,\ldots,b}$ . In case of any flips the reader will take the majority value, and this works provided the error events on the different bits are independent. For strings of bits there are error correcting codes that achieve the same guarantee more efficiently than making copies, and that can also cope with limited kinds of correlated errors such as “burst noise” which affects consecutive bits.

For quantum systems there are special obstacles, such as the inability to make exact copies of quantum states in general. Nevertheless, much of the theory of error-correction has been carried over, and the famous threshold theorem shows that fault-tolerant quantum computation (FTQC) is possible if certain conditions are met. The most-emphasized condition sets a threshold for the absolute rate of error, one still orders of magnitude more stringent than what current technology achieves but approachable. One issue raised here, however, is whether the errors have sufficient independence for these schemes to work or correlations limited to what they can handle. I will now go on to describe my conjectures regarding how noisy quantum computers really behave.

Conjecture 1 (No quantum error-correction): In every implementation of quantum error-correcting codes with one encoded qubit, the probability of not getting the intended qubit is at least some ${\delta > 0}$ , independently of the number of qubits used for encoding.

Conjecture 1 does not obstruct classical error correction as described above. The rationale behind Conjecture 1 is that when you implement the decoding from a single qubit to ${n}$ qubits ${f(x) \rightarrow (x_1,x_2,\dots,x_n)}$ , a noise in the input ${x}$ amounts to having a mixture with undesired code words. The conjecture asserts that, for a realistic implementation of quantum error-correction, there is no way around it. Conjecture 1 reflects a strong conjectural interpretation of the principle that quantum systems are inherently noisy:

Conjecture 2 (The strong principle of noise): Quantum systems are inherently noisy with respect to every Hilbert space used in their description.

The next two conjectures concern noise among entangled qubits—proposed mathematical formulations for them are in the paper.

Conjecture 3: A noisy quantum computer is subject to noise in which error events for two substantially entangled qubits have a substantial positive correlation.

Conjecture 4: In any quantum computer at a highly entangled state there will be a strong effect of error synchronization.

Standard circuit or machine models of QC’s divide the computation into discrete cycles, between which one can identify “fresh noise” apart from the accumulated effect of previous noise. The threshold theorem does entail that (when the noise rate is under the threshold) for FTQC to fail, these conjectures must hold for the fresh noise. A QC model in which fresh noise shows these effects differs sharply from the assumptions underlying standard models. I proved that a strong form of Conjecture 3, where “entanglement” is replaced by a certain notion of “emergent entanglement,” implies Conjecture 4.

Conjectured Limit on Entanglement

The papers argue a few other conjectures regarding how noisy quantum computers behave. One describes noisy quantum evolutions that do not enact quantum fault tolerance, which we skip here. The most quantitative one is called Conjecture C in the technical paper on noise, C for censorship because it concerns what types of (highly entangled) quantum states cannot be reached at all by such noisy QC’s.

Consider a QC with a set ${A}$ of ${n}$ qubits. Given a subset ${B}$ of ${m}$ qubits, consider the convex hull ${F}$ of all states that for some ${k}$ factor into a tensor product of a state on some ${k}$ of the qubits and a state on the other ${m-k}$ qubits. For a state ${\tau}$ on ${B}$ , define ${ENT(\tau,B)}$ as the trace distance between ${\tau}$ and ${F}$ . For a state ${\rho}$ of all the ${n}$ qubits, define ${\widetilde{ENT}(\rho)=\sum \{ENT(\rho|_B): B\subset A\}}$ .

Conjecture C: There is a polynomial ${P(n)}$ (perhaps even a quadratic polynomial) such that for any QC on ${n}$ qubits, which describes a state ${\rho}$ (which need not be pure), ${\widetilde{ENT}(\rho)\le P(n)}$ .

Here QC can be regarded as a quantum circuit given initial state ${|0>^{\otimes n}}$ .

Interpreting and Testing the Conjectures

The strong interpretation is that the conjectures hold globally, for any quantum dynamical system on which a QC can be based. The medium interpretation says they hold for processes currently observed in nature, but human artifice can create systems in which they are false, thus allowing computationally superior QC’s to be built via FTQC. The weak interpretation is that they only make a sharp distinction between two kinds of QC models, one supporting FTQC and the other not, and that the former kind can be built artificially and also does represent some quantum processes that occur naturally.

I tend to believe in the strong interpretation, namely, that the conjectures are always true. The weaker interpretations can be used to discuss (as we do below) specific proposals for implementing quantum computation. There are quite a few suggestions on how to build quantum computers based on qubits and gates, and also some suggestions based on computationally equivalent but physically quite different methods.

Nevertheless, I do not expect a common physical reason why my conjectures should apply for each proposed realization of a QC. Hence the conjectures should be examined, either based on detailed modeling, or based on experimentation, on a case-by-case basis. Note that they are not about some mysterious breakdown that occurs when you try to scale quantum computers to a large number of qubits. Conjecture 3 is about the two-qubit behavior of a quantum computer with any number of qubits, and it can be checked (as can the other conjectures) on quantum computers with a rather small number of qubits.

One prominent proposal under which the conjectures can be tested is measurement-based QC employing cluster states. Cluster states can be regarded as code words in a certain quantum error-correcting code. Once you prepare such states, universal quantum-computing can be achieved by a certain measurement of the state. Conjecture 1 asserts that noisy quantum states created in the laboratory will involve a mixture of the intended state with other cluster states.

Question 1: Will such noisy cluster states still support universal quantum-computing?

A second proposal is topological quantum computing. Non-abelian anyons that can support universal quantum-computing can also be regarded as codewords in a certain quantum error-correcting code. Similar to before, the conjecture asserts that when we create such states in the laboratory (in a process that does not apply quantum fault-tolerance) we achieve a mixture of intended codewords with unintended codewords.

Question 2: Will such noisy anyons be useful for universal quantum-computing?

For these two proposals the special physical gadgets are supposed to be constructible by “ordinary” experimental quantum physics that does not involve quantum fault-tolerance, so they are an especially appealing testbed for my conjectures where all three interpretations can apply.

Why I Believe My Conjectures

Let me explain why I think that my conjectures are correct—also mindful of this nice post by Shmuel Weinberger on what “a conjecture” means for a mathematician. I regard it as implausible (see below) that universal quantum computers are realistic, and I think that the issue of noise is indeed the main issue. The strong principle of noise underlying Conjecture 1 strikes me as the right way to approach noise in quantum systems to begin with. The two-qubit conjecture proposes the simplest dividing line that I can think of between noise that allows fault tolerance and noise that does not. The conjecture regarding error-synchronization also captures, in my opinion, a very basic obstacle to quantum fault-tolerance. There is an argument from first principles that since error-correction is possible classically and Nature is really quantum, then error-correction must be possible quantumly. But it strikes me as conflating the settings after-the-fact. In any case, my conjectures allow classical error-correction and fault tolerance. And, finally, as far as I can see, my conjectures on the behavior of noise do not violate any principle of quantum mechanics.

As an aside, let me briefly say why I tend to regard universal quantum computers as unrealistic. An explanation for why universal quantum computers are unrealistic may require some change in physics theory of quantum decoherence. On the other hand, universal quantum computers will be physical devices that are able to simulate arbitrary quantum evolutions, where the word “simulate” is understood in the strong sense that the computer will actually create an identical quantum state to the state created by the evolution it simulates, and the word “arbitrary” is understood in the strong sense that it applies to every quantum evolution we can imagine as long as it obeys the rules of quantum mechanics. As such, quantum computers propose a major change in physical reality.

Aram Harrow: A Short Response

Although Peter Shor has already been featured on this blog for his famous factoring algorithm, I want to mention an arguably deeper contribution of his to quantum information. After demonstrating that ${n}$ -bit numbers could be factored in ${O(n^2)}$ time, Shor pointed out that this was possible even with noisy gates, as long as each gate’s noise was ${o(1/n^2)}$ (This observation is not totally obvious, and rests on the fact that quantum computers, unlike analog computers, cannot magnify small errors in their amplitudes.) Shor made this point to argue that factoring can be achieved with resources that are genuinely only polynomial, even when counting time, number of processors, energy and precision. When proposing new models of computation, it’s important to not to fall into the trap of analog computing, where seemingly innocuous assumptions dramatically change the power of the model.

While requiring noise to scale as ${1/\mathsf{poly}(n)}$ might be theoretically reasonable, it’s not very encouraging if we hope to ever build a large-scale quantum computer. In the mid 1990’s, many disbelieved that quantum decoherence could ever be significantly reduced. Shor (and others) responded to this by developing the theory of quantum error correcting codes (QECC), which protect data in a manner analogous to classical codes. This requires overcoming several difficulties, such as the no-cloning theorem (which prevents redundant encodings), the fact that measurements cause disturbance, and the continuous range of possible errors.

Later, Shor (and Aharonov and Ben-Or, and others) extended QECCs to protect dynamic computations, so that fault-tolerant quantum computing (FTQC) could be achieved in the presence of a sufficiently low, but constant, rate of errors. To be sure, this makes assumptions such as independence that Gil is questioning.

QECC and FTQC are more than an answer to a technical objection; together they describe a potentially new phase of matter. In my opinion, they represent the deepest discovery in quantum mechanics since Bell’s Theorem. And we have in part the criticism of the quantum computing skeptics to thank for these breakthroughs! I hope the conversation between Gil’s skepticism and the optimism of people like me will also lead to useful results.

In a later post, I’ll respond in detail about why I believe that the emperor is fully dressed, and large-scale FTQC is possible, not only in theory, but realistically in the not-too-distant future. But by way of preview, I’ll outline my arguments briefly here.

Response Road Map

Any argument that FTQC is impossible must also deal with the fact that classical computing is evidently possible. Just as we know that any ${\mathsf{P}}$ vs ${\mathsf{NP}}$ proof must avoid working relative to every oracle, we can argue that any proof of quantum computing’s impossibility must somehow distinguish quantum computers from classical computers. This rules out most models of maliciously correlated errors.

The key assumption of FTQC is (approximately) independent errors. Conversely, Gil’s skepticism is based on error models that may have low single-qubit error rates, but are highly correlated even across large distances. While this possibility can’t be definitively ruled out until we build a working large-scale quantum computer, I’ll give both theoretical and experimental evidence that such error models don’t occur in nature.
Current routes to building quantum computers, such as ion traps and superconductors, nevertheless suffer from correlated errors. I think these correlations aren’t too bad, but they definitely exist. However, I’ll propose a thought-experiment implementation of a quantum computer, which is not meant to be practical, but where correlated errors are highly implausible.

Open Problems

What are your thoughts on this matter? Please try to be as clear as possible, and if you refer to specific issues raised here this will be especially good. Also, solve Questions 1 and 2.

[fixed intro’s conflation of two Einstein-Bohr interchanges]

236 Comments leave one →

Cristopher Moore permalink

January 30, 2012 12:12 pm

I have to channel Scott Aaronson here, and say that the skeptics of quantum computing are really skeptics of quantum mechanics. In particular, the claim that there is a fundamental limit on entanglement implies that quantum mechanics, as we currently believe it, is false: for instance, that there is some automatic process that decoheres the wave function at large scales, due to some nonlinearity in Schrodinger’s equations.

The problem is that experimental searches for such nonlinearities have shown that they are either zero, or incredibly small. Hence the truism that the quantum mechanics is, quantitatively, the best-verified physical theory. And if you believe that QM is correct, then states of arbitrarily large entanglement can be created.

The question about correlated noise is less clear to me, but as Aram hints, a skeptic might find themselves in the position of postulating correlations over very large distances. What would be the physical mechanism for this?

I am also a little confused by Gil’s motivation for his conjectures. It’s reasonable to take as a physical postulate (as Scott does) that NP-complete problems can’t be solved by a physical device in polynomial time (and I might add polynomial energy, since in physics you can often trade energy for time). But I don’t see why the factoring problem deserves this status.

Thus I would be much more interested in engaging with the skeptics if, rather than computer science-style conjectures that certain algorithms are impossible, they made conjectures about the underlying physics, proposing an alternative to QM that would explain the phenomena we have observed while making large-scale quantum computing impossible. I think it’s fair to say that, except for some rather convoluted and poorly-motivated proposals like Penrose’s that nothing with much mass can be in a quantum state, there is no such alternative theory currently known to us.

Gil also says “Universal quantum computers will be physical devices that are able to simulate arbitrary quantum evolutions, where the word “simulate” is understood in the strong sense that the computer will actually create an identical quantum state to the state created by the evolution it simulates… As such, quantum computers propose a major change in physical reality.” I don’t think this is correct. Quantum computers will simulate quantum systems in exactly the same way that classical computers simulate classical ones, namely subject to some encoding and with some amount of error.

The weak version of Gil’s conjecture — that the laws of quantum mechanics allow for quantum computing, but that we can never build such a device — may be true. Building a quantum computer will certainly require huge advances in our ability to control quantum states, and shield them from unwanted interactions. But we have built exotic states of matter before (e.g. semiconductors) and I see no fundamental reason why we can’t make these advances.

In any case, as theorists it’s the strong version of the conjecture we really care about — do the laws of physics let us compute in BQP, or only BPP? If you believe the latter, you need to propose some new physics, which can be tested in the laboratory.

Loading...

Reply
- Gil Kalai permalink
  
  January 30, 2012 2:03 pm
  
  Thanks for your interesting post, Chris. I suppose some of your points will be discussed later. Here are some comments about a few of them:
  
  “In particular, the claim that there is a fundamental limit on entanglement implies that quantum mechanics, as we currently believe it, is false:”
  
  First , to be precise, we talk about limits for entanglements achievable by quantum computers. Second, we both do believe in such limits: for example both you and I believe that a quantum computer on n qubits cannot achieve a state described by a random unitary operation on all the qubits. This does not make us skeptics of quantum mechanics, right?
  
  Just to make it clear: I do not believe in any nonlinearities in Schrodinger equation. I am not a skeptics of quantum mechanics and if my conjectures are in conflict with QM I will happily admit that they are wrong. If you are interested to engage in a conversation with somebody skeptics of QM you need to find somebody else.
  
  QM is a mathematical language of noncommutative probability which allows (in principle) to formulate further layers of laws of physics needed to describe our world. It does not allow to derive all the laws and facts about our physical world. So my view is that QM itself accomodates the possibility of (universal) QCs and it also accomodates the possibility that QCs are impossible. And the second possibility should be explored.
  
  Correlation over very large distances will reflect entanglement over these large distances.
  
  Loading...
  
  Reply
  - Steve Flammia permalink
    
    January 30, 2012 2:45 pm
    
    “…both you and I believe that a quantum computer on n qubits cannot achieve a state described by a random unitary operation on all the qubits”
    
    I can’t speak for Cris, but let me clarify what I think most QC researchers would say to this. Yes, a quantum state *can* be prepared in a random state in the total Hilbert space. You will have to wait an exponential amount of time to prepare this, but there is no problem in principle. In practice, you will need to encode the state to protect it from errors, but this part is also true classically.
    
    If you wish to limit yourself to what is achievable in polynomial time, then that’s okay too. You can prepare states using unitary t-designs for t ~ poly(n), so that with a polynomially large number of copies of the state, the statistics you get from measuring them would be indistinguishable from the t-th moments of the Haar measure. Preparing these states takes a polynomial amount of time on a quantum computer. So in a rather strong operational sense, these states are indeed random.
    
    Loading...
  - Cristopher Moore permalink
    
    January 30, 2012 6:20 pm
    
    Gil, I’m still confused. You said:
    
    “First , to be precise, we talk about limits for entanglements achievable by quantum computers.”
    
    I take it by “quantum computer” you mean a physical system that can make a series of simple unitary operations. Such things certainly can generate arbitrary amounts of entanglement, and do so efficiently.
    
    “Second, we both do believe in such limits: for example both you and I believe that a quantum computer on n qubits cannot achieve a state described by a random unitary operation on all the qubits. This does not make us skeptics of quantum mechanics, right?”
    
    Well, as Steve says there are pseudorandom states that we can achieve efficiently, and that are highly entangled. So I still believe that the claim that we can’t achieve high degrees of entanglement (even with a series of poly(n) unitary operators, each of which only couples a constant number of qubits) is inconsistent with QM.
    
    Loading...
  - Boaz Barak permalink
    
    January 31, 2012 8:09 am
    
    Gil, related to Steve’s reply,is it the case that according to your conjectures there are certain quantum states that simply cannot be (approximately) generated, even in exponential time, and even for small values of n (maybe even n=2)?
    
    Loading...
  - John Sidles permalink
    
    January 31, 2012 11:52 am
    
    Closely related to Boaz’ excellent and very natural informatic question, “Are there certain quantum states that cannot be (approximately) generated?” is its thermodynamically dual question “What is the entropy function of a quantum dynamical system in which certain states cannot be (approximately) generated?”
    
    It was Gil himself who (implicitly) suggested this latter question, in his recent Theoretical Physics StackEchange question “Onsager’s Regression Hypothesis, Explained and Demonstrated” … certainly Gil’s TPS question relates very naturally to core issues of this wonderful Kalai/Harrow debate.
    
    These entropic issues are subtle at the classical level (via the Boltzmann entropy function), and they are even subtler at the quantum level (via the von Neumann entropy function). Thus it is far from obvious (to me) what “Kalai entropy function” might describe the thermodynamical behavior of qubit systems for which Kalai’s Conjectures 1–4 hold true.
    
    Prior to grappling with this tough class of problems, younger researchers in particular may wish to reflect upon David Goodstein’s celebrated introduction to his textbook States of Matter
    
    “Ludwig Boltzman, who spent much of his life studying statistical mechanics, died in 1906, by his own hand. Paul Ehrenfest, carrying on the work, died similarly in 1933. Now it is our turn to study statistical mechanics. Perhaps it will be wise to approach the subject cautiously.”
    
    With due regard for the sobering subtlety and difficulty of these fundamental informatic/thermodynamic questions — and yet with regard too for their immense fundamental and practical importance — the possible mathematical forms of a Kalai entropy function, and the physical interpretation of the thermodynamical potentials derived from it, is kind of problem that many folks (well, me anyway) would very much enjoy seeing discussed by Gil and Aram.
    
    Loading...
- John Sidles permalink
  
  January 31, 2012 5:50 am
  
  Christopher reminds us: The problem [with nonlinear dynamics] is that experimental searches for such nonlinearities have shown that they are either zero, or incredibly small.
  
  Christopher, as with most “no-go” statements, it is prudent to parse the assumptions with care. Let’s use the language of geometric dynamics to do that parsing. Thus we appreciate:
  
  (1) Experiments (to date) give us good reason to reject quantum dynamical theories that specify nonsymplectic flow on flat Kähler (i.e. Hilbert) state-spaces. And this is reasonable, because the Second Law fails to hold in these systems.
  
  (2) Experiments (to date) give us little reason to reject quantum dynamical theories that specify symplectic flow on nonflat Kähler (i.e. Hilbert) state-spaces. And this is reasonable, because the Second Law holds rigorously in these systems.
  
  We thus are led to seek dynamical manifolds on which global conservation laws hold perfectly, the Second Law holds rigorously, and local quantum dynamics pulls-back naturally. Such manifolds exist, and over the decades they have been called by various names, of which “product state” is presently among the most common.
  
  Unsurprisingly, product state-spaces have become immensely popular among quantum researchers: the arxiv server presently holds more than 5000 “product state” preprints, and their number is increasing rapidly with no upper bound yet apparent.
  
  What is interesting in the context of the present GLL discussion is that product states constitute a concrete class of physical theories in which quantum mechanics is respected locally and Gil Kalai’s Conjectures 1-4 are respected globally.
  
  Thus, two physically interesting and mathematically natural questions (which I take to be the main topic of this GLL post) are:
  
  (A) Are experimental state-spaces effectively product spaces?
  
  (B) Are experimental state-spaces rigorously product spaces?
  
  Pragmatically speaking, if we refer to the quantum literature, we see that Question A has been more-or-less settled: the short answer is “yes” — although obviously there is an immense body of research remaining to be done, and that research is associated to practical problems having global importance and great urgency.
  
  Question B remains open, and it turns out that the key issues are associated to the fundamental limits of informatic causality, spatial localization, and relativistic invariance … which are of course precisely the limits where Hilbert-space quantum dynamics encounters still-unresolved difficulties. The simulationist perspective on these fundamental quantum dynamical issues is (of course) evolving rapidly, and it is reasonable for younger researchers to foresee that later in the 21st century there will be GLL posts that are specifically concerned with these topics .
  
  Regardless of one’s opinion regarding Question B — which is such a deep, difficult, unsettled, and contentious question that opinions are as much a matter of faith as of physics — it is evident that Gil Kalai’s four conjectures help greatly to illuminate our practical understanding of Question A … and for setting forth these conjectures Gil surely is deserving of all of our appreciation and thanks.
  
  For all of the preceding reasons, it seems (to me) that this one of the best GLL posts ever! 🙂
  
  Loading...
  
  Reply
Craig permalink

January 30, 2012 1:48 pm

I had a thought that Heisenberg’s Uncertainty Principle is the result of the laws of physics being digital in the sense of Fredkin and Zuse:

Consider the relation, (delta x) times (delta p) >= h/4pi.

In a digital universe, there is a finite amount of memory in the computer controlling the universe, so it makes sense that as delta x gets small enough, the computer controlling the universe would run out of memory, forcing delta p to be bigger.

It is known that it is possible to derive the laws of quantum mechanics from Heisenberg’s Uncertainty Principle, so the digital physics hypothesis would explain why quantum mechanics has been found to hold true. http://arxiv.org/abs/quant-ph/0201084

Has my idea been proposed before?

I think the digital universe hypothesis as an explanation for quantum mechanics makes the most sense and I also think it implies that quantum computing on a large scale is impossible, as the “great computer in the sky” doesn’t have enough memory to perform it. What do you think?

Loading...

Reply
- aram harrow permalink
  
  January 30, 2012 2:15 pm
  
  I think you could say the universe is digital in the sense of being made of qubits, but not of bits. Bits don’t work because otherwise n particles would require exp(n) bits to describe, and also because of Bell’s theorem. But qubits are a perfectly fine way to discretize information.
  
  Loading...
  
  Reply
  - Craig permalink
    
    January 30, 2012 2:53 pm
    
    No, I mean bits. I claim that the “great computer in the sky” (most likely some type of cellular automata) wouldn’t be able to handle calculations for n particles in a digital universe when n is large, say n=1,000, because exp(n) would be too large. So quantum mechanics would fail for large entanglements in a digital universe. This is why I think large scale quantum computing wouldn’t work in our universe, because I think our universe is digital.
    
    The laws of quantum mechanics would only work for interactions between a small number of particles. For instance, the Young double slit experiment could easily be modeled in a digital universe by a cellular automata.
    
    Loading...
Stephen Lee permalink

January 30, 2012 2:58 pm

Correct me if I’m wrong, but aren’t you confusing two different thought experiments of Einstein. I hadn’t heard much of his criticism of BKS before, but that appears to a decade earlier than the ‘Clock in the box’ idea, which Bohr countered with an appeal to general relativity. I would add that the idea that that Einstein didn’t understand the consequences of his own theory isn’t really fair. The point is that just as there is a ‘position-momentum’ uncertainty, for a clock there is an ‘accuracy-mass’ uncertainty, which will turn up however you try to measure the mass.

Loading...

Reply
- KWRegan permalink
  
  January 30, 2012 3:58 pm
  
  You are right—having remembered Bondi and the Solvay 1930 debate and “perpetual motion”, I expected the Bohr-K-S reference (which 1-1/2 pages earlier says “Bohr had stung Einstein in BKS with one of Einstein’s great ideas”) to be the same thing. I’ve fixed it above, thanks. A recent description that’s probably “fairer” is this by Paul Davies, About Time.
  
  On the overall discussion, my take is that whether highly entangled (non-random) states can be created is not the issue. It’s the effort required to create them, and whether this creates a double-bind: Either they’re hard, or they’re easy enough that we may expect to find them plentiful in Nature, especially after long evolutions.This strikes me as something QC that’s not QM. I know Gil is saying some other things, and I have some other things too…in due time. Out of left field there’s also “quantum discord” said to give correlations without entanglement.
  
  Loading...
  
  Reply
- KWRegan permalink
  
  January 30, 2012 7:37 pm
  
  From Walter Isaacson, Einstein, p349 top re. 1930 Solvay: “It was one of the great ironies of scientific debate that, after a sleepless night, Bohr was able to hoist Einstein by his own petard. The thought experiment had not taken into account Einstein’s own beautiful discovery, the theory of relativity…Einstein forgot this, but Bohr remembered.” Apparently no mention of the BKS exchange.
  
  Loading...
  
  Reply
Anonymous permalink

January 30, 2012 3:14 pm

These conjectures would be new physical laws, but there is neither experimental evidence supporting them or known physical mechanisms that would explain them. All relevant experiments suggest the opposite, and any new physical mechanisms going beyond quantum mechanics would be bigger news than anything the LHC might ever find. Conjectures 3 and 4 would contradict relativity! The arguments seem to come down to quantum computers can’t exist because then factoring would be easy.

Factoring is easy.

Loading...

Reply
John Sidles permalink

January 30, 2012 3:52 pm

Oh boy! Gil and Aram are two researchers whom I respect greatly … so this is one debate that (IMHO) both sides are sure to win.

How can both sides win the debate? Easily … even naturally!

Suppose that an omniscient oracle revealed to us that Hilbert-style state-spaces are the state-spaces of Nature. Still it might happen that a Kalai-style (non-Hilbert) state-space might be (a) an excellent approximation to Nature’s state-space, and (b) far easier to simulate than Hilbert space.

Such Kalai-style physics in quantum dynamics might (for example) resemble von Neumann’s artificial viscosity in fluid dynamics. In practical computations von Neumann viscosity makes Navier-Stokes systems far easier to simulate, at the price of dynamical imprecision that is (for many purposes) entirely acceptable.

Since no such omniscient oracle is available, it seems entirely plausible (to me) that at the end of the 21st century, we will still be debating whether “Nature’s state-space is Hilbert yet practical simulation state spaces are Kalai”, versus “Nature’s state-space is Kalai, yet for theoretical convenience the Hilbert approximation is exceedingly useful.”

Elevator Summary: One plausible outcome of the Kalai/Harrow debate is (a) yes quantum computers will be feasible in the 21st century, yet (b) they won’t work by physics we are entirely sure of, or compute by algorithms that we presently conceive.

Loading...

Reply
- John Sidles permalink
  
  January 30, 2012 4:10 pm
  
  To be concrete, in seminars we teach our engineering students practical methods for compromise: we pullback the old testament of Hilbert and Dirac onto the new testament of Onsager and Kalai.
  
  Loading...
  
  Reply
  - KWRegan permalink
    
    January 30, 2012 8:21 pm
    
    Beautiful comparison chart. Meanwhile, I love the way Onsager’s gravestone, next to one listing many accomplishments of the deceased, says just “Nobel Laureate*” with the * added later by his children, and “*Etc.” below.
    
    Loading...
  - John Sidles permalink
    
    January 30, 2012 8:51 pm
    
    Yes, there are many famous Onsager stories: students called Onsager’s graduate-level course “Sadistical Mechanics”, for example!
    
    Loading...
- John Sidles permalink
  
  January 30, 2012 5:07 pm
  
  Hmmm … one further way to describe a Harrow/Kalai middle ground is this: The gods of mathematics have blessed us with an superabundance of dynamical state-spaces for which (a) well-established global conservation laws hold exactly, and (b) local dynamical flows pullback approximately, and (a) thermodynamical principles hold rigorously.
  
  So for the present, perhaps the question “Is Hilbert-space quantum mechanics the true state-space of Nature?” is too hard for us to be entirely confident of near-term progress (although surprises surely are welcome) … a more practical use of our energies may be to construct, survey and appreciate the (many!) exceedingly useful dynamical state-spaces with which (as a burgeoning arxiv shows us) our 21st century has been so abundantly and unexpectedly blessed.
  
  Needless to say, these middle-of-the-road views leave good reason to hope for a vigorous debate here on GLL between the “Kalaists” and the “Harrowites” … in the confident expectation that both sides will win! 🙂
  
  Loading...
  
  Reply
Oldrich Nos permalink

January 30, 2012 4:25 pm

Dear Sirs;
You can weather one more deluded. See my updated web site, section “perpetuum”
BOOK 3
Regards,
Oldrich

Loading...

Reply
Roger permalink

January 30, 2012 4:42 pm

The perpetual motion analogy is a good one. Quantum computer research keep claiming progress, but it is like the progress of free energy researchers. Yes, they may find some slight gain in efficiency, but the research says nothing toward showing that the goal is attainable.

It is just not true that the skeptics of quantum computing are really skeptics of quantum mechanics. All of quantum mechanics can be true without quantum computers.

Loading...

Reply
Boaz Barak permalink

January 31, 2012 7:45 am

Gil, I understand from this you believe that physically realizable quantum computers offer no superpolynomial speedup over classical computers, and hence there is a polynomial time algorithm to simulate them. Do you have a sense of what this algorithm is?

Loading...

Reply
- Gil Kalai permalink
  
  January 31, 2012 11:04 am
  
  Boaz, as you see in the post we mainly consider quantum error correction and do not discuss computational issues. Do you ask if quantum computers that satisfies Conjectures 1-4 can be simulated classically? (The answer is that I dont know.) Or is your question different?
  
  Loading...
  
  Reply
  - Boaz permalink
    
    January 31, 2012 12:49 pm
    
    Gil, I thought the whole point of this conjectures was to argue that the computational power of physically realizable quantum computers falls short of BQP. So, I’m just trying to understand if you think that their power is exactly like classical computers (i.e., the uncontrolled noise helps simulate them classically, perhaps somewhat analogously to the situation described in this paper), or you think that they are stronger than BPP but weaker than BQP. I guess the answer is that you don’t know.
    
    I would just comment that if the latter condition is true, then qualitatively it doesn’t change the “conventional wisdom” on quantum computers: they offer super-polynomials speedups over classical computers on some, but not all problems. Whether integer factoring is one of those problems is of course very interesting, but in some sense a question that is not so fundamental.
    
    Loading...
  - Gil Kalai permalink
    
    January 31, 2012 1:35 pm
    
    Dear Boaz, As is also mentioned in Aram’s remark, the feasibility of quantum error correction is in several respects closer to various questions in physics and may be more relevant to deep aspects of physics than the computational complexity issue. Probably my conjectures “should” push the computational power to BPP. We will discuss related things later.
    
    Loading...
  - Boaz permalink
    
    January 31, 2012 3:25 pm
    
    Thanks Gil – I’m looking forward to your future posts. I know very little about quantum noise models and error correction, so am using my (probably flawed) intuition from classical computation that in principle one should be able to reduce the noise to an arbitrarily low level which is some function of the budget you have to spend. I guess this is in sharp contrast to your Conjecture 1, and I’m very curious to understand this.
    
    I’m also wondering about your statement that you “do not expect a common physical reason why my conjectures should apply for each proposed realization of a QC”. To rephrase (combining this with your statement that the conjectures should push the computational power to BPP) it seems you’re saying that a classical computer can simulate in polynomial time every real-world quantum system, but there isn’t any unifying reason why this happens.
    
    Loading...
  - Gil Kalai permalink
    
    February 3, 2012 10:30 am
    
    Dear Boaz,
    
    Regarding the computational complexity aspect. It is possible that my conjectures (including a conjecture about noisy quantum evolutions which is in the papers and not in the posts) push the computational power of noisy quantum computers that satisfy them to BPP. This is largely because of the additional side effect of error-rate scaling up. But I am not sure about it. And I certainly cannot prove it.
    
    There are various subtle issues regarding computational power of quantum systems: It is an unproved conjecture that entanglement is needed for computational speed up; it is not clear that decision problems capture the full computational power of quantum computers; it is not even known if distributions achievable by depth 2 quantum circuits give computational advantage; It is not known that irreversible noisy quantum computation reduces to BPP and as a matter of fact I believe that under the standard noise models noisey irrevesible quantum computing allows factoring.
    
    Still it is possible that a definite result can be proven and perhaps the first step would be to prove that some combination of my conjectures reduce the computational power to BPP in the reveresible case. This would already be very interesting.
    
    If you just conjecture that quantum noise have crazy correlation without the effect on the rate then I observed that log depth quantum circuits survive. This falls well below BQP but still allows factoring!
    
    I dont see a connection between the claim that the noise will satisfy my conjectures but possibly for different physical reasons depending on the implementation to your assertion that if the conjectures imply a reduction to BPP there will be no unifying reasons for why, in this case, classical computer can simulate the quantum system. (The conjecture themselves if indeed sufficient to give BPP reduction will provide a unifying reason for all the systems satisfying them).
    
    Indeed a crucial aspect of the discussion is about the possibility to transfer several intuitions from classical computation to the quantum case. (Those are crucil issues about computation although not necessary belong to computation complexity.) We will come back to this.
    
    Loading...
Jim Blair permalink

January 31, 2012 7:56 am

The current issue of “Scientific American” has an article titled:
“Is Space Digital?”.

The article describes an experiment that might settle the question empirically.

Loading...

Reply
Gil Kalai permalink

January 31, 2012 9:00 am

There are still many interesting items on Chris’ first post. So I will comment slowly on those points that we do not plan to discuss later, and some subsequent remarks.

1) “The weak version of Gil’s conjecture — that the laws of quantum mechanics allow for quantum computing, but that we can never build such a device — may be true.”

Chris, This is more or less the strong interpretation/version of the conjectures not one of the weaker ones. (Of course, my conjectures refer to specific properties of noisy quantum systems, and not just to a prophecy if QC will be built or not.)

2) “I take it by “quantum computer” you mean a physical system that can make a series of simple unitary operations. Such things certainly can generate arbitrary amounts of entanglement, and do so efficiently.”

Yes, I referred to a “realistic noisy quantum computer” namely a physical system that can make a series of simple unitary operations under realistic noise assumptions. Indeed this is the crucial question if realistic noise model allows arbitrary amount of entanglement (In the sense of Conjecture C, say). Standard noise models (and of course the noiseless model) do allow.

3) I somehow disagree with Steve’s statement that the state approximating the action of random unitary operator on all our qubits can be built in principle from local operators (But this can be a semantic matter). We have limitations on the states we can realistically generate by a computational principle.

Similarly the standard models of noise also give some limitation to states that can be generated. These limitations are consequences of further assumptions which are not part of the “laws of quantum physics”. For the standard noise models these limitations restrict the states that we can generate but not the computational power. So to Boaz’s question, even standard noise models restrict the type of states we can generate (also for a small number of qubits).

…Unless you mean by “we can generate” also what can be generated with exponentially small probability.

…Or unless you refer to encoded states, in certain senses. (What do you mean?)

(I am traveling so I will return to Boaz’s question, and other items on Chris’s, and questions later in the discussion in a couple of days).

Loading...

Reply
- Cristopher Moore permalink
  
  January 31, 2012 12:09 pm
  
  Gil, one of my difficulties with your conjectures is that physics (even QM) doesn’t have noise per se: it has lots of physical processes, and interactions with the environment, some of which we can control in practice and some of which we can’t (and this boundary is constantly moving as engineering improves).
  
  I think you agree that in a noiseless situation, we can generate states that are arbitrarily entangled. We also know how to defend against noise that is independent. So you are making a conjecture that in every real system, there are highly-correlated sources of noise that will prevent us from making highly-entangled states and doing long-term quantum computation. Why in the world would this be true? Where does this noise come from? What physical processes generate it?
  
  Syntactically, your conjecture seem to be a bit like this: “We know that the laws of hydrodynamics could, in principle, allow for heavier-than-air flight. However, turbulence is very complicated, unpredictable, and hard to control. Since heavier-than-air flight is highly implausible, we conjecture that in any realistic system, correlated turbulence conspires to reduce the lift of an airplane so that it cannot fly for long distances.”
  
  Forgive me for poking fun, but doesn’t that conjecture have a similar flavor?
  
  Loading...
  
  Reply
  - John Sidles permalink
    
    January 31, 2012 12:43 pm
    
    Christopher, I have taken the liberty of lightly amending your example as follows:
    
    “We know that the laws of plasma dynamics could, in principle, allow for practical fusion reactors. However, plasma turbulence is very complicated, unpredictable, and hard to control. In practice, correlated instability modes conspire to reduce confinement times such that fusion energy-gain is far less feasible than originally conceived.”
    
    And this amended example happens to be true.
    
    The great 20th century Soviet plasma physicist Lev Artsimovich was fond of assuring the public: “Fusion will be there when society needs it.” Well, now in the 21st century we need clean power urgently … and fusion power not here. This is a concrete and sobering lesson in how easy it is for a large scientific community (with undoubtedly the best of intentions) to seriously underestimate the dynamical subtleties of noise, instability, and chaos.
    
    As an emerging STEM discipline, quantum systems engineering is about much more than computing processes, and seeks to solve problems more urgent than decryption. To the extent that Gil’s conjectures 1–4 remind us of how easy it is to underestimate the effects of noise, instability, and chaos, these conjectures are providing valuable service.
    
    Loading...
  - Gil Kalai permalink
    
    January 31, 2012 5:16 pm
    
    Chris, I think that the heavier than air flight example is perfectly reasonable. There are various such examples, some went this way and some went that way, and some are still undecided. It his hard to make definite conclusions from analogies of this kind.
    
    I think, if I may, that conjecture 1 is interesting, as it sais things about states that can be experimentally created or that people are working on creating. You need not except it as a conjecture about how things are always are. You can simply think about it as a conjecture on how things are for processes that do not enact fault tolerance. This is relevant because there is no reason to assume that current experimental processes involve QFT mechanism. I think this is a different way to think about noise models for specific states of interest.
    
    you asked:”where this noise comes from” the proposed answer is that unless you interfere with the process this is how the noise will look like (independent noise need to be supressed in order to create these states).
    
    The issue of your first paragraph that physics does not have noise per se is interesting. I am quite interested what experts think about it.
    
    Loading...
Robert Alicki permalink

January 31, 2012 4:00 pm

As my name was mentioned by Gil I think, I should present my view on the discussed issue.
First of all, I like the title of this debate corresponding to my last preprint on this topic – “Quantum memory as a perpetuum mobile of the second kind”, because I believe that impossibility of fault-tolerant quantum computations (FTQC) should follow from the existing, perhaps refined, laws of thermodynamics. However, we do not have a universal proof of the second law of thermodynamics but a large and convincing body of partial results for the classes of idealized physical systems. Similarly, we can only analyze the existing evidence for two types of quantum computation models (I think that all schemes of quantum computations are isomorphic, including their problems)

I) Standard theory of quantum circuits with “threshold theorems”.

Here, the phenomenological models of noise are drastically oversimplified. Everyone, who tries to (properly) derive quantum master equations for quantum open systems can see that the terms describing the irreversible effects of environment depend not only on the environment’s parameters and the coupling of the system to environment but also on the system’s Hamiltonian. The more complicated (more “entangling”) is the self-evolution (“algorithm”) of the system the more involved is the response of the environment (“noise”). This is also true for quantum circuits described in terms of time-dependent Hamiltonians and can be seen as a physical counterpart to Gil’s conjectures. Notice that this effect is missing for classical systems. To describe the influence of a heat bath it is sufficient to add a friction force and the white-noise Langevin force, both independent of the system’s Hamiltonian.

II) Self-correcting systems (e.g. topological)

For these models (because of absence of “wave propagation”) one can rigorously derive Markovian master equations describing thermal noise and rigorously analyze the relaxation processes. For example, one can prove that:

1) There exist encoded qubits which are stable in the sense that their life-times grow exponentially with the size of the system (4D-Kitaev model, and others). The mechanism of stability is essentially classical – “macroscopic” free energy barriers between different states, below certain critical temperature.

2) For some models one can transversally realize some of the basic gates on encoded qubits.

However, one cannot even design a quantum memory using the above stability properties. Namely, the (transversal) gates realized as continuous operations driven by certain local Hamiltonians interfere with the protecting mechanism and produce irreversibility. I think that there is a universal (thermodynamical?) conflict between stability of encoded information and reversibility of the gates. It does not harm classical computations which are based on irreversible gates but is deadly for the quantum ones which need unitary gates.

Summarizing, there is no hard evidence, neither theoretical nor experimental, in favor of FTQC, on the contrary the analysis of existing models suggests its unfeasibility. Nevertheless, the criticism of FTQC is strongly suppressed by the community. One can find the wildest speculations published in the most prestigious journals, while even well-motivated criticism is usually rejected. The King is naked!

Robert Alicki

Loading...

Reply
- KWRegan permalink
  
  January 31, 2012 4:54 pm
  
  Thanks! Here’s a link to your perpetuum mobile preprint, which I somehow missed while going through your arXiv list to add links to Gil’s original draft. This was before Dick suggested the PMM analogy.
  
  Loading...
  
  Reply
John Sidles permalink

January 31, 2012 4:49 pm

Robert Alicki asserts: “Criticism of FTQC is strongly suppressed by the community.

This assertion calls to mind numerous parallel assertions along the lines of “plasma instability modes $\Leftrightarrow$ fusion reactor community”; “epigenomic regulation $\Leftrightarrow$ genomic community”; “tomography $\Leftrightarrow$ radiology community”; “Onsager theory $\Leftrightarrow$ thermodynamics community”; “density functional theory $\Leftrightarrow$ quantum chemistry community”; “KAM theory $\Leftrightarrow$ ergodic dynamics community”; “sociobiology $\Leftrightarrow$ sociology community”.

One wonders whether substituting “under-appreciated” for “strongly suppressed” might foster a more productive mind-set for the QM/QC/QIT community?

Certainly we have the inspiring personal examples, and the wonderfully innovative mathematical toolsets, of Kolmogorov, Onsager, Wilson, Arnol’d (etc.) to assure us that beautiful mathematics and physics reside within noise, instability, renormalization, and chaos … and we can be confident that further rich discoveries and wonderful practical applications await our persistent inquiry.

Moreover, it is entirely conceivable (and to my mind, even likely) that the societal benefits that already are associated to our QM/QC/QIT-inspired understanding of noise, instability, chaos, and simulation algorithms (etc.) are already comparable to (and may even exceed) the foreseeable benefits that quantum computing technologies are ever likely to provide.

Thus, one productive path forward is not a confrontational opposition between quantum computing skeptics and nonskeptics, but rather a mutually inspiring partnership.

Loading...

Reply
a permalink

January 31, 2012 6:16 pm

To the question “Is a quantum computer feasible?” – Didn’t they build a clunky machine which said 15 = 5 x 3?

Loading...

Reply
Geordie permalink

January 31, 2012 6:45 pm

They also built a beautiful machine that computed R(3,3): http://connect.arc.nasa.gov/p38z3xb8x5t/?launcher=false&fcsContent=true&pbMode=normal

Loading...

Reply
- John Sidles permalink
  
  January 31, 2012 7:34 pm
  
  Please let me be among the first to acknowledge and congratulate you, your colleagues, and the D-Wave Corporation, on the achievements that are reported in the recent arxiv preprint “Experimental determination of Ramsey numbers with quantum annealing” (arXiv:1201.1842). Perhaps the era of “quantum computers that are feasible in the 21st century, that work by physics we aren’t entirely sure of, and compute by algorithms that we don’t presently conceive” … is arriving sooner than many expected? In any case, congratulations!
  
  Loading...
  
  Reply
Geordie permalink

January 31, 2012 7:39 pm

Thanks John. BTW I side with Gil in the debate going on here, but for different (but related) reasons. The ideas underlying the circuit model of quantum computation are not good ideas, and I don’t think useful quantum computers based on circuit model ideas will ever be built. But this doesn’t mean that using quantum mechanics to make better computers won’t work.

Loading...

Reply
- John Sidles permalink
  
  January 31, 2012 8:07 pm
  
  Geordie, I agree with much of what you say — and I appreciate vigor in exposition too — but have a concern that blanket assertions like “the ideas underlying the circuit model of quantum computation are not good ideas” may obstruct / distract / confuse students (in particular) from appreciating that all the attendees at this scientific banquet are bringing good ideas to the table.
  
  Loading...
  
  Reply
- Marcin Kotowski permalink
  
  January 31, 2012 8:10 pm
  
  “The ideas underlying the circuit model of quantum computation are not good ideas, and I don’t think useful quantum computers based on circuit model ideas will ever be built.”
  
  Can you substantiate?
  
  Loading...
  
  Reply
Geordie permalink

January 31, 2012 9:52 pm

@John & Marcin: let me give you four simple examples of why the circuit model is not a good model for building quantum computers. (1) during a circuit model computation, the Hamiltonian for most of the qubits is designed to be zero. This means that for these qubits, the noise term in the Hamiltonian dominates their dynamics. For the majority of the qubits for the majority of a computation, the dominant term in the Hamiltonian is the noise term *by design*. This is a bad idea. The underlying reason for the inherent stability of the adiabatic model against noise is that in the adiabatic model the Hamiltonian of the computation is always, or nearly always, dominant over noise. (2) the gate model tacitly assumes that decoherence is basis independent. This is not the not way real / open quantum systems behave. In open quantum systems, there is a preferred basis — the energy eigenbasis. The definition of things like T_1 and T_2 is relative to the energy basis. While in a circuit model algorithm you are expected to be able to create arbitrary superpositions of states in any basis (usually written explicitly in the readout basis but you can also write these in the energy basis), superpositions of energy eigenstates decohere extremely quickly (this is what you measure when you measure T_2 for example). However this does not mean that superpositions in other bases decohere quickly. For example, if you have an entangled ground state and the energy gap to the first excited state is much larger than the other energy scales (like temperature), the entanglement in that state is an equilibrium property of the system, and persists for a long, long time — even if the system would decohere very quickly if you attempted to create a superposition of the ground and first excited states a la circuit model. (3) the circuit model requires high frequency, high precision signals to perform gates, and you need to be able to apply a large number of these. This is a huge practical issue. If all you care about is the ultimate computing power of the universe (maybe) you don’t need to worry about this. But this one will forever prevent, say, superconducting based circuit model quantum computers from being built. There are no ways known of getting millions of fully programmable microwave lines into a superconducting chip. (4) quantum error correction protocols vastly blow up the physical resource requirements into territory that makes absolutely no sense. while again it may be possible in principle to do this, in practice it’s simply a bad use of precious resources when there are other more effective ways to use quantum mechanics to build better computers. the amount of additional control circuitry and associated peripherals you need to implement even simple quantum error correction is really ludicrous. Sometimes people think that the main cost is simply the number of qubits — say multiplying the number of qubits by 7^3 or something. But that is not nearly the whole cost. You also need all of the high frequency, conditional control + active circuitry + all of the circuits to couple the qubits + etc. etc. etc. in order to make the whole thing work. Could you do this? yes, if what you mean is “in principle”. In practice? no. This type of system is like a ladder to the moon. Do any of the laws of physics prevent us from building a ladder to the moon? I don’t think so. Will we ever build one? No, because there are much better ways to get to the moon.

Loading...

Reply
- John Sidles permalink
  
  February 1, 2012 11:05 am
  
  Geordie, as I read your post I found myself nodding my head and repeating the punch-line of a centuries-old Judaic joke: “You know, Geordie is absolutely right!”
  
  And therefore, we all can be confident (or at least hopeful) that the Great Truths that your post has voiced, and that D-Wave’s achievements have demonstrated, will be matched by Great Truths in posts-to-come by older-school QM / QC / QIT researchers.
  
  By the process of this debate, we may all expect (or at least be hopeful) that the “dual” in “dualing quantum narratives” will transmogrify from the adversarial dualing of formal debate to the creative duality of formal mathematics.
  
  This is why, for purposes of catalyzing creative enterprises, plenty of folks (and I am one of them) have a particularly high regard for the complexity class that contains Calvinball. 🙂
  
  Loading...
  
  Reply
Joe Fitzsimons permalink

February 1, 2012 6:23 am

Gil’s conjectures appear in danger of falling into the trap of forbidding classical computation. In particular, conjecture 4 seems to be demonstrably false (the conjectures are somewhat ill-defined as written here, so perhaps Gil means something different than I am taking them to mean).

To see this note that we can choose a basis on the Hilbert space such that subsystems are defined non-locally. We can do this in such a way as to assign maximally entangled states in the new separation into subsystems to classical basis states. For example we can choose the 4 EPR states as corresponding to each of the 4 possible 2 bit strings so that classical errors still correspond to 1-local errors. Similarly we can choose a partitioning into subsystems of an n qubit string such that all classical strings were taken to represent the superposition of that string + its negation with the phase determined by the first bit of the string. Such a representation yields maximally entangled states (with respect to that basis) which are only subject to errors (which remain 1-local) via classical bit-filps. Thus conjecture 4 is demonstrably false when applied to such a partitioning.

However to exclude such partitionings is to exclude classical computation on with entangled energy eigenstates, which is contradicted by virtually all classical computers we have. The coupling Hamiltonian which makes materials stick together also almost universally produces an entangled ground states. Indeed electrons in solids are virtually always in extremely entangled states with respect either to the atomic energy eigenstates or spacial modes.

The reason why classical computing works, and quantum computing is usually hard, is due to the fragility of superpositions with respect to dephasing noise relative to the robustness of energy eigenstates. However the assumption that this corresponds to unentangled states is demonstrably false: many molecules exist with extremely entangled states even at high temperature. A simple example of this is the ground state of an Heisenberg antiferromagnet. Even for two spin qubits this has a maximally entangled ground state. Further the coupling in such systems is very often extremely strong compared to its coupling to the environment.

Loading...

Reply
- Gil Kalai permalink
  
  February 1, 2012 4:44 pm
  
  Dear Joe,
  Thanks a lot for the comment. The issues
  
  1) Do my conjectures (or perhaps even any similar attempt) cause classical computers to fail?
  
  2) Why is it that classical error correction (and computing) is so easy and common and quantum error correction (and computing) is so hard?
  
  Will be central to our continued discussion.
  
  For a rigorous and most recent formulation of the conjecture You may look at my paper http://gilkalai.files.wordpress.com/2009/12/qi.pdf (when noise accumulates) (Unfortunately the numbering of the conjectures has changed but it will be easy to be traced.)
  
  Your example regarding Conjecture 4 (of this post) is **very interesting** and I will do my best to understand it. If true it shows at the very least that something is very wrong with the formulation of that conjecture. However, please do explain it in more detail and also please look at the formal Conjecture, and , in particular, at the meaning of “highly entangled state”.
  
  Also, what do you refer to as “maximally entangled states (with respect to that basis)”?
  
  In your last paragraph, I am not sure that when you talk about “extremely entangled states” you mean what I mean. For example, in what sense are the molecules you mention “extremely entangled”? This is also very interesting.
  
  “The reason why classical computing works, and quantum computing is usually hard, is due to the fragility of superpositions with respect to dephasing noise relative to the robustness of energy eigenstates.”
  
  I suppose we would like to have an exlanation which is not based on the distinction between bit flip errors and phase errors. This distinction is based on some symmetry breaking which itself should be explained.
  
  Loading...
  
  Reply
  - Joe Fitzsimons permalink
    
    February 1, 2012 11:34 pm
    
    Hi Gil,
    
    Thanks for your response. I think it is only fair if I read the paper you mention to be sure we are talking about the same thing, so I will try do so later today.
    
    What I was trying to get at is that entanglement is only defined once we pick a particular partitioning of our system into subsystems. Without such a partitioning you merely have at most a superposition and even this depends on your choice of basis of basis. This may seem trivial, but there are often more than one natural partitioning of the system, and whether or not you have entanglement is merely a matter of what you choose to label as subsystems.
    
    An obvious example of this is a single photon put into a superposition of two modes. This is often used in linear optics implementations to encode a single qubit (and hence is a pure state of the single qubit, hence no entanglement). However you can also consider the occupancy number of the two spatial modes as defining the subsystems, in which case you can easily have a maximally entangled pair, and indeed it is rather simple, experimentally, to make rather complicated entangled states in this representation using only a single photon and many modes. This is simply an interferometer, and is much easier to build than a full quantum computer, but as per Scott’s recent paper is probably not efficiently classically simulable.
    
    My point here is that entanglement is not necessarily the hard part of quantum computing (in this case the problem is performing non-linear gates), and so I believe making conjectures which have entanglement as a key part is destined to fail, since entanglement itself is not an intrinsic property of nature. It is something we impose on nature by choosing a representation for our information (in terms of choosing whether and how we subsystems), and there is often more than one reasonable way to do this. Indeed, decoherence isn’t even the current limiting factor in several implementations, including many optical implementations, so it on its own doesn’t seem to be a full explanation for why we have not yet made more progress.
    
    However, I just want to add that I agree with your last point. Phase flips are relevant for some systems, but it is only part of the picture, and doesn’t really tell the whole story. There are many systems where such an error model does not apply.
    
    Lastly, I’d like to say that I find the 1st question you mention (“Do my conjectures (or perhaps even any similar attempt) cause classical computers to fail?”) to be very interesting. Indeed, it makes me wonder whether it might be possible to prove something along these lines. This may seem a fools errant, since generally classical computing is deemed to be immune from phase errors, but this isn’t really true. This is something that seems obvious when you treat a classical computer classically, however it is fundamentally false. Whether or not we may like to believe it, classical computers are still governed by quantum mechanics, and sufficiently strong dephasing noise will simply freeze them via the quantum Zeno effect, and even at lower levels will lead to incorrect transitions between states (I won’t say bit flip errors, because most classical computers represent bits with systems that can be in far more than 2 states).
    
    In any case, I have found the debate so far very interesting (if somewhat infuriating, as I find it hard to understand what could possibly lead someone knowledgeable in the area to conjecture that building a quantum computer is impossible), and will follow the series with much interest.
    
    Loading...
  - Robert Alicki permalink
    
    February 2, 2012 7:37 am
    
    ” I have found the debate so far very interesting (if somewhat infuriating, as I find it hard to understand what could possibly lead someone knowledgeable in the area to conjecture that building a quantum computer is impossible), ”
    
    In my case the answer is simple : 35 years of experience in the theory of quantum open systems which exactly deals with quantum noise, decoherence , stability etc.
    
    Loading...
  - Gil Kalai permalink
    
    February 2, 2012 2:12 pm
    
    Dear Joe, maybe the following remark on Conjecture 4 could be helpful.
    
    Conjecture 4 refers to highly entangled states of n qubits. It should certainly applies to states which occur in quantum codes, or in basic quantum algorithms. More formally we want that the state to demonstrate 2-particle interaction for every (or for most) pairs of qubits. To define it formally we cannot just talk about 2-qubits entanglement so the way to do it is to demand that if you measure every n-2 qubits and look at the outcome, the expected entanglement of the pure joint state for the remaining 2 qubits will be large. (The papers give mathematical formulations.)
    
    Loading...
  - Joe Fitzsimons permalink
    
    February 3, 2012 12:25 am
    
    Hi Gil,
    
    So when you say “highly entangled” you are referring only to states on maximal Schmidt rank? These are the only states which exhibit entanglement between every pair when the remaining qubits are measured. If you want to make that entanglement significant, than you also need to have the amplitude for each branch approximately equal in amplitude, but I guess this is less important. What’s particularly strange is that such states are more robust against noise than states of low Schmidt rank such as the GHZ state, in the sense that entanglement can remain even in the presence of quite significant noise (see quant-ph/0004051 for example).
    
    Loading...
  - Gil Kalai permalink
    
    February 3, 2012 8:36 am
    
    hi Joe, So is your counterexample still survives with this interpretation of “highly entangled?” (The various notions you mention are not sufficiently fress on my mind to tell on the spot if this is the same definition. But if it, is it is certainly a better way to formulate it.)
    
    Loading...
  - Joe Fitzsimons permalink
    
    February 3, 2012 10:35 am
    
    Hi Gil,
    
    Well, I didn’t have your exact definition in mind when I made the comment. To be honest, I’m not sure that there is any stabilizer state with Schmidt rank n-1, though if there was this would provide a counter example. Linear graph states have Schmidt rank floor(n/2). Under Z errors these form a complete basis, with X errors are equivalent to at most pairs of Z errors, and Y errors equivalent to at most tripplets of Z errors. Labeling this with computational basis states such that the bitstring corresponding to the number of Zs applied at each vertex (i.e. 0 or 1), we would then have an entangled state where any error leading to an orthogonal state would correspond to a set of bit flip errors with weight at most three times the weight of the original error.
    
    However, you may object that such a state does not have Schmidt rank n-1, which is equivalent to your definition when considering qubits as the local system. As I mention above, I’m not sure that it is possible to pick a graph state as an example. However if you do pick the maximally connected graph and replace all controlled-Z gates in the constructive definition (in which qubits are prepared in the pus state and then have controlled-Z gates performed wherever there is an edge in the corresponding graph) with weaker controlled-phase gates (say associated with the angle theta), then you should get a state with Schmidt rank n-1. Again, local Z operators applied to this form a complete basis. X operators are equivalent to Z rotations on neighbouring qubits through the angle theta associated with the controlled-phase gate applied, and hence if it is weak are essentially equivalent to slightly increased uncorrelated noise in the neighbouring qubits. In any case, associating these weighted graph state basis states with the computational basis states as before (i.e. via the combination of Zs required to produce a given basis state) again leads to a situation where correlations in the noise in one basis lead to correlations in the noise in the other basis and uncorrelated noise in one basis corresponds to only slightly correlated noise in the other.
    
    Loading...
- Gil Kalai permalink
  
  February 3, 2012 2:42 pm
  
  Dear Joe,
  
  your suggestions are interesting. But I don’t think that your new tensor structure idea is relevant to the conjectures.
  
  My conjectures depends on the computational basis which is required for the definition of the qubits and gates. In particular, they depend on dependent errors for gated qubits.
  
  The setting for Conjecture 3 is this:
  
  We have a noisy quantum computer where we assume (like in the standard model of noise) that when we create a pair of entangled qubits by a gate then the errors are of arbitrary form. Lets restrict ourselves further to the case that there are gates acting on one and two qubits and that the 2-qubit gates induce substantial positive correlation for the probability that the two involved qubits be corrupted.
  
  Quantum fault tolerance allows you to start with such noisy entangled pairs and create pairs of entangled qubits with almost independent errors.
  
  We want to identify crucial properties of noisy systems for which QFT fail.
  
  QFT can fail from several reasons such as:
  
  1) The computer program does not enact quantum fault tolerance,
  
  2) the error-rate is above the threshold of the threshold theorem,
  
  3) Crazy properties of noise
  
  And the way we propose to test such a failure is that the property “positively correlated noise for entangled qubits” is carried also to pairs of entangled qubits which are created along the computation. This is the context of Conjecture 3.
  
  The rational of Conjecture 4 is that for highly entangled states, Conjecture 3 (or a somewhat stronger form) will say that each pair of errors are substantially positively correlated and this implies error shynchronization.
  
  Of course, if our system has gates which create pairs of entangled qubits with independent errors to start with, then we cannot expect the conjecture to hold. The conjecture is an amended behavior of the standard model of noisy quantum computers.
  
  In your construction you replaced the tensor power structure by another tensor power structures so now the states are entangled to start with and you don’t need noisy 2-qubits gates at all to create entanglement. This does not seem relevant to us. (And I dont think it violate the mathematical formulation of the conjectures.) Again, we start with a quantum computer where the only way to create entanglement to start with is via gates acting on 2 or more qubits.
  
  Anyway, it will be best to check your idea for Conjecture 3 on a small number of qubits.
  
  Loading...
  
  Reply
  - Joe Fitzsimons permalink
    
    February 4, 2012 8:44 am
    
    Hi Gil,
    
    My point was that there is often more than one natural basis, and often there are two or more natural choices for the basis and subsystems where the basis states are entangled with respect to one another.
    
    If for example I have a set of strongly exchange coupled electron spins, do I consider spin states as the basis or do I consider eigenstates of the Hamiltonian? Both seem perfectly reasonable, both have been used in QC implementations, and pretty much any assignment of local subsystems to the Hamiltonian eigenstates will lead to each basis being entangled with respect to the choice of local systems for the other.
    
    Loading...
Robert Alicki permalink

February 2, 2012 3:27 am

Dear Colleagues,

one cannot understand the problems with FTQC in terms of flip of phase errors or even their generalizations to clusters of such errors for fixed number of qubits. Imagine a thermalization process of a quantum system with complicated Hamiltonian, i.e. with highly entangled eigenstates.
To drive such a system to an equilibrium (Gibbs) state, which is a mixture of those eigenstates, one needs a highly entangled (correlated) noise which contains error operators acting on the whole Hilbert space and not local flip or phase errors. The situation is completely different for classical systems, like those described by Ising Hamiltonians. Here the Hamiltonian eigenstates are product vectors and the Gibbs state can be easily generated by local flips (phase errors are irrelevant as they do not change the eigenvectors). This is the reason why the Metropolis algorithm is so successful in classical statistical mechanics but does not work in quantum. Only the combination of a truly quantum (entangling) computer’s dynamics with essentially classical model of errors can produce “miracles” like the threshold theorems in FTQC.

Loading...

Reply
- aram harrow permalink
  
  February 6, 2012 1:32 pm
  
  This is an interesting theory, even apart from the FTQC question. I think it’s a possibility, but I believe more in the possibility that interactions affecting a few terms at a time will still eventually drive the system to equilibrium. This is clearly possible with *some* sequence of two-qubit interactions; consider the quantum Metropolis algorithm of Temme et al.
  
  Another possibility is that systems are metastable and take exponentially long to reach their ground state.
  
  What I think is the more relevant possibility for quantum computing is that everything is far out of equilibrium, and work is continually performed to pump away errors and keep it that way.
  
  Is there a proposed mechanism that would produce highly entangled noise?
  
  Loading...
  
  Reply
- John Sidles permalink
  
  February 6, 2012 2:31 pm
  
  Is there a proposed mechanism that would produce highly entangled noise?
  
  Real-world external reservoirs commonly exhibit relaxation times ranging from seconds-to-minutes-to-hours and at the same time generically couple multiple quantum gates via Preskill-style $k$ -qubit interactions, and thus qualify sensu stricto as entangled noise.
  
  Well-known examples of non-Markovian multi-qubit noise mechanisms include thermal magnetic noise (in conductors), spin magnetic noise (in nuclear spin reservoirs), electrostatic noise (in insulators), patch effect noise (in conductors), to say nothing of (typically) slower noise processes associated to ionic transport (across permeable interfaces) and dislocation motion (in lattices). And yes, in our own QSE prototypes we commonly encounter all of these noise mechanisms (and more).
  
  These “schmutzy” interactions generically are associated to Hamilton flows that are (in Robert Alicki’s phrase) “not local flip or phase errors,” and that are nonstationary on time-scales of seconds to hours (or longer), so that these reservoirs remember for a long time the QC states that they have “seen” in the past. Moreover, even if we imagine a quantum computer fabricated of trapped ions floating in a dark cold optical cavity, still that optical cavity would be observed by (for example) detector/emitter diodes that (even when unpowered) couple their “schmutzy” conduction bands to the cavity modes, thus generating precisely the Preskill-style $k$ -qubit noise that is most fatal to scalable error correction (as presently conceived).
  
  Now, do these mechanisms represent fundamental obstructions to QC, or do they represent practical obstructions … or are they best regarded as enticing new opportunities for fundamental research in both physics and mathematics, and also for eminently practical new enterprises? Now those are four interesting questions, to which “plausibly”, “surely”, “definitely”, and “assuredly” are (to my mind) four reasonable answers.
  
  Loading...
  
  Reply
Scott Aaronson permalink

February 2, 2012 8:49 am

Just a quick remark

The “debate” format makes it seem like we have a conflict between two competing theories: one that says scalable QC is possible and one that says it isn’t. But that’s not the situation at all: this is a conflict between (a) a theory, and (b) attempts to poke holes in that theory, without proposing a replacement. This can be seen most clearly in the exchange between Gil and Boaz above. In response to Boaz’s extremely-pertinent question, of whether, if FTQC is impossible, that means there’s an efficient classical simulation of realistic quantum systems (and if so, what is it?), Gil basically says that he doesn’t know and prefers to focus on his Conjectures 1-4 casting doubt on FTQC. This sort of response might be fine in a legal defense (“if not my client, who DID commit the murder? who knows? maybe aliens, maybe the boogeyman. I don’t have to explain it, I just have to cast enough doubt on the prosecution’s case!”). But it’s more problematic in science, where we want to know what the world is LIKE, and where the modus operandi is to accept a model provisionally until it’s replaced by a better model. Right now, there’s a detailed picture of the world could be like such that QC is possible, but no serious competing picture of what the world could be like such that it isn’t. Obviously, that situation could change at any time, and while I don’t expect such a change, I would welcome it as the scientific thrill of my life.

Loading...

Reply
- Gil Kalai permalink
  
  February 2, 2012 9:09 am
  
  Dear all,
  
  A quick answer. I agree with what Scott writes in the first paragraph about the assymetry. This is a discussion between a theory and attempts to poke hole in that theory.
  
  Just to make it clear: the theory we discuss is *not* quantum mechanics, but the postulate that universal quantum computers are possible and its wonderful theoretic consequences.
  
  I promised Boaz to give some more detailed answer to his good questions about computational complexity and about sumilating classically realistic quantum systems. Please stay tuned.
  
  I realize that to say “I dont know” is not so scientific and indeed I commend Scott for never saying or even thinking anything like that.
  
  “Obviously, that situation could change at any time, and while I don’t expect such a change, I would welcome it as the scientific thrill of my life.”
  
  100,000$?, 10%?, something?
  
  Loading...
  
  Reply
  - Scott Aaronson permalink
    
    February 2, 2012 9:57 am
    
    Gil, pleading ignorance is fine, but if you want to be consistent about it, it seems to me that you should take the one explanatory theory we have and then be equally ignorant in every direction. I.e., “who can say what the complexity of simulating physics really is? Maybe it’s more than BQP. Maybe it’s less than BQP. Maybe it’s incomparable.” Note that strictly speaking, all three possibilities are perfectly consistent with QM (e.g., maybe there are powerful oracle unitaries available, or gigantic Hilbert spaces). What’s strange to me is focussing on one of these possibilities over the others.
    
    Loading...
  - Scott Aaronson permalink
    
    February 2, 2012 10:18 am
    
    BTW: sure, no problem. I hereby offer $100,000 for a demonstration, convincing to me, that scalable QC is impossible in the physical world.
    
    Loading...
  - Craig permalink
    
    February 2, 2012 12:12 pm
    
    Scott,
    
    That’s like offering $100,000 to anyone who can prove that Bigfoot doesn’t exist.
    
    Loading...
  - Scott Aaronson permalink
    
    February 2, 2012 12:44 pm
    
    Craig: No, I don’t think so. Whether Bigfoot exists is a question about the contingent history of evolution on Earth. By contrast, whether scalable QC is possible is a question about the laws of physics. It’s entirely conceivable that future developments in physics would conflict with scalable QC in the same way relativity conflicts with faster-than-light communication and the Second Law conflicts with perpetuum mobiles. It’s such a development in physics that I’m offering $100k for.
    
    Loading...
  - John Sidles permalink
    
    February 2, 2012 1:26 pm
    
    The meta-assertion “ ‘Scalable QC is possible’ is a question about the laws of physics” can be parsed in differing yet equally valid ways. Consider for example the parallel constructions ‘One-meter tokamak reactors are possible’ and ‘Alcubierre warp-drives are possible.’ A theoretician might regard all three statements as true (in certain well-posed circumstances), an experimental physicist might regard all three statements as posing wonderful challenges, and a systems engineer might regard all three statements as sufficiently unrealistic as to be effectively false — and some folks (me for one) would argue that in our present state of knowledge, all three opinions are reasonable.
    
    Loading...
  - Craig permalink
    
    February 3, 2012 3:13 pm
    
    Scott,
    
    You quote Leonid Levin in your PhD thesis. If you are looking for “future developments in physics would conflict with scalable QC in the same way relativity conflicts with faster-than-light communication and the Second Law conflicts with perpetuum mobiles”, then his criticism of scalable QC seems to me to be the answer you are looking for.
    
    The current laws of physics only hold for <= 12 decimal places as Levin said. Scalable QC goes out of this range, so it is in conflict with the current laws of physics. Of course, nobody has canonized this as a law of physics that has been taught in advanced courses in physics as far as I know, but it is a common theme in all physics experiments. Think about it. Why haven't scientists gotten past this problem of limited precision if finite precision wasn't a law of physics?
    
    A possible physical explanation of this limit is that the universe is discrete not continuous, but it doesn't really matter why, just that this is the way things are, just as Einstein's relativity and the Second Law are just the way things are, as far as scientists say they are.
    
    Similarly, it is possible to fold paper in half 12 times but probably not 13 times. http://pomonahistorical.org/12times.htm
    
    The fact that one can extrapolate a theory to ridiculous conclusions does not mean the ridiculous conclusions are true. It also doesn't mean that the ridiculous conclusions are science either. It just means that they are ridiculous conclusions. Scalable quantum computing is a ridiculous conclusion, based on current science, just as Bigfoot existing is a ridiculous conclusion, based on current science (except for a TV show I saw on it recently where scientists said it might be true).
    
    Loading...
  - Scott Aaronson permalink
    
    February 3, 2012 8:16 pm
    
    YAWN. I’ve answered that “argument” in many places—see for example page 6 of Multilinear Formulas and Skepticism of Quantum Computing. We can easily create states, in the lab, today, right now, that have amplitudes of 2^(-10000) or even smaller: to do so, just prepare 20000 independent qubits in the state (|0>+|1>)/sqrt(2)! That already makes it completely obvious that amplitudes can’t behave like energies or momenta or other observable quantities that we measure to a few digits of precision; they have to behave more like probabilities. (If you flip a coin 10,000 times, the laws of probability don’t start breaking down because the probabilities take too many digits to write down!)
    
    So then Levin is forced to say that, well, no, it’s not the number of decimal places in the amplitudes that he really meant to talk about, but some other property of the quantum state that somehow involves its complexity or entangledness. So what is that property, exactly? That question was precisely the starting point of my paper, which tried to address the question as sympathetically as possible but (I think, in retrospect) came up mostly empty. Anyway, the paper is full of simple observations about what I called the “Sure/Shor separator” problem; it might be helpful for skeptics to understand those observations if they don’t want to retread ground from 10 years ago.
    
    Look, I like and respect Levin a lot, but for ideological reasons, there’s no limit whatsoever to how howlingly-wrong he can be when it comes to quantum computing. There’s a reason why QC skeptics like Gil Kalai don’t bother to repeat the precision “argument”: because, presumably, they know full well that it doesn’t survive a moment’s thought!
    
    Loading...
  - Craig permalink
    
    February 4, 2012 7:50 pm
    
    Scott,
    
    I looked at your paper, particularly page 6.
    
    To make things more precise than Levin’s number of decimal places argument, I’ll state my hypothesis that scalable quantum computing should fail to yield any gain over classical computing, since this has never been demonstrated in a laboratory. This separates Sure states from Shor states as you defined them.
    
    Loading...
  - Scott Aaronson permalink
    
    February 5, 2012 6:29 am
    
    Craig, first of all, “gain over classical computing” is a property of computations, not of states. That already tells me you haven’t understood my paper at all. But more importantly, saying “QC should fail to yield any gain over classical computing” isn’t even an attempt to answer the Sure/Shor separator question: it’s just a restatement of the question! The question is: why does QC fail to yield a gain? Where does the breakdown happen? What physical property of all realistic quantum states would be violated by the states that occur in Shor’s algorithm? (And please don’t tell me the tautological property of “being useful for getting a computational speedup”—I know you think that, but presumably Nature doesn’t know or care what you’re using the state for, it just cares about some physical attribute of the state itself?) Do you recognize the urgency of these questions? Do you understand that the burden is on the QC skeptics to answer them?
    
    Loading...
  - Craig permalink
    
    February 5, 2012 6:08 pm
    
    Scott,
    
    The breakdown occurs because of an overflow error that you get when the complexity of a problem is too high, just as if you were to try to write the program for the latest version of Windows on a personal computer built in the late 1970’s.
    
    Nature just doesn’t have enough memory for exponential computations. There is no experimental evidence to suggest otherwise.
    
    I posted earlier why I thought this is true – because we live in a digital universe.
    
    But it doesn’t really matter why. Just that the evidence points to this being true.
    
    You have to be careful about extrapolation. Just because a theory is successful in making some crazy predictions doesn’t mean that the theory will be successful in making some crazier predictions.
    
    It’s better to look for another theory that makes only the crazy predictions, but not the crazier predictions.
    
    Loading...
  - Craig permalink
    
    February 5, 2012 6:30 pm
    
    Scott,
    
    Here’s another question which is easier, but I’d like to know your answer: When I was a kid, I used to experiment with the copy machine in my father’s office. I would make a copy of a picture, then make a copy of the copy of the picture, then make a copy of the copy of the copy of the picture, etc.
    
    I found that after about 6 copies, the original picture was unrecognizable. I assume that copiers are better today than they were then, but still I bet after a finite number of copies, the original picture would be unrecognizable.
    
    Yet, in theory, this still shouldn’t be. Do you think it is possible to build a copy machine in which after any n copies, the original picture will be recognizable? And what is the difference between this phenomenon and quantum computing?
    
    Loading...
  - aram permalink
    
    February 5, 2012 6:45 pm
    
    Craig, you might be confusing quantum computers with analog computers.
    
    This was an early source of confusion, which was addressed in the mid-1990s with the invention of quantum error correcting codes. These proved that quantum errors could be “digitized” just like classical errors. However, I think those insights are not widely known or understood.
    
    In the case of the photocopier, the answer is that a page of text written in English might slightly deteriorate with each copy, so simply rephotocopying each time. However, if you scan it, use OCR and print a new copy from it, then if this procedure works once it’ll work an unlimited number of times. (More accurately, a number of times that is exponential in the amount of error-correcting resources we use at each step.)
    
    Loading...
  - Ørjan Johansen permalink
    
    February 5, 2012 6:41 pm
    
    Craig wrote:
    
    Do you think it is possible to build a copy machine in which after any n copies, the original picture will be recognizable?
    
    Maybe have the copier embed a nearly-invisible error-correcting code into the copy, so that nearly no further deterioration will happen on later copies? Which sounds rather analogous what they’re trying to do with quantum computing.
    
    Loading...
  - Craig permalink
    
    February 5, 2012 10:39 pm
    
    aram,
    
    I’m not confusing the two. This is a separate question about photocopiers. Also, OCR only works for texts. I’m talking about copies of pictures here, in which OCR doesn’t work.
    
    Ørjan Johansen,
    
    Easier said than done. If it’s nearly invisible, the copier will not be able to read it. The copier can only read visible stuff. And if the copier embeds visible stuff into the copy, it’s not a copy. The copy machine must make a copy at each step and read the copy at the next step. Error correcting codes aren’t going to help us here.
    
    If you cannot create a copy machine that creates a perfect copy, then I don’t see how you are going to make large scale quantum computing work, as it seems to me that large scale quantum computing is more difficult.
    
    The relevant analogy here is that just as one can create of perfect copies of text, one can do small-scale quantum computing. And just as one cannot create perfect copies of pictures, one cannot do large-scale quantum computing.
    
    Loading...
  - aram permalink
    
    February 5, 2012 10:43 pm
    
    What you say would be correct if quantum computers were analog computers.
    However, quantum errors can be digitized, just like classical errors.
    And quantum information can be encoded in error-correcting codes, just like classical information.
    See this paper and the citing articles.
    
    Loading...
  - Craig permalink
    
    February 5, 2012 11:35 pm
    
    aram,
    
    But quantum computers are analog computers. The weights of each of the qubits are analog. You can do error-correcting codes for flipped qubits, but what if the weights have errors in them and the errors grow after each unitary operation? Then the quantum computing develops errors which cannot be corrected, similar to errors which develop in copying a picture.
    
    This doesn’t matter for equally weighted states – Sure states – since the errors have equal probability. But this does matter for Shor states.
    
    Loading...
  - aram permalink
    
    February 6, 2012 12:13 am
    
    Have you read the 1995 Shor article? Or subsequent work on QECC? (Any textbook on quantum computing would also suffice.)
    What you said was the prevailing view before QECC was invented.
    But QECC directly addressed this concern 17 years ago. Have you found a flaw in all those papers? Or just not noticed them?
    
    Not to pull rank, but before asserting that experts are wrong, it is polite to attempt to understand why they are claiming what they do, and not to first ask them to educate you about the basics of the field.
    
    In this case, here is a sketch of the reason why errors can be discretized.
    
    Let V be the subspace of (C^2)^{\otimes n} corresponding to a quantum error correcting code on n qubits. If it can correct one error, then V is orthogonal to each of the subspaces that results from applying sigma_i^{(j)} to V, where i ranges over {X,Y,Z} and j from 1, .., n. Also these subspaces should be orthogonal to each other. Thus if one error occurs (meaning one Pauli), then a measurement can figure out which one happened, and can undo it.
    
    What if each qubit is independently rotated in an unknown direction by up to an angle epsilon? Then the amount of weight in the single-error (correctable) sector is something like n epsilon, and for small enough values of epsilon, the probability of an uncorrectable error resulting from the measurement will be O(n^2 epsilon^2).
    
    Loading...
  - Robert Alicki permalink
    
    February 6, 2012 3:53 am
    
    Dear Aram, let me reply the question to Craig. I have read all the papers you mentioned.
    I spend few years (togather with Michal Horodecki, who is a young and brilliant guy, as you know) to uderstand the proofs of threshold theorems. We failled but at least we understood the assumptions. A mathematical theorem is only relevant for physics if its assumptions can be derived from the physical principles. All theorems in Quantum information are about simplified models and not about the fundamental theory (which in this case should be the quantum electrodynamics of electrons and nuclei ). Often a simple model is good enough to grasp the essence of the phenomenon. But for the FTQC theory, which deals with extremally subtle effects, all those neglected “tails” or “irrelevant contributions” can matter. I think , that the physicists like John Preskill understand very well this problem, and I appreciate very much their efforts to give a solid physical basis for FTQC. But up to know all those results are only partially succesfull. They change my initial attitude from “this is a pure nonsense, forget it” to “this is most likely a wrong idea, but an interesting challenge concerning the very fundamental problems of statistical mechanics and thermodynamics).
    At present there is a strong evidence supporting the picture of QC as a kind of analog computer. For example, complex quantum systems behave identically as classical chaotic systems what can be quantified using a version of Kolmogorov-Sinai dynamical entropy.
    Classical Newtonian physics, before the discovery of chaos, would also suggest the feasibility of extremally powerful classical analog computers based on continuous variables.
    
    Loading...
  - aram harrow permalink
    
    February 6, 2012 1:43 pm
    
    Robert, I take your objections seriously. Sorry for responding to Craig’s first; his were just more annoyingly uninformed.
    
    But I have to take issue with the very last point you made, which is that we needed chaos to tell us that Newtonian dynamics could not produce super-strong analog computers. In fact, if you posit an infinitesimal but constant noise rate (like 10^-20), then analog computing pretty clearly fails, even without knowing anything about chaos. In other words, even if we had never heard of chaos, we’d be able to notice our inability to prove a threshold theorem for analog computing that could cope with i.i.d noise.
    
    But the threshold theorem of quantum computers uses essentially the same assumptions as does the threshold theorem for digital classical computers. Yes, quantum systems can, in some cases, act chaotically, just as classical systems can. But I don’t see how you can say that this behavior is generic. Are superconductors chaotic? BECs? Lasers?
    And a classical RAM chip is still described by quantum mechanics: if it is chaotic, how does it store a bit so well?
    
    Loading...
  - Robert Alicki permalink
    
    February 7, 2012 9:24 am
    
    Dear Aram, you have raised a number of very interesting questions, some of them concerning still quite controversial issues. To address them honestly one has to write a book, but as the discussion becomes more and more interesting and substantial , I try to sketch my point of view. Sorry, for repeating myself, but certain issues are notoriously confusing.
    I believe more in the possibility that interactions affecting a few terms at a time will still eventually drive the system to equilibrium. This is clearly possible with *some* sequence of two-qubit interactions; consider the quantum Metropolis algorithm of Temme et al.
    Yes, but this is a quantum algorithm performed on QC and cannot be effectively implemented classically while classical Metropolis works very well for classical systems. The difference between quantum and classical is that flips of individual spins commute and are good error operators for classical systems. Therefore, the result of sampling does not depend of the order of applied errors (flips). For quantum systems the error operators do not commute even for such “ almost classical” models like Kitaev ‘s (R.A. et.al. J.Phys.A.42, 2008). Therefore, for quantum models we need additional averaging over the permutations in the sequence of errors what could be done efficiently only on QC.
    BTW, the fact that quantum error operators depend not only of the coupling to the bath but also on the Hamiltonian is appreciated only by a handful of experts. In hundreds of papers and dozens of books the authors simply add the convenient Lindblad generator to an arbitrary Hamiltonian. Some of them claim also that one can arbitrarily “design” Lindblad generators, e.g. to drive the system to the requested state.
    
    Another possibility is that systems are metastable and take exponentially long to reach their ground state.
    Why should it help FTQC?
    What I think is the more relevant possibility for quantum computing is that everything is far out of equilibrium, and work is continually performed to pump away errors and keep it that way.
    This is a very popular but wrong intuition. Imagine a system coupled to a bath at (almost) zero temperature which is driven to its (almost) ground state. The possible high initial entropy is reduced to (almost) zero but nevertheless the system ends in a unique final state i.e. does not contain any information about the initial input. What destroys information is not a high entropy alone, but also the always positive entropy production. Adding a non-equilibrium device like a refrigerator can reduce entropy but at the price of increased entropy production.
    But I have to take issue with the very last point you made, which is that we needed chaos to tell us that Newtonian dynamics could not produce super-strong analog computers. In fact, if you posit an infinitesimal but constant noise rate (like 10^-20), then analog computing pretty clearly fails, even without knowing anything about chaos. In other words, even if we had never heard of chaos, we’d be able to notice our inability to prove a threshold theorem for analog computing that could cope with i.i.d noise.
    What you propose is exactly one of the tests for classical and quantum chaos. If you add a bit of noise to a classical chaotic system you see that the entropy of the state grows linearly with time and the slope is practically independent on the noise magnitude. This slope is the Kolmogorov-Sinai entropy! The similar behavior is observed for many examples of quantum systems with chaotic classical counterparts but also for quantum systems with randomly chosen Hamiltonians (R.A. et.al PRL 77, 1996; J.Phys.A, 2007 and refs there). So, it is quite justified to say that this is a generic behavior.
    Again , a popular but completely wrong intuition is that quantum systems are intrinsically more stable than classical because the Schroedinger eq. is linear in contrast to the nonlinear Newton eq.
    
    Are superconductors chaotic? BECs? Lasers? And a classical RAM chip is still described by quantum mechanics: if it is chaotic, how does it store a bit so well?
    Firstly, few remarks about quantum states, macroscopic quantum states and classical states, a notoriously confusing issue. Notice, that all systems are quantum, only the states can be classified as above, “classical systems” is a short-hand term for quantum systems in classical states.
    Examples:
    1) One or few phonon state of macroscopic diamond is a quantum state , but not macroscopic quantum. One can entangle such states for two diamonds (realized experimentally), but one cannot “entangle diamonds”.
    2) A coherent state of 1000 phonons is a classical state.
    3) A superposition of such a state with another one with 2000 phonons is a macroscopic quantum state (never realized).
    4) Superconducting qubit states are quantum states, similarly to 1). They are superpositions of a ground state and a single-excited Cooper pair state (see arXiv:1012.0140, my previous preprints on this topic questioning a quantum character of Josephson qubits were wrong).
    5) Superconducting states of macroscopic samples and BEC states are classical states. The corresponding “condensate wave functions” are classical objects (e.g., they satisfy nonlinear Ginzburg-Landau or Gross-Pitaevski equations). They cannot be entangled (similarly to waves on Lake Ontario with waves on Lake Sniardwy ), and there are useless for QI/QC. Amazingly, there is PACS 03.75.Gg Entanglement and decoherence in Bose-Einstein condensates.
    
    Large superconductors, Lasers and BEC, which are classical, can display chaos in some range of parameters (some randomly found refs: Xu, et. al, Chaos in superconducting tunnel junctions, J.App.Phys.12, 1995; J.Ohtsubo, Semiconductor Lasers: Stability , Instability and Chaos, Springer 2010, K. Zhang, et.al, Hamiltonian chaos in a coupled BEC-optomechanical-cavity system, PRA 81, 2010). But those systems are also open systems operating in the classical regime. Environment not only selects classical states as the only relatively stable ones, but also adds friction to their dynamics. Friction can suppress chaos and “digitalizes” classical systems which can occupy discrete local minima of free energy separated from each other by macroscopic barriers. This is exactly the regime in which all classical computers operate. The price paid for stability is the work necessary to overcome friction which is dissipated into the system and makes classical gates irreversible. This does not harm classical computations, but I think, is deadly for quantum ones.
    
    Loading...
  - aram harrow permalink
    
    February 6, 2012 1:50 pm
    
    Craig, if you’ve found a flaw in the threshold theorem in the case of independent control errors, as you suggest, then you really should write it up!
    If correct, it’ll make a big splash.
    Here’s an example of a proof of the threshold theorem:
    http://arxiv.org/abs/quant-ph/0703264
    If it’s really wrong (and not just they missed a factor of 2, and so have to change the numerical value of the threshold), and you find something everyone has missed, then I promise your work will be very influential.
    
    Loading...
  - Craig permalink
    
    February 6, 2012 10:48 am
    
    Aram,
    
    The quantum error correcting codes papers are good mathematics, but don’t answer the following question:
    
    Quantum computing which factors integers works as follows: You have an initial state and you apply a polynomial number of unitary matrices to the initial state. In the real world, these unitary matrices each have an small error. But after a polynomial number of unitary matrices are multiplied together, this small error turns into a very large exponential size error.
    
    It’s just like copy machines making copies of copies of …. etc.
    
    Error correcting codes won’t help us here for the same reason why I observed when I was a kid that after 6 copies of a picture, the picture is no longer recognizable. The error correcting codes are part of the system. They don’t fundamentally improve the system, which is prone to error by definition.
    
    When I took a course in Numerical Linear Algebra, one of the biggest no-no’s I learned was multiplying matrices together when you don’t have to. Yet, this is the basis of quantum computing, not just once but many times!
    
    Loading...
  - John Sidles permalink
    
    February 6, 2012 11:46 am
    
    <Craig posts: “Error correcting codes are part of the system. They don’t fundamentally improve the system.”
    
    Craig, skeptics and nonskeptics alike appreciate that one of the greatest and most surprising discoveries of QC/QIT has been that this seemingly plausible assertion is not correct for a large class of quantum gate errors. Yet on the other hand, no error-correction method encompasses all classes of errors, and in this respect too QC skeptics and nonskeptics alike appreciate that John Preskill’s GLL post “Sufficient condition on noise correlations for scalable quantum computing” (with its attached notes and references) has been perhaps the single most outstanding contribution to this GLL discussion.
    
    For me, a one-sentence question describing a key open issue is: “Is Nature sufficiently ingenious and profligate in her noise-like dynamics, that neither she nor we need ever evolve dynamical trajectories on a covering Hilbert state-space of dimensionality sufficient for more-than-P computation?”
    
    At the present time, we don’t know enough even to be confident that this one-sentence question has a definite one-word answer (“yes” versus “no”) … it may well be that definitive answers await better-formed questions.
    
    This uncertainty is of course very good news for young researchers. 🙂
    
    Loading...
  - Craig permalink
    
    February 6, 2012 2:23 pm
    
    Aram,
    
    I never said I found any flaw in the threshold theorem. I said I found a flaw in the paradigm for quantum computing, as far as I understand it. How is it possible that you can multiply a bunch of n unitary matrices together, each having error epsilon without getting an exponential error of (1+epsilon)^n in the final matrix?
    
    I never said I was an expert in large scale quantum computing, but I know a silly theory when I hear it. And I think this explains why the theory is silly.
    
    Loading...
  - aram harrow permalink
    
    February 6, 2012 2:26 pm
    
    They’re unitary, so the error is at most n * epsilon.
    See Thm 2.2 of http://www.jstor.org/stable/55010 .
    
    Loading...
  - Craig permalink
    
    February 6, 2012 2:39 pm
    
    Thank you very much, aram.
    
    Well then in the words of the famous Gilda Radner, “Never mind!”
    
    Seriously, I appreciate you correcting me.
    
    Loading...
  - Craig permalink
    
    February 6, 2012 8:59 pm
    
    Thinking about this a little more, n*epsilon is still a large error, the order of n. Wouldn’t this still prohibit quantum computation for large n?
    
    Quantum error correcting codes still cannot help us here.
    
    Loading...
  - aram harrow permalink
    
    February 6, 2012 9:06 pm
    
    Yup, so you need FTQC to bring the per-gate error rate down to something like 1/10n. Using conventional proposals for this, the overhead is poly(log(n)), unfortunately with bad constants (like millions or billions).
    
    Loading...
  - Craig permalink
    
    February 6, 2012 9:42 pm
    
    Thank you aram,
    
    Now, I see that this why this is a difficult problem.
    
    I cannot prove this, but I think that large-scale quantum computers will not work because we live in a digital universe with a limited amount of memory space. Large-scale quantum computers will generate an overflow error.
    
    This is the only explanation I can see why scalable quantum computers won’t work. I just cannot believe that we live in a universe where it is possible to factor integers easily but impossible to solve NP-hard problems easily.
    
    Loading...
  - Craig permalink
    
    February 9, 2012 6:58 pm
    
    It looks like I was right when I said, “That’s like offering $100,000 to anyone who can prove that Bigfoot doesn’t exist.”
    
    Look at comment #97 here by Scott:
    http://www.scottaaronson.com/blog/?p=902#comments
    
    “Drew #95:”Your” money is in my bank account, retirement fund, etc. 🙂 , and it’ll stay there until someone offers a reason why quantum computing is impossible in principle—meaning, not in my lifetime, not in the next hundred years, but forever.”
    
    This was a response to comment #95, that proposed a solution to Scott’s problem.
    
    Unless I’m misunderstanding this statement, this offer of $100K appears to be just a publicity stunt.
    
    Loading...
- Gil Kalai permalink
  
  February 2, 2012 1:49 pm
  
  “In response to Boaz’s extremely-pertinent question, of whether, if FTQC is impossible, that means there’s an efficient classical simulation of realistic quantum systems (and if so, what is it?), Gil basically says that he doesn’t know”
  
  Hi Scott,
  
  I said (in response to my understanding of Boaz’s question) that I dont know if imposing Conjectures 1-4 on a model for noisy quantum computers suffices to reduce their power to BPP. (I also said that while I cannot give a complete answer, I know something about this question, it is related to interesting questions in computational complexity, my papers discuss them, and I will relate to them a bit later.)
  
  A related question is if there are other ways to get a speed up over BPP even if fault tolerance quantum computer based on error correcting codes is impossible. It is also interesting. (We need to find the right formal way to say “quantum fault tolerance based on error correcting codes is impossible.” You can regard my approach as trying to say this formally)
  
  Another question is: if computationally superior quantum computation is impossible, and thus BPP is the compleity class describing decision languages that nature can answer, does this mean that that there is an efficient classical simulation of realistic quantum systems? And if the answer is yes, can I kindly describe how these classical simulation goes.
  
  This is an interesting question (although we need to work a little to put it on formal ground). It was amply discussed on your blog, and I even participated. We may come to this question later.
  
  I must admit that I don’t now to describe how to simulate even physical processes for which we do expect simulation with classical computers exist, and also that it is quite a hard work, which in many cases remains to be done, to describe how to simulate realistic quantum systems with quantum computers. So, overall, I do not understand your complaints.
  
  “who can say what the complexity of simulating physics really is? Maybe it’s more than BQP. Maybe it’s less than BQP. Maybe it’s incomparable.” Note that strictly speaking, all three possibilities are perfectly consistent with QM (e.g., maybe there are powerful oracle unitaries available, or gigantic Hilbert spaces). What’s strange to me is focussing on one of these possibilities over the others.
  
  In this discussion we focus on quantum error correction and not so much on computational complexity. This may seem strange to you but in my view there are good reasons for that. The computational complexity questions are very interesting as well. We may discuss them as well. Again, I dont undersnad what is your complaint.
  
  Your 100,000$ pledge is very generous and nice.
  
  Loading...
  
  Reply
  - Craig permalink
    
    February 2, 2012 5:57 pm
    
    Gil,
    
    The following is in no way intended to be a criticism against Scott, just a general comment:
    
    Pledging money is not generous and nice. It’s the following through on a pledge that is generous and nice. See Genesis בְּרֵאשִׁית 23.
    
    Loading...
John Sidles permalink

February 2, 2012 10:54 am

A hugely enjoyable aspect of this debate are the opportunities it affords us for quoting inspiring passages, citing seminal articles … and especially, telling funny stories.

For inspiration it’s hard to beat Scott’s post (above), which which the following inspiring passage appears (here lightly universalized):

“There’s a detailed picture of [what] the world could be like such that QC is possible, but no serious competing picture of what the world could be like such that it isn’t. That situation could change at any time, and we would welcome it as the scientific adventure of our lives.”

What is a suitable starting point (for students especially) to embark upon this adventure? Everyone has their own ideas, and so let me commend one possible starting point (of many) that is the focus of two recent arxiv articles: Sarovar and Milburn’s Continuous quantum error correction (arXiv:quant-ph/0501049) and Oreshkov and Brun’s Continuous quantum error correction for non-Markovian decoherence (arXiv:0705.2342).

How might these ideas in these articles be further developed? For inspiration we can turn to ergodic theory in general and the Kolmogorov-Arnold-Moser (KAM) Theorem in particular. This particular research roadmap is inspired by the following parallels between ergodic theory and FTQC. For many centuries it was postulated that (save for a set of measure zero) Hamiltonian dynamical systems generically were ergodic; similarly for several decades it was widely expected that quantum noise destroys any realistic possibility of QC. However, beginning in the 1950s numerical experiments (very unexpectedly) observed quasi-stable trajectories for a special class of Hamiltonian dynamical systems; similarly for a special class of noise mechanisms, the unexpected existence of error-correction methods has been demonstrated.

The great achievement of KAM theory was to prove quasi-stability rigorously and generally. It is natural to wonder whether a similarly rigorous KAM-type theory might exist for (continuous) FTQC. Specifically, if we translate the continuous error-correction dynamics of Sarovar, Milburn, Oreshkov, and Brun (and many others) into the symplectic language of KAM theory, can we rigorously prove (or disprove) the existence of continuous error-correcting quantum dynamics upon computational manifolds having dimensionality sufficiently great for universal quantum computation?

There are plausible arguments for-and-against such a “quantum super-KAM theorem.” A plausible argument “for” is the promising numerical results of Sarovar, Milburn, Oreshkov, and Brun (etc.). A plausible argument “against” is (what I take to be) a geometrized version of the arguments of Geordie Rose and Gil Kalai, that we should expect quantum super-KAM mechanisms to fail generically in QC, because the dimensionality of the computational space increases exponentially while the dimensionality of the error-correcting generators increases only polynomially.

Like anyone who works problems associated to these issues, I have my own set of experiences and ideas relating to the various obstructions (both numerical and theoretical) to proving / disproving quantum super-KAM theorems — obstructions that are generically associated to the historically tough issues of spatial localization, renormalization, and causality (topics for which quantum field theory in particular exhibits various interlocking pathologies). But a broader and more universal observation is that nowadays the math-and-physics tools required to “get started” in quantum super-KAM research are sufficiently simple as to be exhibited to students on one page, and yet this post-Dirac theoretical toolset is sufficiently deep and broad as to amply provision 21st century students for what Scott aptly calls “the scientific adventure of our lives.” Which is all good! 🙂

As for a funny story, here’s one that Ingo Müller tells about his thesis advisor, the prominent thermodynamicist Clifford Truesdell, who fought an lifelong (and ultimately losing) battle against what he regarded as the heresy of “Onsagerism” (so perhaps Geordie Rose especially will appreciate this story):

Truesdell was a consummate theoretician. He showed nothing but disdain for experiments, be they conducted in the laboratory or on the computer.

So, when Truesdell visited me in Berlin, on the first day he came and said “Ingo, can I ask you for a favour?” And I, eager to please my visitor and one-time mentor, said “Of course, Clifford. What can I do for you?”

Truesdell: “Please don’t show me your lab.”

So by the end of the 21st century, will FTQC be regarded as gospel or heresy? Or might it be regarded (per Truesdell) as theoretical gospel and experimental heresy. Right now, no-one knows … and for sure, we will have plenty of fun finding out, both in our equations and in our laboratories. 🙂

Loading...

Reply
rrtucci permalink

February 2, 2012 12:16 pm

Is Aram, the other “debater”, writing a dissertation in Greek, as a reply?

Loading...

Reply
- aram permalink
  
  February 5, 2012 8:24 pm
  
  Ah, internet time…
  
  Loading...
  
  Reply
Gil Kalai permalink

February 2, 2012 2:09 pm

Dear all, let me make one comment on Aram’s short response, (it is related to computational complexity issues)

Aram wrote: “Conversely, Gil’s skepticism is based on error models that may have low single-qubit error rates, but are highly correlated even across large distances.”

This is true, but there is more to it. When we have “bad noise”(or detrimental noise as I call it) that obeys conjecture 1, (or conjectures 2 or 3) there can be a very large discrepancy between “single qubit error-rate” and between error rate in terms of trace distance (of the joint state of all qubits) per a (small) time unit. The trace-distance rate seems the correct and relevant measure. As a result, conjectures 1, 2, and 3 suggest that for highly entangled states the single qubit error-rate itself will scale up with the number of qubits. This will be the most devastating aspect of correlated errors.

Loading...

Reply
Gil Kalai permalink

February 3, 2012 4:20 pm

A computational complexity question

I gave a longish respond to Boaz regarding computational complexity issues. It occurs to me that there is a potentially very nice problem that we can try to ask.

Consider the Conjecture 1. It says that we cannot create (essentially) a noiseless qubit, where by “qubit” we refer not just to “raw” qubits of our quantum computer but also to “protected” qubits created on some sub Hilbert space. (Note that in nature we cannot single out what the “raw qubits” are.)

Suppose we make only this noisy qubits assumption assumption:

All qubits defined by our quantum computer are (substantially) noisy.

What will be the remaining computational power? Will such assumption be enough to push down the computational problem to BPP? The question is not fully formal but it look to me that it can be formalized. It seems interesting regardless of quantum computer skepticism.

Actually, Scott asked in his early youth about what he called Shur/Shor separators: quantum states that if we cannot reach them we cannot factor. This would not be a Shur/Shor seperator in the strict Scott’s sense, but it will have the same spirit.

Loading...

Reply
John Sidles permalink

February 3, 2012 5:06 pm

Gil postulates: “All qubits defined by our quantum computer are (substantially) noisy.”

Even in clinical medicine, techniques that (substantially) protect quantum order from noise are routinely practiced (for example, Vasos et al. “Storage of nuclear magnetization as long-lived singlet order in low magnetic field” (2010)). So this GLL discussion is partly about whether these eminently practicable — even clinical — coherence protection techniques can be scaled (both in fundamental physical principle and in feasible engineering practice) to extremely high orders of coherence sustained throughout intricate computational dynamics.

Seemingly, this is another case in which the boundaries between between (impossible) $\Leftrightarrow$ (infeasible) $\Leftrightarrow$ (practicable) are less mathematically and physically natural than we would like.

Loading...

Reply
- Gil Kalai permalink
  
  February 3, 2012 6:12 pm
  
  Dear John
  
  “Substantial” here is in the computer science sense, namely greater than a constant say 10^-9.
  
  QEC allows creating manipulable qubits with error going to 0 as the number of qubits used in the encoding increase. The computational complexity question is if imposing at least epsilon noise on every quibit (raw or encoded) reduce the computational power to BPP.
  
  Loading...
  
  Reply
Boaz Barak permalink

February 3, 2012 9:05 pm

Thank you Gil for the response. I guess in a blog, especially in a comment, it’s hard to make things fully formal so I can’t say I fully understand this “noisy qubit assumption” (I guess because I’m not completely sure what are raw vs protected qubits ). Still, I think I get the larger picture.

It seems that perhaps several issues are conflated together. There is the big question whether quantum mechanics can allow any kind of super polynomial speed up above classical computation, the next question whether it allows to build a device capturing the full power of BQP, and the third question whether that device can be built by performing a gate by gate computation combined with quantum error correction codes. Your conjectures are first and foremost about the last question, though it may be that if true, they end up answering the second and first one. is that a correct understanding?

What’s somewhat still confuses me is the following. You could have simply conjectured that for some fundamental reason, the noise rate will always stay above, say, 45% or whatever the number is for the threshold theorem to fail. But you seem to assume that it would be physically possible to reduce the expected number of errors to an arbitrarily low amount, but somehow correlation will stay high. If indeed it would be possible to reduce the noise to an arbitrary low level epsilon by spending f(epsilon) resources, do you have a conjecture what f(epsilon) is? In particular, by your comment that log depth suffices for factoring, does it mean that even if f is exponential in 1/epsilon then we could still factor n bit numbers with poly(n) resources?

Loading...

Reply
- Robert Alicki permalink
  
  February 4, 2012 4:44 am
  
  Dear All,
  although you consistenly ignore all arguments based on physics let me try again.
  Why the threshold theorems MUST be meaningless for real physical systems ?
  Because, as the crucial parameter they use error/per gate which in all physical models is proportional to the square of the COUPLING!!! to environment. On the other hand the only known protection mechanism, valid for classical models as well for quantum ones (topological models) depends on the TEMPERATURE!!!
  Consider a piece of ferromagnet which encodes a bit in its magnetization (up or down). You can reduce the coupling to environment million or billion times, but as long as the temperature is above the critical Curie one, spontaneous magnetization dissapears and the encoded information is lost. The same is true for quantum topological models (e.g. 4D Kitaev model). So, not the strength of the coupling is relevant but the ratio between processes increasing and decreasing energy which is given by the Boltzmann factor
  \exp{- E/kT}.
  Obviously, coupling cannot be too large to avoid all “dressing” processes which could transform computer’s qubits into complicated “polarons” containing some environment’s degrees of freedom.
  
  Loading...
  
  Reply
  - Joe Fitzsimons permalink
    
    February 4, 2012 9:11 am
    
    Dear Robert,
    
    As a fellow physicist I must take issue with some of the claims in comment. First of all, as you must be aware, most implementations of quantum computing use systems which are far from thermal equilibrium with the environment (sometimes even internally). The role of fault-tolerance is to keep them from thermalising. The coupling to the environment is crucial, since this is what governs the time scale for thermalisation. The error correction is extending the thermalisation timescale to be significantly longer than the computation. You seem to totally neglect this.
    
    The statement that topological models are the only known protection mechanism for both classical and quantum computation is clearly false. You also seem to be implying that topological fault-tolerance is necessarily only passive error correction (by way of the claimed dependence only on temperature dependence), but this is somewhat misleading as there are active schemes for error-correction and fault-tolerance based on topological codes.
    
    Lastly, the talk of a critical temperature for passive correction is not an objection to fault-tolerant quantum computation, but rather seems to be an admission that it is possible. The existence of a critical temperature for passive schemes is analogous to the error threshold in active correction. One expects a phase transition!
    
    Loading...
  - Joe Fitzsimons permalink
    
    February 4, 2012 9:18 am
    
    Let me also quickly add that if all quantum systems thermalised in sub-exponential time (in the size of the system), then we would have a way to solve a much stronger class of problems efficiently with physical systems: Finding ground states of local Hamiltonians is QMA-complete, and even finding ground states for the Ising model (no transverse field or anything messy) is NP-complete. Indeed, the adiabatic model *tries* to reach thermal states of a target Hamiltonian quickly.
    
    Loading...
  - Robert Alicki permalink
    
    February 4, 2012 10:55 am
    
    Dear Joe,
    thank you very much, finally something about physics and not only abstract structures derived from complexity theory.
    
    1) “if all quantum systems thermalised in sub-exponential time (in the size of the system), then we would have a way to solve a much stronger class of problems efficiently with physical systems. Finding ground states of local Hamiltonians is QMA-complete,”
    
    Firstly, systems thermalize to finite temperature states and not to ground states (III -law of thermodynamics). To get a ground state you need not only fast relaxation but also fast cooling forbiden by thermodynamics.
    Secondly, even if you have a ground state then its measurement in computational basis is a problem. You do not have FT-measurements, for sure, not for observables which do not commute with the Hamiltonian. Measurements errors cumulate and give exponentially small (in size) probability of the right answer.
    
    2) “The statement that topological models are the only known protection mechanism for both classical and quantum computation is clearly false”
    
    Not topological, of course, I use examples of quantum topological models , because they are simple enough to be rigorously analyzed. However, the mechanism based on free energy bariers , growing with the size of the system, between the states encoding information seems to be universal. Please, show me a single example of other mechanisms proved to work?
    
    3) The difference between active and passive protection is not so big as one can think. Imagine a circuit model with all the QEC machinery working simply as a memory. Then it should be equivalent to an open quantum system driven by periodic Hamiltonian (error correction rounds). Such systems are very similar to systems with constant Hamiltonians (see my paper with Daniel Lidar and Paulo Zanardi, Phys. Rev. A 73, 052311 (2006)) and therefore, the mechanisms of protection should be essentially the same.
    
    4) The fact that the systems are far from equilibrium does not help, the laws of thermodynamics must be obeyed, in particular entropy production must be positive .
    Probability of deviations from this principle decreases exponentially with the size of a system x time (“fluctuation theorems”) and hence also does not help. One should remember that information is not destroyed only by large entropy, which can be removed from the system by cooling, but by the always non-negative entropy production. The later is minus x change of relative entropy (relative entropy is a measure of state distinguishability). In a non-equilibrium environment (e.g. many baths with different temperatures) the entropy production is larger than in an equilibrium one (single heat bath) due to transport processes.
    
    Loading...
- Gil Kalai permalink
  
  February 4, 2012 10:09 pm
  
  Your conjectures are first and foremost about the last question, though it may be that if true, they end up answering the second and first one. is that a correct understanding?
  
  Dear Boaz, yes this is correct. But note that the question about quantum codes extends beyond the gate/qubit model and also note that the proposed conjectures are not asymptotic, unlike your three formulations. Let me come back to the other interesting question you raised later. (Probably next week end).
  
  Loading...
  
  Reply
John Preskill permalink

February 4, 2012 11:22 am

I hope Robert Alicki realizes that I have always taken his criticism seriously. In particular, my paper with Ng proving a quantum accuracy threshold theorem for a system coupled to an oscillator bath at nonzero temperature [Phys. Rev. A 79, 032318 (2009)] was partly motivated by one of Alicki’s objections to previously known threshold theorems.

I have also found Gil Kalai’s skepticism stimulating, and I enjoyed our discussions during Gil’s visit to Caltech last year. Gil’s visit provided the impetus for me to work out some sufficient conditions for scalable quantum computing, something I had been meaning to do anyway. The results are a bit much to explain in a blog post, but I have posted my notes at
http://www.theory.caltech.edu/~preskill/papers/correlated-error-v1.pdf
for those who want to see more details.

Gil says that while he is skeptical of quantum computing he is not skeptical of quantum mechanics. Therefore, I presume he takes for granted that a quantum computer (the “system”) and its environment (the “bath”) can be described by some Hamiltonian, and that the joint evolution of the system and bath is determined by solving the time-dependent Schroedinger equation. If Gil’s conjectures are true, then, no matter how we engineer the system, the Hamiltonian and/or the initial quantum state of the joint system must impose noise correlations that overwhelm fault-tolerant quantum protocols as the system scales up.

In this setting, it is interesting to ask what conditions on the initial state and on the Hamiltonian suffice for scalable large scale quantum computing. The main result in my notes is the proof of a theorem that establishes such a condition. Actually, it extends to a more general setting a result proved in a paper with Aharonov and Kitaev [Phys. Rev. Lett. 96, 050504].

As others have suggested in their comments, the key is that noise acting collectively on many qubits simultaneously should be adequately suppressed. I consider a Hamiltonian coupling the system to the bath, which includes terms acting collectively on many system qubits. Loosely speaking, the sufficient condition is that the terms in the Hamiltonian that act on k system qubits have an operator norm that decays exponentially with k, and that for each fixed k, the operator norm decays quickly enough as the qubits separate in space. Under these conditions, correlations in the noise are weak enough for fault-tolerant quantum computing to succeed.

Of course, I do not mean to suggest that these conditions are necessary. Part of the point of the paper with Ng cited above is that we can still prove a threshold theorem in cases where the these norm conditions on the Hamiltonian are violated, by making additional assumptions about the initial state of the bath. In the theorem proved there, it is a Gaussian (e.g. thermal) state, with spatial correlations that decay quickly enough.

In any case, Gil believes that Hamiltonian noise models like the one discussed in my notes are not physically realizable; that could well be, though I would like to understand better his reasons for holding that opinion. And it is a big leap from there to the statement that large-scale quantum computing is impossible.

Skepticism about the feasibility of fault-tolerant quantum computing is reasonable, and welcome; it raises the stakes as the scientific/engineering community strives to extend the reach of quantum computing. Gil’s conjectures also highlight the importance of attaining firm experimental evidence for quasiparticles obeying nonabelian statistics in laboratory systems, since quantum states supporting anyons are highly entangled many-particle states similar to the code states of quantum error-correcting codes.

Since I just typed up my (sloppy) handwritten notes yesterday, the typed notes may contain errors and obscurities. I would welcome comments, questions, corrections, and criticisms, though I may ignore them anyway. (This is my foray into Open Science, in homage to Michael Nielsen.)

Loading...

Reply
- Cristopher Moore permalink
  
  February 5, 2012 11:48 am
  
  I agree that the issues of correlated noise are subtle and important, and I’m glad that Jon and his collaborators are addressing them — although I see no particular motivation for the conjecture that these correlations conspire to prevent large-scale QC, as per my snarky comparison with heavier-than-air flight, which Wim van Dam independently thought of on the Pontiff.
  
  But Gil, your conjectured limit on entanglement (conjecture C) does seem to me to be inconsistent with QM. I am also confused by the fact that some of your conjectures are phrased as “for any (noisy) quantum computer…” What’s a “noisy quantum computer”? You don’t mean a circuit of polynomial size with the usual model of gate and phase errors, since then we would already know it to be false.
  
  So what class of physical processes constitute noisy QCs in your definition? How do they differ from a general physical systems, which you agree are governed by QM, and which certainly can become highly entangled? You refer to processes that do or do not “enact fault-tolerance”, but that is just a physical process like any other. So I still don’t understand what your conjectures really mean physically, or whether they are well-defined.
  
  Loading...
  
  Reply
  - Gil Kalai permalink
    
    February 9, 2012 6:31 am
    
    “But Gil, your conjectured limit on entanglement (conjecture C) does seem to me to be inconsistent with QM.”
    
    Ok lets think about it together. What is the difference between
    
    (*) A state with very high entanglement (according to the measure I use)cannot be created or approximated by a (realistic model) of a noisy quantum computer)
    
    (**) A state which represent a random unitary operator on n qubits cannot be created or approximated by a (realistic model) of a noisy quantum computer.
    
    I think neither (*) nor (**) viaolate QM.
    
    (Regarding your example, the entanglement measure I use should give something linear or quadratic in n but tell me the precise state you refer to and I will double check.)
    
    Loading...
- Cristopher Moore permalink
  
  February 5, 2012 11:55 am
  
  Gil, looking again at conjecture C, why can’t I have a bundle of n fiber-optic cables, and send half of a pair of entangled photons down each one? Doesn’t this already give (close to) a maximally-entangled state on n qubits, violating your conjecture? And isn’t this already feasible with current technology? You can say that photons are hard to store, but then I can use a Bose-Einstein condensate, etc. etc… What am I missing?
  
  Loading...
  
  Reply
  - John Sidles permalink
    
    February 5, 2012 12:57 pm
    
    Chris, from both a fundamental math-and-physics point-of-view, and from a practical quantum systems engineering point-of-view, the following superficially similar propositions are in fact very different:
    
    Case 1: launch entangled photons into low-efficiency detectors, versus
    
    Case 2: launch entangled photons into high-efficiency detectors.
    
    In the context of Case 1, it is an excellent approximation to regard the photon-source currents as physically and informatically independent of the photon-detector currents. This hugely simplifies the subsequent analysis, which is why the celebrated Feynman Lectures (to cite one textbook of many) embrace the approximation of source-sink independence implicitly.
    
    But in the Case 2 limit of near-perfect detector efficiency, the photon-source currents are (of course) correlated nearly perfectly with photon-detector currents (via Schwinger-style Maxwell field equations, naturally) — wholly contrary to the physical intuitions that the Feynman Lectures (again as one textbook of many) encourage students to cultivate.
    
    The physical regime of strong source-sink correlations (aka cavity electrodynamics) dominates the physics of (to cite just example) Aaronson-Arkhipov experiments for computing the permanent. And here there is no substitute for grappling head-on with exceedingly difficult field-theoretic issues associated to spatial localization, renormalization, and causality (as Robert Alicki’s GLL posts already have been rightly emphasizing).
    
    Needless to say, it is precisely in these same areas of spatial localization, renormalization, and informatic causality that standard QM encounters significant difficulties (and even outright pathologies). The point being, that for better or worse (definitely better IMHO), the research strategy of focusing one’s attention upon QC/QIT offers no refuge from these still-unmet fundamental challenges in mathematics and physics … if anything, these fundamental challenges are sharpened … which is good. 🙂
    
    Elevator Summary Math-and-physics students in particular should be aware of a Great Truth of QM/QC/QIT, that overmuch regard for the simplified intuitions of even the respected textbooks (the Feynman Lectures in particular) can subtly yet needlessly ensnare one’s physical and mathematical investigations in a disheartening Groundhog Day.
    
    Loading...
John Sidles permalink

February 4, 2012 1:36 pm

John Preskill notes: “It is interesting to ask what conditions on the initial state and on the Hamiltonian suffice for scalable large scale quantum computing.”

John, I hope you don’t mind “fan mail” for both your articles and for your outstanding on-line lecture notes, which are deserving of appreciation and thanks similarly to the work of many other GLL posters. Yet isn’t it both mathematically natural and physically illuminating to add to your list “conditions on the state-space geometry.”

Speaking as one of the increasing cohort 21st century STEM professionals who are increasingly (to borrow a phrase from Samuel Clemens) “filled with the easy confidence that geometry inspires,” it may perhaps be that case that a narrow focus upon QC as a mainly algebraic discipline that is exclusively concerned with initial conditions, Hamiltonians, and POVMs, comprises a mathematical point-of-view that is sufficiently restrictive — yet unnecessarily restrictive — as to afford little opportunity (for young researchers in particular) to escape our collective “QC Groundhog Day.”

Loading...

Reply
Roger permalink

February 5, 2012 12:49 pm

No, the burden is not on the QC skeptics. The AC advocates are claiming something that has never been observed, and that is contrary to longstanding understandings about how the world works. The burden is on the QC advocates.

Loading...

Reply
- Scott Aaronson permalink
  
  February 5, 2012 2:09 pm
  
  No, if you accept quantum mechanics, the burden is on you to explain why a computer couldn’t be built that takes advantage of the phenomena of superposition, interference, and entanglement that have been the entire core of quantum mechanics, verified over and over, since 1926.
  
  Believing quantum mechanics but not accepting the possibility of QC is somewhat like believing Newtonian physics but not accepting the possibility of humans traveling to Mars. (“Sure, they’ve gone to the moon, but Mars? That’s just nutty! It’s never been observed, and is contrary to longstanding understandings about where human beings live.”) You might (or might not) feel blithely secure that your position won’t be empirically challenged for some time. But if you’re not at least troubled by the tension and thinking about how to resolve it (as Gil is), then your position is already as feeble as can possibly be.
  
  What is it about the laws of physics that prevents humans from going on Mars? What would go wrong if you tried to send someone there? What is it that could possibly explain why humans can go to the Moon, but not Mars? We don’t literally have to send someone to Mars before we can ask these questions! And the burden is on you to answer them. Take your time…
  
  Loading...
  
  Reply
  - Robert Alicki permalink
    
    February 5, 2012 3:54 pm
    
    Obviously the burden is on those, who presents such extraordinary claims like :” the larger is the system the more efficiently one can beat decoherence ”
    In the present “publish or perish” era only very few and rather older guys, like Gil (sorry!) and me, can and want to spend some time searching for holes in the proposed designs of FTQC as our predecessors did with proposals of perpetuum mobile 2 centuries ago.
    
    The analogy to space travel is not appropriate. The right question is
    
    What is it about the laws of physics that prevents spontaneous creation of Boeing 747 on a scrap-heap?
    
    Loading...
  - Scott Aaronson permalink
    
    February 6, 2012 12:08 am
    
    Robert, I see no reason whatsoever why a QC should be considered as a priori implausible as a 747 being assembled in a scrap-heap. While your previous comments revealed nothing but contempt for complexity theory, this really is largely a complexity issue: if, for example, QCs would solve NP-complete problems or the halting problem in linear time, then I might also suspect that something as-yet unknown about physics “must” prevent them from working (though even then, I wouldn’t share your certainty). But factoring? Solving Pell’s equation? The idea that elegant uses of quantum interference would let you nab those special number-theoretic problems, but NOT NP-complete problems, is weird enough to be true.
    
    Loading...
  - Michał Kotowski permalink
    
    February 6, 2012 10:58 am
    
    “While your previous comments revealed nothing but contempt for complexity theory, this really is largely a complexity issue:”
    
    Scott, I think you’re going too far here – why the complexity theory perspective is surely relevant and Robert Alicki’s somewhat bitter tone is a little puzzling, I think he made it clear enough that in his view the issue with quantum fault tolerance is of *thermodynamical* nature and concerns the error models used to prove threshold theorems. Simply saying that BQP is unlikely to be very powerful so QC doesn’t look completely implausible doesn’t address any of the physical issues Alicki raised.
    
    Loading...
- Roger permalink
  
  February 5, 2012 11:01 pm
  
  I accept quantum mechanics, but not quantum computing. It is just not true that quantum computing follows from the quantum mechanics of 1926. I guess you tried to show that in your paper and failed. So you claim that somehow the burden is on someone else to show the opposite.
  
  The Mars analogy is ridiculous. The feasibility of a Mars trip is an easy extrapolation from the Moon trip. But there is no demonstrated feasibility of quantum computing.
  
  Loading...
  
  Reply
  - Scott Aaronson permalink
    
    February 6, 2012 12:30 am
    
    You obviously didn’t read my paper and have no idea what’s in it. I did exactly the opposite of what you say there: I tried and failed to substantiate the skeptical position, by finding some sort of criterion that would separate the quantum states that are already confirmed experimentally from the ones needed for Shor’s algorithm. If such a separating criterion existed, it of course would immediately suggest something for the experimentalists to try: namely, see whether or not Nature respects that criterion! On the other hand, if no such separating criterion exists, then my Moon vs. Mars analogy is a perfectly valid one.
    
    So, can you propose such a separating criterion? If not, then does your inability to explain where the extrapolation from 1926 quantum mechanics to Shor’s algorithm breaks down bother or trouble you in the least?
    
    Loading...
  - Roger permalink
    
    February 6, 2012 1:02 am
    
    Scott, you couldn’t prove what you wanted to prove, but you claimed that you were right anyway because you could not prove the opposite. Gil has proposed hypotheses that separate quantum mechanics from quantum computing. You just don’t accept them.
    
    QC has not gotten to the Moon and is just waiting for Mars funding. QC has not gotten off the ground. It just seems like a lot of wishful thinking to me. I don’t see any evidence for it.
    
    Loading...
  - Scott Aaronson permalink
    
    February 6, 2012 7:43 am
    
    “Gil has proposed hypotheses that separate quantum mechanics from quantum computing.”
    
    That’s the first thing you’ve said in this entire discussion that hints at what you might actually believe! So then, do you agree with Gil’s hypotheses? Or with some of them but not others?
    
    You’ll notice that Gil calls his hypotheses “conjectures”: not only can he adduce little evidence for them (not surprisingly, given the strangeness of the error models they would require), they’re not precisely stated, and even if they held in some form, it’s far from clear whether or not they would actually kill QC! If you read Gil’s paper, he’s honest enough to admit that many of his conjectures seem “merely” to reduce QC to logarithmic-depth—i.e., still enough to implement Shor’s factoring algorithm!
    
    The point of my paper was to explain why separating quantum mechanics from quantum computing is such a hard problem. I’ve said many times that if someone solves that problem, it’ll be the scientific thrill of my life (and I even accepted Gil’s challenge to put money behind that statement). Certainly, it would be much more exciting than the “mere” building of a quantum computer, since it would require overturning so much of what scientists (and not just QC researchers, but chemists, nuclear physicists, high-energy physicists, etc., few of whom think there’s any problem of principle with QC) currently believe about the way quantum mechanics works.
    
    I agree with you that in my analogy, QC hasn’t yet gotten to the moon. I’d say it’s still in the stage of shooting model rockets into the air — i.e., maybe the 1920s or so. Then, as now, you had skeptics loudly proclaiming the impossibility of the goal—yet while those skeptics considered themselves “conservatives,” they were really radicals, in that (without, of course, ever admitting it) they rejected what was already understood about the laws of physics. In that case, the time to vindication of the “conservative” viewpoint was ~40 years.
    
    Loading...
  - John Sidles permalink
    
    February 6, 2012 9:17 am
    
    Scott asserts: “Not just QC researchers, but chemists, nuclear physicists, high-energy physicists, etc., few of whom think there’s any problem of principle with QC.”
    
    The complement of the preceding Great Truth is something like:
    
    Scarcely any chemists, nuclear physicists, high-energy physicists, etc., believe there are no problems of principle with QC.”
    
    And this too would be a Great Truth, both in a pragmatic yet important sense (chemists and nuclear physicists seldom compute on linear state-spaces, for the practical reason that there is little need to do so) and also in a fundamental sense (the struggle to unify relativity with QM has convinced many fundamental physics researchers that both theories are incomplete).
    
    So will we humans ever create practicable computational technologies that require exponential-dimension Hilbert spaces for their accurate operation? That is one of the key points being discussed here on GLL … and it is still at-issue.
    
    And on that happy day — be it soon or be it distant — that we humans create new theoretical frameworks that unify principles of relativity and QM, will exponential-dimension QC-supporting Hilbert spaces be part of that description? That too is one of the key points being discussed here on GLL … and it too is still at-issue.
    
    With diverse Great Truths being preached, and numerous practical and fundamental problems increasingly appreciated as being wide open, it’s becoming a terrific era to conceive novel mathematical tools, conduct ground-breaking scientific research, and launch transformational enterprises in QM / QC / QIT. 🙂
    
    Loading...
  - Roger permalink
    
    February 7, 2012 5:56 pm
    
    Scott says that understanding the impossibility of quantum computing is a hard problem. To me it seems easy. QC is implausible and there is no evidence for it.
    
    Loading...
  - Scott Aaronson permalink
    
    February 7, 2012 8:49 pm
    
    ROTFL! Sure, it’s easy to understand the impossibility of quantum computing, in exactly the same way it’s easy to understand how the earth can be resting on a giant turtle. The key is not to ask what the turtle’s standing on, and likewise, not to ask what the flaw is in our current understanding of quantum mechanics that makes QC impossible. All sorts of scientific problems can be quickly cleared up this way, once we learn to stop asking annoying followup questions and embrace doofosity!
    
    Loading...
  - Craig permalink
    
    February 7, 2012 10:05 pm
    
    Scott,
    
    Comparing the impossibility of quantum computing to the earth resting on a turtle is a bad analogy: No large scale QC machine has ever been built. And no turtle holding up the earth has ever been found. So it’s more natural to compare the possibility of quantum computing to the earth resting on a turtle.
    
    I said before I’m not an expert but a skeptic. I have a question. Let’s look at Grover’s algorithm. The precision required at each step for the entries of the unitary matrix is epsilon=1/2^{n/2}. In the real world, how is it possible to get this precision?
    
    I hope you realize that this is not the same thing as 10K photons polarized at 45 degrees, as you talk about in your paper. In this example, the 1/2^{n/2} is just something you need for normalization. In the Grover’s algorithm example, the 1/2^{n/2} is more than this.
    
    Loading...
  - aram harrow permalink
    
    February 7, 2012 10:09 pm
    
    You don’t need this much precision. If you approximate the whole matrix to operator-norm error 0.1 then it’ll work fine.
    
    Loading...
  - Roger permalink
    
    February 7, 2012 10:11 pm
    
    Craig is right. Scott is the one with goofy turtle proposal. I accept all of the known science, and QC is the wildly speculative proposal. Scott, your position is like asking for proof that time travel is impossible.
    
    Loading...
  - Craig permalink
    
    February 7, 2012 10:12 pm
    
    Thanks aram,
    
    Wow. That’s a surprise.
    
    Loading...
  - Craig permalink
    
    February 7, 2012 10:16 pm
    
    aram,
    
    I assume that this is the same for Shor’s algorithm. If this is the case, then perhaps it is possible to adjust Shor’s algorithm so that you could factor in polynomial time on a classical computer? Somehow I don’t believe this, but I’m curious what is preventing someone from doing this?
    
    Loading...
  - aram harrow permalink
    
    February 7, 2012 10:20 pm
    
    I don’t know what you proposed modification is, but if you try it, you might be able to see what goes wrong. Or it’ll work, and that’ll be great too.
    
    Loading...
  - Craig permalink
    
    February 7, 2012 10:34 pm
    
    aram,
    
    I don’t have any proposed modification. It’s just that if you have a large matrix of entries with not much precision relative to the size of the matrix, my intuition tells me that you should be able to dramatically reduce the size of the matrix and get a similar result.
    
    But then again, the final state must be an exponential size vector to be meaningful, so perhaps not.
    
    Loading...
  - Lewis Mammel permalink
    
    March 5, 2012 1:02 am
    
    I agree with you. We are in the realm here of rhetoric and semiotics it seems to me. The physics I learned in grad school ( Ph.D. 1979 ) just isn’t connecting to the QC concept. And how is a 3 GHz processor a “classical” device? All the engineering is based on quantum physics of the solid state. We have quantum computers, and indeed it’s a quantum world. How about the zero phonon line? That’s “quantum entanglement” of the entire crystal. It happens routinely. The QC is part of the trend started by the Aspect experiment – “parlor trick” physics, as I think of it. That is, experiments to tease out and illustrate the intuitive extremes of QM implications. The sodium doublet just isn’t good enough for some people.
    
    But when we come to the point of engineering the terms in a configuration interaction molecule oribital calculation, I lose track. I’m just not seeing anything that explains to me how this is proposed to be done.
    
    Loading...
  - Craig permalink
    
    March 5, 2012 9:04 am
    
    Lewis,
    
    The error of quantum computerology is stated clearly in Scott Aaronson’s thesis, http://www.scottaaronson.com/thesis.pdf : He claims, “Either the Extended Church-Turing Thesis is false, or quantum mechanics must be modified, or the factoring problem is solvable in classical polynomial time.”
    
    There is a fourth alternative that he never considers: That quantum mechanics is correct, the Extended Church-Turing Thesis is true, and the factoring problem is not solvable in classical polynomial time… but that quantum complexity theory gives a bad model of reality. On paper, the cost of maintaining an n qubit machine may be polynomial, but in reality, the cost of maintaining an n qubit machine should be exponential, since the amount of information that an n qubit machine stores is exponential.
    
    In this world, there are no free lunches. Quantum computerology doesn’t take this into account. The fact that quantum computers haven’t been built, yet many have tried, confirms this.
    
    Also, since this post on this blog, I’ve looked into different interpretations of quantum mechanics. I’ve found them all to be correct in their own way, each illustrating different aspects of the theory. Most importantly, they each illustrate that QM is counterintuitive, but still not magic. However, quantum computing is magic.
    
    Loading...
  - aram permalink
    
    March 5, 2012 12:50 pm
    
    Craig wrote:
    
    On paper, the cost of maintaining an n qubit machine may be polynomial, but in reality, the cost of maintaining an n qubit machine should be exponential, since the amount of information that an n qubit machine stores is exponential.
    
    If that were true, Craig, that would be an important insight, worthy of a publication venue more glorious than comment #100 on a month-old blog post.
    
    But if you developed this idea further, you’d realize how deeply wrong it is. Or if not, then the referees would tell you.
    
    Loading...
  - Craig permalink
    
    March 5, 2012 1:44 pm
    
    What would their reasoning be?
    
    Loading...
  - John Sidles permalink
    
    March 5, 2012 2:25 pm
    
    Craig, the referees might suggest that your intuitions might be “dualized, then formalized.” That is (1) dualize the intuition by observing that FTQCs can efficiently error-correct quantum noise processes and can efficiently simulate quantum noise processes. Then (2) formalize the intuition with the help of articles like Riera, Gogolin,and Eisert’s recent “Thermalization in nature and on a quantum computer” ().
    
    Then analyze a Kalai-eque question (that now is well-posed): “Is it at all plausible that the set of thermalizing noise mechanisms that FTQCs are known to efficiently error-correct is partially or wholly disjoint from the set of thermalizing noise mechanisms that FTQCs are known to efficiently simulate?” Or in the opposite sense: “Can noise-free QCs efficiently simulate FTQCs that are exposed to thermalizing noise?”
    
    Before reading (arXiv:1102.2389v3), it would have been evident (to me) that the likely answers were “no” and “yes” … now it’s not so clear! 🙂
    
    The dualizing intuition is that the more nearly thermalizing noise approximates a Markovian process, the easier that noise is to error correct, yet the harder its dynamics are to simulate (although working through the details properly would be an immense amount of labor, needless to say).
    
    In any case, there does exist an accessible body of literature, and an interesting class of well-posed problems, that are reasonably suited to QM/QC/QIT students who are desirous of improving their intuitions and technical skills, and that broadly relate to “the costs of maintaining an $n$ -bit FTQC,”
    
    Loading...
  - Roger permalink
    
    March 5, 2012 5:06 pm
    
    None of these papers give any theoretical or experimental reasons for believing that the obstacles to quantum computing can be overcome. Craig’s hypothesis might be wrong, but I would like to see the paper that proves him wrong.
    
    Loading...
  - Lewis Mammel permalink
    
    March 6, 2012 10:37 pm
    
    Maybe a better mega-engineering analogy would be the space elevator, as popularized in Arthur C. Clark’s novel. In that case, every objection can be answered, it seems, yet there are good reasons to believe it will never be built, and never could be built. I also have to think of Archimedes’ boast, “Give me a place to stand and I will move the earth.” We might say, “Give me a Hadamard gate …”
    
    Loading...
  - Craig permalink
    
    March 6, 2012 11:14 pm
    
    aram said, “But if you developed this idea further, you’d realize how deeply wrong it is.”
    
    I would like to know where exactly the idea would go wrong if I tried to develop it further. By the way, I did not originate this idea.
    
    Loading...
John Sidles permalink

February 5, 2012 4:10 pm

The burden is on [QC skeptics] to answer [questions about] the laws of physics. Take your time …

Thank you for this terrific post, Scott! Because thinking about the laws of physics, and applying these laws in service of urgent practical and/or humanitarian challenges, surely is no “burden”, but rather is a sobering privilege that is intimately united with the great “adventure of our lives.”

Cristopher Moore’s excellent GLL post about photon entanglement offers us one good starting-point (among many). Let us imagine that Alice and Bob stand at opposite ends of a low-loss multi-fiber Aaronson-Arkhipov interferometer, and they seek to verify the predictions of standard QM at the highest feasible levels of photon entanglement.

Of course, as Alice installs photon sources, and Bob installs photon detectors, each of high-and-higher efficiency, the cavity-QED analysis of their apparatus becomes more-and-more intricate, to the point that the formerly sharp distinction between photon sources and detectors becomes wholly obscure.

With a view toward simplifying this navel-viewing maze of cavity-QED complexities, Alice and Bob therefore symmetrize their Aaronson-Arkhipov apparatus, by installing at the end of each fiber one trapped ion that is observed by one continuous Lindblad process, with each trapped ion serving simultaneously as a photon source and a photon sink. Thus each trapped ion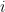 ${i}$ continuously observes current ${j_i(t)}$ , and the experimental record is simply the hierarchy of stationary-process correlation functions

$\displaystyle \big\{\,\langle\,j_i(0)\,\rangle, \langle \,j_i(0)\,j_k(\tau)\,\rangle, \langle\,j_i(0)\,j_k(\tau)\,j_n(\tau')\,\rangle,\,...\big\}$

Now, it so happens that Alice and Bob’s friend Carl is skilled in the computational art of simulating thermodynamic correlation functions (typically in a biomedical, solid-state, or quantum chemistry context). Moreover, Carl is filled with the blithe confidence that modern geometric (thermo)dynamics inspires, and so Carl offers to bet one pizza that he simulate Alice and Bob’s experimental data with a level of accuracy that is sufficient to pass any feasibly computable statistical validation test that Alice and Bob’s experimental data can pass.

“How can you make such an wager?” ask Alice and Bob. “My pizza is reasonably safe …” asserts Carl:

“Both Hamiltonian dynamics and Lindbladian processes naturally pullback onto product state-spaces of any desired rank. Moreover the basis of that product state-space can be chosen so that all the common conservation laws of physics are satisfied identically and independent of rank, and similarly resonant line-widths can be as narrow as required (independent of rank). Because all thermodynamic principles and dynamical conservation laws are satisfied identically, and because all mathematical operations are natural, no particular mathematical creativity or physical insight on my part is required to program the simulation.”

“In fact (aside from choices that depend mainly upon mathematical technique rather than inspiration) my main simulation design choice is the state-space rank that is required to model the correlation functions, and up to the present era no experiment ever conducted, in any laboratory, has required a simulation rank that is more-than-polynomial in the number of sources / detectors.”

“That is why I (Carl) am confident that you (Alice and Bob) are going to end-up buying me a pizza!” 🙂

As a quantum systems engineer, Carl appreciates the simplifying power of the mathematical naturality that is associated to modern geometric thermodynamics and dynamics, and yet Carl is utterly indifferent to the fundamental question of whether the state-space of Nature really is a Hilbert space: for Carl the main payoff of QM/QC/QIT research is the immensely powerful practical insight that Nature’s state-space is effectively a non-Hilbert product state-space — for Carl and his fellow engineers, the economic worth and the thrilling enterprises that are associated to this insight suffice to amply justify all the QM/QC/QIT research ever conducted.

Alice and Bob are left to wonder however “Gosh, maybe the state-space of Nature isn’t a Hilbert space.” And it is clear that Alice and Bob (and many physics colleagues) will have a busy time of it, investigating this question …\ and perhaps winning-back a pizza from their engineering colleague Carl! 🙂

Loading...

Reply
Gil Kalai permalink

February 5, 2012 7:50 pm

Dear all, there are several questions to me by Boaz and Chris which I will be happy to relate to ans also to some other comments. This will have to wait for one week. There are several issues we plan to discuss in the next posts and I prepared also a list of some further issues that were raised. (But again – next weekend.)

Let me make one “meta” comment which is simply to reapeat what I said here on the blog in June http://rjlipton.wordpress.com/2011/06/24/polls-and-predictions-and-pnp/#comment-12296 , and on several occasions earlier: Overall, I dont think that my work and other skeptical works should change people’s a priori beliefs on the feasibility of quantum computers. But I do think that the issues that I research and that we discuss here are interesting and important and I am very glad with the opportunity to discuss them.

Loading...

Reply
- Gil Kalai permalink
  
  February 6, 2012 4:51 am
  
  One more thing. I am very thankful to John Sidles for his beautiful comments.
  
  Loading...
  
  Reply
Robert Alicki permalink

February 7, 2012 9:47 am

Sorry, but my reply was somehow misplaced, and the separation between questions and answers dissapeared. I am very clumsy even with classical computers, so I try again.

Dear Aram, you have raised a number of very interesting questions, some of them concerning still quite controversial issues. To address them honestly one has to write a book, but as the discussion becomes more and more interesting and substantial , I try to sketch my point of view. Sorry, for repeating myself, but certain issues are notoriously confusing.

“I believe more in the possibility that interactions affecting a few terms at a time will still eventually drive the system to equilibrium. This is clearly possible with *some* sequence of two-qubit interactions; consider the quantum Metropolis algorithm of Temme et al.”

Yes, but this is a quantum algorithm performed on QC and cannot be effectively implemented classically while classical Metropolis works very well for classical systems. The difference between quantum and classical is that flips of individual spins commute and are good error operators for classical systems. Therefore, the result of sampling does not depend of the order of applied errors (flips). For quantum systems the error operators do not commute even for such “ almost classical” models like Kitaev ‘s (R.A. et.al. J.Phys.A.42, 2008). Therefore, for quantum models we need additional averaging over the permutations in the sequence of errors what could be done efficiently only on QC.
BTW, the fact that quantum error operators depend not only of the coupling to the bath but also on the Hamiltonian is appreciated only by a handful of experts. In hundreds of papers and dozens of books the authors simply add the convenient Lindblad generator to an arbitrary Hamiltonian. Some of them claim also that one can arbitrarily “design” Lindblad generators, e.g. to drive the system to the requested state.

“Another possibility is that systems are metastable and take exponentially long to reach their ground state.”

Why should it help FTQC?

“What I think is the more relevant possibility for quantum computing is that everything is far out of equilibrium, and work is continually performed to pump away errors and keep it that way.”

This is a very popular but wrong intuition. Imagine a system coupled to a bath at (almost) zero temperature which is driven to its (almost) ground state. The possible high initial entropy is reduced to (almost) zero but nevertheless the system ends in a unique final state i.e. does not contain any information about the initial input. What destroys information is not a high entropy alone, but also the always positive entropy production. Adding a non-equilibrium device like a refrigerator can reduce entropy but at the price of increased entropy production.

“But I have to take issue with the very last point you made, which is that we needed chaos to tell us that Newtonian dynamics could not produce super-strong analog computers. In fact, if you posit an infinitesimal but constant noise rate (like 10^-20), then analog computing pretty clearly fails, even without knowing anything about chaos. In other words, even if we had never heard of chaos, we’d be able to notice our inability to prove a threshold theorem for analog computing that could cope with i.i.d noise.”

What you propose is exactly one of the tests for classical and quantum chaos. If you add a bit of noise to a classical chaotic system you see that the entropy of the state grows linearly with time and the slope is practically independent on the noise magnitude. This slope is the Kolmogorov-Sinai entropy! The similar behavior is observed for many examples of quantum systems with chaotic classical counterparts but also for quantum systems with randomly chosen Hamiltonians (R.A. et.al PRL 77, 1996; J.Phys.A, 2007 and refs there). So, it is quite justified to say that this is a generic behavior.
Again , a popular but completely wrong intuition is that quantum systems are intrinsically more stable than classical because the Schroedinger eq. is linear in contrast to the nonlinear Newton eq.

“Are superconductors chaotic? BECs? Lasers? And a classical RAM chip is still described by quantum mechanics: if it is chaotic, how does it store a bit so well?”

Firstly, few remarks about quantum states, macroscopic quantum states and classical states, a notoriously confusing issue. Notice, that all systems are quantum, only the states can be classified as above, “classical systems” is a short-hand term for quantum systems in classical states.
Examples:
1) One or few phonon state of macroscopic diamond is a quantum state , but not macroscopic quantum. One can entangle such states for two diamonds (realized experimentally), but one cannot “entangle diamonds”.
2) A coherent state of 1000 phonons is a classical state.
3) A superposition of such a state with another one with 2000 phonons is a macroscopic quantum state (never realized).
4) Superconducting qubit states are quantum states, similarly to 1). They are superpositions of a ground state and a single-excited Cooper pair state (see arXiv:1012.0140, my previous preprints on this topic questioning a quantum character of Josephson qubits were wrong).
5) Superconducting states of macroscopic samples and BEC states are classical states. The corresponding “condensate wave functions” are classical objects (e.g., they satisfy nonlinear Ginzburg-Landau or Gross-Pitaevski equations). They cannot be entangled (similarly to waves on Lake Ontario with waves on Lake Sniardwy ), and there are useless for QI/QC. Amazingly, there is PACS 03.75.Gg Entanglement and decoherence in Bose-Einstein condensates.

Large superconductors, Lasers and BEC, which are classical, can display chaos in some range of parameters (some randomly found refs: Xu, et. al, Chaos in superconducting tunnel junctions, J.App.Phys.12, 1995; J.Ohtsubo, Semiconductor Lasers: Stability , Instability and Chaos, Springer 2010, K. Zhang, et.al, Hamiltonian chaos in a coupled BEC-optomechanical-cavity system, PRA 81, 2010). But those systems are also open systems operating in the classical regime. Environment not only selects classical states as the only relatively stable ones, but also adds friction to their dynamics. Friction can suppress chaos and “digitalizes” classical systems which can occupy discrete local minima of free energy separated from each other by macroscopic barriers. This is exactly the regime in which all classical computers operate. The price paid for stability is the work necessary to overcome friction which is dissipated into the system and makes classical gates irreversible. This does not harm classical computations, but I think, is deadly for quantum ones.

Loading...

Reply
- aram permalink
  
  February 7, 2012 12:50 pm
  
  Robert, your points are interesting. I hope to return to them soon, perhaps in a format less deeply buried on a comment thread.
  
  Loading...
  
  Reply
- aram harrow permalink
  
  February 7, 2012 2:05 pm
  
  Actually, I can probably express what I want to say concisely here.
  I agree with many of your points, but don’t think that their conclusions spell doom for FTQC. For examples, yes, quantum Kraus operators don’t commute, and we have only limited control over the Lindblad terms, but I don’t think these are fundamental difficulties.
  And yes, a FTQC will have to produce lots of entropy, but it’s ok as long as it dumps it somewhere else. Just like my desktop computer expels a lot of heat via its exhaust fan. Maybe this is bad for the environment, but the computer still works.
  
  I think your point about friction is crucial. I agree that it is necessary for QECC. But I think “friction” just means error-correction, and there, the repetition code is only one code among many. Error-correction in the Shor code is also a sort of friction, and this kind will protect both amplitude and phase information. While this has never been previously observed in nature, neither had large-scale classical computers until pretty recently, and in both cases the theory is simple enough that we can predict its behavior if we were to build it.
  
  Loading...
  
  Reply
  - Robert Alicki permalink
    
    February 8, 2012 5:15 am
    
    Dear Aram, I am happy that we were able to reduce a vast “battlefield” to a rather small “boxing ring”.
    
    Two comments:
    
    “For examples, yes, quantum Kraus operators don’t commute, and we have only limited control over the Lindblad terms, but I don’t think these are fundamental difficulties.”
    
    I think it is fundamental. Even very small inconsistencies in the “wishful -thinking” Lindblad or Kraus terms violate thermodynamics (it was noticed a long time ago that the Bloch equation for spin-1/2 with external control did it). These efects cumulate and produce a big “Maxwell demon” which can yield miracles.
    
    “And yes, a FTQC will have to produce lots of entropy, but it’s ok as long as it dumps it somewhere else.”
    
    So, you believe that one can always dump it somewhere else, I believe that the information bearing degrees of freedom always get their share.
    
    Loading...
  - Boaz Barak permalink
    
    February 8, 2012 9:53 am
    
    HI Aram, Robert,
    
    I don’t know much about physics, and in particular have no idea what Lindblad terms or Kraus operators are (though they sound like things I wouldn’t want to meet in a dark alley).
    
    I was wondering if it was possible to explain in a simplified matter to laymen like me what is your argument. If this is not possible or too much work then feel free to ignore the following.
    
    In particular, I’m wondering about the following question: suppose that I had a PC with a sealed case without a fan. Then presumably, it will only be able to run it for T computational cycles before shutting down. I imagine, perhaps wrongly, that this T is not an absolute constant, but rather something having to do with the size of the PC, and perhaps the amount of money I paid for it.
    
    So I guess my question is whether in quantum computing also, if I didn’t want a machine that runs forever, but only one that can handle T computational cycles, shouldn’t I be able to build one by spending f(T) dollars, for some function f()? This is of course a rephrasing of the question I asked Gil before, to which he promised an answer, but perhaps Robert/Aram have a different answer.
    
    Loading...
  - Robert Alicki permalink
    
    February 8, 2012 10:25 am
    
    Hi Boaz, I don’t know if Aram agrees with me, but my simple explanation is the following:
    
    Quantum computer uses not only probabilities that certain states are occupied (for example |0> or |1>), but also specifically quantum coherences described by certain complex numbers. Noise influences those probabilities what finally can lead to a situation when all states are equally probable – maximum entropy state, But this increase of entropy is associated to a heat exchange with an environment and can be reduced by cooling. Unfortunately, noise kills also the coherences. This is a process which does not change energy but only entropy, and therefore, I think , cannot be reduced by any type of cooling.
    
    So, you have to spend exponential amount of money, buy an exponential number of quantum computers, perhaps one of them give you a solution for your hard problem.
    
    Loading...
  - aram permalink
    
    February 8, 2012 11:44 am
    
    Boaz,
    if there are no fresh qubits and you have a constant rate of i.i.d. noise, then you get log depth (which, btw, suffices for Shor’s algorithm). That’s from this paper: http://arxiv.org/abs/quant-ph/9611028
    
    I agree with Robert about everything except the part where he says cooling is impossible; I would say cooling is impossible without bringing in fresh low-temperature states, or using up an initially given supply of these.
    
    Loading...
  - Craig permalink
    
    February 8, 2012 11:12 am
    
    Robert Alicki,
    
    Do you mean that in order to prevent n qubits from decohering into its maximum entropy state where everything is equally probable, one needs the order of 2^n energy, one unit of energy for each of the 2^n weight-probability-amplitudes?
    
    Loading...
  - Robert Alicki permalink
    
    February 8, 2012 11:28 am
    
    Of course not, I mean something completely different. You can easily supress entropy increase due to the change of populations (probabilities), because this entropy is related to energy (heat), but you cannot do anything effective to entropy increase due to pure decoherence (dephasing). Therefore, you do not have any exponential speedup associated with quantumnes (coherences). – for hard problems you need exponential resources.
    
    Loading...
  - John Preskill permalink
    
    February 8, 2012 12:13 pm
    
    It is useful to formulate the question mathematically. Then we can focus our attention on which assumptions in the mathematical arguments ought to be questioned.
    
    From a mathematical viewpoint, Robert Alicki’s statement that dephasing cannot be prevented by cooling is incorrect. The quantum accuracy threshold theorems show that if we have access to fresh qubits and the noise is sufficiently weak and sufficiently weakly correlated, then scalable quantum computing is possible. Cooling is required if we want to reuse qubits because we have only a limited supply available. Of course, cooling is also needed for fault-tolerant classical computing to work. Therefore, if we want to make a distinction between classical and quantum fault tolerance, we should take cooling for granted and consider where else the assumptions in the quantum threshold theorem could be wrong.
    
    Robert objects that the noise models assumed in threshold theorems are unphysical. But some of his objections apply only to Markovian noise. There are also threshold theorems that apply to non-Markovian noise models, and I have not understood why Robert objects to these noise models on fundamental grounds.
    
    In my earlier comment I gave an example: a Hamiltonian noise model such that a threshold theorem can be proven if the operator norms of the terms in the Hamiltonian obey a suitable criterion. Conceptually, this model has the nice feature that we don’t need to assume anything about the initial state of the bath beyond the assumption that is it possible to cool individual qubits (prepare a qubit in a state close to the standard “spin-up” state). This model may not be realistic, but why is it unacceptable as a matter of principle? It would be helpful if Robert or Gil could exhibit families of Hamiltonians which allow fault-tolerant classical computing but disallow fault-tolerant quantum computing. Such examples would help to clarify where the disagreement lies.
    
    Robert also mentions that during the course of a long computation the bath may be driven to a highly adversarial state “which can yield miracles.” We tried to address this worry in the paper I cited in my earlier comment, where we proved a threshold theorem for Gaussian noise. In that case we assumed a rather special type of noise model, in which the bath is a (linear) system of harmonic oscillators, and the intial state of the bath is Gaussian (for example a thermal state at some specified temperature). The noise can be completely characterized by the two-point correlation functions of the bath, and we showed that scalable quantum computing is possible if the correlation functions obey suitable conditions. During the computation the bath might be driven far from its initial state, but our argument shows that it does not become sufficiently “adversarial” to overcome fault-tolerant protocols.
    
    Here, too, the noise model is not fully realistic, but what is wrong with it as a matter of principle? Is it that we must include nonlinearities in the bath dynamics? Is it that the initial state of the bath will not be Gaussian? Is it that the correlation functions will not obey the conditions we assumed? Is it something else I am overlooking?
    
    Knowing precisely where the objection lies would make it easier for me to think about the problem. Actually, I tried to show that the threshold proof could be extended to the case where the bath is weakly nonlinear, but I ran into difficulties and got stuck. Would a result like that impress the skeptics? I have also tried to weaken the conditions on the correlation functions by making additional physically motivated assumptions, but that approach, too, has not yet succeeded. Is that an important direction to pursue further?
    
    Loading...
  - Robert Alicki permalink
    
    February 8, 2012 1:15 pm
    
    The problem with mathematical formulation is that we do not know exactly how far we can go with idealizations in our models. Just now I am working with my colleagues on models of cooling using “quantum refrigerators”. One can find very realistic models of systems which can be cooled to 0 K at finite time, what contradicts the III-law of thermodynamics. Nature does not allow for such a violation because those systems are always accompanied by others which cannot be cooled so fast.
    The first step which could help us to solve a FTQC mystery is the precise formulation of the procedures involving “fresh qubits” and the related minimal conditions necessary to prove threshold theorems. One can then try to construct the completely Hamiltonian models with realistic environments to test these conditions. “Fresh qubits” are also the part of FTQC which I cannot accept as granted, but there are more difficult to scrutinize than the assumptions about noise correlations. It seems they are a necessary ingredient also of the last papers of John.
    My second objection to the recent John’s models is the “small norm assumption” for the interaction Hamiltonian. Take a natural implementation – dipol-dipol coupling of spins. It can be indeed very small, but this coupling decays with the distance as 1/R^3. It means that the total norm for the interaction with a spin bath diverges logaritmically with the bath’s radius.
    Of course, one can say that the coupling could be screened, but for screening we need another degrees of freedom which produce their own noise, etc, etc.
    We do not really know which assumptions are really necessary to protect our models from anomalies violating e.g. the laws of thermodynamics. But we should try to find them!
    
    Loading...
  - John Sidles permalink
    
    February 8, 2012 12:53 pm
    
    John Preskill remarks: “The noise can be completely characterized by the two-point correlation functions of the bath.”
    
    This is true, and moreover, these same correlation functions completely characterize the renormalization of the qubit dynamics by the bath reservoir.
    
    As a practical example, to initialize a qubit as “spin-up” it is necessary to initialize (for example) image qubits residing in the walls of the vacuum chamber also as “spin-up”. In practice, as devices push the boundaries of sensitivity and computational efficiency, it commonly is observed that renormalization effects are order unity, rather than small corrections. Thus separating the computational state-space from the bath state-space is ubiquitously (in experimental practice) neither as mathematically natural nor as physically distinct as might be desired, and it is therefore entirely legitimate (AFAICT) to wonder whether fundamental obstructions may be associated to these renormalization mechanisms.
    
    Mathematically speaking, in the context of quantum computing, the familiar fluctuation-dissipation relations and Kubo-Green transport relations are thus realized as fluctuation-dissipation-transport-entanglement relations, and (again AFAICT) the large- $N$ and low- $T$ scaling behaviors of these (well-posed?) quantum entanglement relations are (potentially at least) among the topics of interest that Robert Alicki’s posts are highlighting.
    
    Needless to say, whether or not these renormalization relations are associated to fundamental QC obstructions, they definitely are associated to practical QC obstructions.
    
    Loading...
  - Robert Alicki permalink
    
    February 8, 2012 2:35 pm
    
    You are absolutely right, the renormalization problems become even worse when external time-dependent control is included. The same holds for the problem of separation of “physical dressed qubit” from the “baths”. But this is completely ignored by the majority QI community. I understand the local reasons at my University in Gdansk. The last obligatory course on quantum field theory including renormalization etc.was delivered by myself about 15 years ago. Later on this topic was regarded as to difficult for graduate students. But what about the leading world’s schools in USA, UK, etc.?
    
    Loading...
  - John Preskill permalink
    
    February 8, 2012 3:59 pm
    
    Robert: you remark that fresh qubits are “part of FTQC which I cannot accept … but … are more difficult to scrutinize than the assumptions about noise correlations.”
    
    It is true that all threshold theorems I know of assume that we can prepare fresh qubits with small, weakly correlated errors. Until this recent exchange, I had not appreciated that you are objecting to this assumption.
    
    Is your view is that no matter how hard we try to prevent it, the fresh qubits will have strongly correlated errors? If so, this seems to be a particular type of correlated noise, so why is it “more difficult to scrutinize”? And why doesn’t the same claim apply to classical bits? (Or does it?)
    
    Loading...
  - Robert Alicki permalink
    
    February 8, 2012 5:23 pm
    
    Assume, we have only one fresh qubit which is a spin-1/2 to avoid the problem of correlations. To preserve this spin in an almost pure state at finite temperature we need to keep it in a strong enough magnetic field. Then as I understand the “quantum cooling” , it is essentially a unitary swap between the fresh qubit and computer qubit. However, swap Hamiltonian does not commute neither with the strong magnetic field nor with the computer Hamiltonian. You can try to switch off them for the time of making swap. If you do it fast then such an impulse perturbs strongly the total system. If you do it slowly then magnetic field does not protect fresh qubit for a quite long time. To estimate the final result you need to solve a difficult problem of time evolution of an open system in time dependent external potential. I can find a suitable master equations in the regime of weak coupling to a bath only in two extreme cases: very slow time-dependence or fast enough periodic one. The first is useless, perhaps the second can model periodic rounds of EC. So, this is a new problem for the theory of open systems and it would be helpful if “QC-people” could explain clearly the whole procedure to allow proper modeling. For classical computers we must cool macroscopic object representing a bits – “cold bath”, from which refrigerator transports heat to a “hot bath” – external reservoir. This is not difficult to describe both in quantum and classical formalism.
    
    Loading...
  - aram harrow permalink
    
    February 8, 2012 6:27 pm
    
    Robert, I agree that the physics of this is complicated. But highly polarized spins *are* something we can create, in a variety of settings. Some of these settings don’t end up being useful for quantum computing, e.g. electronic states of Rubidium atoms. But their presence suggests that providing fresh nearly-pure input qubits is a (hard) engineering problem rather than a fundamental physics problem.
    
    Loading...
  - Robert Alicki permalink
    
    February 9, 2012 3:23 am
    
    Aram, you are right, experimentalist can do a lot. But I think it does not help much. Imagine a classical chaotic systems. The error grows in time t like A \exp{L t}. The experimentalists can improve the initial error A, but they cannot do anything about Lyapunov exponent L (related to K-S entropy). So they can only logarithmically improve the “life-time” of analog computation. The similar behavior is numerically confirmed in chaotic quantum systems, but of course not in terms of exponentially diverging trajectories, but in terms of entropy production (quantum K-S entropy, a possible keyword “Alicki-Fannes entropy” :)).
    
    Loading...
  - John Sidles permalink
    
    February 8, 2012 5:20 pm
    
    The way I parse one of the points that Robert Alicki has been making (and with which I agree) renormalization dynamics enforces a well-defined complementarity relation between mathematical rigor and physical rigor in FTQC. Specifically, fluctuation-dissipation-entanglement theorems ensure that the qubit-reservoir entanglement associated to ground-state renormalization is unphysically diverges in precisely the same Markovian limit for which the FTQC theorems exhibit their greatest power.
    
    The upshot (it seems to me) is that QC skeptics and QC nonskeptics alike are reasonably justified in deploring a general prevalence of hand-waving arguments, and a general lack of mathematical and physical rigor, specifically in regard to the tightly dovetailed dynamical flows that are associated to localization, renormalization, and decoherence.
    
    Loading...
Craig permalink

February 7, 2012 9:02 pm

This post has made me very uncomfortable, because it revealed to me how much I didn’t understand about the subject of quantum computing. I have lots of questions now, starting with how should I interpret quantum mechanics?

I found this very well written paper from 1996, which seems to give an answer to at least some of my questions: http://arxiv.org/pdf/quant-ph/9605002.pdf

I’ve never seen anything like this before and it’s not even listed in Wikipedia. I found it by listening to this Google talk: http://www.youtube.com/watch?v=dEaecUuEqfc

It’s good to watch the talk before you read the paper, but not required.

Loading...

Reply
Craig permalink

February 8, 2012 7:13 pm

I think this debate here is a lot like the debate between Creationism/Intelligent Design and Macro-evolutionism.

Macro-evolutionists believe it is correct to extrapolate backwards in time the fact that life is not static but dynamic in order to explain life’s origins, even though the odds of life originating from nonliving matter and developing into what it is today are so astronomically small.

Quantum-computerologists believe it is correct to extrapolate that because quantum mechanics has been found to be true for simple experiments, it must be true for complicated experiments (quantum computers), even though the amount of information that a large-scale quantum computer must hold is greater than the estimated number of atoms in the universe.

Loading...

Reply
- Rachel permalink
  
  March 7, 2012 2:21 am
  
  Look up Holevo’s Theorem (http://en.wikipedia.org/wiki/Holevo's_theorem). Holevo showed in 1973 that n qubits can represent only n classical bits of information. The “quantum computers hold an exponential amount of information” meme is wrong.
  
  Yes, an n-qubit quantum state can be in superposition over 2^n basis states. Quantum theory could break down in some magical way. Even classical mechanics could break down. Maybe if you flip a coin n times, there are only 1000 different possible result strings, regardless of n. Anything is possible. Maybe God will step in and change the laws of physics if we ever get close to building a quantum computer. He has managed to fool all of the world’s biologists into believing in evolution, so clearly He is very devious indeed.
  
  Loading...
  
  Reply
  - Craig permalink
    
    March 7, 2012 11:02 am
    
    Rachel,
    
    Holevo’s Theorem uses a different definition of information than I was talking about. My point of view is identical to the point of view given here:
    
    http://www.wisdom.weizmann.ac.il/~oded/on-qc.html
    
    There is an important difference between evolution theory and quantum computing that I didn’t mention: One cannot travel backwards in time to verify whether evolution explains how life originated. But one can travel forwards in time to verify whether quantum computing will become a reality.
    
    Loading...
  - aram permalink
    
    March 7, 2012 11:36 pm
    
    Craig, your arguments, like Goldreich’s, do a good job of identifying why many people don’t like quantum mechanics. Unfortunately for your side, quantum mechanics became the standard theory of physics after giving the only correct formulation of chemistry, thermodynamics, radiation, electromagnetism, and basically everything else outside of black holes. Many people have disliked quantum mechanics since it was invented, but no one has been able to change the basic model at all. Worse, any corrections from unifying with gravity are probably going to leave the low-energy theory pretty much unchanged, just as we still use Newton’s laws despite relativity. So we’re pretty much stuck with exponentially long vectors.
    
    As for what I wrote before, if you bothered to work through your theories, instead of asking people to do the work for you, you would find that any attempt to make Goldreich-style criticism sensible will fail to give anything coherent. Scott wrote a paper on this, but it’s better to try to work it out for yourself.
    
    Also, you *can* travel into the future to witness evolution.
    http://myxo.css.msu.edu/ecoli/
    
    http://xkcd.com/54/
    
    Loading...
  - Craig permalink
    
    March 10, 2012 9:09 pm
    
    Aram,
    
    I don’t have anything against quantum mechanics. I just don’t think quantum computing is feasible. I’ve already worked through my theories – maintaining exponential vectors requires an exponential cost. It’s that simple. I’m not relying on anybody to do the work for me. I read Scott Aaronson’s paper on Sure states and Shor states. I’m not moved by it.
    
    I think the recent quantum computing frenzy is another example of how people don’t want to be told that something is impossible. It’s similar to the P vs NP problem. This is the only famous math problem that I am aware of in which there are lots of people claiming P!=NP and lots of papers claiming the exact opposite, P=NP. Why are there so many papers out there claiming P=NP, when all of the evidence points to P!=NP? Because people don’t want to be told that something is impossible. P!=NP puts a limit on the ability of humans to solve problems, and most people don’t want to hear this.
    
    Loading...
  - aram permalink
    
    March 10, 2012 10:10 pm
    
    There are lots of papers proving P=NP and P!=NP because, with very few exceptions, they are all written by cranks. I would be wary of drawing any general conclusions from that.
    
    Restricting to the set of correct papers, there are more papers with algorithms than papers with lower bounds. Even NP-hardness proofs are basically algorithms. This is because an algorithm just requires proving that something you built works, but proving a lower bound requires ruling out all possible algorithms, which is something we are not very good at. Razborov-Rudich give some formal evidence along this line.
    
    If you accept quantum mechanics, then you’ll notice that the Hamiltonian for n 2-level systems has energy scale O(n), and requires 2^n dimensions to describe. End of story. Also, when an electron orbits a nucleus, what is the “cost”? Who is paying it?
    
    Loading...
  - Serge permalink
    
    March 10, 2012 10:00 pm
    
    Craig, I agree with all you’ve just said except for one fact: maybe P=NP but in any case we’ll never find the algorithm. Some yet unknown law of physics prevents us from finding the algorithm and from building a quantum computer as well. In fact we’ll never know whether P=NP. The set of algorithms is infinite but this kind of infinity is of no use in the real world. We can’t prove theorems like “there exists an algorithm such that …” without actually showing the algorithm. Complexity theory calls for new math and new physics: what common sense tells us is NOT that P!=NP. It tells us that efficient algorithms are harder to find than inefficient ones.
    
    Loading...
  - Craig permalink
    
    March 10, 2012 11:17 pm
    
    Aram said, “There are lots of papers proving P=NP and P!=NP because, with very few exceptions, they are all written by cranks. I would be wary of drawing any general conclusions from that.”
    
    The papers are written by all kinds of people. But why don’t people write papers that claim that Fermat’s Last Theorem is false? Because the implications of FLT are meaningless. But the implications of P=NP are not meaningless; hence, lots of people disagree.
    
    “If you accept quantum mechanics, then you’ll notice that the Hamiltonian for n 2-level systems has energy scale O(n), and requires 2^n dimensions to describe. End of story. Also, when an electron orbits a nucleus, what is the “cost”? Who is paying it?”
    
    I’m not claiming that exponential quantum states cannot exist in nature, only that most exponential quantum states, including the Shor state and the ones that would be necessary for a quantum computer to work, require an exponential amount of energy to generate and maintain. As evidence, I point to the fact that there are lots of papers about quantum algorithms, but still no quantum computers that can run the algorithms.
    
    Loading...
  - Lewis Mammel permalink
    
    March 11, 2012 8:57 pm
    
    Aram alludes to the quantum states of electrons in atomic orbitals. I have trouble reconciling the physics and the calculations of atomic states with the seemingly glib presumptions about the various quantum gates among qubits. If you look at the Wikipedia article on “configuration interaction” you will see mentioned that the calculations of such are very difficult and expensive computationally. Here are simple quantum systems which tax our ability to model them mathematically, yet the premise of quantum computing is that a simple quantum system can be constructed which do certain difficult and expensive calculations for us in an automatic way. I have trouble reconciling this dissonance.
    
    Another vexing question to me is the question of indistinguishability. This is an extremely important part of atomic physics and quantum physics generally, yet I never see mentioned whether qubit states are to be bosons or fermions, or how the particle exchanges are to be treated. I thought photon indistinguishibility was central to their “entanglement”, since it is just the symmetric wave function AB + BA, which expresses this.
    
    Loading...
  - aram permalink
    
    March 11, 2012 9:12 pm
    
    Lewis captures what is beautiful about quantum computing when he says:
    
    I have trouble reconciling the physics and the calculations of atomic states with the seemingly glib presumptions about the various quantum gates among qubits. If you look at the Wikipedia article on “configuration interaction” you will see mentioned that the calculations of such are very difficult and expensive computationally. Here are simple quantum systems which tax our ability to model them mathematically, yet the premise of quantum computing is that a simple quantum system can be constructed which do certain difficult and expensive calculations for us in an automatic way. I have trouble reconciling this dissonance.
    
    Indeed, it is hard to simulate quantum systems, because in the worst case things are exponential in the number of degrees of freedom, and our methods for taming this exponential dimension in special cases of interest are a complicated and incomplete patchwork.
    
    And yet Nature does this somehow every second! Fire a proton at a nucleus and Nature will have no problem calculating its scattering cross section. Strongly interacting systems are so difficult to solve that it’s at the limit of our abilities to even estimate the mass of the proton, and yet when you try to weigh something, Nature never gives you an hourglass symbol or spinning beach ball.
    
    Feynman’s genius idea in proposing quantum computers is that we can manipulate quantum systems into doing these simulations for us, instead of using our crude classical computing tools. As a result, we no longer have to pay the exponential price that our classical simulations paid.
    
    Another vexing question to me is the question of indistinguishability.
    
    Different systems have different answers to this. But to see the general idea, consider encoding n qubits into n Hydrogen spins. If these protons are well localized at positions r_1, …, r_n, then the wavefunction looks something like
    1/sqrt(n!) sum_{\pi in S_n} |r_{pi(1)}> \otimes |s_{pi(1)}> \otimes … \otimes |r_{pi(n)> \otimes |s_{\pi(n)}>,
    where S_n is the group of permutations of n objects, \otimes is the tensor product and s_1, .., s_n are the spin degrees of freedom.
    If we can address the spins according to their position, then we can treat this as equivalent to the simpler system
    |s_1> \otimes … \otimes |s_n>
    
    People in the QC community usually skip this first step, because in most implementations it’s not that interesting.
    
    Loading...
  - aram permalink
    
    March 11, 2012 9:30 pm
    
    Also, Lewis writes:
    
    I thought photon indistinguishibility was central to their “entanglement”, since it is just the symmetric wave function AB + BA, which expresses this.
    
    This is a slippery issue.
    Let me say briefly that it’s certainly not “central” and it is somewhat debatable whether this state is entangled at all. I am not an expert, but here are some papers that discuss this issue if you want to read more:
    
    http://arxiv.org/abs/quant-ph/0403119
    http://arxiv.org/abs/quant-ph/0507189
    http://arxiv.org/abs/quant-ph/0601079
    
    In any case, this is generally NOT the sort of entanglement that people propose to use for quantum computing and communication.
    
    Loading...
  - KWRegan permalink
    
    March 11, 2012 11:15 pm
    
    Regarding this in Aram’s comment above:
    
    And yet Nature does this somehow every second! Fire a proton at a nucleus and Nature will have no problem calculating its scattering cross section. Strongly interacting systems are so difficult to solve that it’s at the limit of our abilities to even estimate the mass of the proton, and yet when you try to weigh something, Nature never gives you an hourglass symbol or spinning beach ball.
    
    Feynman’s genius idea in proposing quantum computers is that we can manipulate quantum systems into doing these simulations for us, instead of using our crude classical computing tools. As a result, we no longer have to pay the exponential price that our classical simulations paid.
    
    Dick and I approach this issue as one about the primacy of notation. We regard notation as inherently classical, under part of the poly-time Church-Turing thesis that we regard as simply true. Put one way, we are disturbed by the idea of an atomic notation for a non-P-time process such as “(QFT x)” or “(Shor x)”, and see some support in papers like this and this noted to us by Aram, plus this and very recently this by Martin van der Nest (along with other work by him which we are having to examine more closely). We certainly believe that Nature does not “compute with exponentially long vectors” vectors, and we recognize that Dirac notation provides a great lexical savings by representing tensor products as concatenations, but we feel something besides it is needed to tell the story in the cleanest way.
    
    Loading...
- John Sidles permalink
  
  March 7, 2012 9:48 am
  
  Rachel, perhaps a reasonable alternative to conceiving “quantum mechanics breaking down in a magical way” is conceiving “quantum mechanics emerging in a natural way” … and this second point-of-view induces greater sympathy to Craig’s questions.
  
  It definitely is true that (in Feynman’s phrase) “The fundamental laws of physics, when discovered, can appear in so many different forms that are not apparently identical at first, but, with a little mathematical fiddling you can show the relationship.”
  
  That is why a Great Truth of quantum mechanical pedagogy is this: “Students should learn quantum mechanics as early as possible, preferably at the undergraduate level, and thus necessarily via the simplest physical examples analyzed by most elementary mathematical techniques. Because learning time is precious!”
  
  This being a Great Truth, we know its opposite is a Great Truth too: “Students should acquire broad foundations in mathematics before learning any quantum mechanics, and thus be equipped to conceive any and all quantum mechanical postulates — with reasonable fluency — equivalently within algebraic, geometric, analytic, and computational frameworks. Because mathematical naturality is precious!”
  
  Either way, it is essential to learn to fluently translate among many kinds of physics and many kinds of mathematics. For warm-hearted inspiration in this regard, tempered by realistic appreciation for the immense difficulties of mathematical learning, the sidebar links of Terry Tao’s What’s New weblog are a good resource.
  
  Loading...
  
  Reply
Gil Kalai permalink

February 9, 2012 12:53 am

Dear all, one additional rather important point about Chris’s first remark.

I mentioned my opinion that universal quantum computers that can create (up to negligable errors and using encoding) an arbitrary quantum evolution and arbitrary states described by them, represent a new physical reality. Chris wrote ” I don’t think this is correct. Quantum computers will simulate quantum systems in exactly the same way that classical computers simulate classical ones.” Chris is correct, this is excactly like classical computers simulate classical evolutions, but I am also correct that this is an entirely new physical reality.

Transferrng our intuition and experience from classical computers to quantum ones, cannot be taken for granted. In fact, to a large extent, this is the essence of the discussion between Aram and me.

Loading...

Reply
Robert Alicki permalink

February 9, 2012 4:09 am

Short comment on the John’s model:

“Conceptually, this model has the nice feature that we don’t need to assume anything about the initial state of the bath ”

This is exactly what worries me. Classical mechanisms of stability depend on the baths temperature i.e, on “initial state of the bath”. For temperatures above a certain critical model-dependent one the free-energy barriers dissappear and the system cannot encode any stable information. So in some sense John’s model is “to good to be true”.

Loading...

Reply
Blaze Townsend permalink

February 10, 2012 4:26 am

All I am going to say is that the nose on many animals are quantum computing devices. They receive information that reliably gives us an idea of what we are smelling and tasting. Quantum computers use a similar method of defining information (qubit). If noise is an issue, then rerunning the calculation to determine error values can be a solution. This can take the median of data charted in software to determine said noise values. Though without doing math on it, I suspect that error values in a slight vacuum or lower physical temperatures wouldn’t be hard to over come. Most particles run in predictable formations after all. And the lower the amount of particles or slower the particle movements, the easier to predict they become.

Loading...

Reply
- Craig permalink
  
  February 10, 2012 11:18 am
  
  Blaze,
  
  You could be right. One time, I visited someone’s house and pet their dog. Then I came home to my own house and my dog knew right away that I had pet another dog, as she was sniffing my pants for a long time.
  
  How did she know?
  
  Probably the smell of the other dog became entangled with my pants, and my dog was able to disentangle it by measuring it with her quantum computer nose.
  
  Loading...
  
  Reply
Serge permalink

February 20, 2012 6:28 pm

It is the same physical phenomenon which prevents mathematicians from devising quick algorithms to well-known supposedly hard problems, and which also prevents computer engineers from building quantum machines for solving the same hard problems more quickly. Both attempts are doomed to failure and this is why I believe P=NP. NP-complete problems can’t be solved quickly for reasons that belong to physics, not to mathematics.

Loading...

Reply
Yogi permalink

February 23, 2012 5:28 am

I am a grad student in Electrical and Computer engineering and work on quantum circuit synthesis. Most of the time, the cost of synthesizing quantum oracles (for example, the decision oracle in Grover’s search) is ignored by considering it as a black box – which is not the case for an an experimentalist.

Even if QC is possible in theory,using the gate model of QC, the sheer quantum circuit complexity of the decision oracle (without considering FTQC) becomes quite unmanageable as the size of the problem increases. Now, theorists don’t care about this. They state things in terms of query complexity – like Grover’s search requires O(sqrt(N)) calls to the quantum oracle as opposed to O(N) calls to a classical oracle.

The question is: is the complexity of the classical and quantum oracles comparable? In theory, yes; from practical quantum circuit design, NO. The quadratic speedup actually vanishes and a QC doing a Grover’s search would be slower than a classical computer unless it has really high clock frequencies.

This is intuition gained from experience and hard to construct as a theory.

( Personally, i am tired of this field. No one in the job market cares about my thesis anyways! Wasted 6 yrs in grad school. moved to parallel programming. )

Loading...

Reply
John Sidles permalink

February 23, 2012 5:19 pm

Yogi posts: I am a grad student … and work on quantum circuit synthesis … Personally, I am tired of this field. No one in the job market cares about my thesis anyways! Wasted 6 yrs in grad school.

Yogi, I hope you don’t mind an appreciation of your post that regards it as expressing a “Great Truth” of QM/QC/QIT (that is, a truth whose logical opposite also expresses a Great Truth). The duality of the Great Truths of science — and their close kin, the “Burning Arrows” of novel math postulates — has been a perennial theme here on GLL.

Because your particular great truth, Yogi, is particularly important to us all, and yet it is a particularly sensitive great truth, perhaps it is worthwhile to make a case for both sides of it. For raw material, we adopt version 1.0 of the “Quantum Information Science and Technology (QIST) Roadmap” (LANL document LA-UR-02-6900, 2002), which is a document that is familiar to many GLL readers.

Inspired by Yogi’s post, and benefiting too from a decade of experience, what Great Truths can we distill as lessons-learned from that 2002 QIST Roadmap?

Great Truth #1:Read as a “Roadmap,” QIST 2002 failed dismally

Prima facie evidence for Great Truth #1 comes in the form of this timeline (quoted verbatim from the QIST 2002 Roadmap): By the year 2007: encode a single qubit into the state of a logical qubit formed from several physical qubits; perform repetitive error correction of the logical qubit; and transfer the state of the logical qubit into the state of another set of physical qubits with high fidelity
By the year 2012: implement a concatenated quantum error-correcting code. It is sobering-yet-evident — for example, from the discussions here on GLL — that in 2012 there exists no clear roadmap for achieving the above QIST Roadmap goals by qubit technologies that are known to be scalable.

Still more sobering — especially for career-launching students like Yogi — is that there has been (to my knowledge) no structured review of why the QIST Roadmap’s milestones were so badly missed. Moreover, none of QIST’s Technology Experts Panel (TEP) ever comment in this regard on public forums like GLL, The Quantum Pontiff, Shtetl Optimized, the GASARCH/Fortnow weblog (etc.). This silence is demoralizing for everyone. 🙁

Moreover, perhaps other researchers have had experiences like the following: a high-ranking ARDA manager challenged me, in an elevator, by asking “Briefly, what have we got for our $500M investment in QM/QC/QIT?” It was not easy to answer this (literally) “elevator question” … and yet it is an entirely reasonable question.

So perhaps GLL is a venue where such an “elevator answer” might be conceived, valid for both graduate students and program managers (the former being considerably the harder audience!), within the stimulating context that the Kalai/Harrow debate provides?

Great Truth #2:Read as a “Guidance,” QIST 2002 succeeded brilliantly

This post is getting to be a bit long, so in regard to “Great Truth #2” I will make just one point, with the hope that it will stimulate further comments from GLL readers.

Ten years in retrospect, QIST 2000’s focus on a “Quantum Computing Roadmap” was doubly problematic: (1) quantum computing was too narrow a focus, and (2) roadmaps offer insufficient scope for the learning-and-adapting that quantum technology development requires.

To be sure, back in 2002 QIST’s roadmap focus was not obviously wrong. Indeed the semiconductor industry’s International Roadmapping Committee (IRC) had been brilliantly successful. None-the-less, nowadays we appreciate that quantum computing, both then and now, is not suited to an IRC-style roadmapping/timelining effort.

Let us suppose, therefore, that now is a good time to articulate a Great Truth #2 that affords to Yogi’s generation of students sufficient technological scope and narrative clarity to generate family-supporting jobs and dignified career opportunities, in the required super-abundance that a planet of seven billion people required. And in service of this ambitious goal, we can embrace the archetypal GLL “Burning Arrow” strategy of changing even the language in which the new Great Truth is stated.

In light of lessons-learned from QIST 2002, it is reasonable to avoid language associated to a “quantum computing roadmap”, and the central spotlight may even have to shift away from “quantum computing”per se.

Our own UW/QSE group is testing an environment that pulls back the key QIST ideas to a research venue that is associated with a broadened terminology: Intent ${\Leftarrow}$ Deliverable Guidance ${\Leftarrow}$ Roadmap Learn-and-Adapt ${\Leftarrow}$ TimelineThis new broader terminology is sufficiently adaptive that the wonderful merits of the fundamental quantum research catalyzed by QIST 2000 are appreciated within it, and even the now-traditional goal of achieving practical quantum computing can be pursued within it.

Please let me say that other adaptations are entirely reasonable, for the common-sense reason that quantum research has entered into a period of creative rethinking, and during such eras it is neither feasible, nor necessary, nor desirable that everyone think alike.

Fortunately, we can all be completely confident that good answers to concerns like Yogi’s can be evolved, and will be evolved, and even now are being evolved. And this is an appropriate unifying focus here on GLL! 🙂

Loading...

Reply
- aram harrow permalink
  
  February 23, 2012 8:35 pm
  
  I think you make some great points about QIST being at once too optimistic and also too narrowly focused on quantum computing, rather than quantum information processing more broadly. I don’t think the excessive optimism is a problem with the idea of quantum computing so much as the way researchers interact with roadmaps and with funding agencies.
  
  Loading...
  
  Reply
Serge permalink

March 5, 2012 4:35 pm

> “If blogs like GLL were around centuries ago there might have been a more penetrating discussion than even the Royal Society could foster.”

One thing I can say in favor of quantum computing is, in 1670 the idea of a blog like GLL would have sounded even more magical than quantum computers do today. 🙂

Loading...

Reply
- Lewis Mammel permalink
  
  March 8, 2012 6:48 pm
  
  I just read Feynman’s 1985 Optics News article on Quantum Mechanical Computers, and the concept he discusses, which he passes off as “entertaining nonsense”, is very quotidian compared to the post-Shor’s theorem stuff on the table today. There the “bits” are simply “written on atoms”, and controlled by reversible quantum operations in strict analogy to existing binary computer designs. He considers the entire machine to evolve according to some hypothetical Hamiltonian . What I’m saying is that you might as well say 1985 as 1670 when it comes to the magicality of the current conceptions.
  
  Loading...
  
  Reply
  - Serge permalink
    
    March 8, 2012 7:29 pm
    
    If I had the money, I’d be ready to offer $1,000,000 to the first builders of a true quantum computer!
    
    Loading...
Teresa Mendes permalink

April 29, 2012 12:15 pm

There are some new posts on Scott Aaronson’s blog. Do you care to participate?
http://www.scottaaronson.com/blog/?p=902#comments

Loading...

Reply
- aramharrow permalink
  
  April 29, 2012 12:48 pm
  
  My reply is here.
  
  Loading...
  
  Reply
- Teresa Mendes permalink
  
  May 3, 2012 7:39 am
  
  Scott Aaronson: Let me try to summarize where is stand and ask you some thing very important.
  
  In February 2012, Scott Aaronson, MIT specialist on Quantum Computing, waged publicly an $100.000 prize for someone that proved, to you, that a scalable quantum computer would be impossible to be built.
  J.Especial accepted his challenge presented a recently published article on Bell Inequalities.
  Scott, Especial, me and other scientists collaborated in this two day discussion, asking questions and posting opinions.
  
  Finally I asked Scott if he agreed that without entanglement it would not be possible to build a quantum computer. And he said yes!
  
  http://www.scottaaronson.com/blog/?p=902#comment-43238
  
  And now my important question for Scott is:
  Considering that you, or someone you trust, need time to revise in detail Especial’s article, and then you come out of that process agreeing with the conclusions of the article, which are – that there is no experimental evidence to this date, for you or anyone else, to claim that entanglement is a real phenomenon – is this sufficient for you?
  Do you want to suggest names of someone you trust – EPR specialists , mathematicians, physicists – and continue this discussion in a more solid scientific ground?
  
  Let’s do it together. It is not about the money. It is about the Prize.
  I do think there is a win-win situation for you, me, Especial and the whole world.
  You said : (I took all the money parts out of your phrase because that is not the point now)
  “The reason I made my […] bet was to draw attention to the case that quantum computing skeptics have yet to offer. If quantum computing really does turn out to be impossible for some fundamental reason, then [….] , I’ll be absolutely thrilled. Indeed, I’ll want to participate myself in one of the greatest revolutions in physics of all time, a revolution that finally overturns almost a century of understanding of quantum mechanics.”
  And that was the reason I approached you.
  
  With your help we can get the attention of the Physics Community to this unfortunate mistake that has huge implications in the our future and our children’s future.
  Waiting for your reply
  Teresa Mendes (on behalf of Teresa Mendes)
  
  Loading...
  
  Reply
  - aramharrow permalink
    
    May 4, 2012 1:41 pm
    
    There is evidence of entanglement. It’s arguably indirect evidence. But when you add it all up it’s overwhelming.
    
    Loading...
  - schlafly permalink
    
    May 4, 2012 2:21 pm
    
    Yes, there is overwhelming evidence of entanglement, but not the sort of entanglement that would be needed for a qubit computation.
    
    Loading...
  - The Author permalink
    
    December 17, 2012 5:31 pm
    
    Well here’s what old Musatov says, “It’s better to be indirect than outdirect, or worse without directive and bijective subjunctive looking for the lost div of the house of Israel”
    
    Loading...
Teresa Mendes permalink

May 6, 2012 4:23 pm

Aram: A large number of inconclusive experimental results does not become
conclusive evidence no matter how large that number may be. It’s a matter of
quality not of quantity.

Bell’s theorem directly applies only to ideal EPRB experiments. Since real
experiments to this date have never been ideal, it is incorrect to directly
apply Bell inequalities valid only for ideal experiments to these non-ideal
experiments.

Bell’s theorem needs to be generalized to non-ideal conditions, using some
additional hypothesis (e.g. “fair-sampling detection” when the non-ideality
in question is inefficient detection) and only then can the generalized Bell
inequalities be used to test the experimental result against the conjunction
of local-realism with the additional hypothesis.

The problem is that the generalizations made by Clauser and Horne in 1974
and by Garuccio and Rapisarda in 1981 are wrong and in consequence the
conclusions that have been drawn from the experimental evidence using them,
namely that the conjunction of local-realism with fair-sampling detection
has been rejected, is also wrong.

The correct generalized Bell inequalities have just been published by
J. Especial (http://aflb.ensmp.fr/AFLB-371/aflb371m746.pdf) and when these are
used to interpret the experimental results it is found that all published
experimental evidence is indeed compatible with the conjunction of
local-realism and fair-sampling detection.

This is why the situation has very recently changed.

Loading...

Reply
Gil Kalai permalink

May 30, 2012 1:20 pm

I systematically referred to Cris as Chris. I apologize for the mistake. –Gil

Loading...

Reply

	joe12361 on Just Jim
	T Nguyen on COMPUTATION, LOGIC, AND INFORM…
	Umayr on 1968 vs 2024
	javaid aslam on 1968 vs 2024
	Ian Z aka nobrowser on 1968 vs 2024
	Enough is enough on 1968 vs 2024
	rjlipton on An Open Problem
	Jordan on An Open Problem
	Jon Awbrey on An Open Problem
	Blog Runner on An Open Problem
	William Gasarch on An Open Problem
	DL on An Open Problem
	Jon Awbrey on An Open Problem
	An Open Problem \| Gö… on Cargo Cult Redo
	oblomovitis on Women in Math Research

a personal view of the theory of computation

Perpetual Motion of The 21st Century?

Guest Post: Gil Kalai

Conjectures on noisy QC’s and error-correction

Conjectured Limit on Entanglement

Interpreting and Testing the Conjectures

Why I Believe My Conjectures

Aram Harrow: A Short Response

Response Road Map

Open Problems

Like this:

Related

Trackbacks

Leave a ReplyCancel reply

Subscribe to Gödel’s Lost Letter

Our Book

Recent Posts

Top Posts

Recent Comments

Blogroll

Archives

Sitemeter

a personal view of the theory of computation

Perpetual Motion of The 21st Century?

Guest Post: Gil Kalai

Conjectures on noisy QC’s and error-correction

Conjectured Limit on Entanglement

Interpreting and Testing the Conjectures

Why I Believe My Conjectures

Aram Harrow: A Short Response

Response Road Map

Open Problems

Share this:

Like this:

Related

Trackbacks

Leave a ReplyCancel reply

Subscribe to Gödel’s Lost Letter

Our Book

Recent Posts

Top Posts

Recent Comments

Blogroll

Archives

Sitemeter

Discover more from Gödel's Lost Letter and P=NP