The Quantum Super-PAC
What unlimited contributions might buy you in power
John Preskill is no stranger to high finance in physics. In 1997 he made a famous bet against Stephen Hawking and Kip Thorne relating to the black hole information paradox. Hawking conceded the bet in 2004, but Thorne has yet to agree. The prize was an encyclopedia of the winner’s choice, which for Preskill was Total Baseball: The Ultimate Baseball Encyclopedia.
Today we present the third of three installments of Aram Harrow’s initial response to Gil Kalai’s argument against the feasibility of building large-scale quantum computers. We also survey reactions to a short paper that Preskill wrote in response to the arguments earlier this month, and note a writeup by Harrow and Steve Flammia about Kalai’s “Conjecture C” and related matters.
Preskill was joined by several other physicists including Leonard Susskind, who wrote a popular book The Black Hole War on the episode and its science. Hawking’s own theory that black holes eventually evaporate is now generally accepted, but sharpened the perception that information falling into the hole is lost. Preskill’s side argued that unitarity in quantum mechanics entails that all information is preserved even in this case. In a lecture posted on his website in 2010, Hawking gave “what I think is the resolution”:
Information is not lost, but it is not returned in a useful way. It is like burning an encyclopedia. Information is not lost, but it is very hard to read… I gave John a baseball encyclopedia, [but] maybe I should have just given him the ashes.
That might have been appropriate in cricket, where The Ashes series are contested between England and Australia for a trophy that really holds ashes. We may ask, what is the computational complexity of decoding information from a black hole? The complexity doesn’t stop the hero of a children’s book written by Hawking with his daughter Lucy from being resurrected out of a black hole.
Susskind subtitled his book as a battle “to make the world safe for quantum mechanics.” Some feel that quantum computers are in exactly the same battle, as even reflected in comments on the original post and responses one and two. In this third response, Aram Harrow tests the principles by allowing unlimited resources to build QC’s in outer space with all due shielding, in ways at least one Republican presidential candidate would entertain. Since probable approximate correctness (PAC) is often good enough for QC’s, we can call them Super-PACs.
Aram Harrow Part 3: Throwing (Imaginary) Money at the Problem
For this final part, suppose we approach quantum computing with an attitude of extreme pessimism. Suppose that anything non-classical that can be correlated, probably is, and in the way that we’d least like. Might Gil Kalai’s conjectures hold in this case, and prevent the construction of a large-scale quantum computer? I will argue that even in this case, by using unlimited resources we could build a quantum computer that would address even the most dire pessimism.
One approach would be to put the quantum computer in a place where there is very little noise other than what we introduce ourselves, like interstellar space. Then the individual components could be placed far apart, so that we are very unlikely to introduce multi-qubit errors by our inadvertent actions on shadow qubits.
For example, we might construct a linear optics quantum computer with each gate a kilometer apart. Correlations between noise processes on different qubits should be essentially zero, except when qubits are interacting. The threshold theorem does allow for correlated errors among interacting qubits—this is a standard assumption.
This approach would not eliminate the usual sources of noise. Each gate would be subject to control errors, and thus two-qubit gates would introduce correlated errors on the pair of qubits they act on. Presumably there would also be storage errors, as photons get absorbed by interstellar dust, as well as timing and other types of errors.
So what does this achieve? Let us recall how the crux of the second response involved “shadow qubits” as the main agents possibly interacting with the “computation qubits” and amplifying errors as the computation progresses.
Keeping Shadow Qubits in the Dark
One thing that I can be confident about suppressing here is the possibility of shadow qubits creating maliciously correlated decoherence. Shadow qubits can live on the individual circuit elements, such as beam splitters and photon sources. But they can’t really follow the photons from gate to gate, because even an infinitesimal change in direction is likely to make them miss the target.
But what about beam splitters that maliciously remember every instruction given to them, and choose their errors to foil the computation? Let’s allow them to do whatever they want to our qubits, as long as the per-gate error rate is below the current threshold allowance of . This includes a beam splitter biding its time for
steps and striking only when it judges that the time is right. But when is the time right?
To defeat a QECC, the beam-splitter needs to save its powder until its confederates all introduce errors at the same time. But it can’t really communicate with them. If our qubits lived on some superconductor then we’d have photons and phonons flying all over that different circuit elements could conceivably use to communicate. In space, though, there’s no real mechanism that circuit elements can use to coordinate.
Of course, there is something flying across the void between far-flung optical elements: the photons we use for the computation. But they can’t carry too much extra information, because adding information to them would cause errors, and would violate the constraint that the single-qubit error rate is . We are protected, again, by the linearity of quantum mechanics.
A similar situation is found in blind quantum computation (see Joe Fitzsimons’ comments for more on this), or this scheme for using randomness to code against adversarial channel noise. In each case, we can hide the computation, or the message, from the environment. For blind computation, this enables something like homomorphic encryption, while for the channel coding scenario, this means that even though there exists an adversarially chosen low-weight error that could corrupt the data, an adversary without knowledge of the random seed is unlikely to guess it.
Let Us Ignore Extreme Models
Of course, even these approaches can’t rule out extreme pessimism. If our universe began at a single point, then there are no truly causally independent points. This has been proposed as a loophole to Bell’s theorem: if the two parties are entangled from birth, then even if they believe they are choosing their measurements independently at random, they might nevertheless be unconsciously guided by a cosmic conspiracy. One variant of this idea is called super-determinism. Another possibility is that we are living in a simulated universe, whose rules naturally are subject to change at any time; e.g. our simulators could themselves trip over the power cord. Such levels of conspiracy could also derail arguments for classical computing and all of science, and I don’t think Gil intends to go there.
Intermediate Models
Let’s turn to a non-extreme area where Gil and I are closer to agreeing.
One fascinating open problem is to determine the power of quantum computers that do not perform fault-tolerant gates. On the one hand, this is an important practical problem, since experimentalists are currently building 5-10-qubit quantum computers, and perhaps soon we can imagine quantum computers with 100 or so qubits. These computers are too small or hard-to-control for FTQC using the constructions proposed so far, but still we’d like to do something interesting with them.
One fascinating, and under-theorized, example of this comes from Markus Greiner’s lab, which has put tens of thousands of atoms into optical lattices, where they can be used to simulate quantum systems such as antiferromagnetic spin chains. These sizes are far beyond what we know how to simulate classically, but on the other hand, the qubits are too noisy, and insufficiently addressable, to allow for general-purpose quantum computing. How can we meaningfully define a universal quantum computer without giving it the ability to correct errors?
Pretty much all attempts to do so have resulted in models equivalent to log-depth quantum computing, or in classically-simulatable models. But these results don’t give a full answer to the theoretical question of how to define non-fault-tolerant QC, nor to the practical question of what we can do with 100 qubits that experience a noise rate of 5% per gate.
This relates to some of the open questions that Gil mentions. He refers to noisy cluster states and noisy anyons. But we can also consider noisy adiabatic evolution, noisy linear optics, noisy IQP, or the NMR-inspired DQC1 model. Each is a fascinating candidate for classes intermediate between BPP and BQP.
Finally, we are starting to discover a few settings in which quantum error-correction is known not to apply. For example, suppose we do a Grover search using an oracle that fails (by doing nothing) with probability . Against this type of error, quantum error-correcting codes are worthless, and the Grover speedup vanishes. More generally, techniques from quantum information often yield quadratic improvements in estimating physical parameters, but in many cases, these disappear in the presence of a constant rate of noise.
Quantum information processing is about more than just building better computers, and as we move forward, it’s going to be important to understand just how much of a problem noise is. Especially while much of our field is in a theoretical phase, we need more people like Gil to play “Eve’s advocate” and push forward increasingly sophisticated theories of how noise can foil us.
Gil’s Third Rejoinder: Imaginary computers and Woodstock
A quiet intergalactic setting will not remain quiet once we put our device there.
More specifically, Aram wrote: “One approach would be to put the quantum computer in a place where there is very little noise other than what we introduce ourselves.” Right! This is an important distinction: the noise I am talking about all along is the noise we (or the quantum device) introduce and not some harmless background noise.
Aram’s suggestion to choose a quiet intergalactic place reminds me of Woodstock. I have a “Woodstock number” of 2, since Jeff Kahn with whom I wrote some of my best papers was actually in Woodstock. Woodstock was a place with very little noise, but when you run a concert for a million people in this noiseless place, it will be noisy—in principle!—no matter how much money you throw at it.
Generally speaking, I do not think that imaginary unrealistic quantum computers can be used to “fight” my conjectures. After all, we agree that QM allows to express the idea of a universal quantum computer. If you give me an unrealistic QC that violates, say, the strong principle of noise, then to me this says that the strong principle of noise is a principle which explains why your computer is indeed unrealistic.
Moving to the other parts of Aram’s third post, I am glad that he is closer to agreeing with me regarding intermediate models, so let me try to check the boundaries of our agreement. Of course, the readers are reminded that in places we agree, and even in places we disagree, we can both be wrong. Aram raised the theoretical question of how to define non-fault-tolerant QC. My conjectures aim to do precisely this, to define boundaries for behavior of QC’s in settings that do not allow FT. Aram asserted that 100 qubits are too few to apply current FT schemes, which raises the interesting practical question of how quantum computers with 100 or fewer qubits will behave.
Here again let me suggest the same conjectures: The errors (i.e., information leaks) for every pair of entangled qubits will be substantially positively correlated, and, for every error correcting code one might try for partial FT, encoded qubits will look like a mixture of a cloud of code words—in addition to standard noise. Thus, errors will systematically depend on the evolution and final state. For such QC’s, trying to create complicated states will lead to error-synchronization, and both correlation and error rate will scale up. Small QC’s demonstrate that the issue is not really scalable quantum computers but universal quantum computers. My conjectures allow quantum computers to scale but predict that their behavior with many qubits will be similar to their behavior with few qubits.
I will express my thanks to Aram for his wonderful partnership in our debate at a later occasion, but let me now thank him especially for his concluding sentence above—about the need for “Eve’s advocates” to push forward challenging theories of noise while the field is still in a young theoretical stage.
Intermezzo by Aram, Before Preskill’s Act
An even more “imaginary” quantum computer sets up a view of the real world that connects to Preskill’s paper, and provides another thought experiment that refutes Gil’s conjectures. Imagine a large quantum computer with a high rate of noise. The experimenter attempts to create entanglement between qubits, and can indeed apply the entangling operations, but this entanglement almost immediately disappears because of noise from the environment. So far uncontroversial.
But what does it mean that the entanglement disappears because of noise? The Schrödinger equation says that the state of the entire universe changes unitarily. How can entanglement disappear in such a model? This is an old problem in the interpretation of quantum mechanics, similar to the measurement problem, but somewhat easier to resolve. The key is a principle commonly called “going to the church of the larger Hilbert space”:
Any noisy quantum process can be modeled as a unitary interaction with the environment, followed by discarding [formally, tracing-out] the qubits of the environment.
That is to say, unitary evolution only appears noisy because it involves systems, such as photons heading away at the speed of light, that are out of our control. This picture offers a way to resolve the problem of noise in quantum computers, albeit one that won’t yield any practical computational speedups. We simply redefine what we call the “computer” to include all of the qubits in the environment that interact with it. This gives us a quantum computer that is definitely in a pure, highly entangled state, performing calculations that we have no idea how to simulate in sub-exponential time.
What does this have to do with Gil’s conjectures? It proves that for them to possibly hold, they will need to distinguish between the qubits we care about in our quantum computer, and the qubits in the environment that we don’t care about, can’t control very precisely, and may not even have a good model for. These are important practical distinctions, but they are not physical ones. I don’t think that anyone would believe in a model of decoherence that applies to qubits we care about, and not qubits that we don’t care about. But this is what Gil’s conjectures need.
Preskill’s Paper and Further Exchanges
John Preskill’s initial comment on the first item in this series picked up the Hilbert-space principle:
Gil says that while he is skeptical of quantum computing he is not skeptical of quantum mechanics. Therefore, I presume he takes for granted that a quantum computer (the “system”) and its environment (the “bath”) can be described by some Hamiltonian, and that the joint evolution of the system and bath is determined by solving the time-dependent Schroedinger equation. If Gil’s conjectures are true, then, no matter how we engineer the system, the Hamiltonian and/or the initial quantum state of the joint system must impose noise correlations that overwhelm fault-tolerant quantum protocols as the system scales up.
Preskill’s paper proves a theorem that establishes general conditions under which such a Hamiltonian allows fault-tolerant quantum computing. It extends to a more general setting a result proved in a 2006 paper of his with Dorit Aharonov and Alexei Kitaev. Preskill noted in the comment that his conditions are not necessary for FTQC, and followup opinion is that their failure would not constitute tangible evidence against FTQC in general.
The same comment already prefigured Kalai’s reaction that such Hamiltonian noise models are not physically realizable, saying “that could well be, though I would like to understand better his reasons for holding that opinion.” In a followup, Preskill noted that his conditions place no burden on the environment except that its qubits can be cooled. While conceding that this may not be realistic, he continued, “It would be helpful if Robert [Alicki] or Gil could exhibit families of Hamiltonians which allow fault-tolerant classical computing but disallow fault-tolerant quantum computing. Such examples would help to clarify where the disagreement lies.” This harks back to the classical/quantum aspect of Aram’s first response.
One point of disagreement later in that thread turns out to be the “freshness” of additional ancilla qubits required by FTQC during its operation. Comments by John Sidles and Aram further down portrayed this and related issues as practical engineering obstacles rather than fundamental physical limitations, and Sidles ended the thread with the point that assessing the latter requires tighter modeling and greater mathematical rigor on both sides, along lines that Preskill’s paper itself exemplifies.
Gil created a long agenda of 25 issues raised for further pursuit, including several related to Preskill’s paper. He later added a 26th issue (thermodynamics) which led to a detailed comment by Dave Bacon, and further discussions.
Gil and Aram began further discussion of the second response here where they were joined by Klas Märkstrom and commenter “matt”, and this may be refined in a further post. The comments by Joe Fitzsimons referenced by Aram above followed. Gil affirmed the Hamiltonian-Schrödinger part of Preskill’s comment, and began replying to the rest, as the discussion continued in that thread.
Getting back to Preskill’s paper, Sidles began considering concrete realizations of FTQC here, where he tied the question of whether Preskill’s conditions can apply in the real world to other open issues in quantum field theories and relations to relativity, and later here with his own skeptical conjecture about ohmic noise. The latter drew a direct reply last week from Preskill, who argued that the conditions in his paper did not entail those in the other John’s conjecture. A ringside commenter asked for general description to understand why “ohm” should be a mantra here.
Finally, Gil opened a reply to Joe Fitzsimons’ attempt to refute his conjectures by considering “blind computation,” and after discussion on its feasibility and general matters, this drew a response from Fitzsimons affirming its nature and citing an experiment. Gil then responded four days ago to queries from Boaz Barak, and that thread is ongoing.
Censorship and Qudits?
Steve Flammia and Aram have also written a note that approaches Gil Kalai’s Conjecture C from an extra-dimensional angle. They reason that the logic behind the conjecture should extend to generalizations of qubits with -many basis states for
, called qudits. Then they demonstrate that such an extended conjecture is violated for
for some states that reasonably comply with the conjecture’s condition that the states be plausibly creatable by experiments. Finally they do so for qubits, with
, arguably remaining within the realm of plausibility. The note has further discussion of these points.
Open Problems
Aram also contributes a remark that “the pessimistic scenario of my previous post actually goes too far. In practice, when errors are correlated, they become easier to correct with techniques like composite pulses, spin echo and decoherence-free subspaces.” In what theoretical scenarios do these methods apply?
What might distinguish an engineering obstacle that cannot be overcome from a theoretical impossibility?
[fixed conflation of commenter “matt” and Matt Leifer; they are !=]
Trackbacks
- Flying dragons of the 3rd millennium? | Are You Shura?
- How Good Is Your I-magination? « Gödel’s Lost Letter and P=NP
- The Quantum Fault-Tolerance Debate Updates | Combinatorics and more
- Quantum Refutations and Reproofs « Gödel’s Lost Letter and P=NP
- Can You Hear the Shape of a Quantum Computer? « Gödel’s Lost Letter and P=NP
- Quantum Repetition « Gödel’s Lost Letter and P=NP
- Quantum Supremacy or Classical Control? « Gödel’s Lost Letter and P=NP
- The Quantum Debate is Over! (and other Updates) | Combinatorics and more
- What Would Be Left, If…? « Gödel’s Lost Letter and P=NP
- My Quantum Debate with Aram II | Combinatorics and more
- My Quantum Debate with Aram III | Combinatorics and more
- Why Is There Something? | Gödel's Lost Letter and P=NP
- Predictions For 2019 | Gödel's Lost Letter and P=NP
- To cheer you up in difficult times 29: Free will, predictability and quantum computers | Combinatorics and more






What might distinguish an engineering obstacle that cannot be overcome from a theoretical impossibility?
The short answer:
Yeah, but can you prove it? 🙂
A somewhat longer answer would be that an engineering obstacle that cannot be overcome (or that overcoming it is hard and we cannot explain why) is a call for a theory that will explain it.
“What might distinguish an engineering obstacle that cannot be overcome from a theoretical impossibility?”
Dear Ken, of course, this is a great question which goes well beyond the present discussion. I do hope people will give also knowledgeable serious answers.
It’s only once we’ve come up with a new theory that we’ll be able to make a distinction. Before Einstein, the failure of the Michelson–Morley experiment was just another engineering obstacle. After him, it became the result of a strong theoretical impossibility.
Is that true? I know the example of a Perpetual Motion Machine may be overused in these discussions, but in that context, the problem of the laws of thermodynamics seems to be essentially theoretical. So it is possible in some contexts to distinguish between engineering issues and theoretical barriers.
Only if you’re aware of thermodynamics, can you make a distinction between the impossibility of perpetual motion and a mere technical obstacle. In view of what we know today, these examples from the past had been unrealisable from eternity. But the people of that time didn’t know the underlying theory and therefore they could argue that perpetual motion was still possible – if not yet achieved. Nobody was able to prove them wrong.
By the way, I can’t see why relativity should be considered less theoretical than thermodynamics… 🙂
So, Aram, regarding your new even-more-imaginary quantum computer. Do you really think it is a good idea to throw the entire universe at my conjectures?
It doesn’t have to be the entire universe. The “qubits” of the computer could be defined to be whichever degrees of freedom interact with our system, or with anything that has interacted with the system. This would be a horribly complicated mess, and probably would expand in all directions at roughly the speed of light.
But like Maxwell’s Demon, it doesn’t have to be a useful piece of technology to be a useful thought experiment.
Aram, but you do need for the thought experiment to enlarge the system to a larger one which is noisless, or, in other words, on which your evolution in unitary, right?
In our own quantum spin microscope experiments, we go to great lengths to make the universe as small in size as possible, and as low in dimension as possible, and as cold as possible, for the engineering reason that we want our device to see as few vacuum modes as possible.
Optically speaking, our devices look much like everyone else’s: we run nine independent interferometers (2×3 for 2-color 3-axis sample position, 2×1 for a calibration axis, one for cantilever motion), and each interferometer’s “universe” is a single-mode 2×2 fiber interferometer with one emission port, two detector ports, and one dark port.
So in effect, our quantum universe by design is very dark, very small, very cold, and very low in space-time dimensionality. Yet even so, it’s a pretty complicated universe, in which a substantial number of far-from-equilibrium quasi-continua “stare” at each other continuously.
The end result, from a fundamental physics point-of-view, is that the irreducible noise in our spin microscopes enters via the photon/phonon/electron quasi-continua that are associated to the diodes and the dark ports. And this is true generically in existing QIT technologies of all varieties.
It would greatly simplify the physics, and substantially reduce noise levels, if we could wholly eliminate quasi-continuum quantum dynamics from our devices … but no-one knows how to achieve this (even in principle, AFAIK). And it would be great if we had robust dynamical theories of the quantum noise mechanisms that are associated to quasi-continua … but at present we understand just enough to have good reason to be dissatisfied with our theoretical understanding of them (as reviewed earlier).
Largely in consequence of these uncertainties — both practical and fundamental— my personal sympathies in this debate have ended up split pretty evenly between Harrowism and Kalaism. As Feynman expressed it:
Therefore, a particularly interesting question, which need not have one single answer, and which hopefully has multiple good answers (that people hopefully will post here on GLL!) is “What comes next?”
And please let me express appreciation and thanks especially to Aram and Gil, and Dick and Ken, and Dave (Bacon) and John (Preskill), and everyone else who has contributed to creatively to this outstanding debate. Thank you all! 🙂
I would like to make it known that I am not commenter “matt”, as suggested by KWRegan in a previous comment thread. My only contribution to the debate so far is a silly joke, so whoever “matt” is deserves to be mentioned in the main post instead of me.
“It will be noisy—in principle!—no matter how much money you throw at it”
Aram gave a detailed scenario, and you have responded with an anecdote. Noise isn’t a problem. What is the physical mechanism that could transmit your strongly correlated noise in this scenario?
Hi Nurit, thanks for the good question.
The quote referred, of course, to million-people concerts like the one in Woodstock, and not to quantum computers. The point is that I don’t think it serves any purpose to schlep (move) the optical quantum computer to a quiet intergalactic space.
The optical wires quantum computers themselves are interesting, and I don’t have an off-hand answer where correlated errors will come in this and similar cases (even when you implement it on Earth), and it is worth further discussion.
Aram, I have an additional question regarding your last thought experiment.
My Conjecture 1 (you can call it the research hypothesis) asserts that in a noisy quantum computer:
(*) When you encode a qubit with n qubits you will get a substantial mixture with unintended code words in addition to standard noise.
The standard assumptions on noisy quantum computers (you can call it the null-hypothesis) asserts
(**) When you encode a qubit with n qubits you will get a mixture of your intended state with standard noise, namely noise which is substantial on every qubit and essentially independent.
Here by “substantial” I roughly mean that the noise level is above a certain constant independent from n, and by “essentially independent” I allow small violations of statistical independence which are obtained by the last rounds of the computation and by small dependence which decay with distances like in John Preskill’s model.
I do not see how your thought experiment can prefer (**) over (*)? Does your thought experiment reject both these descriptions of noisy quantum computers?
The difference between (*) and (**) is that in (*) the universe needs to know what code you are using in order to foil you. This attributes both more intelligence and more malice to the universe than I am willing to believe that it has.
Yet on the other hand, it has happened that elements in mathematics that seemed unnatural and even malicious from an algebraic perspective (like violations of Pythogoras’ theorem) were eventually appreciated as natural from a geometric perspective (like the propagation of wave-fronts on geodesics). So perhaps Gil’s conjectures make better sense from a geometric perspective?
John, I guess you’d like to say that if quantum mechanics is mildly nonlinear then we might only notice this if we build a quantum computer and attempt to create a large-scale entangled state. Discovering this is in a sense the best case for quantum computing, as it would revolutionize physics.
I doubt this for a few reasons. First, I don’t think quantum computing would probe states any more entangled than we already find in nature. The only difference is that the entanglement would be under our control. So any nonlinearity that shows up in a quantum computer with 10^10 qubits should also have shown up in a semiconductor with 10^20 atoms.
Second, if you accept nonlinear evolution, then you also have to throw out the Born rule. And the tensor product is thrown into doubt, or becomes meaningless since we don’t have linearity. At which point all you know about physics is that |psi(t+1)> = f(|psi(t)>) for some function f, and applying measurement M to state |psi> produces output distribution g(M, |psi>) for some function g. I suppose it is just my prejudice that I don’t like theories that are so unconstrained.
Awww … you’ve stepped on my best lines, Aram! And particularly I agree that “this is the best case for quantum computing.” 🙂
As it turns out, Steven Weinberg has expressed an even stronger faith in strictly Euclidean quantum state-spaces, than any so far in this debate:
Yes, if we discover that the state-space of nature is *not* an exactly linear Hilbert space — or even if we discover (as engineers already appreciate) that it is computationally advantageous to regard Nature’s state-space as effectively non-Euclidean — then a great many computational techniques that we presently regard as exact, will come to be regarded as approximations.
But should we regard this as a tragedy? Or is it a wonderful opportunity for an Aaronson-style “great adventure”?
As a test of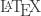 … and also for pure mathematical adventure … let’s consider the concrete non-Hilbert state-space manifold
… and also for pure mathematical adventure … let’s consider the concrete non-Hilbert state-space manifold
which (as it turns out) is a state-space of dimension that is naturally immersed in a Hilbert space
that is naturally immersed in a Hilbert space  (that is, a standard Hilbert state-space of 65,536 qubits).
(that is, a standard Hilbert state-space of 65,536 qubits).
So this state-space has precisely *one* missing dimension. And yet it is not a “slightly nonlinear” state-space … from a geometric point-of-view, it is wildly nonlinear (try calculating its entropic volume, for example).
But is it observably nonlinear? IMHO, questions like this are a great adventure! 🙂
Interesting comments are coming faster than I have time to cope! I’ve got another one by Aram in a reply window, but I probably need to go to bed… Let me say here, though, that I subscribe to the essential linearity of QM, and oddly my chess work has given me an insight into a related issue of how non-monotone effects can arise from monotone ingredients.
Namely, the current form of my model—which generates probabilities p_i of a player represented by certain skill-parameter values choosing the i-th move in any given position—uses values v_i for moves m_i given only at one specific reference depth d of calculation. As such, the model has the monotone property that for all players, the higher v_i, the higher p_i. This flies in the face of the common-sense observation that weaker players often prefer weaker moves.
However, an expanded model in which I use analyses at different depths d to generate probabilities p_{id} promises a natural solution for much of the issue. It adds weights w_d over all relevant depths d as a further skill parameter, perhaps parameterizing them further by the mean m and variance of (say) binomial distribution (possibly skewed). Then the final expression for p_i becomes the positive linear combination
p_i = \sum_d w_d*p_{i,d}.
Higher m means higher skill. The upshot is that a weaker move will often look more attractive at the lowest depths. Weaker players, as modeled with lower m and hence higher w_d at the lower depths, will thus generate a higher probability p_i for that move. This gives a negative effect despite having nothing more than positive linear combinations of expressions from a monotone model.
Is there anything yea-simple as an analogy for the emergence of nonlinear dynamics?
For algebraic geometers, here is a (hopefully) corrected version of a manifold having a natural Segre embedding in a Hilbert space of 65,536 qubits, that is deficient in dimension by precisely unity:
And yes, the secant rank![\left[\tfrac{(2^{2^{16}}-1)}{(1+2^{16})}-1\right]](https://s0.wp.com/latex.php?latex=%5Cleft%5B%5Ctfrac%7B%282%5E%7B2%5E%7B16%7D%7D-1%29%7D%7B%281%2B2%5E%7B16%7D%29%7D-1%5Cright%5D&bg=ffffff&fg=333333&s=0&c=20201002) of this manifold is an integer (albeit, a tremendously large integer). 🙂
of this manifold is an integer (albeit, a tremendously large integer). 🙂
After some numerical experiments (that regrettably are not likely to be done very soon) I hope to post more about quantum trajectories on these quantum state-spaces that are minimally dimension-deficient, yet far-from-flat.
For now, I will close with the cheerful advice of George Dantzig: “In brief, one’s intuition in higher dimensional space is not worth a damn!”
And as Ken knows, this is true equally on large-dimension dynamical state-spaces and large-dimension chess-engine search-spaces! 🙂
It’s one thing to describe a nonlinear state space, but you also have to explain what Hamiltonian evolution looks like (ok, so you pull it back) and what measurement looks like (i.e. what happens to the Born rule?) and how it combines with other systems to form a larger theory (i.e. what is the analogue of a tensor product). I think these sorts of things are what Weinberg was talking about when he said that it was hard to make QM nonlinear.
It’s also hard to talk about experimental evidence before we have any theoretical idea what nonlinear QM might resemble. For example, you might hope that a nonlinear theory of QM will modify linear QM the way that Einstein’s relativity modifies Galilean relativity. But think about how someone might talk about this in the 19th century. Before Maxwell’s equations came along, there was no theoretical clue that anything was wrong with Galilean relativity (just like there’s no hint today that anything is wrong with linear QM). It would be somewhat futile to ask at the time for direct evidence that Galilean relativity was wrong. Instead, we needed the *indirect* evidence of Maxwell’s equations, which told us where to look.
Similarly for quantum mechanics, we have theories of what extra dimensions might look like, and how we can test them, say with precise measurements of gravity at short distances. But we have no plausible nonlinear theories that I know of, nor theoretical clues that we need such theories.
Aram, (projective) measurements and (discrete) noise are pulled-back using standard Lindbladian unravelings — the former being a coarse-grained description of the latter. Carlton Caves has good on-line notes on the details.
The discussion so far is terrific, and upon the physics bones that Gil and Aram have provided, I would like to add some engineering flesh and even some newly-discovered mathematical skin!
For engineering flesh, let us gaze upon a straight-from-the-catalog 2×2 optical coupler, and we will adopt the non-skeptical assumption that this physical coupler (and its -port generalizations) can approximate, to any desired accuracy, any desired unitary transform
-port generalizations) can approximate, to any desired accuracy, any desired unitary transform 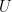 :
:
Then we can distinguish three classes of opinion regarding FTQC, per the summary that follows.
——————
Notice Please let me say in advance that I personally regard all three of the following opinions as reasonable, and consider it fun to embrace them simultaneously, and in any event regard it as being neither necessary, nor desirable, nor feasible, that everyone think alike in these matters. Hence we will regard as nugatory any and all manifestations of what Gauss called “the clamoring of the Boeotians” with respect to FTQC.
——————
FTQC Nonskepticism “It is feasible, both in principle and (eventually) in practice, to couple qubits, photon sources, and photon detectors, via unitary optical couplers (or their functional equivalents), such that quantum computations can be scaled to arbitrarily large systems of qubits.”
This is the doctrine of the 2002 and 2004 QIST Roadmaps (LA-UR-02-6900 and LA-UR-04-1778), which are themselves sufficiently detailed, upon which sufficiently much has been written, that no further comment will be given in regard to them.
——————
Moderate FTQC skepticism “It is not presently known to be feasible — even in principle — to construct photon sources / photon detectors / dark ports (or their functional equivalents) that scalably preserve the unitary evolution of qubits.”
This is the point-of-view (which at present is rather widespread among quantum opticians) that amounts to a humble confession: “We don’t presently possess a solid mathematical or physical understanding of the quantum dynamics that is associated to quasi-continuum state-spaces.”
——————
Radical FTQC skepticism “We can’t be confident that FTQC is feasible because we presently have insufficient grounds to be confident that the Nature’s state-space is a Hilbert space. And probably it isn’t.”
Now, Scott Aaronson has been particularly eloquent in arguing that exploring alternatives to Hilbert-space quantum physics is “the great adventure of our lives.”And Tony Zee has eloquently argued that “formerly cherished concepts will have to be jettisoned.”And Aram Harrow and Steve Flammia have posted their essay “Counterexamples to Gil Kalai’s Conjecture C”(which Dick linked-to).
So let’s embrace all of these ideas simultaneously — since they are individually excellent! — as our point of embarkation upon a skeptical voyage that (hopefully) will be a great adventure.
We adopt from Aram and Steve’s essay a concrete Hilbert state-space . We adopt Scott’s entire confidence in the quantum axioms of Nielsen and Chuang’s Quantum Computation and Quantum Information (henceforth QCQI). We adopt from Carlton Caves’ on-line notes a Lindbladian formulation of the QCQI axioms (which we translate into stochastic differential forms of Stratonovich type). And we know from modern geometric dynamics and thermodynamics that differential forms pullback naturally onto submanifolds.
. We adopt Scott’s entire confidence in the quantum axioms of Nielsen and Chuang’s Quantum Computation and Quantum Information (henceforth QCQI). We adopt from Carlton Caves’ on-line notes a Lindbladian formulation of the QCQI axioms (which we translate into stochastic differential forms of Stratonovich type). And we know from modern geometric dynamics and thermodynamics that differential forms pullback naturally onto submanifolds.
Now we pause, to appreciate that we can pullback the Hamiltonian and Lindbladian dynamical potentials of QCQI, and pullback also the metric and symplectic structures of Hilbert space — that is, the natural Kählerian structures of Hilbert space that locally instantiate “quantum goodness” — onto any submanifold of Aram and Steve’s that we choose.
that we choose.
What submanifolds shall we choose to continue our adventure? What notation shall we embrace? Here Joseph Landsberg’s already-classic “Geometry and the complexity of matrix multiplication” (Bull. AMS, 2008) provides both the submanifolds and the notation.
Notation first (at lightning speed). For vector spaces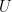 and
and 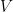 , let
, let  be the familiar outer product. This induces the projectivized Segre embedding, which by definition is
be the familiar outer product. This induces the projectivized Segre embedding, which by definition is  , or equivalently in coordinates,
, or equivalently in coordinates, ![{\text{Seg} \colon [u] \times [w] \rightarrow[u\otimes w]}](https://s0.wp.com/latex.php?latex=%7B%5Ctext%7BSeg%7D+%5Ccolon+%5Bu%5D+%5Ctimes+%5Bw%5D+%5Crightarrow%5Bu%5Cotimes+w%5D%7D&bg=ffffff&fg=000000&s=0&c=20201002) . A common notational shorthand is
. A common notational shorthand is  , and a standard construction is the rank-r secant variety
, and a standard construction is the rank-r secant variety
where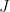 is the natural algebraic join and
is the natural algebraic join and 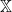 is any algebraic variety.
is any algebraic variety.
Now we are equipped to pullback, in a mathematically natural way, all of the quantum physics of Aram and Steve’s Hilbert space onto any immersed submanifold
Hilbert space onto any immersed submanifold  of that we choose. The following two immersed dynamical manifolds are particularly instructive:
of that we choose. The following two immersed dynamical manifolds are particularly instructive:
It is known that , that is, the manifolds
, that is, the manifolds  and
and  are each of them precisely “one dimension short of a linear Hilbert space.” It is their almost-Hilbert yet essentially nonlinear geometry that makes these manifolds interesting for the analysis of non-Hilbert realizations of FTQC.
are each of them precisely “one dimension short of a linear Hilbert space.” It is their almost-Hilbert yet essentially nonlinear geometry that makes these manifolds interesting for the analysis of non-Hilbert realizations of FTQC.
————–
Aside To the best of my knowledge, it is not known whether , and proofs in this class are generically difficult. For example, that
, and proofs in this class are generically difficult. For example, that  was proved only in 2011 (MR2762993).
was proved only in 2011 (MR2762993).
————–
Thus, radical FTQC skepticism naturally leads to broad class of concrete well-posed questions that includes these:
Heuristically, it is noteworthy that under various mathematical names that include “Kronecker tensors” and “matrix product states”, the application of varieties in every branch of chemistry, physics, biology, and computation has been accelerating at a Moore’s Law pace for the past several decades.
varieties in every branch of chemistry, physics, biology, and computation has been accelerating at a Moore’s Law pace for the past several decades.
So why shouldn’t FTQC participate in this adventure too? 🙂
Conclusion Supposing that one of the 21st century’s Aaronson-style “great adventures” is exploring the radically skeptical thesis that Nature’s state-spaces are varieties of type — we wonder, as dynamically generated by Nature? — then Tony Zee’s class of “formerly cherished concepts that have to be jettisoned” will include the long-cherished ideal of absolute localization in space and time.
type — we wonder, as dynamically generated by Nature? — then Tony Zee’s class of “formerly cherished concepts that have to be jettisoned” will include the long-cherished ideal of absolute localization in space and time.
Needless to say, giving up the cherished physics concept of localization would be a great adventure. Perhaps it is a correct idea, and already we know for certain that it is a mathematically and computationally natural idea that is fruitful of new ideas, proof technologies, theorems, and enterprises.
So let’s continue our still-unfinished yet undeniably great adventure! 🙂
Well, as I feared, not every equation parsed correctly … it was composed using Lucas Trevisan’s (immensely useful) python script ‘LaTeX2WP’, whose translations are good but not always perfect. Hopefully, the main points are evident.
Folks who want to see what Dave Bacon calls “the excruciating details” of almost-Hilbert quantum dynamics can view an on-line PDF version here. Eventually some still-open problems — Does ? What is the lower fidelity bound to approximating arbitrary quantum states in
? What is the lower fidelity bound to approximating arbitrary quantum states in  and
and 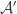 ? — will be posted as questions to MathOverflow.
? — will be posted as questions to MathOverflow.
Thanks again, to everyone, for a great topic!
To the above document have now been added several hyperlinks to the mathematical literature, an assertion from Tony Zee’s Quantum Field Theory in a Nutshell to the effect that “We may have to abandon strict locality [in our theories]” (a quote that somehow I overlooked, but agree with), and a brief discussion of open questions in algebraic geometry that relate to Scott Aaronson’s notion of “sure/Shor separation criteria,”
The tuned-up essay now has a title: Minimal, Moderate, and Radical Skepticism of Fault Tolerant Quantum Computing (FTQC). All this, with a view toward posting next week its open algebraic geometry problems as questions on MathOverflow. Thus, comments from algebraic geometers especially are welcome.
John, it looks like your theory states that Hilbert space should be replaced by a nonlinear subset of the vectors. Assuming you want to keep the Schrodinger equation, then what happens when some Hamiltonian evolution takes you into the forbidden region of excessively-entangled vectors? Any possibility that I can think of leads to nonlinear quantum mechanics, which I believe is toxic, even in small doses.
There seems to be a limitation on the fanciness of LaTeX comments that WordPress understands—when I get time (Dick and I were both traveling these past two days) I will see if I can fix it.
Likewise, moderation seems to come on when your # of comments is congruent to 0 modulo some number q, where q may change nondeterministically…
Aram, the Schroedinger equation on all of these manifolds takes the geometrically canonical form
where is the dynamical flow,
is the dynamical flow,  is the symplectic flow,
is the symplectic flow,  is the exterior derivative, and
is the exterior derivative, and  is the Hamiltonian potential (details here). By virtue of what geometers call “Cartan’s magic formula” (Google it), the resulting dynamical flow is a symplectomorphism, which is geometer-speak for “non-toxic.”
is the Hamiltonian potential (details here). By virtue of what geometers call “Cartan’s magic formula” (Google it), the resulting dynamical flow is a symplectomorphism, which is geometer-speak for “non-toxic.”
The physical intuition is, that for Hamiltonian dynamical flows even on state-space manifolds having grossly nonlinear geometry (think of protein-fold spaces for example) adjacent dynamical trajectories stay “glued together” in phase-space, in such a fashion as to forestall thermodynamical and computational extravagances.
Thus, although some nonlinear state-spaces are computationally “toxic”, others are tonic and even invigorating! 🙂
Given that a huge number of qubits are in superposition during quantum computation, should there be any concern regarding a possibility of orchestrated wave-function collapse, like the one in the model proposed by Prof. Roger Penrose (a more general theory might say how wave-function collapse really happens)? Someday, a quantum computer will have to scale-up to the size of a typical measuring instrument.
A possibly related question is what distinguishes machines built by natural processes from those built or designed by man. We know Nature has built it’s version of a classical computer , what about the possibility of a natural quantum computer?
As an aside, it is interesting that the word “skepticism” has entirely disappeared from this iteration of the Harrow/Kalai debate. It has been replaced by “pessimism”, which is variously described as “extreme” or “dire.”
In this regard, a Google Ngram analysis of “healthy skepticism” versus “extreme pessimism” versus “dire pessimism” is worth considering — healthy skepticism being considerably the most common ngram. And similar usage patterns are evident on the arxiv server, where the use of “skepticism” is prevalent over “pessimism” by 1165 preprints to 370.
Thus, although “skepticism” and “pessimism” both are important roles in STEM enterprises, there is little question as to which role is more popular.
Summary: “Optimistic skepticism” regarding FTQC is not an oxymoron … it may even be among the most enjoyable and productive of mindsets.
Where I see the main weakness of my conjectures
Let me try to explain where I see the main weakness of my conjectures. This is a point which is implicit in Aram’s posts, and clear to experts, but it is useful to make it as clear as possible. My conjectures 1,3,4 are about the nature of noise in noisy quantum computers. My conjectures are about the nature of the overall noise that is expressed in the gap between the intended state of the computer and the noisy state. I think (but we can discuss it separately) that the conjectures give a fairly reasonable description of what Aram calls non-fault-tolerance quantum computers, for example, noisy quantum computers with less than 100 qubits where, according to Aram, we don’t expect fault tolerance by current methods. The question is if these conjectures are reasonable for describing every noisy quantum computer.
Why not to believe that these conjectures hold for quantum computers with many qubits? Let me remind you that when we model quantum computers, standard models of noisy QC’s divide the computation into discrete cycles, between which one can identify “fresh noise” apart from the accumulated effect of previous noise. (Hamiltonian models use continuous time modeling of a similar nature.) The threshold theorem does entail that (when the noise rate is under the threshold) for FTQC to fail, these conjectures must be assumed for the fresh noise. Indeed, the main reason (in my opinion) to be skeptical about my conjectures is that when we model quantum computers we need to assume the statements of these conjectures for the fresh noise. (Again, this applies both to the discrete models and the continuous Hamiltonian models of noise.) While the conjectures for the overall noise seem believable for several scenarios, the requirements for the fresh noise seem unreasonable and counterintuitive.
The models that support this assumptions are much crazier than the standard models or even the more general model discussed by John Preskill. My papers present both discrete modeling in terms of conditions on the fresh noise, and proposes also a Hamiltonian description. Assuming the statements of conjectures 3 and 4 for the fresh noise, which is what I need to assume, amounts to some nonlinear relation between the state and the fresh noise, and gives the impression that linearity of quantum mechanics is violated (although this is not the case), and it is difficult to imagine what is the physical mechanism that leads to such assumption to be satisfied.
This difficulty in relevant especially to Aram’s second post and it supports Aram’s overall concern regarding correlated noise. (As I said, I disagree with Aram’s specific critique regarding linearity of quantum mechanics and I did not regard Aram’s comments about shadow qubits as damaging to my conjectures.) Overall, I see this difficulty as the main issue, and the classical fault tolerance test (Aram’s post 1) as another crucial matter.
One entry point into a substantial physics literature that is associated to Gil’s physical intuition is Crispino, Higuchi, and Matsas’s survey “The Unruh effect and its applications” (2007).
For quantum computing, the associated intuition is that we cannot physically move mirrors, tune interferometers, or change the voltage bias of photon emittors/detectors — or indeed dynamically alter the physical parameters of a quantum computer in any way whatsoever — without thereby altering the parameters of the vacuum (more generally, the quasi-continuum of states) in which the qubits are immersed.
Are there physical effects associated to altering vacuum parameters? Yes, just as with altering any other parameter of a Hamiltonian dynamical system. Are these vacuum dynamical effects nontrivial to calculate and control? Yes, definitely. So is it reasonable to wonder whether these effects might adversely impact the high-order quantum entanglements that are associated to scalable FTQC? Well … it seems entirely reasonable to me! Because in our QSE lab’s experiments, we commonly observe very substantial dynamical effects that are associated to (for example) cavity-length tuning in our interferometers.
Under real-world circumstances, it can happen that beams of light induce a mechanical rigidity (or conversely, instability) that is substantially greater than an equivalent bar of solid diamond. So for us (as for most quantum experimenters) the parameters of the vacuum most definitely have to be carefully designed, and dynamically controlled, in the course of an experiment.
Martin Gardner was fond of a story told of Niels Bohr:
A minimally crazy theory that might possibly support the Kalai conjectures is suggested by two sobering realities:
• Physically, no one knows how to decouple qubits from quasi-continuum baths that are far from thermal equilibrium (and yes, the physics of these baths encompasses the dynamical generation of “shadow qubits”).
• Mathematically, there is no consensus as to how to calculate the dynamical evolution of far-from-equilibrium open quantum systems in the quasi-ohmic limit.
Therefore, until such time as we experimentally demonstrate practical ways to isolate qubits better than we can at present (topological protection being one such path), and we also construct more powerful tools in mathematical physics for analyzing the quantum evolution of such quasi-continuous quantum systems (as the quantum optics folks are doing), we cannot assert with confidence that (in Feynman’s phrase) “it’s obvious that there’s no real problem.”
But is this skeptical point of view crazy enough? Is it crazy enough to stimulate exciting new science, technology, engineering, and mathematics?
From a systems engineering point of view, it would be both shameful and an irretrievable tragedy, should it come to pass that in the 20th century, humanity conceived the beautifully crazy idea of quantum computing, but then in the 21st century, faltered in conceiving productively crazy paths for developing that idea. Because in the words of Malin Craig: “Time is the only thing that may be irrevocably lost.”
Various sobering circumstances are pressing our planet of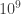 persons sufficiently hard, that we require as many productively crazy ideas as we can conceive, and we require them soon. Gil Kalai’s conjectures and Aram’s critiques are providing us with a mighty good start, that receives this appreciation, and for which Gil and Aram (and John P. and Dick and Ken too) deserve our thanks.
persons sufficiently hard, that we require as many productively crazy ideas as we can conceive, and we require them soon. Gil Kalai’s conjectures and Aram’s critiques are providing us with a mighty good start, that receives this appreciation, and for which Gil and Aram (and John P. and Dick and Ken too) deserve our thanks.
John writes:
Can you explain more why you think this? Photons are pretty well decoupled. So are nuclear spins in many cases. Here was an experiment observing T2 of *seconds* in electron spins in silicon. Ions easily last for milliseconds.
The problem is that it’s hard to do this at the same time as many other experimental feats, like creating entanglement. But decoupling by itself seems extremely doable.
Aram, I have a reply in-queue (relating to the Unruh effect) that references some of this literature. But for your specific examples, its been known for more than 50 years nuclear spins can have a very long provided that no apparatus is looking at them.
provided that no apparatus is looking at them.
So this is yet another instance in which coupling of a quasi-continuum to qubits induces non-trivial dynamics.
Perhaps we might couple different vacua to our quibits during the course experiment, some vacua dissipative, other vacua not? To me, the QIT of vacuum-switching is plausibly nontrivial.
In the above, the phrase “no apparatus is looking at them” is a hyperlink to Bloembergen and Pound “Radiation damping in magnetic resonance experiments” (Phys Rev 95(8), 1955).
In my thought experiment nothing is mixed, because I will redefine the system to include everything the computer touches. And nothing is undesired, because I am an easy-going fellow who simply desires the exact state that the Hamiltonian of the system gives me.
My thought experiment avoids both of these. My point is that in some cases, noise or a trembling hand keeps us from achieving our desired state, but this can be fixed either by changing the noise or by changing our choice of desired state. And it is very hard to build a sensible theory in which physics depends on the desires of the experimentalist.
Aram, doesn’t your thought experiment allow perpetual motion machines? 🙂
They allow perpetual motion like that of the electron around a nucleus. Ok, it’s not really orbiting, but hopefully this gives the picture.
My model of dynamics (not really due to me…) is that after time t, state |psi> becomes e^{-i H t} |psi>, where H is the Hamiltonian of the universe (or whatever bounding box we can put on the system). So in a sense, yes, |psi> is forever changing, assuming it’s not an eigenvector of H.
Usually, though, when people say perpetual motion, they mean perpetually doing work, which is a thermodynamic idea. Nothing about “my” model would imply this.
Aram, Just to understand the details of your suggestion. You wrote: “In my thought experiment nothing is mixed, because I will redefine the system to include everything the computer touches”, do you need to redefine the computer so that .it include also everything the computer toaches, and everything that touches everything the computer touches and so on so that the entire evolution on the redefine computer will be pure? (Or perhaps you don’t care that the added qubits themselves will be mixed.)
The analogy between quantum computers and universal James Bond cars.
While we are discussing Aram’s interesting thought experiments, I would like to raise again my thought experiment from my short rejoiner to Aram’s second post. In this thought experiment I asked you to imagine a quantum mechanical world where in order to prepare or emulate a quantum state (or a quantum evolution) you need to create a special machine. Each type of state requires a different type of machine.
Of course, there are many cases in history where certain machines like the submarine, the parachute, and the airplane were anticipated hundreds of years before they where actually built, but the idea of one machine that can serve as an airplane, a submarine and a parachute, seems less common. One example, in this direction, is the James Bond car.
The James Bond car is a collective name for a series of remarkable general-purpose cars, created by Q (Major Boothroyd) for Agent James Bond (007) in the James Bond movies. Can we have a universal James-Bond car? And is a universal James Bond car (or a universal machine) a better analogy for quantum computers compared to the common analogy with universal computing devices like digital computers (or perhaps, the human brain)? For the analogy with James-Bond cars we can forget about the computational purposes of quantum computers and think about them as machines that create complicated quantum evolutions and states.
The idea that emulating each type of quantum evolution and quantum state requires special-purpose machine has bearing on several issues in this discussion. For example, Aram described an interesting while complicated scenario of how the enviroment “remember” the computation via shadow qubits. But, of course, if the intended evolution requires a special device then the environment (namely this device) “remembers” the entire intended evolution, and the description of the type of feasible approximations to pure-state evolutions and related Hamiltonian models may rely on that “memory”.
Most models of FTQC that people talk about are almost James-Bond style, in if one were built for a special purpose (saying factoring a specific number), it wouldn’t be much more work to have it run an arbitrary quantum algorithm. Joe’s work on blind quantum computing somewhat expresses why this is true. Here’s the idea.
In FTQC, we have to constantly measure error syndromes, do some simple classical processing, and based on that, apply some Pauli corrections (i.e. products of single-qubit gates). Gates also require this measure-and-correct strategy. So by changing the corrections we already have to apply, we can perform different gates. And of course, you can construct a fixed order of gates and construct essentially any circuit from them by selectively deleting some (which is what we can do by changing our Pauli corrections).
But this is the type of distinction that is hard to make “in principle” because if you have a recipe for building a quantum computer, you could always imagine a classical robot that carries this out. Then the entire system is a universal quantum computer.
I thought that this is obvious but perhaps I should explain that a universal James Bond car cannot really be built (in principle!). Even the cars Q built in the Janes Bond movies stretched the imagination, and those were machines capable of only few different purposes. When you try to impose too many purposes on the same machine you will get contradictory constraints.
(If you assume that you can build a universal James Bond car then probably you can build also an advanced model of a blind James Bond car where James, sitting in the car as the rest of the universe does not know if the machine is an airplane and he is a pilot, or the machine is a submarine and he is a sailor, or the machine is a toaster and he is a toast.)
But I write this message on a universal (classical) computer. It’s even running several different programs *simultaneously*.
Dear Aram, this is the crux of the matter: If quantum computers are analogous to digital computers (that can be built) or to a universal James Bond car (that cannot be built).
One more thing. Gil and I were emailing privately about what I meant by “addressability” but probably I should clarify that here.
Basically the idea is that one problem with many quantum computing implementations is that single-qubit rotations are done with indiscriminate laser or RF pulses that address all qubits simultaneously. Often frequency can be used to select particular atoms, but this scales to O(1) different types of qubits that can be addressed. One approach to this it to use a cellular-automaton model of a quantum computer. This can give universal quantum computation, but with nasty (polynomial) overheads, and a much worse threshold (and to make them fault-tolerant, the demands on the “O(1)” get worse.)
Room temperature (liquid) NMR has another addressability issue, which is that a sample will contain n molecules, each with k atoms, and this effectively means n copies of a k-qubit quantum computer, each responding to the same pulses and producing the same signal. This is unfortunate because n ~ 10^{20} and k is usually more like 2 or 5 or 10. if we could address molecules individually, we could do much more, but of course this is not realistic.
In these systems, decoherence times can be extremely long, like milliseconds or seconds. So they form a nice example of how quantum computing can be derailed for reasons unrelated to errors.
Of course, a skeptic might say that as we add more control lines, we inevitably introduce more noise. But this is a thin reed to stand on, in part because of the cellular-automata examples.
Aram, regarding intermediate models, you asked: “what we can do with 100 qubits that experience a noise rate of 5% per gate”, do you agree that Conjectures 1,3,4 give reasonable predictions for this case?
I think I agree only if you don’t do any error correction.
If you have 100 noisy qubits, you could use them to encode 1 logical qubit in a 49-qubit code (that’s a [[7,1,3]]-code (1 logical qubit, 7 physical qubits, distance 3) concatenated with itself), and you could use the rest for ancillas to help with error-correcting it.
So then you’d have low noise (of course, it’s another constant, just lower than 5%), which you might consider contradictory to the conjectures.
Of course in this case, all you get is one logical qubit, so that’s kind of disappointing. But your conjectures don’t care about how efficient the FTQC scheme is, as long as it’s polynomial, right?
That’s interesting.
Right, my conjectures don’t care at all about the efficiency of the FTQC scheme.
Let me ask a simpler question. Let’s consider quatum computers where the error rate is 8%.
We still can try to implement the [7-1-3]-code or any other code but we dont know how to do it in a fault-tolerant way; it is well above the threshold of the most optimistic FT schemes. Would you agree that my conjectures give a reasonable prediction in this case?
(For the case we discussed above I would expect under reasonable and completely standard assumptions on the noise, that if we encode a single qubit using 49 others, as you described, my conjectures will hold simply because we dont have enough qubits for FT. Under realistic noise assumptions for such a case I would expect that the “protected” qubit will behave much worse compared to the physical qubits.)
Aram’s second thoght experiment.
Let me make a few comments about Aram’s second thought experiment. Aram’s example is not really related to my Conjectures 1,3,4 since my conjectures are explicitely about noisy quantum computers. Aram’s experiment does not distinguish between the standard noise and my non standard noise so I don’t see how it can be relevant to the my research hypothesis that my noise assumptions are realistic while the standard noise assumptions are not.
Still Aram’s example and the little discussion about it (This is the link to Aram’s last comment about it) raise some good points.
1) “It is very hard to build a sensible theory in which physics depends on the desires of the experimentalist.”
Actually in my conjectures physics does not really depend on the desires of the experimentalist. Conjecture 1, for example, tells you what kind of mixed states you can get when you encode a single qubit using an error correcting code. (In a noisy quantum computer.) It has nothing to do with your intentions. The conjecture implies that if you intend to get something useful for quantum computing, then you won’t get it, and if you are an “easy going fellow” and don’t care what you get, then you will not get anything useful for quantum computing either.
2) Aram’s specific idea to include in the computer “everything relevant” to the qubits we care about (but not the entire universe).
This is a nice idea, and if it works it contradicts Conjecture 2. (So I doubt that it works.) My initial understanding of Aram’s suggestion was that Aram proposes to add to the set A of qubits of the computer, all the rest of the universe, and get a perfectly noiseless quantum computer of some sort.
As it turned out Aram offers something less drastic: to add to A the set B of all the qubits in the neighborhood that interact (even slightly) with A so that the evolution on A becomes essentially noiseless, or as Aram put it: “This gives us a quantum computer that is definitely in a pure, highly entangled state.” I suppose that Aram does not claim (please correct me if I am wrong) that the joint evolution on A union B is pure; Indeed the qubits of B may interact with other qubits in their neighborhood and be very noisy. But Aram claims that the evolution on A is a noiseless highly entangled hidden fragment of the noisy evolution in A union B. This claim does contradict Conjecture 2. Is it true?
3) The sentiment that noise is not a matter of fundamental importance but some technical nuisanse.
This was expressed by Chris in the first post, by Scott on several occasions and here by Aram. Putting aside the universal quantum computer feasibility question, I think that this sentiment is misguided.
Gil says
But who is to say what is “useful for quantum computing”?
The only definition I know is “efficiently classically simulatable” and certainly that does not apply to QM, even when there are no error-correcting codes in sight.
That’s the point of being “easy going” about it. I define the quantum computation to be whatever the system does. For example, maybe I *want* to know what happens when a textbook quantum algorithm, like Shor’s, is run in the presence of a 10% noise rate, and with no error correction. Who’s to tell me that this isn’t what I want? Then the noisy quantum computer will give me the answer *exactly* just because I’ve defined the answer to be the output of the noisy quantum computer.
I claim this *is* useful for quantum computing, at least with a tortured definition of what quantum computing is. But despite this definition being contrived, I don’t see any refutation of it. Without a known classical simulation, it’s definitely not classical computing. Sure, it’s not general-purpose quantum computing, but you only need one example of quantum computing being possible to falsify your conjectures.
Thinking about this more, it is pretty hard to make my second thought experiment work without something drastic like bringing in the entire universe. The difficulty is that the qubits at the boundary will in general be mixed, or equivalently, entangled with other, farther away, qubits.
Here is how I might try to rescue it. We want to keep the quantum computer from being ridiculously large. Suppose we instead make the experimentalist’s knowledge ridiculously large. For example, we might suppose the experimentalist knows the wavefunction of the entire universe. Then the state of the quantum computer could be approximated to high accuracy by using this knowledge to selectively disregard many qubits. As before, this doesn’t have to be realistic, because a decoherence model shouldn’t depend on the experimentalist’s knowledge, no matter how realistic.
To keep the knowledge a little smaller, we need an approximately contained system. Certainly, many spin systems stay contained for a long time. But let’s think a little more ambitiously. Let’s use a block of some semiconductor (our noisy quantum computer), surrounded by some vacuum, surrounded by a metal sphere, surrounded by vacuum, surrounded by another metal sphere, and so on, several times. Certainly some things will couple to the system and carry information away, like neutrinos, and even photons if they work hard enough. But the system will still be approximately isolated for long enough for some interesting computations.
Aram, the system of concentric metal shells that you have described is an off-the-shelf commercial product that is known to cryogenic engineers as “superinsulation“, for the counterintuitive reason that heat generated within the innermost metallized sphere can’t get out! Even a classical computer chip will burn up within seconds if it is so insulated.
Well, it contains its own power in a battery, so there’s a limit on how hot it can get.
But I don’t need this thing to compute Shor’s algorithm. I only need it to compute e^{-iHt} on itself, and a few of the inner-most shells. This computation is probably uninteresting to most people. I would say its main application is conceptual.
I forgot one more assumption: the outside observer should know the pure state that the system starts in.
Hi Aram,
Rather than increasing the size of the computer as you go, can’t you do the something similar in reverse?
Suppose you run the evolution of the system for time T, and consider the output the state of some fixed spherical region of the system of radius R. This defines a particle horizon at time 0, outside which nothing can possibly influence the state of your output system at time T, which (assuming we are in flat space) has a radius of R+cT, where c is the speed of light. Now, if you assume that the subsystems interacting within this region have a roughly constant density. Then the number of orthogonal dimensions within a region of volume V is $\exp(KV)$, where K is some constant corresponding to the density of subsystems and their local dimension.
The number of dimensions of the total subsystem within the particle horizon, but outside the output region (which I will refer to as the boundary region) is then $D_E = \exp(\frac{4}{3}\pi K ((R+cT)^3 – R^3)) = \exp(\frac{4}{3}\pi K ((3R^2cT + 3 R c^2 T^2 + c^3 T^3))$, while the output region has $D_O = exp(\frac{4}{3}\pi K R^3)$ dimensions. Now, if choose R such that it is polynomially bigger than cT, say $R=c^2 T^2$, then $\log(D_E)$ grows exponentially in $T^5$ where as $\log(D_O)$ grows as $T^6$.
Assuming the output system starts out in a pure state, by time T it can only have become entangled with particles within the environment region. However, the dimensionality of the output system is an exponentially small fraction of the dimensionality of the output system, which limits the amount of entanglement, so that the number of ebits scales inversely in T as a fraction of the total number of qubits contained in the output system. Thus, by monogamy of entanglement, the output region must be very close to being in a pure state.
Aram, my broader point was that every FTQC embodiment (known to me) is continually “stared at” by FT circuits that contain far-from-equilibrium reservoirs as essential elements … reservoirs that (necessarily) generate heat.
John says:
Well, for my second thought experiment, we don’t attempt to make things FT. Alternatively, we could consider the measuring apparatus to be part of the system. The sole point of this thought experiment is to argue that “the intended state of the system” is an ill-defined concept.
For the more mainstream question of noise in FTQC, yes, measurement introduces noise, not only because of the uncertainty principle but because of the reason you mention. But this isn’t something that people haven’t extensively studied. It’s practically the main thing that ion trappers think about. It’s what stops D-Wave from doing fast gates. It’s definitely in all the error models. And there are of course cases where this noise is essentially non-existent. If I have a KLM-style photonic quantum computer, then one photon detector is not going to cause much damage to the other photons.
But isn’t noise coupling among photons inevitable, as soon as one couples (1) high-efficiency single-photon detectors, to (2) high-efficiency single-photon sources, via (3) low-loss couplers?
Because it is precisely in this FTQC scaling-compatible limit that the quantum currents in the quasi-continuum reservoirs of the detectors, sources, and couplers become perfectly correlated (via Maxwell’s equations of course). Moreover, at least one of these reservoirs (the photon source) has a temperature , and so is far-from-thermal-equilibrium.
, and so is far-from-thermal-equilibrium.
Thus, as soon as we make the photon physics scalable, even purely photonic FTQC models require quasi-continuum quantum reservoirs that are far-from-thermal-equlibrium to continuously “stare” at one another, such that analyzing the physics of the photonic noise, in the FTQC scaling regime, becomes similarly challenging to analyzing the physics of photonic computations.
To express the same point in a more familiar way, the Feynman Lectures on Physics describes the quantum physics of two-slit photon experiments, Stern-Gerlach experiments, Hanbury-Brown and Twiss experiments (etc.) as simple processes.
It’s not easy (for students especially) to appreciate that a typically Feynmanesque pedagogic prestidigitation has been performed: the particle detection process in all three cases is incredibly inefficient. And this quantum inefficiency is not incidental, but rather is essential to Feynman’s pedagogic goal of keeping the quantum physics as simple as possible. Specifically, the trick that Feynman employs (but to the best of my knowledge, never discusses) is the inefficiency of these experiments serves to decouple the dynamics of particle emission processes from the dynamics of particle absorption processes.
Nowadays we appreciate that the quantum physics that is associated to the FTQC objectives of the QIST Roadmap — the objectives that are proving so much harder to achieve than was foreseen a decade ago — is not the simplified-but-regrettably-nonscalable subset of quantum physics that the Feynman Lectures teaches — or even that Nielsen and Chuang’s Quantum Computation and Quantum Information teaches — but rather is a far richer, deeper, and intrinsically more dynamical physics, that (it seems to me) we are pretty far from understanding.
That is why the Kalai/Harrow debate is enjoyable nontrivial: it unites so many beautiful and still-unexplored mathematical, scientific, and engineering topics that have the first magnitude of importance for our 21st century.
Peter Shor: “The difference between (*) and (**) is that in (*) the universe needs to know what code you are using in order to foil you. This attributes both more intelligence and more malice to the universe than I am willing to believe that it has.”
Dear Peter, this is true if you assume that you have a machine that can create the code to your liking and hide it from the universe. This is not true, if you need different machines in order to use different codes.
(Sorry for the typos in my previous comment.)
Dear Gil,
You say “This is not true, if you need different machines in order to use different codes.” For classical computers we know that a single physical machine suffices thanks to the existence of universal logical gates, like the NAND gate. Does your comments about the need for different physical machines mean that you do not believe that it is possible to build any of the different known universal quantum gates?
Hi Klas, this is a good question.
“For classical computers we know that a single physical machine suffices thanks to the existence of universal logical gates, like the NAND gate.”
Right. And essentially we can realize these gates noiselessly and on noiseless bits. We discussed it at length on Aram’s first post. Both Aram and I think that the repetition code is a key for this possibility, and my thinking of the matter is that this is possible by the repetition code even in a noisy quantum world that satisfies Conjecture 1.
“Does your comments about the need for different physical machines mean that you do not believe that it is possible to build any of the different known universal quantum gates?”
For the traditional qubits/gates/FTQC architecture, I don’t think the gates are the problem. The gates we build are (fundamentally) imperfect and there are various other sources of errors when we have a controlled quantum system. So the issue is not of building such gates but of controlling the device and correcting errors. At the end the question is what is a realistic model for noisy quantum computers. If you ask about universal gates on essentially noiseless qubits based on physics gadgets similar to the classic one (e.g. non abelian anyons), then Conjecture 1 may conflict with this idea. This was one of the open problems in my initial post.
In any case, Peter’s distinction between (*) and (**) was already based (at least partially) on a reality of quantum computers. What we see today (e.g. look at this comment by Matt http://rjlipton.wordpress.com/2012/02/06/flying-machines-of-the-21st-century/#comment-18306) is that creating different states requires very delicate special purpose devices.
Just to clarify, I *don’t* believe that the repetition code is essential for classical computing.
I think it makes classical computers way easier to build, but that classical computers could be built without it. The difficulty would be almost as high as that of building quantum computers, but it should be possible in principle for the same reasons.
Well, I think history already shows that the repetition code is not essential, on the contrary it was too inefficient. As I recall it, Richard Hamming invented the Hamming codes, for error correcting, because he wanted to be able to correct errors on weekend runs on the computer he was using, this was in the late 40’s. This could not be done using a repetition code, since it needed too many bits, but by replacing the repetition code with a Hamming code he got both error detection and correcting with the available number of bits.
This was all a matter of being at the right end of 7-10 bit interval so the numbers are not far from current qubit counts.
I meant that classical computers use the repetition code in a way that people usually don’t talk about: using many electrons per transistor is itself a form of repetition code.
In a sense, putting a Hamming code on top of the bits we construct out of bistable flip-flops is like making a concatenated code.
Gil,
“So the issue is not of building such gates but of controlling the device and correcting errors. ”
But, given that the error correcting codes are really just applications of a few gates to the input qubits, shouldn’t we be able to to all the error detection and correction by using only a network of one of the universal quantum gates as well?
If that is the case it seems to me that the conjectures should really boil down to some specific claims about the errors that will appear when we implement this particular gate.
It seems to me that with Kitaev’s “magic states” and computation by teleportation, it might be possible to show that you can do quantum computation solely using qubits which have never seen each other before (in some sense). I don’t know if this will convince Gil Kalai or not, and I also don’t know whether it’s actually possible.
As I parse Gil’s intuitions, one of them is the question of whether there exist, within strictly orthodox QM, uncertainty/duality/reciprocity relations, that act to obstruct scalable quantum computing.
One such uncertainty/duality/reciprocity principle might be: “As noise dynamics becomes more nearly Markovian in time and localized in space, so that error-correction is simple, the quantum entanglement of qubits with quasi-continuum states in the thermalizing noise reservoir necessarily becomes larger, in a dual relationship in which noise determines the reservoir entanglement, and vice-versa.”
Such uncertainty/duality/reciprocity relations definitely have a respectable mathematical pedigree (Terry Tao’s column The uncertainty principle is a recent survey).
But of course, this question is open. In fact, there are so many open questions with regard to FTQC, that the present status of minimal, moderate, and radical FTQC skepticism is in all respects unsatisfactory.
(1) A minimally skeptical point-of-view — that to me seems overly sanguine — is that we already understand these uncertainty/duality/reciprocity mechanisms well enough that (in Feynman’s phrase) “We’re sure there’s no problem.” Here Scott Aaronson is correct (IMHO) to assert that associated to such beliefs is a “burden of proof” that the minimal skeptics have not met yet.
(2) A moderately skeptical point-of-view — that to me seems unduly pessimistic — is that uncertainty/duality/reciprocity relations in orthodox QM likely *are* a serious obstruction to FTQC. Again, Scott Aaronson is correct (IMHO) to assert that associated to this belief is a “burden of proof” that the moderate skeptics have not met yet.
(3) A radically skeptical point-of-view — that to me seems unduly optimistic — is that the state-space of nature simply does not encompass the dynamical trajectories of FTQC. Yet again, Scott Aaronson is correct (IMHO) to assert that associated to this belief is a “burden of proof” that the radical skeptics have not met yet.
So perhaps it is prudent to follow Bohr’s example, by faithfully embracing each point-of-view in turn, for two days out of six, and then on the Sabbath, pray for illumination! 🙂
For Ref
[1] http://www.stanford.edu/class/ee104/shannonpaper.pdf
[2] http://www.ams.org/samplings/feature-column/fcarc-quantum-two
[3] http://arxiv.org/pdf/0910.1396.pdf
[4] http://arxiv.org/pdf/quant-ph/0611157.pdf
Some thoughts for additional exploration. Above are related refs.
We would like to assume that environmental noise can be modeled as a poisson process such that in some Q-qubit computer the qubits are effectively measured by the environment in some random sequence with some half-life. We know that for real quantum systems, this assumption is not always true (via entanglement sudden death or ESD) [3]. ESD appears to be a function of the initial probability of being in an pure state (concurrence).
It is indicated in [3] that when measure K (the probability of initially being pure) is below 0.3 that the system returns to the domain where it can be reliably modeled as a poisson process, which would apparently be more amicable for QECC.
Also, in [4] we learn that partially mixed quantum computers can be more powerful than classical computers.
If we follow along with ref [2] it would seem that an appropriate mental model for the effects of noise is to think of random measurements of qubits by the environment which place qubits into definite uncorrelated states prior to gate operations. Computation that occurs due to gate operations is essentially instantaneous, so its a question of how many meaningful gate operations can be performed before complete state space collapse.
In essence, the problem is that we do not have a theory of quantum computation in the presence of noise analogous to ref [1]. I think it reasonable to expect that a noise free Q-qubit system is unrealistic in practice since sudden death appears to be guaranteed. The problem in that case is trying to complete gate operations within the sudden death time. It is not clear though how the system would respond if it was brought to high velocity. Presumably if one could accelerate the computer to a high relativistic speeds, one might prepare gate operations at low relativistic speeds such that their actions might appear to occur very rapidly in the accelerated system before decoherence occurred.
However, the better question to be asking might be what are the bounds on our ability to produce and utilize mixed quantum systems for useful computation in the presence of noise.
Hmmm … to make the above point in a mathematically constructive way, that explicitly emphasizes the vital role that dualities play in balancing minimal, moderate, and radical skepticism (a stratagem that is borrowed directly from Terry Tao’s essay The uncertainty principle), here is a chart listing six dualizing isomorphisms that enter into a linked chain of analysis that begins with fundamental Hamiltonian potentials (in which the notion of “space” may not enter enter even as a parameter) and ends with the nuts-and-volts of practical engineering hardware.
Physically speaking, these dualities have been known for forty-five years and more, and so there is nothing particularly novel in them. Nonetheless, their unifying mathematical similarity and naturality are not commonly emphasized to students (hence Terry Tao’s essay), and this unity helps too in dissolving boundaries between minimal, moderate, and radical FTQC skepticism that are (in my view) mathematically non-natural, and hence of little benefit to students or to the overall STEM enterprise.
Reply to John Preskill
Sorry for being behind on several important issues and comments addressed to me already from the first post. (I had a variety of conflicting tasks in the first half of February, but, in hindsight, it was good to mainly listen at that early stage of the discussion. Also, it takes me time to digest the comments and think about them, and sometimes I don’t have a reply at all.) I will try to make up for the delay and let me first relate (in two parts) to some important points by John Preskill which are also highlighted in the present post.
(John Preskill:) “I have also found Gil Kalai’s skepticism stimulating, and I enjoyed our discussions during Gil’s visit to Caltech last year.”
Dear John, thanks; I also enjoyed both the visit and our discussions. (I hope you still hang around here in this discussion.)
John’s first comment.
(John:) “Gil’s visit provided the impetus for me to work out some sufficient conditions for scalable quantum computing, something I had been meaning to do anyway. … In any case, Gil believes that Hamiltonian noise models like the one discussed in my notes are not physically realizable; that could well be, though I would like to understand better his reasons for holding that opinion. … And it is a big leap from there to the statement that large-scale quantum computing is impossible.”
I overall agree with what John says. The standard Hamiltonian modeling of quantum computers is very reasonable. The problem is with its consequences which are questionable. (I tend to think that the consequences are even unreasonable, but I firmly believe that these spectacular consequences should be questioned.) This means that we need to examine noise models which seem a priori less reasonable, and this is what my work is about. In other words, we start with the statement that large-scale quantum computing is not possible and we try to study noise models that support this statement.
However, my conjectures have also a related but different purpose. They try to define and model what Aram refers to in the post as “non-FT quantum computers”. Trying to understand how to define and to model non fault-tolerance quantum computers is important for various purposes even if you believe that quantum fault-tolerance is possible. In particular, it is important for understanding quantum processes for which we cannot expect fault-tolerance.
(John:) “Skepticism about the feasibility of fault-tolerant quantum computing is reasonable, and welcome;… Gil’s conjectures also highlight the importance of attaining firm experimental evidence for quasiparticles obeying nonabelian statistics in laboratory systems, since quantum states supporting anyons are highly entangled many-particle states similar to the code states of quantum error-correcting codes.”
I completely agree.
(John:) “(This is my foray into Open Science, in homage to Michael Nielsen.)”
(We should pursue ideas related to “Open Science” also with some skepticism and with a large dose of self-criticism.)
Mathematics and intuition
In response to some critique on FTQC by Robert Alicki John Preskill wrote.
(John:) “It is useful to formulate the question mathematically. Then we can focus our attention on which assumptions in the mathematical arguments ought to be questioned.”
This is an important point. I remember John mentioning to me in Pasadena an advice to physicists by Steve Weinberg (John’s Ph. D advisor, if I am not wrong) to prefer what the mathematics tells on their intuition. (Being a mathematician this advice sounded appealing to me.) This point has a flip side though. If John expects skeptical physicists to give priority to mathematics over their intuition, he may consider a careful study of new mathematical models even if they look intuitively strange.
Hi Gil,
One of your lines in the above has me confused. You say “The problem is with its consequences which are questionable. (I tend to think that the consequences are even unreasonable, but I firmly believe that these spectacular consequences should be questioned.)”
I’m not quite sure from reading this whether you are suggesting that you do not necessarily accept that all physical interactions can be described by a suitable set of Hamiltonians? Is this really the case?
Certainly it is possible to postulate noise models which cannot be written in such form, but such models would be entirely unphysical.
Hi Joe, Yes, of course, I only consider Hamiltonian interactions.
When I said: “The standard Hamiltonian modeling of quantum computers is very reasonable. The problem is…” I meant, of course, that we should reconsider the standard Hamiltonian models. As a matter of fact, as far as I can see, mathematically speaking, my suggested smoothed Lindblad evolution is a Hamiltonian model.
Hi Gil, thanks for the clarification. I guess I read to much into that statement. Can I further ask whether or not you think it is reasonable to restrict attention to 2-local Hamiltonians? The reason I ask is that this has a significant affect on how correlations can arise, since environmental systems must couple separately to different local systems within the computer. This certainly simplifies the fault-tolerance problem, but has strong physical motivation.
Gil, it seems to me that your point-of-view is prevailing in this debate.
Because another point of clarification is that the dynamical flow that is associated to an -local zero-mean Hamiltonian
-local zero-mean Hamiltonian 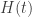 is geometrically very different from the dynamical flow that is associated to a zero-mean Lindbladian process
is geometrically very different from the dynamical flow that is associated to a zero-mean Lindbladian process  . Both flows are predicted by orthodox QM, but the former flow is a zero-mean symplectomorphism, while the latter flow is neither zero-mean nor a symplectomorphic.
. Both flows are predicted by orthodox QM, but the former flow is a zero-mean symplectomorphism, while the latter flow is neither zero-mean nor a symplectomorphic.
In consequence, for -local
-local 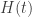 noise models the FTQC theorems that John Preskill has reviewed are rigorously true, in which case (it seems to me) Aram’s arguments formally prevail.
noise models the FTQC theorems that John Preskill has reviewed are rigorously true, in which case (it seems to me) Aram’s arguments formally prevail.
Conversely, -local
-local  noise models are associated to secular drifts in the Hilbert space, in which case (it seems to me) Kalai Conjectures 3 and 4 are rigorously true, so that Gil’s arguments formally prevail.
noise models are associated to secular drifts in the Hilbert space, in which case (it seems to me) Kalai Conjectures 3 and 4 are rigorously true, so that Gil’s arguments formally prevail.
From an engineering point-of-view, noise models are more realistic than
noise models are more realistic than 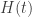 noise models — the latter models being the infinite-temperature limit of the former models — such that for practical purposes (it seems to me) Gil’s point-of-view presently prevails.
noise models — the latter models being the infinite-temperature limit of the former models — such that for practical purposes (it seems to me) Gil’s point-of-view presently prevails.
A logical next step is to see whether the FT theorems can be extended to encompass the secular drifts of finite-temperature Lindbladian noise … in which case the practical advantage in the debate will swing back to Aram’s point-of-view.
Overall, the Kalai/Harrow debate is becoming both increasingly-fun and increasingly-concrete in mathematical terms. And for this, my appreciation and thanks are extended to all participants! 😐 🙂 😀 😆
John, just because Gil uses a Lindblad evolution doesn’t mean that *all* Lindblad evolutions imply his conjectures. The one he proposes in his paper has flaws like ruling out classical fault tolerance, and having no known derivations from things we understand, like electromagnetism.
Also, I don’t think anyone is debating between Lindblad and Hamiltonian evolution. Obviously, *both* are valid ways of looking at the same system (up to the issue with being Markovian), depending on whether you trace out the environment or not.
Aram, my working appreciation of this question has always been that Lindbladian generators that are Hermitian (up to an irrelevant overall phase) can be unraveled as symplectomorphisms (that is, as random unitary transformations); otherwise not.
In physical terms, not every physically realistic noise process can be unraveled as a stochastic classical field that multiplies -local qubit operators. Rather, the noise processes that can be unraveled in this way are geometrically special (they are symplectomorphisms), and they are physically special (they can never relax qubits to a ground state, for example).
-local qubit operators. Rather, the noise processes that can be unraveled in this way are geometrically special (they are symplectomorphisms), and they are physically special (they can never relax qubits to a ground state, for example).
So perhaps these noise processes are computationally special too? In being special exceptions to Kalai’s Conjectures 3 and 4, which otherwise are generically true?
I will think about this more, over the weekend.
Joe, the principle that “not all physical interactions can be described by Hamiltonians” is actually quantum orthodoxy … it’s straight out of Nielsen and Chuang.
To see this, we need only take any POVM, unravel it as a continuous Lindblad process, and then express that Lindblad process as a (smooth) drift plus a (stochastic) diffusion.
Then a well-posed and mathematically natural question is this: Are the drifts associated with Lindblad processes Hamiltonian flows?
The answer (as one might expect) is “no”. Instead, Lindbladian drifts generically act to compress trajectories onto low-dimension submanifolds of Hilbert space (a compression that, by definition, no Hamiltonian process can accomplish).
Physically, this drift is the process that Woyciech Zurek calls einselection. Furthermore, we are free to regard any noise process as a covert measurement process, in which case “einselection” and “Lindbladian compression” are simply alternative names for a dynamical process that (in a coarse-grained projective limit) QM students are taught to call “wave function collapse.”
Summary: Non-Hamiltonian quantum dynamical flows are ubiquitous in Nature, and not everyone is certain that we understand their effects completely.
Sorry John, but I think something is getting lost in translation here. I am not suggesting that all open systems can be described be some Hamiltonian acting on the system alone. I’m not tracing out the environment. I’m saying that if you consider a given interaction you can write this as a Hamiltonian evolution on *some* system, although it may be bigger than the system you are considering for computation. You cannot simply write an arbitrary Lindbladian for a closed system.
Great comment!
Oh, I don’t think we’re disagreeing, Joe. My point was addressed to the moderately skeptical school of thought that is:
(1) collegially sympathetic to the Kalai conjectures, and yet is
(2) rigidly orthodox with respect to the doctrines of the “The Church of the Larger Hilbert Space” (as set forth in Nielsen and Chuang, for example).
To speak metaphorically, the non-Hamiltonian dynamical flows that are induced in large- qubit systems by quasi-continuum noise baths are sufficiently corrupting as to induce skepticism even in fervently devout churchgoers. It doesn’t really help much to say “Yes, but doctrine tells us that non-Hamiltonian flows on qubit state-spaces are Hamiltonian on some larger state-space.” Because as a practical matter, at some point in the analysis of FTQC, the expansion into ever-larger Edens of Hilbert Space must terminate, and at that termination-point, the Serpent of non-Hamiltonian noise enters into Eden.
qubit systems by quasi-continuum noise baths are sufficiently corrupting as to induce skepticism even in fervently devout churchgoers. It doesn’t really help much to say “Yes, but doctrine tells us that non-Hamiltonian flows on qubit state-spaces are Hamiltonian on some larger state-space.” Because as a practical matter, at some point in the analysis of FTQC, the expansion into ever-larger Edens of Hilbert Space must terminate, and at that termination-point, the Serpent of non-Hamiltonian noise enters into Eden.
Then the mathematical point is that the Serpent has two aspects: a diffusive aspect that is a zero-mean stochastic process, and a drift aspect that is a non-Hamiltonian flow-field on the qubit Hilbert space. In particular, the geometry of the Serpent’s non-Hamiltonian flow on large- qubit state-spaces, as induced by quasi-continuum thermal baths, is sufficiently cunning that we do not presently have an entire appreciation of it. That is why even devout Eden-believers — church-goers like Gil Kalai, Steven Weinberg, John Preskill, Aram Harrow, Scott Aaronson, and many more — appreciate that in Feynman’s phrase, “It has not yet become obvious that there’s no real problem.”
qubit state-spaces, as induced by quasi-continuum thermal baths, is sufficiently cunning that we do not presently have an entire appreciation of it. That is why even devout Eden-believers — church-goers like Gil Kalai, Steven Weinberg, John Preskill, Aram Harrow, Scott Aaronson, and many more — appreciate that in Feynman’s phrase, “It has not yet become obvious that there’s no real problem.”
Gil,
Regarding this statement
“The problem is with its consequences which are questionable. (I tend to think that the consequences are even unreasonable, but I firmly believe that these spectacular consequences should be questioned.)”
Maybe it would be good for the discussion if you stated which unreasonable consequences you mean? Are these the efficient algorithms for certain problems which would be possible on an quantum computer or do you mean something else?
Reply to John Preskill (cont.): Hamiltonian models:
Let me continue my remarks on points made by John Preskill
John’s Hamiltonian model
(John Preskill): “In my earlier comment I gave an example: a Hamiltonian noise model such that a threshold theorem can be proven if the operator norms of the terms in the Hamiltonian obey a suitable criterion. Conceptually, this model has the nice feature that we don’t need to assume anything about the initial state of the bath beyond the assumption that is it possible to cool individual qubits (prepare a qubit in a state close to the standard “spin-up” state). This model may not be realistic, but why is it unacceptable as a matter of principle?” (link to the remark)
I like this model, and if you insist on describing a universal machine it is reasonable. And then it is not that the model is not unacceptable in principle, but that the principle would be that the “amount of noise” in terms of these operator norms will scale up. But this does not explain what is going on and for explaining what is going on you need to model special-purpose machines for quantum evolutions as well. For this purpose, I suspect that John’s model is unacceptable and that it is too coarse to be realistic or useful.
My Hamiltonian model
(John) “It would be helpful if Robert or Gil could exhibit families of Hamiltonians which allow fault-tolerant classical computing but disallow fault-tolerant quantum computing. Such examples would help to clarify where the disagreement lies.”
Well, I did present a family of Hamiltonian evolutions which is a subclass of all quantum noisy evolutions on n-qubit computers which are offered to model “non FT- quantum-computers.” This class is based on certain conjugated “smoothing in time” of the standard model, which express mathematically the idea that the system does not apply FT. I call this subclass of evolutions “Smoothed Lindblad Evolutions”. I think that it is a realistic mathematical task to show that they support my conjectures, and I suggest to start with Conjecture 1, but this was not done.
You can read about “Smoothed Lindblad Evolutions” either on pages 11-12 in my paper, “How quantum computers fail: Quantum codes, correlations in physical systems, and noise accumulation, or (with few more details and additional remarks) on pages 2-3 in my paper is “When noise accumulates. You can look also at pages 16 – 17 in the slides from the lecture at Caltech.
Thanks for these comments, Gil!
I may be missing something, but I don’t consider smoothed Lindblad evolution to be a Hamiltonian noise model. It is a non-Markovian evolution equation such that the correlations in the noise acting at a given time depend on the past evolution of the system. I’m interested in whether this model can be realized (perhaps approximately) by a Hamiltonian governing the joint evolution of the system and its environment, and if so what that Hamiltonian looks like. The environment would then serve as a memory which records information about the evolution prior to time t, and uses that information to “attack” the system at time t.
The Hamiltonian model I described in my write-up is likewise non-Markovian; it includes effects arising from the memory of the bath, and even allows the dynamics of the bath to be highly non-local. But fault-tolerant quantum computing can succeed against that model, because the processes in which the bath acts collectively on many system qubits are very rare.
I would like to see some examples of Hamiltonian models that describe the type of adversarial noise you envision; then we could try to assess whether these examples can be reconciled with other things we know (or think we know) about physics, from both theory and experiment.
“I may be missing something, but I don’t consider smoothed Lindblad evolution to be a Hamiltonian noise model. It is a non-Markovian evolution equation such that the correlations in the noise acting at a given time depend on the past evolution of the system.”
Actually, John, it is even worse. If you look at the formula you realize that the correlations in the noise acting at a given time depends on the entire evolution.
I don’t completely understand what you mean by “Hamiltonian noise model,” so perhaps this is the first thing to clarify. (I suppose this is also related to Joe’s comment above.) Isn’t “Hamiltonian noise model” simply means a quantum evolution described by a Schrödinger equation involving the qubits and the environment?
“Isn’t “Hamiltonian noise model” simply means a quantum evolution described by a Schrödinger equation involving the qubits and the environment?”
I believe that in the case where there is a two way interaction between the environment and the qubits a physicist would demand that the time evolution of the environment must also be given by a Hamiltonian.
This in contrast to the case where the environment affect the qubits, say through an infinite thermal bath, but the qubits do no affect the environment.
To make (what I take to be) your point another way, Klaus: we would like our noise models to be:
(1) Hamiltonian, and
(2) solvable, and
(3) realistic.
In practice, we can have any two of these attributes, but not all three.
Gil, it might help if we described the sort of “Hamiltonian model” we would find convincing.
In an ion trap QC where the qubit is stored in the electronic state of an atom, then spontaneous decay from the |1> state to the |0> state can be explained by spontaneous emission, which can be explained by coupling between the electron and the electromagnetic field.
A more complicated kind of noise comes from the control wires near the qubit. This too can be understood in terms of elementary physics: in this case, there are thermal fluctuations in the wire which are described by a mixture of Johnson noise and 1/f noise: the former from ordinary thermal equilibrium, and the latter by thermally activated longer-lived processes in the wire. Not everything is nailed down, but these are well-studied areas where people can do a good job matching experiment and theory. Here’s a recent paper talking about this:
http://arxiv.org/abs/1109.2995
So, we might find it more convincing if you had some kind of specific argument like “What you know about noise from control wires is still theoretically consistent with a plausible form of ‘detrimental noise’.”
Aram, I’ll offer an answer: “To a reasonable approximation, noise in the “control-wire class” is generically Markovian and finite-temperature.”
Specifically, with reference to John Preskill’s note of February 2, 2012, titled Sufficient condition on noise correlations for scalable quantum computing
, the assumed time evolution operator of Eq. 14,
is insufficiently general to leading order in the time increment : additional (non-unitary) evolution operator terms of
: additional (non-unitary) evolution operator terms of  should be retained (as usual in the analysis of Markovian noise processes).
should be retained (as usual in the analysis of Markovian noise processes).
It’s not clear (to me) whether the FTQC theorems still go through when these terms are retained, but the physical arguments that they should be retained seem pretty strong.
There’s what’s true, and there’s what we can prove.
I believe that proofs should go through if the k’th term in perturbation theory is upper-bounded by something like e^{-const * k}, which sounds consistent with what you’re talking about.
I believe that in fact FTQC works somewhat better than these over-pessimistic proofs would imply. Simulations have suggested this as well.
This isn’t to call for excessive optimism, but to realize that the rigorous proofs of FTQC are just one part of the story.
LOL … there’s a Richard Feymann quote for pretty much every idea in physics (including contradictory pairs of ideas). In the present case we have:
Thus, physicists “know” that perturbation theory fails when qubits interact with the spectrally white noise that is associated to a (quasi-)continuum of bath states (for example, the total spectral power associated to white noise diverges).
But fortunately, physicists “known” too that Itō-Stratonovich formalisms yield a physically valid differential description of the noisy dynamical trajectories … provided that the non-unitary operator terms are retained.
operator terms are retained.
Thus, it seems (to me) entirely reasonable to inquire whether the FTQC theorems survive when these physically well-justified quantum drift terms — which plausibly provide a concrete physical mechanism for Kalai Conjectures 3 and 4 — are included in the analysis.
Hi John, hi all
John Preskill wrote: “I would like to see some examples of Hamiltonian models that describe the type of adversarial noise you envision; then we could try to assess whether these examples can be reconciled with other things we know (or think we know) about physics, from both theory and experiment.”
Among my conjectures the one which I think is easiest to test against theory and experiment is Conjecture 1 about the realistic mixed states describing quantum codes. (In general, things are much clearer for codes.) The cases most interesting to me were specified as open problems in the first post and in some discussion in Aram’s first post. Namely, how mixed states representing anyons created experimentally look like, and what theory tells you in this case. And also the case of cluster states.
The rationale behind Conjecture 1 is the simplest to explain. When you encode r qubits with n qubits
with n qubits  errors in your input will be reflected as mixture of undesired codewords (unless FTQC is in place). This should agree with what we know from experiments because we do not have experimental evidence for quantum fault tolerance (yet). If predictions from Conjecture 1 does not agree with theoretic predictions, e.g., regarding anyons then we should doublecheck the theory, and this is very interesting. I don’t think we should wait for Hamiltonian models before testing Conjecture 1. I am also quite interested in the question
errors in your input will be reflected as mixture of undesired codewords (unless FTQC is in place). This should agree with what we know from experiments because we do not have experimental evidence for quantum fault tolerance (yet). If predictions from Conjecture 1 does not agree with theoretic predictions, e.g., regarding anyons then we should doublecheck the theory, and this is very interesting. I don’t think we should wait for Hamiltonian models before testing Conjecture 1. I am also quite interested in the question
Do you know?
Do you want to modify this a bit? In FTQC, you never perform an encoding map from r qubits to n qubits, except maybe when r=1. In general, you create a bunch of encoded |0> states, and then you build up your desired state by performing encoded gates on them. So there is no “input” that can have errors on it, other than the gate sequence.
Aram, yes, but when we think about realizing cluster states, or realizing Kitaev’s toric codes and their 4D analogs, or anyons, or various fragments of Shor’s algorithm, then conjecture 1, as stated, gives a clear prediction which is contrary to what standard noise models give. (But sure, we can consider modifications as well.)
To synthesize and summarize several previous comments, three documents that together compose a theorem-proving roadmap for allying the skepticism associated to Kalai Conjectures 3 and 4 are:
• John Preskill’s GLL note of February 2, 2012, titled Sufficient condition on noise correlations for scalable quantum computing,
• Ruediger Schack and Todd Brun’s A C++ library using quantum trajectories to solve quantum master equations (arXiv:quant-ph/9608004), and
• Carlton Caves’ internal report Completely positive maps, positive maps, and the Lindblad form.
Then in brief, a concrete theorem-proving roadmap is:
Step 1 Begin with John Preskill’s noise evolution operator [Preskill, eq. 14]:
Step 2 Augment the noise increment term with the drift and diffusion terms from Schack and Brun’s eq. 4 (here converted to Preskill’s notation)
noise increment term with the drift and diffusion terms from Schack and Brun’s eq. 4 (here converted to Preskill’s notation)
where are zero-mean Wiener increments, and concrete expressions for the Lindbladian increments
are zero-mean Wiener increments, and concrete expressions for the Lindbladian increments 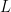 and
and  are given in Schack and Brun’s article.
are given in Schack and Brun’s article.
Step 3 Guided by Caves’ discussion of “the freedom to do arbitrary unitary remixing”[Caves, eq. 22ff], exploit that gauge-like freedom to choose Schack-Brun Lindbladian operators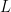 and
and  such that Preskill’s theorems can be extended to encompass (non-Hamiltonian) drifts and diffusions.
such that Preskill’s theorems can be extended to encompass (non-Hamiltonian) drifts and diffusions.
An accessible introduction to this general class of methods is Ian Percival’s textbook Quantum State Diffusion, in which we read [p. 47]
A key point is that in modeling finite-temperature and zero-temperature reservoirs it is not possible to choose Hermitian Lindbladian operators. And so (as it seems to me) proving Preskill-type FTQC theorems for this standard class of noise models might be quite challenging.
———
Summary To the extent that the above theorem-proving program can be extended to completion, then (as it seems to me) Aram Harrow’s nonskeptical side of the GLL debate will be greatly strengthened.
Conversely, to the extent that serious obstructions to strengthening the FTQC threshold theorems are encountered, then (as it seems to me) Gil Kalai’s skeptical Conjectures 3 and 4 can reasonably be regarded as being plausibly correct.
And finally, so long as these FTQC questions remain unaddressed, then (as it seems to me) this GLL debate can reach no compelling resolution.
———
Poscript Why aren’t I myself working to apply these methods to stronger FTQC theorems? It’s simple: these same methods are broadly applicable to challenges in quantum systems engineering that medical researchers like me regard as comparably interesting, fundamental, beautiful, and important to building quantum computers — and these medical challenges are my main research focus. And so it’s the math methods associated to the Kalai-Harrow debate that are of primary interest (to me); the outcome of the debate is naturally interesting, yet largely irrelevant to medical practice.
Some responses to some recent comments:
1) Aram about Smoothed Lindblad evolutions: “The one he [Gil] proposes in his paper has flaws like ruling out classical fault tolerance, and having no known derivations from things we understand, like electromagnetism.”
Aram, I will be very interested to understand what do you refer to especially regarding electromagnetism.
2) Aram: “So, we might find it more convincing if you had some kind of specific argument like “What you know about noise from control wires is still theoretically consistent with a plausible form of ‘detrimental noise.”
Sure, this is a natural challenge to consider. I think it is useful to propose bold mathematical models for “non FT quantum-computers” which will not depend on a specific architecture for the QC, and also to try to propose for specific architectures like ion traps computers what specifically can go wrong.
3) Aram: “I believe that in fact FTQC works somewhat better than these over-pessimistic proofs would imply. Simulations have suggested this as well.”
I completely agree with this.
4) Joe: “Can I further ask whether or not you think it is reasonable to restrict attention to 2-local Hamiltonians? The reason I ask is that this has a significant affect on how correlations can arise, since environmental systems must couple separately to different local systems within the computer. This certainly simplifies the fault-tolerance problem, but has strong physical motivation.”
Joe, I think that the answer is yes. (Certainly, if you can say interesting things related to our discussion with this 2-local-Hamiltonian assumption I will be interested to hear it.)
5) Thanks to Peter Shor who proposed to look at Computation by teleportation and Kitaev’s magic states.
6) John: “Yet [the debate is] largely irrelevant to medical practice.
Actually I’d personally love to hear about the medical practices you refer to (in a simple way that I can understand.)
Hi Gil,
Well, I believe if you accept 2-localness, or any other k-localness, of physical Hamiltonians you get exponential suppression of large correlations. To see this, consider the system Hamiltonian as . We take
. We take  , where
, where 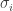 are Pauli operators, and that there is some small constant
are Pauli operators, and that there is some small constant  . In this case the system evolves as
. In this case the system evolves as  . Now, lets assume we only care about terms which produce a correlated error across
. Now, lets assume we only care about terms which produce a correlated error across  systems. Well, the only terms which can produce this must be at least
systems. Well, the only terms which can produce this must be at least  local, and since each term in
local, and since each term in  is 2-local (or k-local if you prefer), only the only terms which contribute are where
is 2-local (or k-local if you prefer), only the only terms which contribute are where  (or
(or  in general). Now, this already tells us that the characteristic time to produce
in general). Now, this already tells us that the characteristic time to produce  -local errors scales linearly in
-local errors scales linearly in  , which would already seem to spell trouble for your conjectures.
, which would already seem to spell trouble for your conjectures.
However, we can go further, by Trotterizing the time evolution: . Now, if we are performing the computation fault-tolerantly, evolution under
. Now, if we are performing the computation fault-tolerantly, evolution under  will preserve the weight of an error (i.e. the number of locations upon which it acts). Thus, only error terms must come from the
will preserve the weight of an error (i.e. the number of locations upon which it acts). Thus, only error terms must come from the  terms. But since we are taking the limit as w goes to infinity, the probability of a single $\latex \exp(i H_{noise} t/w) producing an error is less than approximately
terms. But since we are taking the limit as w goes to infinity, the probability of a single $\latex \exp(i H_{noise} t/w) producing an error is less than approximately  . Here the constant
. Here the constant  is present since there are less than
is present since there are less than  unique 1- and 2-local Pauli operators on $N$ qubits. For qudits you need only adjust the 16. Note here that N is the number of qubits in a single encoded logical qubit, not the entire computation. Hence the total probability of at least an m-local error scales as
unique 1- and 2-local Pauli operators on $N$ qubits. For qudits you need only adjust the 16. Note here that N is the number of qubits in a single encoded logical qubit, not the entire computation. Hence the total probability of at least an m-local error scales as  (or
(or  ). Thus for a fixed period of time
). Thus for a fixed period of time  corresponding to, say, a fault-tolerant gate and a round of error correction, the probability of an m-local error occurring scales as
corresponding to, say, a fault-tolerant gate and a round of error correction, the probability of an m-local error occurring scales as  , and hence for sufficiently weak noise (low J) the errors are exponentially surpressed, and mass correlated errors are impossible.
, and hence for sufficiently weak noise (low J) the errors are exponentially surpressed, and mass correlated errors are impossible.
But soberingly, under the Lindbladian substitution
this statement is less obviously true. E.g., under
(as in eq. 4 of arXiv:quant-ph/9608004v1), aren’t -local correlations effectively present in every order of a Lindbladian unraveling, even when the Lindbladian generator
-local correlations effectively present in every order of a Lindbladian unraveling, even when the Lindbladian generator  is
is  -local for
-local for 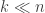 ?
?
We all appreciate that no amount of mathematical rigor can secure predictive capability to a theorem whose starting postulates are physically unrealistic. So one question that deserves to be discussed (in greater depth than has occurred so far in the GLL debate), is “To what degree is it physically realistic to assume that FTQC dynamical trajectories are perturbatively convergent?”
Or to put a sharper point on it: “Supposing that we unravel by standard (non-perturbative) Lindbladian simulation methods an -qubit quantum computation trajectory that perturbatively is rigorously fault-tolerant, will we generically find that the FT theorems fail for
-qubit quantum computation trajectory that perturbatively is rigorously fault-tolerant, will we generically find that the FT theorems fail for  ?
?
Although folks no doubt have passionate opinions regarding this question, to the best of my knowledge, no mathematically rigorous (or even plausible) analysis has appeared in the FTQC literature.
It would be great if some GLL reader could point to such an analysis, or alternatively (but less plausibly IMHO) provide some argument to the effect that Lindbladian noise models are not realistic in the context of FTQC.
Until such time, the case for moderate skepticism of FTQC remains (as it seems to me) moderately reasonable.
That’s of course correct Joe, but this is not what I meant (or thought that you meant).We know that quantum computers can be described by sequence of local operations on gates of size one and two, and my answer referred to the fact that I expect that my noise models also have this property. (E.g. if you describe the noisy evolution as a pure evolution on a large QC of the qubits plus the envoronment.)
About the notion of 2-localness (and k-localness) that you refer to here (and related notions), the situation is as follows: (We briefly discussed it already and this is mentioned in Ken’s summary to Aram’s post 2, but I will be more detailed this time.) :
1) The assumption that physics interactions and states are 2-local (or k-local for some small k ) is reasonable. (Conjecture C is meant to express this idea mathematically.)
2) This assumption is violated for states created by noiseless quantum computers (and used in most QC algorithms as well as FTQC) and indeed it gives a reason to be skeptical about QC.
3) In my models when you require the computer to create a state which is not k-local the noise will not be k-local as well.
4) A posteriori my noise models may explain why is it that we witness only states which are k-local for a small value of k.
Hi Gil and John,
I think perhaps both of you are miss understanding what I meant to convey, which is probably the result of me writing the comment in the middle of the night. What I meant was that we can construct the Hamiltonian such that
such that  contains only the (possibly time-dependent, usually piecewise constant) Hamiltonian of our desired computation, while
contains only the (possibly time-dependent, usually piecewise constant) Hamiltonian of our desired computation, while  contains the couplings to the bath. I guess I should also have added a
contains the couplings to the bath. I guess I should also have added a  which couples systems within the environment, but I just rolled it into
which couples systems within the environment, but I just rolled it into  as it does not affect the computation, and never increases the weight of an error.
as it does not affect the computation, and never increases the weight of an error.
The point was that we can describe essentially any physical system this way, independent of the computation we intend to perform, and indeed independent of whether we intend to use it for computation at all. Hence John’s Lindbladian objection and Gil’s points (2) and (3) don’t apply. So far this is just a general statement about systems and their environments assuming all Hamiltonians are 2-local or k-local. My constant isn’t quite correct (I left out a division by (m/2)! as well as well as some subtleties about amplitudes versus probabilities), but that isn’t really hugely important as far as I can tell. I should have also defined to be an upper bound on the total coupling of one computational system to the environment, rather than each system in the environment individually, which may have confused you (sorry, it was late).
to be an upper bound on the total coupling of one computational system to the environment, rather than each system in the environment individually, which may have confused you (sorry, it was late).
Still, it seems that you can apply this reasoning to any system where all of the Hamiltonians involved (in the system and coupling to the environment) are k-local. This includes when performing fault-tolerant computation, so I do not see how any noise models which require highly correlated errors not be exponentially suppressed can survive in such a setting, if J is sufficiently small.
Sorry, that should have been “misunderstanding” not “miss understanding”! I guess I am still tired
Dear Joe,
“Can I further ask whether or not you think it is reasonable to restrict attention to 2-local Hamiltonians?”
Now that you explained what you mean, the answer is: No
Ah, I see. But in this case, your assumption runs counter to known physics. At a low enough level all physical Hamiltonians are local.
Joe,
I think Gil would not want to suggest changes to the Standard Model.
But there do exist regimes in which we observe strong coupling, so high orders of perturbation theory are relevant. I guess we need to argue that such situations are highly limited, and never occur in a situation where the single-qubit, or two-qubit, error rate is below the FTQC threshold.
Sorry for the double comment. By local I mean k-local for fixed k, rather than 1-local.
Hi Aram,
Indeed that is true, but Gil’s argument seems to be that there does not exist a threshold, due to the existence of correlations in error. This should be true even at the ridiculously low levels noise where we can always restrict all Hamiltonians to be 2-local. Sure, this is way below the usual threshold, but it seems reasonable to consider this extreme. Further, there are many physical systems for which only 2-local Hamiltonians are relevant.
Sorry for yet another comment.
Aram: I should probably also have said that noise due to the strong and weak interactions necessarily falls off exponentially, simply because the density of qubits is presumably constant, and these interactions fall off exponentially spatially due to the massive gauge particles involved. Hence we need only really care about EM interactions (and I suppose gravity, but it is so weak we can probably safely ignore it).
Dear Joe and Aram,
Joe wrote: “Gil’s argument seems to be that there does not exist a threshold, due to the existence of correlations in error. This should be true even at the ridiculously low levels [of] noise where we can always restrict all Hamiltonians to be 2-local.”
I do not see at all why “at ridiculously low levels of noise we can always restrict all Hamiltonians to be 2-local.” (This statement seems in contrast to my conjectures.) In addition, my argument is that correlations in errors will go hand in hand with the noise rate (in terms of qubit-errors) scaling up. See this remark and this response to Boaz Barak (the later may be of interest to Klas).
We did have a previous round of discussion on 2-locality, and Ken’s summary from Aram’s second post looks good to me:
More generally we can propose:
Ah, now I think we are getting somewhere. The 2-localness seems to be a key point of disagreement. I have no idea what you mean when you talk about 2-locality of states etc. (I assume you mean that there is bipartite entanglement or something). However, it is a fact that the evolution operator is the same for all states if we take the entire environment into account (i.e. any shadow qubits etc.), and hence the operator does not depend on the particular state being processed. You seem to be disputing this, but I cannot figure out why (other than to get the type of noise you need). Clearly it is always possible to do this, since we could write everything in terms of the standard model. Certainly we need to be careful to make sure we take the entire environment into account in formulating our model, but this can of course be done, in which case the subsequent evolution operator is fixed and independent of the initial state. If not, you are suggesting a non-linearity in quantum mechanics (which I think is not your intention).
Hi Joe, very good, thanks for the remark. I also at times don’t understand what precisely you refer to. (E.g. when you say “everything in the standard model” do you refer to standard models of noisy quantum computers or to THE standard model of HEP which I dont see at all how it is relevant here.)
I think we are in agreement that the sort of states and evolutions that a QC can produce are vastly more complicated than states and evolutions we encounter in “known physics”; and my thinking about it is that the 2-locality that you referred to as “known physics” is related to the type of evolutions we actually encounter and that we cannot take 2-locality for granted when we push the envelope towards more exotic evolutions.
“However, it is a fact that the evolution operator is the same for all states if we take the entire environment into account (i.e. any shadow qubits etc.), and hence the operator does not depend on the particular state being processed.”
Well, I feel uncomfortable with arguments referring to “the entire environment”. (Last time we tried we ended up with the entire universe, and even there the argument was unconvincing.) But I also dont understand what you mean by “the evolution operator is the same”.
You seem to disagree for several reasons with my conjecture that when we create a mix state X that well-approximate a pure state Y the quantum operation E that describes the gap has systematic relation with the intended pure state X, systematic relation of the kind proposed by Conjectures 1,3,4.
Would you agree, that these conjectures are practically reasonable for, say, quantum computers with 30 qubits? Does your objection, in principle, to my conjectures apply there as well?
Please do try to have a look at what I say about special-purpose machines for approximating quantum evolutions, and see if you disagree, in principle, that for such machines everything can depend on the intended evolution.
Hi Gil,
I mean the standard model of particle physics. The reason this is relevant is that it is very hard to argue about all possible devices without saying something about certain properties that all possible devices must have. Hence the standard model. All possible quantum computing devices must be built up out of particles from the standard model. You are postulating a certain kind of noise, and I want to show that if the coupling to the environment is sufficiently weak, then such noise is not consistent with what we know about the physics of any such device. Actually I was trying to use it to shortcut any debate about whether restriction to k-local Hamiltonians is reasonable physically. As you say, this seems in tension with your conjectures, but we cannot simply ignore the fact that all noise is ultimately governed by known particle physics.
You say “I think we are in agreement that the sort of states and evolutions that a QC can produce are vastly more complicated than states and evolutions we encounter in “known physics””.
I disagree with the statement about evolution. The Hamiltonian evolution in a quantum computer is actually significantly less complicated than many structures which have been well studied. Polymers, magnets, etc. are a good example of this. The Hamiltonians we concern our selves with for building quantum computers are often already heavily studied in condensed matter, quantum chemistry, quantum optics etc. Certainly, you surely agree, we fully understand the evolution in linear quantum optics. Quantum electrodynamics is after all the most accurately verified model in physics.
As regards states, I agree that quantum computers will generate different classes of entanglement than have before been seen in a lab, but I am firmly wedded to linearity, and hence if I understand the evolution, I know how any state will behave. If that’s not true, then quantum mechanics is not a correct description of the universe, and all bets are off.
I do agree agree that the operation performed can have a relation to the state it produces (though as I have said before, this is not always the case, as in blind quantum computing). I do realise you are trying to use this to show that correlated noise can arise. The point of my last couple of posts, however, is that even when the evolution is determined by the target state, if the errors in the Hamiltonian are sufficiently weak (weak coupling to the environment and a good approximation to the ideal Hamiltonian) then we must still get exponential suppression of correlated errors (due to the fact that the Hamiltonians involved are k-local).
Do I believe your conjectures are reasonable for all 30-qubit systems we could build? No. Aram’s thought experiment is an example of a system where this is not reasonable.
I have been reading all your comments, it is simply that your conjectures (including your talk about special purpose devices) is simply incompatible with what we know about physics.
You seem to now be doubting that all relevant interactions are 2-local for pretty much all systems we consider because it is in tension with your conjectures. However, we know this to be true: the Ising interaction is 2-local, the exchange interaction is 2-local, dipole couplings are 2-local, photon emission and absorbtion are 2-local, Coulomb repulsion is 2-local. The list goes on and on. Even literally tripping over the power cord is a series of (strong) 2-local interactions.
well
Joe, again I am in trouble understanding what you mean precisely by 2-local.
We discussed error models where the probability of every qubit to be measured in a computer cycle is 0.0001 and the correlation between the events regarding 2 qubits is 0.05. Is this description 2-local?
Joe, I would agree with this assertion whole-heartedly, were it not that the state-space of every FTQC (known to me) contains either a divergent-dimension element called the “physical vacuum,” or else three quasi-continuum quantum descendants of the physical vacuum:
• photon/phonon sensors,
• photon/phonon sources,
• thermal baths.
Very broadly speaking, in FTQC these four elements serve as (necessary) entropy-sinks — a functionality that (by definition) no strictly Hamiltonian dynamical element can provide.
We all appreciate that the question “How do quantum vacua work?” is one regarding which many folks hold passionate opinions. It’s fun to discuss these opinions, and its especially fun to study the vast and still-growing literature relating to it, with the understanding that our present understanding of the quantum dynamical trajectories associated to quasi-continuous vacua is sufficiently incomplete that it is neither necessary, nor feasible, nor even desirable, that everyone think alike.
In which event, a diversity of physical intuitions, accompanied by vigorous debate, and clever experiments, that help to stimulate steady advances in mathematics, is just plain healthy for the whole STEM enterprise! 🙂 😀 😆
Conversely — and in consequence of this same diversity of opinion — it is just plain incorrect to assert as a meta-fact “We presently possess a reliable physical understanding of the dynamics of quantum vacua.” And that is the common-sense reason why (as it seems to me) moderate skepticism of FTQC is both moderately reasonable and good for the STEM enterprise as a whole.
Hi Gil,
No, this is not at all what I mean, and I guess this is behind the confusion. By 2-local, I mean that each term in the Hamiltonian acts on at most 2 subsystems (be they photons, electron spins, nuclear spins, etc).
John, the statement you are referring to is true in general. It is simply a statement of fact that the Lindbladian is an approximation, and if you believe the Schroedinger equation, then there is an exact Hamiltonian formulation.
Nothing changes because we care about a quantum computer, or even a fault-tolerant one.
Joe,
Do you regard Conjecture 1 as conflicting with “2-locality”? We discussed specifically three cases:
The first was BE states which were discussed in Matt’s comment. I expected noisy BE states to be a mixture of a cloud of different BE states (in additon to some standard noise).
(Of course, if you know more about the reality of noisy BE states I’d love to know.)
The second is my conjecture that noisy anyons created experimentally and considered as codewords will consist of mixture of different codewords in addition to standard noise.
The third is a similar conjecture for noisy cluster states.
Do you believe in Conjecture 1 for these cases, do you regard it being in conflict with 2-locality?
Hi Gil,
That is a very vague phrasing in the sense that of course I accept that there is some probability of finding yourself in an unwanted codeword in any physical system. However, my point is that if the system experiences only sufficiently weak noise (assuming Hamiltonians which cause this noise are 2-local), and assuming we follow a suitable fault-tolerant construction, then the probability of finding yourself in an unwanted codeword is exponentially suppressed in the distance of the code.
… that in coarse-grained FTQC frameworks is effectively projective, and that in fine-grained FTQC frameworks is effectively Lindbladian, and that in purely Hamiltonian FTQC frameworks is nonperturbative & divergent.
That all three frameworks have in the past yielded correct results (when applied with care by experts) no one doubts. That all three frameworks are subject to infelicities, absurdities, and even pathologies — even when applied with care by experts and particularly in the large -qubit limit — similarly no one doubts.
-qubit limit — similarly no one doubts.
That in consequence, none of these three FTQC frameworks — when applied in isolation and especially when not well-reconciled with the other two frameworks — reasonably suffices to allay moderate skepticism, is the point of a preceding remark.
It is in my view good news that these three FTQC frameworks are not fully reconciled: this means that plenty of good research opportunities are extant.
By definition, all moderate skeptics accept this. The point of debate is whether perturbative expansions in converge in the specific context associated to a given FTQC design.
converge in the specific context associated to a given FTQC design.
The school of “Hamiltonian moderates” argues “generically yes” and therefore rejects the Kalai Conjectures in consequence of the Fault Tolerance Theorems.
The school of “Lindbladian moderates” argues “generically no” and this establishes mathematical foundations for accepting the Kalai Conjectures.
It seems to me that most quantum systems engineers (quantum opticians in particular) are Lindbladian moderates, for the pragmatic reason that whenever qubits are coupled to a quasi-continuum of bath and/or sensor states, the dynamics of the qubits *is* Lindbladian.
Are there *any* FTQC designs in which the qubits are *never* coupled to a quasi-continuum of bath and/or sensor states? To my knowledge (and I am happy to be corrected) no such FTQC designs have ever been proposed.
Summary In the arguments presented so far, the Kalai side of the GLL FTQC debate has prevailed, in the sense that moderate skepticism of FTQC is mathematically rational under the physical assumption of finite-temperature Lindbladian noise.
Gee, now I wish the above post had described the starting postulates of the two contending schools-of-thought in the great GLL/FTQC debate as:
• Hamiltonian purism, versus
• Lindbladian realism,
in order to (eventually) argue the practical merits of an third alternative postulate that has considerable appeal to quantum systems engineers
• Kählerian radicalism,
regarding which there will (eventually) be a GLL post. 🙂 😀 😆
John, the Markovian approximation is simply wrong on short time scales. Ignoring this can lead to abominations unless you are very careful. If you ignore the actual dynamics of the bath in favour of a Lindbladian formulation you will convince yourself that refocusing is impossible.
Joe, we must all of us navigate very carefully between the Scylla of ultra-short time-scales and the Charybdis of ultra-high perturbative orders — because the history of physics shows us that abominable monsters lie in wait on both sides of this channel! 🙂 😀 😆
That is why prudent sailors chart their course by both Hamiltonian and Lindbladian doctrines … and when those two courses differ substantially — as seemingly they differ in the context of FTQC — then physical arguments verified by the best available experimental evidence, combined with deduction by the best available mathematical tools, historically have determined the best choice.
Thus, neither Hamiltonian purism nor Lindbladian realism reliably serves us when we regard them as “choose one” mathematical doctrines.
And even then, plenty of scientific sailors have ended-up shipwrecked, eh? Or else, navigating aimlessly upon uncharted seas of physics.
The net result is that the GLL/FTQC debate so far has been pretty evenly balanced between the minimal skepticism that is associated to Hamiltonian purism, versus the moderate skepticism that is associated to Lindbladian realism.
Summary The GLL/FTQC debate has not (yet) established solid reasons to be mathematically or physically confident in any of the charted courses for FTQC.
John, if you are suggesting that the Lindbladian somehow trumps the Hamiltonian description in some circumstances (other than in terms of mathematical convenience), then I cannot agree with you, and see little point discussing it further. The Lindbladian has a Markovian approximation built into it. When predictions from the Lindblad equation diverge from ones calculated explicitly (and hopefully correctly) from the Hamiltonian of the system, it is because the Markovian approximation has broken things. They are not both equally valid pictures of reality. One is exact, and one is an approximation, and it is the Lindblad equation that is the approximation. They are not on equal footing.
Respond to John Preskill (cont.)
Hi John and hi all, about Hamiltonian and other models:
Modeling Special-purpose machines for quantum evolutions, and smoothed Lindblad evolutions
Regarding the smoothed Lindblad evolution, my setting is this. Let us start with the following scenario. Suppose that a physicist wants to create a specific pure quantum evolution on n qubits. He sends the description of his evolution to the experimentalist or engineer and gets back a machine which approximate the required evolution. Let me call this setting the special-purpose machine scenario.
My proposal is that the evolution that the machine actually gives is described (approximately) by smoothed Lindblad evolution (plus perhaps some standard noise). This proposal refers to the type of approximations we can get experimentally to pure quantum evolutions. (It can also apply to the type of approximations we can expect in describing natural quantum evolutions, and to the type of noisy but approximately-pure quantum evolutions we encounter in nature.)
This smooth Lindblad evolution model is considerably wilder than the standard noise models. (Also , my model is non-geometric, so the initial noise operations, before the smoothing, can represent completely independent noise for different qubits. Of course, you can add geometric features if you wish but I see no reason to do it. The model has no “gates” and no specific “gate-errors”)
My proposal does not consist of throwing some “arbitrary Lindbladian” at the quantum evolution, but it is especially designed to describe mathematically “non fault-tolerance evolutions”. The idea is that if the evolution does not apply fault-tolerance to start with then this type of time-smoothing will not change much, so the smoothed noisy evolution will be a good approximation of the completely standard noisy evolution. However, this argument will break down for evolutions that exhibit the massive cancellation witnessed for quantum fault tolerance, and furthermore I expect that my smoothing will not allow quantum fault tolerance. (Of course, one can try to express mathematically “non FT-evolutions” in other ways.)
John wrote: “The environment would then serve as a memory which records information about the evolution prior to time t, and uses that information to “attack” the system at time t.”
This description is too simplistic for special-purpose machines. Remember that the machine we get from the experimentalist in our scenario depends on the entire evolution that you prescribed to the experimentalist. Such a dependence may be reflected by my “smoothing” (but again, other mathematical ways to reflect it can be suggested). In this setting the “environment” may “remember” everything, and this is reflected by the machine being part of the “environment”. I suspect that the above description adds to the notion “environment” some extra intuition that goes on top of the mathematics. This intuition may be justified for a truly general-purpose machine but is incorrect for the special-purpose machine scenario.
Modeling general-purpose quantum computers
Now suppose that after some time our physicist has a different, more ambitious, request from the experimentalist. He asks him to build a general-purpose controlled machine for quantum evolutions that will enable the machine to create every quantum evolution. Having a genuinely general-purpose machine for all quantum evolutions means that the modeling, including the description of the noise, is becoming simpler. How nice!
One can ask why to care about special-purpose machines if we really want to build general-purpose machines. And the obvious answer is that understanding the behavior of special-purpose machines will determine the feasibility of general-purpose machines. If it is indeed correct that the Hamiltonian noise model for special-purpose machines which approximate pure evolutions are always “non FT” (and this can reflect the dependence of the noise on the entire evolution, e.g. using my smoothed Lindblad evolutions), this will imply that for general-purpose machines with noise models like John’s recent one, the noise rate will scale up and FT will not be possible.
The smoothed Lindbladian evolution seems to say, if I am reading it right, that the noise at time t will be equivalent to noise applied at some early time t – Delta, and then acted upon by all the quantum gates that have happened between times t-Delta and t. Is that right?
In that case, if Delta >> t_gate (where t_gate is the time required for one quantum gate), then the noise will be highly nonlocal. Let’s say ~10 gates have happened in the meantime. Then on a 2-d grid, the noise could simultaneously strike ~100 qubits. This sort of thing seems pretty physically unprecedented. In the limit, you could say that noise always looks like it happened at the very start of the circuit. Of course then no error correction, classical or quantum, could ever work.
On the other hand, if Delta << t_gate, then this sort of noise is probably not a problem for FTQC to handle.
Delta should also be limited by measurement speed. Surely these memory effects cannot reach into the classical computer controlling the quantum computer, and for almost every proposed form of FTQC, there would be such a computer. This goes back to what Peter and Joe have been saying about teleportation/blind QC/etc, and also what I was saying about how every FT quantum computer is almost WLOG general-purpose. While a large entangled state is indeed being built up, that doesn't mean that we are acting on the same qubits a large number of times. We might be constantly introducing fresh qubits and measuring old qubits. It is entirely possible for each qubit to only be touched a constant number of times before it is discarded. At a certain point, the shadow qubits have to become mind readers!
“The smoothed Lindbladian evolution seems to say, if I am reading it right, that the noise at time t will be equivalent to noise applied at some early time t – Delta, and then acted upon by all the quantum gates that have happened between times t-Delta and t. Is that right?”
Very roughly. But we average over various Delta’s according to some kernel, and Delta varies on both positive and negative real numbers!
Delta is of the same time scale of the entire evolution. The model does not refer to any gates. But if you assume that the evolution represent M computer cycles then you can think about a typical Delta to be proportional to M.
Sorry for a delayed reaction, but better later than
never – here were few comments about repetition codes.
There are some differences in opinions and it hardly to
realize from them, but from the mentioned first post
(about flying…) it looks like it could be really useful.
I remember, how few years ago I have asked someone
(maybe, it was Alexei Kitaev), why three bits enough in
classical case, but for quantum case the analogue is a
9-qubits Shor’s code. Due to lack of answer I myself
made some investigation and, despite the reason could
not be explained in few words, it is really possible to
use “non-conventional” model of qubit that could allow
3-qubits error correction codes.
I would like to remind (also to myself) what is my main point in this discussion. The point is not at all to offer a “proof” that QC is impossible. The main point is also not to offer an argument for why QC are unlikely. It is true that I present several conjectures that, if correct, go against the possibility of QC based on quantum error-correction, and it is even true that I tend to believe that thee conjectures are correct but I am the first to admit that they have serious weaknesses and are at the very least counterintuitive. In my eyes the main point of these conjectures is to describe what Aram referred to as “non fault tolerance quantum computers” and in Daniel Gottesman’s beautiful picture above they describe the “desert of decoherence”. And describing non fault tolerance quantum computers is, in my opinion, an interesting project independently of QC skepticism.
The picture by Daniel Gottesman (that I include with Daniel’s permission) shows in a beautiful and funny way the world of quantum computation. (It goes without saying that Daniel disagrees with my position on FTQC.) Fault tolerant quantum computers which describe protected quantum evolutions are portrayed as “lands” surrounded by walls inside the desert of decoherence which allows only quantum evolutions not protected with quantum fault tolerance and quantum error correction. The United Classical Empire emerges in this desert of decoherence. My conjectures 1-4 and the smoothed Lindblad evolutions attempt to describe this desert.
As much as I practiced on my own blog I could not include the picture in the remark.
Alexander: the smallest quantum error-correcting code that can perfectly correct any single-qubit error has five qubits. For weaker types of errors, such as erasure or amplitude damping, 4 qubits will suffice. I believe that 3-qubit codes only protect against errors that are essentially equivalent to classical errors (i.e. bit flips only, or phase errors only).
Aaram: I mean a non-standard model of qubit.
Joe’s 2-locality argument
Joe have made an appealing and interesting argument against my conjectures which goes as follows:
1) All physical processes known to us are 2-local, namely the Hamiltonians can be described by terms acting on at most pair of particles.
2) If we relax the condition of the threshold theorem and assume that the Hamiltonian describing the noise contains only terms corresponding to pairs of qubits the threshold theorem will still hold (with a smaller threshold).
3) Therefore conjectures 3 and 4 about correlated errors are in contrast with what we know from physics.
Quoting Joe: “You seem to now be doubting that all relevant interactions are 2-local for pretty much all systems we consider because it is in tension with your conjectures. However, we know this to be true: the Ising interaction is 2-local, the exchange interaction is 2-local, dipole couplings are 2-local, photon emission and absorbtion are 2-local, Coulomb repulsion is 2-local. The list goes on and on. Even literally tripping over the power cord is a series of (strong) 2-local interactions…”
Don’t give up two soon, Gil! For example, the Ising model’s Hamiltonian is 2-local; moreover for finite -particle systems its partition function is trivially analytic; thus for in every finite
-particle systems its partition function is trivially analytic; thus for in every finite  perturbative expansions are rigorously convergent … yet in the limit
perturbative expansions are rigorously convergent … yet in the limit  perturbative expansions of the Ising model’s partition function fail utterly. That is why (it seems to me) a key, unanswered, physically subtle, and mathematically difficult question in this GLL/FTQC debate is “Under what circumstances are perturbative descriptions of quantum noise and measurement processes trustworthy?”
perturbative expansions of the Ising model’s partition function fail utterly. That is why (it seems to me) a key, unanswered, physically subtle, and mathematically difficult question in this GLL/FTQC debate is “Under what circumstances are perturbative descriptions of quantum noise and measurement processes trustworthy?”
Dear John,
“Don’t give up too soon, Gil”
For me, giving up (on such matters) is always an option. Give me a good argument, or a good experimental evidence, and I will give up with no regrets.
Specifically, a very similar point to what Joe is making was briefly addressed already in the very last paragraph (p. 18) of my paper “when noise accumulates,” so I do not see a reason for giving up on this occasion and it will be very nice to discuss Joe’s point thoroughly. Joe did a great job yesterday in our discussions and I wanted to give him both a credit and a happy break of a day or so, and also give myself a short break to rethink this issue.
Thanks also for your technical remarks on perturbative descriptions of quantum noise.
I am still playing with this idea what I am calling a Naive Noisy Toy Model (NNTM) based on some of the ideas picked up in [1][2][3] which follow along with this discussion pretty well. What I am imagining (right or wrong) is that I have some density matrix $\rho$ representing the system I am interested in. As time progresses, noise is introduced by performing successive tensor product operations of the original density matrix and a noise matrix for each instance of noise 1 to N.
$\rho \otimes \chi{1} \otimes \chi{2} \cdots \chi{N}$
So each successive instance of noise has the effect of growing the hilbert space and the overall density matrix [1]. Each instance of noise effectively brings with it some random phase factor and basis, which is distributed about some mean value representing zero. The idea being that we have to introduce noise into the system in such a way that any measurement of the system will give the appearance of non-correlated results that becomes more difficult to understand after each noise event.
The thought is to model the environment not as some large system that is always there. Instead as time progress there is distinct intervals between noise events such that normal Hamiltonian evolution can occur between events but that there is a growth in the density matrix of the system at each noise event. We simply don’t have any idea of what the true basis is by which to perform measurements on the system.
[1]http://www-bcf.usc.edu/~tbrun/Course/lecture17.pdf (slide 16)
[2]http://books.google.com/books?id=tLJWWe4RiroC&pg=PA196&lpg=PA196&dq=pointer+states+quantum+mechanics&source=bl&ots=ezG3KvvX-0&sig=qoZ6B-BoZ3pgG9LDGIOsJnvA3ic&hl=en&sa=X&ei=RaZiT93wDcnb0QGMqojCCA&ved=0CGEQ6AEwCTgK#v=onepage&q=pointer%20states%20quantum%20mechanics&f=false
[3]http://www.ipod.org.uk/reality/reality_boccio2.pdf (page 3)
Hal, I think that is misguided. If you only take the tensor product and don’t actually interact the subsystems, then the subsystem containing the computation is noiseless, and you can simply make a measurement of (say) Z on a qubit in this subsystem tensored with the identity over the other subsystems and it will yield the same result as in the noiseless case. So even though it is potentially hard to find basis states diagonal in the noise, there is a simple measurement you can make. You suggestion is mathematically equivalent to looking first at (say) an electron, and then ever more systems surrounding the electron without ever having them interact. In any case, you get the same result by simply only measuring the electron.
Thanks,that is great input. One thought that is nagging me is some of the discussion in chapter 3. Specifically the point that inputs and outputs of QFT assume that systems evolve from non-interacting to non-interacting. We normally seperate the Hamiltonian into two seperate entities, the non-interacting and the interacting part. In most treatments of noise that is what is done and there is a considerable amount of study in the interacting part. In any case, what we develop is the scattering matrix S which is what evolves the system. So the question seems to be one of trying to build a general approach to building a scattering matrix.
http://books.google.com/books/about/Diagrammatica.html?id=Dzb92Y3GZ1oC
Sorry…chapter 3 of Diagrammatica
Aram, when you get to it, please explain your Smoothed Lindblad evolution and electromagnetism remark.
Sorry for not replying before.
I meant that smoothed Lindblad evolution involves highly entangling noise, and appears to corresponds to effective Hamiltonians with k-qubit terms for large k. (I think k would scale in your model like (memory time / gate time)^dimension.)
Whereas if you look at the type of interactions that actually are relevant for any proposed implementation of QC, then gravity and the weak and strong force are not important, and it’s all about electromagnetism. This is a known theory, and consists of a bunch of interactions that are essentially pairwise. For example, in the classical version (Maxwell’s equations), one electron creates electric (and sometimes magnetic) fields that exert forces on other electrons. The field strength is linear in the number of electrons (although it does go to infinity as distance to an electron goes to zero), and the force on an individual electron is linear in the field strength. Equivalently, the energy is a quadratic function of the occupation numbers of the different possible electron states, reflecting the fact that interactions are between pairs of electrons. (This is also true quantumly.) If there were a k-qubit interaction, this should be reflected in some energy scaling like the k’th power of the number of electrons.
And this is consistent with the kind of noise we observe experimentally.
For example, electrons (due to their charge and spin, mostly) are magnetic dipoles, and so interact with each other via a dipole-dipole coupling. If we store qubits in the spin of electrons (or nuclei), then they can couple to other dipoles and cause decoherence. But this sort of coupling generally always looks like a sum of a bunch of pairwise interactions.
The only tricky part is that there are sometimes *effective* higher-order interactions, e.g. in transistors. These can definitely be engineered, and often happen naturally. But typically (in weakly interacting systems), their strength decays exponentially with k. (More precisely, weakly interacting systems are ones where we can perform a convergent perturbation expansion around a non-interacting theory, whereas strongly interacting systems are ones where we don’t know how to do this. There is some imprecision in the labels because sometimes a change of basis can simplify a system and cause things to become weakly interacting or even non-interacting.)
Quantum computing implementations are pretty much always in weakly interacting systems (although there may be subtleties if strongly interacting systems exist nearby), which is why most physicists tend to believe the assumptions of FTQC. I guess John Sidles’s skepticism comes from the sense that many systems are strongly interacting. Maybe in another comment, I’ll talk about why I don’t think this should worry us.
Thanks, Aram.
————————-
Numerically verifying Kalai Conjectures 3 and 4:
Four particularized steps toward the Aaronson Prize
————————-
Aram, that is a fairer one-sentence summary than I could have written myself … thank you.
This too is (IMH0) a perspicacious remark; the independent oscillator (IO) noise model of the much-cited Ford Louis and O’Connell article “Quantum Langevin Equation” (1988) provides analytically tractable examples of this weak-strong interaction duality.
… which is a sufficiently small enough number that the Lindbladian evolution of one or two LMPZ-encoded qubits can be numerically unraveled on a laptop computer, and three LMPZ-encoded qubits can be numerically unraveled on a cluster.
Then by the following particularized computational path, it is feasible even for undergraduate students to numerically test Kalai Conjectures 3 and 4, and thus contend (seriously) for the Aaronson Prize.
——————–
Numerically verifying Kalai Conjectures 3 and 4:
Four particularized steps toward the Aaronson Prize
Step 1 Specify -local Lindbladian generators corresponding to Bloch parameters
-local Lindbladian generators corresponding to Bloch parameters  and
and  (inverse temperature) arbitrary, such the single-qubit density matrix relaxation is
(inverse temperature) arbitrary, such the single-qubit density matrix relaxation is  , for
, for  the usual
the usual  Pauli spin matrix.
Pauli spin matrix.
Step 2 For the special case of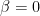 (infinite temperature) the unraveled Lindbladian evolution is Hamiltonian; hence the standard FT (fault tolerance) theorems formally apply. Run the LMPZ algorithm projectively at a fixed time interval
(infinite temperature) the unraveled Lindbladian evolution is Hamiltonian; hence the standard FT (fault tolerance) theorems formally apply. Run the LMPZ algorithm projectively at a fixed time interval  . Verify numerically that the expected error rates are achieved for
. Verify numerically that the expected error rates are achieved for  encoded qubits.
encoded qubits.
Step 3 For the physically realistic case of (that is, finite temperature noise) — and in particular for the case
(that is, finite temperature noise) — and in particular for the case  (that is, a physical temperature limit of
(that is, a physical temperature limit of  ) — the unraveled Lindbladian evolution is non-Hamiltonian; hence the standard FT (fault tolerance) theorems formally do not apply. Moreover, Kalai Conjectures 3 and 4 (in a strong reading of them) predict a finite-
) — the unraveled Lindbladian evolution is non-Hamiltonian; hence the standard FT (fault tolerance) theorems formally do not apply. Moreover, Kalai Conjectures 3 and 4 (in a strong reading of them) predict a finite- error rate that is a strongly convex function of
error rate that is a strongly convex function of  . The numerical task of Step 3 is to verify
. The numerical task of Step 3 is to verify  -convexity of the qubit error rate for
-convexity of the qubit error rate for  encoded qubits.
encoded qubits.
Step 4 (extra credit: Aaronson Prize contention) To answer objections of the class “Hamiltonian dynamics is exact, and Lindbladian dynamics is an approximation,” repeat Steps 1–3 numerically within the Ford-Lewis-O’Connell IO noise model (which is mathematically Hamiltonian but physically Lindbladian). Finally (and hardest) establish by rigorous analysis that the large- scaling of the
scaling of the  -convexity of finite-temperature IO-model qubit error rates is adverse for FTQC.
-convexity of finite-temperature IO-model qubit error rates is adverse for FTQC.
——————–
Any student (or team of students) embarking upon this stepwise path is advised to deconstruct, paragraph by paragraph, Scott Aaronson’s IEEE Spectrum essay “Why I’m Wagering $100,000 on Quantum Computing,” in particular Scott’s thoughtful remarks as follows:
Summary There exist specific mathematical and physical intuitions, and a particularized computational path, by which student-level computational experiments can help convert the vision of Scott’s $100,000 wager into the “absolutely thrilling” reality of feasible quantum systems engineering simulations, by numerically verifying Gil Kalai’s Conjectures 3 and 4 in realistic test-cases, via well-posed simulation algorithms that have immediate application to urgent practical problems in engineering and medicine.
John: It sounds like you are suggesting an experimental method to prove the conjectures, but the experiment should be performed by simulation on classical computer. Why? I supposed, that even currently computer simulations less powerful, than real experiments in a laboratory. If you need to simulate that on computer, may be it is some sign, that conditions necessary for proof of the conjectures are not realistic enough to be tested experimentally? I myself think that it is too early to embark in error correction codes, before learning something from experimental tests with few dozens qubits performing something nontrivial even with errors.
Alexander, nowadays it is typical for systems engineering groups to generate, each week, terabytes of unraveled dynamical trajectories. Analysis of these trajectories (which can be classical, quantum, or hybrid) helps enterprises design experiments, optimize prototypes — and conceive mathematical theorems too — at a far faster pace and with far greater assurance, than would otherwise be the case.
A Google search will find a brief on-line research note by Markus Deserno, titled “Microcanonical and canonical two-dimensional Ising model: an example” that illustrates the rich interplay of theory, simulation, and experiment … nowadays no one of these three methods is notably privileged over the other two.
Oh, and to be a little more clear, Deserno’s short essay regards the formal equivalences and the numerical differences respecting two methods for simulating ensembles of dynamical trajectories:
(1) the microcanonical ensemble (thermodynamicist language) of Hamiltonian trajectories (QIT language), versus
(2) the canonical ensemble (thermodynamicist language) of Lindbladian trajectories (QIT language).
Thermodynamicists often give the name thermostats to elements of their dynamical simulations that QIT researchers call Lindbladian … an Arxiv full-text search for ensemble and thermostat provides 1210 examples of thermostatic noise simulation.
It is reasonable to say that, on the one hand, thermostatic/Lindbladian simulation methods are theoretically well-understood, and experimentally well-verified, and exhibit significant practical advantages relative to microcanonical/Hamiltonian methods, yet on the other hand, their proper application (as with all noise analyses) does require careful case-by-case mathematical analysis combined with a well-developed physical intuition.
That is why, for thermodynamicists and condensed matter physicists especially, noise analysis is arguably the most mathematically challenging, physically interesting, and even practically important aspect of FTQC.
Obviously, even reading and integrating the various schools of literature is a pretty considerable challenge! 🙂
John, I’ll make a pitch for one of my own old papers here. I and my coauthors demonstrated how one use a bit of finite field theory to make this type of microcanonical computations for far larger systems than the side 32 lattice mentioned in the paper you linked to.
http://abel.math.umu.se/~klasm/Uppsatser/plancheb.pdf
Klas, your Ising model article is outstanding … even magisterial. I had wondered why Deserno never expanded his brief 2004 research note into a full article, and now I know one reason: the high-order (up to 320×320) expansions in your 2005 article largely supersede Deserno’s low-order (32×32) expansion.
Without any claim to have a full understanding of the detailed workings of your analysis, it appears (to me) that the heat-capacities of your Fig. 2 result from large-grid evaluations of the canonical-ensemble specific heat that Deserno gives (formally) in his Eq. 8. It is natural to wonder, whether it is computationally feasible, via inverse Laplace transforms, to analytically compute the microcanonical-ensemble specific heat (i.e., Desarno Eq. 7)? In other words, does your work provide the results needed to extend Figure 2 of Desarno’s note, to Ising-model grids of 320×320? If so, that would be a cool calculation. There’s always more interesting questions, in noise-modeling! 🙂
These considerations prompted me to review the discussion of noise in the initial 2002 draft of QIST: A Quantum Information Science and Technology Roadmap, Version 1.0 (LA-UR-02-6900, 2002). The review of QIST Version 1.0 was quick; the word “noise” appears nowhere; instead “decoherence” appears throughout; and there is no anticipation that fundamental obstructions associated to decoherence will be encountered.
However, in QIST Version 2.0 (LA-UR-04-1778, 2004) the following question is raised deep within the QIST Roadmap (specifically, as technical issue #6.7.5.2.1) :
In retrospect, this prescient 2004 QIST question provides a starting-point for both Gil Kalai’s Conjectures 1-4 and — of even broader and more urgent practical consequence — it is a precursor of the thrillingly fundamental question with which Scott Aaronson’s IEEE Spectrum essay now challenges us: “What is the fast classical algorithm for simulating quantum systems?”
John, we compute the exact coefficients of the partition function, so we get the exact microcanonical values, and the exact canonical ones for all temperatures.
But this is getting very much off topic.
Hardness of simulation of quantum systems was a starting point for Feynman to suggest idea of quantum computer. So examples with classical systems do not look quite appropriate. As for decoherence, it should be distinguished from noise, errors, etc. Sometimes a highly entangled state may be even more stable against decoherence than any non-entangled one, simply because it is the ground state of some physical system.
Klas, my point is that a presently contentious issue in the GLL/FTQC debate (namely, Hamiltonian versus Lindbladian unravelings of thermalized trajectories) is a formerly contentious issue in thermodynamics and statistical mechanics (namely, microcanonical versus canonical unravelings of thermalized trajectories) — and so is worthwhile to study how the condensed matter physics community resolved these issues … because the history of physics shows us that these issues are not simple or easy.
Alexander, that’s true, but on the other hand, this history of physics teaches us that Feynman’s intuition in these matters was fallible.
John, what is “intuition” you are talking about? Hardness of simulations of quantum systems is a clinical fact for people trying to develop such simulations. Feynman just suggested a fresh idea to manage with that.
It is the intuition that the QIST Roadmaps (for example) express as follows:
Where is second citation is coming from? Roadmap does not contain term “intuition” at all
It is probably time to carefully examine some aspects of Joe’s interesting locality argument. In a sense Joe’s argument is like “fighting censorship with censorship”, as it uses an interesting censorship hypothesis on the nature of natural (uncontrolled) quantum processes (2-locality) to “fight” conjectures which propose some limitations on the type of feasible states and evolutions of controlled quantum evolutions.
I have some preliminary questions mainly for Joe to get going.
1) (Joe) “Even literally tripping over the power cord is a series of (strong) 2-local interactions…” Joe, What precisely do you mean and how this is done? Do you allow models based on a series of 2-local interactions?
2) Do you regard the 2-locality restriction as a certain law of physics that hold “on the nose” or would you accept k-local for larger k’s with smaller weights?
3) Aharonov, Kitaev and Preskill, and more recently (over here!) Preskill considered noise models where correlations decay as a function of the distance and still allow the threshold theorem. Do you regard these models as 2-local (and if so would this give an immediate proof for the threshold theorem for them), would you regard such a decay as unrealistic if it is not based on 2-local Hamiltonians? (which is also very interesting.) Is your comment shed light on the status of the threshold theorem for decay behavior which is still left open in these works?
4) (Most important, in a sense). Why do you regard what you are proposing as being in contradiction with what I am saying? In particular I draw your attention to my last comment to John Preskill?
5) What is the fundamental reason, in your view to the 2-locality rule?
Hi Gil,
Well, if you treat nuclei as individual systems, you can write down the potential felt by the nuclei and electrons in a material pretty much exactly as a series of one- and two-body terms. This is just as true of air as it is of steel. When you yank out a power cord, the force is propogated through by two-body interactions. Think of a simple metal chain: each link is only coupled pair-wise to its neighbours, so it is no surprise that this can propagate information.
k-local should have the same consequences as long as k is fixed, but really everything that can be understood in terms of electromagnetic interactions necessarily can be written in terms of only 2-body interactions. This is not true of (for example) the strong interaction (here I mean the nuclear force, not merely strong couplings), but both the strong and weak interactions have massive gauge bosons which ultimately means they fall of exponentially in space (unlike EM and gravity, which fall off only polynomially).
I’m not sure exactly which work you are referring to. Correlations falling off with distance does not imply a 2-local Hamiltonian: there are 2-local Hamiltonians which have long range interactions (i.e. the mean field model) and there are k-local Hamiltonians which can have correlations which fall off with distance.
As I say, I don’t know exactly which papers you mean, and I guess I haven’t read them in any case (not a criticism, I just have finite time and this isn’t really what I work on), so am probably not in the best position to comment on what is or isn’t left open by them.
Well, as per my comment http://rjlipton.wordpress.com/2012/03/05/the-quantum-super-pac/#comment-19216 it would seem that if you require that the Hamiltonian coupling a system to the environment and any systematic error terms in the system Hamiltonian are restricted to being 2-body, for a fixed period of evolution if you make these couplings sufficiently weak, errors are surpressed exponentially in their weight. This seems to rule out the kind of correlations your noise requires.
Basically you can think of it like this: Imagine I have a row of beer bottles on the wall, each with a thread coming off it. If the thread is strong, I can get a correlated error by yanking all the threads simultaneously, but if the threads are very weak all I am doing is raising the independent error probabilities for each falling off.
EM is pretty weakly interacting and we can understand electromagnetism in terms of pairwise virtual photon exchange, but this is a sort of chicken and egg situation. I don’t claim to know why we have the fundamental interactions we do. No one really yet knows why we have the physics we do.
Thanks, Joe, that’s interesting!
“We know this to be true [all systems we consider are 2-local] : the Ising interaction is 2-local, the exchange interaction is 2-local, dipole couplings are 2-local, photon emission and absorbtion are 2-local, Coulomb repulsion is 2-local. The list goes on and on…”
If I understand you correctly your central claim is that all natural physical systems are 2-local.
Modelled via quantum computers, I suppose that 2-locality does not refer to every (polynomial time) evolution described by a noiseless quantum computer with gates acting on one or two qubits. (This leads to universal quantum computers and if we give the noise such a power we can kill the computation.)
Joe, how would you express 2-locality in terms of quantum computers? Would you give, a “2-local system” the power of a single cycle in a noiseless quantum computer? Or perhaps the power of a bounded number of cycles?
(Of course, the next question would be why do you think that 2-locality should be imposed on the model, rather than be a consequence of the model. But perhaps I should first understand what do you precisely mean by 2-local systems.)
Just to focus the question a little more: Is a quantum computer running Shor’s algorithm a 2-local system?
Not everything, but everything relevant (i.e. the strong interaction is not relevant etc.).
I’m talking about the generating Hamiltonians. The gate model you describe is indeed 2-local, but but your statement that we can kill the computation ignores what I said about the strength of the noise. As I say, the couplings must be below a certain (low) threshold, otherwise you do not necessarily get the exponential falloff.
I don’t know what you mean. You can form any computation from purely 2-local Hamiltonians.
Any physical one we build out of atoms and electrons interacting electromagnetically will ultimately come down to a series of 2-local Hamiltonians, but I can certainly give you a universal set of Hamiltonians which is not 2-local.
I’m sorry, I thought I had made it clear that I was talking about 2-body interactions when I talk about 2-local Hamiltonians.
Gil, with regard to the generating Hamiltonian(s) of the quibit gates, there is a reasonably uniform scientific consensus (as Joe Fizsimons’ post affirms, for example) that the answer is “yes”.
Yet with regard to the photon/phonon sources and detectors that are necessary to the “FT” elements of FTQCs, there is a reasonably uniform scientific consensus (as the formalism of arXiv:quant-ph/0506118v3 affirms, for example) that the answer to your question is “no.”
Whether the generic non- -locality of microscopic models of noise and measurement is incidental or fundamental to the feasibility of FTQC, is (to my knowledge) a topic that has never been surveyed in the QC literature.
-locality of microscopic models of noise and measurement is incidental or fundamental to the feasibility of FTQC, is (to my knowledge) a topic that has never been surveyed in the QC literature.
If such a survey article were to appear, plenty of folks from many STEM disciplines would read it with great interest … given this diverse readership, and given the immense amount of literature extant, it is implausible (in my opinion) that any such survey article would be short, or easily assimilated, or definitive in its conclusions.
If any GLL reader can provide candidate references (or alternatively, explain why there is no need for such a survey) that would be terrific! 🙂
Hi Joe, at the end it is indeed not clear to me what your precise claim and justification is. If you say that in a single computer cycle the noise is expressed by a quantum operation which can be written as the sum of terms representing actions on two qubits, such that the error rate is small, then indeed this model supports the threshold theorem. If you allow that the noise will represent a series of such 2-local operations (like what we witness in a quantum computer) then it is possible to create damaging noise operations, namely, models where the exponential decay will not be satisfied. So at the end your argument is similar to the claim that the standard noise models for quantum computers which support exponential decay above the error rate are reasonable. Yes, they are a priori quite reasonable!
The ingredient that seems interesting is the claim that your modeling is “forced” by the limitations we see for natural quantum processes. (Perhaps even by the standard model!)
The general structure of this claim is this: The more limited the types of quantum processes witnessed in nature are, the easier it becomes for us to create exotic quantum processes.
(Because we have to fight simpler kind of noise.) Of course, it also comes to reason that the correct logic is rather: The more restricted the types of quantum processes we witness in nature are, the less likely it is to expect that we can create the exotic quantum processes.
Remember from the comment that I referred you to that the picture I am trying to draw (which supports the second logic) is the following:
Universal architecture for quantum computers like universal James Bond cars can only serve as sculptures, they will not work. (In other words, the error rate will scale up.)
For special-purpose machines for creating quantum processes, if the machine achieves the goal and well approximate the intended evolution, there will be interesting relations between the noise and the entire intended evolution. (My Smoothed L. E. is a specific suggestion for that, as well as Conjectures 1-4.)
This will explain the limitation on natural quantum processes (of the kind you referred to) as well as similar limitation of quantum processes we can create.
Hi Gil,
My argument can be seen as being composed of several parts.
1) I am suggesting that the following is true: Given an ideal possibly time dependent Hamiltonian for the evolution of the quantum computer which conserves the weight of errors (i.e. a standard fault-tolerant construction), a Hamiltonian for the environment, and a noise Hamiltonian consisting of only 2-body terms , then for a fixed period of evolution $T$ there exists a critical coupling strength $J_\text{crit}$ such that if $J_\text{crit} > \sum_i J_{ij} \forall j$ then the probability of a weight
, then for a fixed period of evolution $T$ there exists a critical coupling strength $J_\text{crit}$ such that if $J_\text{crit} > \sum_i J_{ij} \forall j$ then the probability of a weight  error occuring is exponentially small in
error occuring is exponentially small in  .
.
Clearly this is a mathematical statement which can be proved true or false (as I tried to prove in the comments above).
2) I am suggesting that this restriction on the Hamiltonian to 2-body terms is correct for the types of systems we consider for quantum computation. Clearly this is not something that can be proved mathematically, as it is simply a statement about physics. However, I believe this statement to accurately reflect our understanding of the physics of such systems.
3) I am suggesting that the consequence of 1 and 2 is that there exists a threshold on the total strength of spurious couplings a qubit experiences, below which high weight errors are suppressed exponentially, and hence periodic error correction can be used to suppress errors.
So that concludes my argument.
You may ask why your noise model doesn’t break this. I believe the answer is that your noise model cannot be written in this weakly coupled 2-body form. Note that I am not claiming that it cannot either be written with 2-body terms, or that it cannot be written with only weak couplings, merely that it cannot satisfy the two conditions at once.
Joe, regarding weakly coupled 2-body models, it is (AFAIK) an open question whether these models are compatible with our present best-validated microscopic models of quantum state preparation, a representative example being Metz and Beige’s recent “Macroscopic quantum jumps and entangled state preparation” (arXiv:quant-ph/0702095v4, 2007).
One concern of moderate skeptics is that generically observed qubit phenomena like “ relaxation” and “shelving” and “blinking”, which are well-described by Lindbladian dynamical models, are not known to be compatible with 2-body models in the weak-coupling limit … because the weak-coupling limit jointly constrains both the magnitude of the individual couplings and the number of such couplings.
relaxation” and “shelving” and “blinking”, which are well-described by Lindbladian dynamical models, are not known to be compatible with 2-body models in the weak-coupling limit … because the weak-coupling limit jointly constrains both the magnitude of the individual couplings and the number of such couplings.
Given the broad range of physics that is implicit in the notions of “ relaxation” and “shelving” and “blinking”, it’s difficult (for me) to imagine a formal mathematical demonstration, of the equivalence of Lindbladian dynamical models, with physically realistic yet weakly coupled 2-body Hamiltonian dynamical models, that would be simultaneously short, easily grasped, and definitive in its conclusions.
relaxation” and “shelving” and “blinking”, it’s difficult (for me) to imagine a formal mathematical demonstration, of the equivalence of Lindbladian dynamical models, with physically realistic yet weakly coupled 2-body Hamiltonian dynamical models, that would be simultaneously short, easily grasped, and definitive in its conclusions.
Here again a reference to a survey article formally demonstrating Hamiltonian/Lindbladian equivalence in a physically realistic weak-coupling limit would be very welcome. And if it should happen that this article’s analysis is short, easily grasped, and definitive in its conclusions, then reading it will be (for me and many folks) an Aaronson-style “thrilling adventure”! 🙂
Conversely, the (apparent) absence of such a definitive analysis in the present literature is a prima facie justification for moderate FTQC skepticism … in which event it hardly seems likely that the GLL/FTQC debate can reach any definite conclusion.
Joe,
Let me just quote the part of my above comment which explains why my model is not in contradiction with what you say on restrictions of relevant Hamiltonian models observed in nature:
“The idea is that if the evolution does not apply fault-tolerance to start with then this type of time-smoothing will not change much, so the smoothed noisy evolution will be a good approximation of the completely standard noisy evolution. However, this argument will break down for evolutions that exhibit the massive cancellation witnessed for quantum fault tolerance,”
Gil says:
I was thinking about your idea for detrimental noise, and it seems that your conjecture about this doesn’t have to be unique to FTQC. Your conjecture takes as “inputs” the natural noise processes and the control pulses applied by the experimentalist. If it held, wouldn’t we have observed it in other experiments, like spin echo, where control pulses are applied in the presence of decoherence?
First I want to thank Joe for his earlier useful comment.
and also Aram’s quote,
Thinking about the nature of noise in quantum systems is interesting, since our natural inclination is to view it as something external to our system.
There is a great point from Chapter 4 – Particles with Spin of Diagrammatica, pg 71,
One should really then look at Section 3.5 – Interpolating Fields
Which discusses the problem in relation to the inhomogeneous Kline Gordon equation (ref: http://homepages.physik.uni-muenchen.de/~helling/classical_fields.pdf)
along with the point on page 39:
So the schema for understanding noise in the system is to understand the problem in terms of QFT. The states of the system represent particles, and noise represents an anti-state (or anti-particle) that can annihilate a particular state. The information itself returns to “the vacuum”. The inability to retrieve the information can be thought of in terms of the situation where a particle and anti-particle annihilate, even though photons and neutrinos will be emitted, depending on the energies involved it might not be possible to determine the individual particles that where involved in the annihilation.
So jumping on John’s and Aram’s discussion, Lindbladian evolution is related to strongly coupled non-perturbative evolution. QECC can them be interpreted as creating well defined, strongly coupled families of particles so even if there is a random annihilation of one of the particles, if all are present in the initial state, annihilation of one member of the family will not lead to information loss (aside from an event that would annihilate all members of the family)
These leaves an interesting impression that strong fields are very survivable in weak fields.
I also like the relationship between iteration and perturbation. It seems that the break down does have some level of control in terms of relative strength up to the continuum limit.
Is quantum fault tolerance manifested in nature?
An interesting question related to the debate (and also a little to Joe’s argument) that we did not discuss is to what extent quantum fault-tolerance appears in nature. This is related to the medium interpretation of my conjectures that says that quantum fault-tolerance is not manifested for processes currently observed in nature (so my conjectures hold for them), but we can create systems allowing computationally superior QC’s to be built via quantum fault tolerance.
(This question has bearing on a question that was raised by Chris in the very first comment as well as by Boaz and others on “What is the computational complexity of our world, BQP? BPP? some other complexity class?” )
I have some comments based on the last few days of discussion.
Sometimes perturbation theory converges. In interacting quantum field theory, perturbation theory is at best asymptotic; it is spectacularly useful, yet has limitations when it comes to rigorously discussing issues of principle. That is part of the reason why my work on quantum fault tolerance has focused on noise models for which perturbation theory can be controlled. In [AKP], in Sec. 11 of [AGP], and in this comment, the noise Hamiltonian is a sum of terms, each of which acts on a constant number of system qubits and has bounded norm. In [NP] the bath is described by free (noninteracting) fields — that is, the noise is Gaussian. In these cases, we can rigorously bound the sum of all perturbation theory diagrams that cause logical decoding errors. That’s how we prove threshold theorems.
Two-locality is not sufficient. The noise model in [AKP] is two-local in the sense that each term in the noise Hamiltonian acts on at most two system qubits (though it may simultaneously act on many bath variables). That alone is not enough to ensure scalability, for a simple reason. Even if each term in the Hamiltonian acting on the pair of qubits (i,j) is very small, the sum over j of such terms for fixed i might not be small, and thus the single-qubit noise acting on qubit i could be strong. We need an additional convergence assumption. I called this “geometric locality” in an earlier comment, having in mind that if the interactions coupling qubits i and j decay sufficiently rapidly as these qubits separate in space then this convergence criterion will be satisfied.
Two-locality is not strictly true. Qubits are not elementary particles; they can actually be quite complicated objects, which may be why John Sidles (and Robert Alicki, too) emphasize the importance of dealing with renormalized qubits “dressed” by their interactions. But even if we consider them to be fundamental objects for the purpose of assessing Gil’s conjectures (as Joe and Aram seem to advocate), the interactions among qubits can be pretty complicated. For almost all applications of quantum field theory to elementary particle physics, we use an effective Hamiltonian with a short-distance cutoff, encoding all the virtual effects of quantum fluctuations at distances shorter than the cutoff. The effective Hamiltonian includes many-body terms, which are systematically suppressed by powers of the cutoff distance scale. For addressing questions of principle about the scalability of fault-tolerant quantum computing, these many-body terms cannot necessarily be ignored. That is why I considered a Hamiltonian with many-qubit terms here. For the proof of scalability to work in that model, the many-qubit terms need to be systematically suppressed, which is physically plausible.
A lot of my work on this problem has been motivated by a question similar to the one Gil asks. Can we reconcile highly controllable few-qubit systems with the failure of large-scale quantum fault tolerance? These noise models with weak many-qubit interactions may leave a little bit of breathing room for Gil’s conjectures, but not so much.
Lindblad equations are not fundamental. Markovian master equations are very useful in some contexts, but not necessarily the best way to address general issues of principle. Also, for the purpose of studying fault-tolerant computing, I don’t see the point of unraveling the master equation — it is actually easier to work with the Lindblad equation directly. I have not emphasized that approach much in my papers because I have the impression that skepticism of fault tolerance hinges on non-Markovian effects, while the Lindblad equation is Markovian.
Smoothed Lindblad evolution is not fundamental either. Or is it? Since Gil assures us he believes in quantum mechanics, just not in scalable quantum computing, I have assumed that he believes that the joint evolution of a quantum computer and its environment is unitary, governed by the Schroedinger equation with a particular Hamiltonian. (This is what I mean by a “Hamiltonian noise model”.) Then smoothed Lindblad evolution, a model with “intrinsic” decoherence, is an effective description of the noise in which the environment has been traced out. Comments by Aram, Joe, and me are directed at understanding the deeper Hamiltonian model, describing the interaction of computer and environment, underlying smoothed Lindblad evolution. Some of Gil’s responses have puzzled me, as he sometimes speaks as though smoothed Lindblad evolution is intended to be the fundamental description of the noise, not an effective description derived from the unitary joint evolution of system and environment. If that is really Gil’s view, he is more of a radical than I and others had suspected. If we are to debate whether quantum fault tolerance will fail because of a failure of quantum mechanics itself, new issues arise.
Whoops, the link [NP] was wrong in the above comment.
And still wrong when I tried to correct it. The correct link is [NP] (I hope).
Hi John,
You raise important points, and I didn’t mean to brush them under the carpet. This isn’t really my area of expertise, so I my have said something stupid at some point. However, let me respond to two of your points.
First, regarding your section point on two locality not being sufficient, I would like to point out that I was specifically requiring that the sum of all spurious couplings for each qubit be less than a critical value, which your counter example violates. (See this comment: http://rjlipton.wordpress.com/2012/03/05/the-quantum-super-pac/#comment-19359 ).
Your point about 2-locality not being strictly true is important. I know there exist systems in nature where this is not true, but on the other hand, it seems that virtually all of the interactions relevant to the construction of some kind of conventional quantum computer (i.e. ions in a trap or spins in a molecule) can be reduced to 2-local terms. Sure, we get effective higher order terms because because many of the couplings are often strong. I was suggesting that we imagine that we can make all of the spurious couplings weak. Perhaps I overstated the case for 2-localness, and perhaps it is showing a bias coming from the type of qubits I usually think about (spins or photons).
In any case, as I say, perhaps this is a flawed idea, but I think perhaps that it expresses what I feel is unphysical about Gil’s proposed noise model.
Also, I should say, I never really meant to reduce things to particle physics. Really, when I first mentioned the 2-local restriction, I had in mind dipole-dipole couplings, Ising couplings, hyperfine structure and the like in spin systems
Further, I know that the promise I require on the total coupling strengths is likely never to be satisfied in practice, since it means building a device you cannot simply hit with a hammer, but if we need to consider such noise, it seems we will never say anything definitive.
John, at least some forms of FT skepticism hinge not upon non-Markovian dynamics, but upon non-perturbative dynamics. The dynamical effects of greatest concern arise not in noise processes, but rather in measurement & control processes (the formerly being usefully regarded as an incidental subset of the latter).
The predilection of quantum system engineers (especially the quantum optics community) for Lindbladian models, in both unraveled and ensemble-averaged realizations, for purposes of modeling both noise and measurement & control, arises because this class of models naturally accommodates quantum processes that are non-unitary and non-analytic — jump processes and random telegraph processes for example — this being the class of dynamical processes that perturbation theory handles least well. Thus, two dual Great Truths of FTQC are “Lindblad equations are not fundamental” and “Perturbative expansions are not fundamental either”.
A natural question is, are non-perturbative noise/measurement & control processes incidental or fundamental to FTQC? The spectrum of opinion in this regard is broad, and at present the question is wide open, in the specific sense that no one can point to an existing survey of the math-and-physics literature that credibly concludes “This question is settled.”
Three remarks (and a question to Joe):
1) To Joe’s most recent comment
Joe’s proposal seems rather reasonable. I have one conceptual question to Joe:
Joe, don’t you require too much? Would it be enough if my noise model satisfied your requirement just for the type of quantum evolution we encounter in nature? (In particular, for quantum evolutions that do not enact quantum fault tolerance? ) After all, your restriction is not a consequence of quantum mechanics as an abstract theory but of the type of quantum evolutions we regard as “physical”.
The advantage of a noise model of the form I propose may be that it will explain the type of phenomenon (restriction of quantum systems) that you want to assume.
2) Censorship
One idea that we intend to examine next time is that natural quantum evolutions (and states) reflects bounded depth quantum computing. This looks related to Joe’s requirement from “relevant 2-local system”. Perhaps we can have a quick sanity check for this proposal before we move it to the front page.
3) Feynman’s motivation for QC
Regarding the discussion between John and Alexander regarding Feynman’s motivation. If indeed natural quantum systems do not enaxt quantum fault tolerance, this weakens the case for Feynman’s motivating idea.
Gil, I think for the (3) it is necessary define the “natural” fault tolerance first, e.g., that does “error (fault)” mean. But anyway, for one quantum system is more natural to mimic another one, than factor numbers. So idea of simulations looks less challenging.
I have some comments based on the last few days of discussion.
Sometimes perturbation theory converges. In interacting quantum field theory, perturbation theory is at best asymptotic; it is spectacularly useful, yet has limitations when it comes to rigorously discussing issues of principle. That is part of the reason why my work on quantum fault tolerance has focused on noise models for which perturbation theory can be controlled. In [AKP], in Sec. 11 of [AGP], and in this comment, the noise Hamiltonian is a sum of terms, each of which acts on a constant number of system qubits and has bounded norm. In [NP] the bath is described by free (noninteracting) fields — that is, the noise is Gaussian. In these cases, we can rigorously bound the sum of all perturbation theory diagrams that cause logical decoding errors. That’s how we prove threshold theorems.
Two-locality is not sufficient. The noise model in [AKP] is two-local in the sense that each term in the noise Hamiltonian acts on at most two system qubits (though it may simultaneously act on many bath variables). That alone is not enough to ensure scalability, for a simple reason. Even if each term in the Hamiltonian acting on the pair of qubits (i,j) is very small, the sum over j of such terms for fixed i might not be small, and thus the single-qubit noise acting on qubit i could be strong. We need an additional convergence assumption. I called this “geometric locality” in an earlier comment, having in mind that if the interactions coupling qubits i and j decay sufficiently rapidly as these qubits separate in space then this convergence criterion will be satisfied.
Two-locality is not strictly true. Qubits are not elementary particles; they can actually be quite complicated objects, which may be why John Sidles (and Robert Alicki, too) emphasize the importance of dealing with renormalized qubits “dressed” by their interactions. But even if we consider them to be fundamental objects for the purpose of assessing Gil’s conjectures (as Joe and Aram seem to advocate), the interactions among qubits can be pretty complicated. For almost all applications of quantum field theory to elementary particle physics, we use an effective Hamiltonian with a short-distance cutoff, encoding all the virtual effects of quantum fluctuations at distances shorter than the cutoff. The effective Hamiltonian includes many-body terms, which are systematically suppressed by powers of the cutoff distance scale. For addressing questions of principle about the scalability of fault-tolerant quantum computing, these many-body terms cannot necessarily be ignored. That is why I considered a Hamiltonian with many-qubit terms here. For the proof of scalability to work in that model, the many-qubit terms need to be systematically suppressed, which is physically plausible.
A lot of my work on this problem has been motivated by a question similar to the one Gil asks. Can we reconcile highly controllable few-qubit systems with the failure of large-scale quantum fault tolerance? These noise models with weak many-qubit interactions may leave a little bit of breathing room for Gil’s conjectures, but not so much.
Lindblad equations are not fundamental. Markovian master equations are very useful in some contexts, but not necessarily the best way to address general issues of principle. Also, for the purpose of studying fault-tolerant computing, I don’t see the point of unraveling the master equation — it is actually easier to work with the Lindblad equation directly. I have not emphasized that approach much in my papers because I have the impression that skepticism of fault tolerance hinges on non-Markovian effects, while the Lindblad equation is Markovian.
Smoothed Lindblad evolution is not fundamental either. Or is it? Since Gil assures us he believes in quantum mechanics, just not in scalable quantum computing, I have assumed that he believes that the joint evolution of a quantum computer and its environment is unitary, governed by the Schroedinger equation with a particular Hamiltonian. (This is what I mean by a “Hamiltonian noise model”.) Then smoothed Lindblad evolution, a model with “intrinsic” decoherence, is an effective description of the noise in which the environment has been traced out. Comments by Aram, Joe, and me are directed at understanding the deeper Hamiltonian model, describing the interaction of computer and environment, underlying smoothed Lindblad evolution. Some of Gil’s responses have puzzled me, as he sometimes speaks as though smoothed Lindblad evolution is intended to be the fundamental description of the noise, not an effective description derived from the unitary joint evolution of system and environment. If that is really Gil’s view, he is more of a radical than I and others had suspected. If we are to debate whether quantum fault tolerance will fail because of a failure of quantum mechanics itself, new issues arise.
Dear John, I thought my model which specify a quantum evolution based on a certain quantum operation at every intermediate time is completely equivalent mathematically to a Hamiltonian description on the system + the environment. Is isnt it correct?
Namely, I believe that my model is completely equivalent to a unitary, governed by the Schroedinger equation with a particular Hamiltonian for the qubits and the environment, and using quantum operations to describe it is completely kosher.
(Maybe I should not have used the word Lindblad, and perhaps the precise mathematics notations should be improved but the intention is to have a strictly kosher quantum evolution .)
Of course, I dont know what “fundamental” means.
Hi John
Let me descripe the general picture that I propose. Please let me know how your concerns from the last part of your comment refer to this description.
1) Universal quantum computers cannot be built (neither by nature nor by us). Modeling general purpose quantum computers in the standard way (or the way John P. proposes) is perfectly reasonable, but no matter how we engineer such a device the noise rate scales up and does not allow quantum fault-tolerance.
2) Special purpose machines for approximating pure-state evolutions can be built (by nature and by us). A machine required to approximate a pure evolution X depends on the evolution. Therefore the type of feasible mixed-state approximations to pure -state evolutions can systematically depend on the intended evolution. We try to find the fundamental laws for this dependence. What I call a smoothed Lindblad evolution (SLE for short) is indeed a proposal for this purpose. (my Conjectures 1-4 also serve this purpose.)
3) Yes, the description is equivalent on the nose to a Schroedinger equation with a particular Hamiltonian on the system and an environment. Mathematically, this is entirely within the realm of quantum mechanics. It is radical though, as the noise operation at time t depends on the intended evolution at all times before and after t. (We certainly cannot carry our mental picture and intuitions from the general-purpose case to the special-purpose case.)
4) For noisy quantum evolutions that don’t involve quantum fault tolerance the SLE description is very well approximated by a standard description. This is just a different way to do noise bookkeeping. But this is not the case for noisy evolutions that enact quantum fault tolerance and the massive cancellations occurring there.
5) The SLE description does not allow FTQC and therefore this description for special purpose machines for quantum evolutions support what we say in part 1): that universal quantum computers cannot be built.
> “Universal quantum computers cannot be built (neither by nature nor by us).”
To me, a computer science without computers feels very much like love without sex. 🙂
Gil writes:
I wish I had constructed my reply around this point, because it is a very concrete target.
What if I build a quantum computer, following the standard FTQC prescription, but I intend for the evolution to be the identity? Then SLE would be just like the original un-smoothed noise.
Less flippantly, “intent” is a ill-defined term, and even cleanly separating the system’s internal dynamics from the extra fields imposed by the experimentalist is not so easy.
And why would SLE occur only for quantum computers, and not elsewhere in nature?
Finally, when physicists talk about a Hamiltonian model, the Hamiltonian shouldn’t be time-dependent. Any time dependence should come from fluctuations or memory in the environment. Can you build a time-independent Hamiltonian that would yield SLE?
Hi Aram, your first point is very good. The reason the intent matters is because we discuss mixed state evolutions which are very near (in some sense) to a pure state evolution. Now, of course, the conjectures should apply to every approximated pure state evolution so the “intentions” are not important.
(Actually it will be nice to express this SLE evolution in terms of perturbation description for a pure state evolution.)
“And why would SLE occur only for quantum computers, and not elsewhere in nature?”
It should occur elswhere as well when we talk about mixed-state approximations to pure-state evolutions. When the evolution does not invole quantum fault tolerance the standard noise models are fairly close to this one. I think Conjecture 1 should follow from these SLE description and it does give concrete predictions in various situation.
“Finally, when physicists talk about a Hamiltonian model, the Hamiltonian shouldn’t be time-dependent.”
Ahh, you should have told me this before 🙂
This post of John [Preskill] is excellent in many ways, for which it deserves all of our appreciation and thanks. In particular, his post can be read as a roadmap for overcoming moderate skepticism, by a line of reasoning that we shall call “The Principle of Deferred Skepticism.”
————————–
Step 1: Accept that one can prepare a fixed, arbitrarily large number of qubits in the “zero” state.
Step 2: Accept that the computational evolution of these qubits is strictly Hamiltonian, and moreover the associated (time-dependent) computational Hamiltonian potential is strictly 2-local and deterministic-in-time.
Notice that Step 2 exploits Principle of Deferred Measurement (per Preskill’s notes). That is, all measurement processes are deferred to the end of the calculation.
Step 3: Accept that there is no additional source of noise during the computation — computational errors arise exclusively from imprecision in the realization of the deterministic-in-time Hamiltonian H(t).
Step 4: Accept that the FTQC threshold theorems laid out in Preskill’s notes are satisfied.
————————–
Now it remains only to measure the output qubits. There will be a lot of output qubits: perhaps as many as or more. But of course, most of them will be irrelevant ancilla qubits, that formally we need not measure (according to my imperfect understanding, anyway). Then a very interesting question is “Is there any room for reasonable skepticism regarding our ability to measure the output qubits in principle?”
or more. But of course, most of them will be irrelevant ancilla qubits, that formally we need not measure (according to my imperfect understanding, anyway). Then a very interesting question is “Is there any room for reasonable skepticism regarding our ability to measure the output qubits in principle?”
Here the point is that physical models of this final step introduce all the factors that have previously been cited as grounds for skepticism: we have to couple the output qubits to a quasi-continuum of far-from-equilibrium reservoir states; this reservoir coupling will “dress” the qubit states in ways that are difficult to calculate; the measurement operations necessarily will be realized as continuous Lindbladian processes rather than instantaneous projective processes; the Lindbladian generators associated to measurement in general cannot be assumed to be perfectly orthogonal, the physical of whixh ia that collapses are punctuated by jumps; jumps that are most naturally studied in unraveling formalisms (etc.).
In other words, assuming that our FTQC result has been successfully encoded in a highly entangled output state of dimension , it is natural to ask: is it scalably feasible to extract that information by realistically noisy, realistically Lindbladian, realistically nonorthogonal, qubit measurement processes?
, it is natural to ask: is it scalably feasible to extract that information by realistically noisy, realistically Lindbladian, realistically nonorthogonal, qubit measurement processes?
A practical advantage of this thought-computation (as it seems to me) is that it concentrates several grounds for FTQC skepticism into a single problem.
Do I have a strong opinion regarding the final result? Heck no! 🙂
… a key point is that although the output qubits are strongly entangled, that entanglement has the special property, that when the ancilla qubits are traced-out, the reduced density matrix associated to the
output qubits are strongly entangled, that entanglement has the special property, that when the ancilla qubits are traced-out, the reduced density matrix associated to the  output qubits is a near-perfect pure state — that scalable distillation being the point of the FT in FTQC Hamiltonian potentials. 🙂
output qubits is a near-perfect pure state — that scalable distillation being the point of the FT in FTQC Hamiltonian potentials. 🙂
John S. writes:
You have to be careful here. Under the standard assumptions of FTQC, at any moment in time, there are no qubits you can discard that will leave you in an approximate pure state. This is no different from FT classical computing in a model where bits suffer i.i.d. noise.
The only thing you can say about the information being present is that if you stopped the clock and ran a perfect decoding circuit, then the resulting state would be nearly pure (and highly entangled, or whatever else you wanted the ideal state of the system to be).
This is because the logical qubits don’t map in a 1-1 fashion to physical qubits; rather they are encoded as collective degrees of freedom, and “tracing out everything except the logical qubits” is equivalent to “applying a noiseless decoding circuit.”
(Why noiseless? Because we want to ask the question: is the information there, accessible _in principle_ by some operations.)
Love the video!
Aram, these questions are subtle, and I am no expert! I had envisioned that at the end of the unitary calculation the clock would stop (just as you say), and the logical qubits would be decoded back into physical qubits by a final unitary decoding circuit (just as you say), and that the concluding (non-unitary) measurement process would be sufficiently low-noise that most of the logical qubits would be read-out correctly.
John S.: Once we accept the Lindblad equation as a valid description of the noise, we don’t need to know the microscopic physics underlying the quantum jumps (which might be complicated) when we derive the consequences of the Lindblad equation. All I meant is, if the noise is weak enough (the jumps occur at a sufficiently small rate per unit time), then the proof of scalability of fault-tolerant quantum computation goes through. This is subject to the usual caveats, for example that jumps acting collectively on many qubits must be very rare.
You emphasize that correlations among qubit measurements could cause problems. (By the way, we don’t necessarily get around the problem by doing coherent processing until the final readout of the outcome of a quantum computation — to flush entropy we need to couple ancilla qubits to the reservoir and reset them, which could cause correlated errors even if we don’t read out the ancilla qubits.) Robert Alicki also raised a similar issue. Aram argues in his thought experiments that there is no reason in principle why we cannot make the correlations in measurements (or reset operations) very weak. That claim seems plausible to me.
Gil: Regarding smoothed Lindblad evolution you say, “Yes, the description is equivalent on the nose to a Schroedinger equation with a particular Hamiltonian on the system and an environment.” I’m sorry, this key point still eludes me. Could you re-express the SLE equation in the form of such a Schroedinger equation so I can see what this Hamiltonian is?
John asked: “Could you re-express the SLE equation in the form of such a Schroedinger equation so I can see what this Hamiltonian is?”
It looks to me that the answer is obviously yes. You look at the description in my paper (say, for simplicity, the discrete time description) which is given in terms of the intended evolution and the (smoothed) quantum operation describing the noise, and then every such description is equivalent to a Hamiltonian description for the qubits and the environment. (But maybe the question is not if this can be done in principle but rather a request to go ahead and make this translation so that we can see how the Hamiltonian looks like.)
Since I consider special-purpose devices (See point 2 in my comment) the Hamiltonian can depend on the specific device needed to approximate the intended evolution, and therefore the dependence of the Hamiltonian on the intended evolution can be more complicated than in John’s modeling for general-purpose quantum computers.
I guess one point that would come up in any kind of Hamiltonian formulation is some kind of “fat fingers” principle, in which it is impossible to perform a single-qubit rotation R without simultaneously affecting thousands of other (shadow) qubits with other rotations that are functions of R.
But more generally, I don’t think that the exercise of formulating SLE as a time-independent local Hamiltonian is just an empty exercise of formalism. For example, it would lead to requirements like the one I mentioned. Some of these requirements might not be compatible with certain implementation proposals, like linear optics.
Gil’s constraint is a good example of yet another Feynman aphorism:
So for fun, let’s pull the straps of a Feynman-style straightjacket as tight as possible in the context of FTQC … while still preserving concrete grounds for Kalai-style FTQC skepticism.
To accomplish this, let’s take “Hamiltonian description” to comprise four tight-strap straightjacket constraints:
(1) the Hamiltonian potential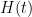 (of qubits + bath) is smoothly deterministic in time;
(of qubits + bath) is smoothly deterministic in time;
(2) dynamical flow on the state-space (of qubits + bath) is an exact symplectomorphism;
(3) dynamical flow on the state-space (of qubits + bath) is an exact isometry; and
(4) imprecision in the specification of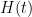 is fault-tolerant.
is fault-tolerant.
——————
Aside: radical variants of FTQC skepticism, as contrasted with minimal and moderate variants, retain constraints (1), (2), and (4) but relax the isometry constraint (3).
——————
Then Gil’s SLE receives a concrete and geometrically intuitive interpretation as follows:
(a) Specify the initial qubit density matrix as low-temperature thermal ensemble:
(b) Unravel as a Perelomov-style strictly positive P-distribution over coherent qubit states (note: exact closed-form algebraic expressions for this P-distribution are known).
as a Perelomov-style strictly positive P-distribution over coherent qubit states (note: exact closed-form algebraic expressions for this P-distribution are known).
(c) Conceive that initial coherent-state qubit distribution as a stratification of (rigorously) star-shaped domains immersed in Hilbert space, such that viewed as a high-dimension geometric object it is a “starry” distribution.
(d) By the Hamiltonian postulates (1)–(3), the final starry distribution differs only by a unitary rotation from the initial distribution.
(e) By the FT postulate (4), the center state of the final starry distribution is a product state of output qubits disentangled from ancilla qubits.
Then one well-posed geometric interpretation of Gil’s SLE postulate — which is rigorously consonant with the Feynman-style creative straightjacket of FTQC postulates (1)–(4) — is the purely geometric postulate that any finite-noise, finite-imprecision Lindbladian qubit readout scheme smears the final qubit readout data to be indistinguishable from the case that the qubit read-out is projectively exact, and the dynamical evolution had been SLE-type.
In this geometric view, an effective SLE dynamics is associated to the starry geometry of the initial qubit distribution, which is preserved throughout the FTQC computation, per the Feynman-style isometry postulate (3) above.
Now, is this geometric version of Kalai’s SLE postulate true? I will not venture so far as to assert that. But it is a well-posed geometric postulate, and it is perfectly feasible to conduct numerical experiments, broadly to gain insight into the coarse-grained SLE-type geometry of the final star-of-qubit-states, and specifically to see whether a geometric version of Kalai’s SLE postulate might perhaps be true, within a context that is both mathematically, physically, and technologically conformant to Feynman’s “creative straightjacket.”
And so this is what I am doing … mainly for fun … at a desultory pace! 🙂
Hmmm … alternative for the initial qubit thermal density matrix in the above post is:
for the initial qubit thermal density matrix in the above post is:
Such initial quibit density matrices are thermodynamically natural (obviously), and they have algebraically natural unravelings as positive P-representations, but as geometric objects these distributions become increasingly “starry” in the large-n qubit limit.
The intuition is that (perhaps) unitarily rotated starry distributions exhibit adverse error statistics under the unitary rotations that are associated to fault-tolerant processing of the ancilla qubits.
John [P], thank you for these helpful comments … in accord with the “Principle of Deferred Skepticism” … as applied in the context of a sincere effort to mitigate moderate skepticism … resetting ancillas during the FTQC process is not assumed (we simply use a lot of them instead). The idea is to ensure (in the language of geometric dynamics) that the following three FTQC elements are well-described as perfect symplectomorphisms and perfect isometries on the FTQC state-space:
(1) the starting “qubit denormalization process”
(in which qubits are decoupled from the reservoirs that initialize them), then
(2) the FTQC computational process itself, then
(3) the concluding “qubit renormalization process”
(in which qubits are recoupled to the reservoirs that measure them).
The resulting description ends up looking a lot like the accelerator physics associated to colliding rings. E.g. denormalization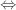 stochastic cooling, and QC gates
stochastic cooling, and QC gates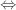 focussing elements. A key similarity is the requirement to preserve particle bunches/quibits as cold, controlled, and coherent over long periods of time; a key difference is that accelerator state-spaces are low-dimension compared to FTQC phase-spaces.
focussing elements. A key similarity is the requirement to preserve particle bunches/quibits as cold, controlled, and coherent over long periods of time; a key difference is that accelerator state-spaces are low-dimension compared to FTQC phase-spaces.
The goal of this mini-exercise is to summarize the strongest possible case for minimal, moderate, and radical FTQC skepticism (each independently), in the language of geometric dynamics.
As an aside, a valuable resource for this geometric/engineering way of thinking about the “FT” in FTQC is the Nion Corporation’s bibliography page Key publications on Nion microscopes and aberration correctors … see for example ““An electron microscope for the aberration-corrected era”, Ultramicroscopy 108, 179.
This references on the Nion webpage provide a reasonably definitive answer to Feynman’s celebrated question of 1959 (from his lecture There’s plenty of room at the bottom):
Perhaps nowadays we are similarly close to finding reasonably definitive answers to Feynman’s similarly celebrated question of 1981 (from his lecture Simulating physics with computers):
It seems evident (to me) that in neither case are the answers that we presently are finding likely to resemble the answers that Feynman and his generation of scientists expected! 🙂
Dear John, can you say, please, a little about the story related to Feynman 1959 question regarding electronic microscope? What was expected, what was achieved, etc.
Gil, a lot could be said on the subject of quantum limits to microscopy, both in the high-energy and low-energy limits! Feynman’s account in There’s Plenty of Room at the Bottom (1959) is as follows:
For in-depth STEM scholarship, a reasonable starting-point is Nicolas Rasmussen’s Making a machine instrumental: RCA and the wartime origins of biological electron microscopy in America, 1940-1945. As it eventuated, the electron microscope was developed largely to image the nanometer-scale pores in isotope-separation membranes … the program that was Feynman’s first assignment in the Manhattan Project … for this reason Feynman (and von Neumann, Dirac, Onsager, etc.) knew considerably more about the topic of microscopy than he was free to speak of (even today, much of this research remains classified).
For a QM/QIT/CT perspective regarding quantum aspects of Feynman’s microscopy challenge, see my own (brief) PNAS review “Spin microscopy’s heritage, achievements, and prospects“.
As for the final account of the quantum limits to microscopy — both practical and fundamental — well, that account remains to be written! 🙂
Thanks a lot, John
Reviewing John P’s paper [1] and Gil K’s paper [2], and thinking on conjectures in [3]. I wanted to highlight a worthwhile discussion in [4].
I would argue that the implication is that Lindbladian evolution is an effective approach only for an observer who’s total span is much smaller than the system’s.
It is important to also distinguish, at least qualitatively, the difference between the environment (Bath) that is an observer and an intelligence (Brain) that is an observer. In [1], good explanations of the difference between Markovian (no memory) and non-Markovian or InMarkovian processes (with memory). Since we are above the planck scale it is reasonable to think the noise is Gaussian.
So what differentiates the Bath as an observer and a Brain as an observer. I think the question does come down to an earlier post [5]. The most general Markovian Bath (M. Bath) follows the most simple and general process. The inclusion of memory in the InMarkovian Bath (I.M.Bath) implies that there is some process that is being followed that ensures the conservation of information (suggesting symmetry law and a gauge field). So that I.M.Bath is definitely process oriented, it will continue to process without regard to outcome. The InMarkovian Brain (I.M.Brain) it seems is qualitatively different in that it is interested in the outcome, it is more task or results oriented, it is only interested in process to the extent that it achieves a desired outcome.
Qualitatively, this reinforces discussion in [5] that nature does not deliberately circumvent an attempt to identify a better system.
More to follow.
[1] http://arxiv.org/pdf/0810.4953v1.pdf
[2] http://www.ma.huji.ac.il/~kalai/Qitamar.pdf
[3] http://rjlipton.wordpress.com/2012/01/30/perpetual-motion-of-the-21st-century/
[4] http://arxiv.org/pdf/0808.2096v1.pdf
[5] http://rjlipton.wordpress.com/2012/02/15/nature-does-not-conspire/
Continued.
Although there are some interesting comments possible about free will in terms of task selection, it is not the focus of this discussion so will be at least temporarily avoided.
In any case, all discussions on this topic should be in accord with the following statement:
Fundamental to this statement is a question about whether one can “observe” an entangled state. The answer to this question is yes and is related to our notion of wave-particle duality. The evidence is found in various experiments, but arguably it is seen in the variations of the double slit experiment.
The density matrix that contains all the information of a pure state. If we follow our argument that entangled states are observable and further add that they are bound states, then it is natural to associate a particle and a field to each entangled state. So every time one adds a basis vector to a density matrix, one is creating new fields in the off diagonal components. These could be included as basis in a new density matrix, which in turn creates new fields. This can continue to infinity (and because superpositions can be mapped to rational numbers, the infinity will be countable).
In order to aid in visualization, it is convenient to think of stretching the infinite size density matrix over the sphere. (example: http://www.geom.uiuc.edu/graphics/pix/Special_Topics/Topology/PlaneMap.html) One can imagine that the origin and the far corners of the density matrix joining and shrinking to a point on the sphere that simultaneously represents the origin and infinity. The states that are on the diagonal of the density matrix are now represented by a great circle around the sphere.
When one thinks about performing a measurement, for instance a two qubit system with basis:
|00> + |01> + |10> + |11>
One can imagine taking a sphere and making four smaller copies of it (represented by reducing the radius of the sphere). A measurement of the first qubit in state |1> leads to an annihilation of states |00> and |01> and leaves two spheres of the four remaining. Those two spheres now carry a constant state |1>.
When the second qubit is measured, one of the remaining spheres will carry either constant state |10> or |11>.
What is important in this example is that although I have “shrunk” the sphere by performing a measurement, because the sphere is of infinite order (but still countable), none of the information in it has been lost.
Now what happens when I impose a “cutoff” to the growth of the matrix? This would be represented by not allowing growth of rows and columns. In that case I can still construct spheres but they will be built from approximate “or flat” panels (in this case very reminiscent of http://www.geom.uiuc.edu/graphics/pix/Special_Topics/Topology/PlaneMap.html).
Each measurement will reduce the the number of segments, leading to a shrinking of the sphere again, until one gets to a final state, and the sphere effectively disappears.
This is a very different situation than the one before. In this case there is a definite loss of information as branching and splitting occur amongst the choice of successively smaller spheres.
This brings in the question about how to retain information on states when faced with a cutoff (as defined above)?
I am going to sign off for the evening, but again the natural answer is to look at the finite groups and retain the information through symmetry.
Let me try some Gedanken experiment. Alice want to send Bob a message. We prepare 3 independent streams (S1, S2, S3) of spin entangled electrons. Alice receives one electron from each stream, and Bob receives one electron from each stream. Now Alice want to encode a stream. She takes alpha particles and move them close to electrons from the streams S1 and S2 and measure S3 if she want to send 0, or close to electrons in streams S2 and S3 and measure S1 if she wants to send 0. Two things can happen, (1) due to electrostatic force electrons will be bounded to alpha particle to form He atom, but then due to Pauli principle bounded electrons will have opposite spins and third electrons would be independent from the other two. In this case Bob needs to measure correlation between streams S1, S2, S3. There would be perfect correlation in two streams, and no correlation between these streams and the third one. Moving Alice and Bob far apart this lead to superluminar information transmission. (2) Some kind of measurements during the capture that spins become classical with the measurement process not related to external bath – the system is pure QM, and then correlation lost before the capture. (3) Because there is no superluminar information transmission and this is more fundamental than electrostatic forces the capture is forbidden (until the effective measurement is performed ).
Some more philosophy,
I think this question of confinement can best be understood in a relative sense.
In a classical school room model of the expanding universe, we envision space (real space, not state space in this case) as being on the surface of a balloon. As the balloon expands, relatively unbound objects move apart. Bound objects generally resist the expansion and stay compact (so even if galaxies are spreading, people are still staying the same size).
Suppose we keep the surface area of the balloon constant? How do we represent objects moving apart? The answer is that we shrink the objects so that their angular size gets smaller. What about strongly bound objects? The answer is that they are shrinking faster then there relatively unbound cousins.
This should give one a sense of the relative degrees of confinement. This relative change in confinement does not appear to booth smoothly differentiable in our universe.
So the question comes down to one of interactions. (I have a horrible tendency to think of these things in terms of micro economics, but will avoid such allusions).
The central question is whether there is an intermediate or other action other than the two options of interaction or noninteraction?
One can think of exchanges between to entities in abelian and non-abelian terms. Assume Alice gives Bob some bits, if it is an abelian exchange, then Bob should give Alice back the same amount of bits. But suppose there is some cost (or benefit) to the exchange? Then when Alice gives Bob bits, Bob should be giving more (or fewer) bits back to Alice.
If we conservation holds, then there needs to some balance in interactions that cost and interactions that benefit.
So there is a hierarchy of options.
So our set of choices are: free fields vs. interacting fields, and abelian vs. non-abelian
So in our shrinking universe example, there is a break point that occurs each time someone adds a new set of rules governing exchanges.
As far as it relates to noise models, it is apparent that we can consider noise as being one side of a non-abelian interaction, aka a type of broken symmetry.
This relative change in confinement does not appear to booth smoothly differentiable in our universe.
Should be:
This relative change in confinement does not appear to be smoothly differentiable in our universe.
Just another note about this statement, I want to make clear that the manifold is smoothly differentiable, it is the objects embedded in it that interact which have non-smooth growths in the type of interactions (relative confinement).
Hal, it is well-established that seemingly non-dynamical changes in particle confinement geometry are associated to observable effects that are grossly dynamical: a recent experimental account is C. M. Wilson et al. “Observation of the dynamical Casimir effect in a superconducting circuit” (Nature, 2011) — the names Casimir, Moore, Unruh, and Hawking are among those associated to this (very large) class of incompletely understood quantum quasi-dynamical effects.
AFAIK, there is at present no literature associated to the intuition — which (AFAICT) is not obviously implausible — that quasi-dynamical quantum entanglement mechanisms, broadly belonging to the Casimir / Moore / Unruh / Hawking class, might be associated to the practical necessity of dynamically decoupling / coupling FTQC qubits from heat baths / measurement devices / cavity vacua.
This provides one more example of that rather large class of FTQC noise mechanisms for which it is entirely feasible, yet by no means easy, to “just start calculating.”
Thanks, absolutely agree to the point. I think to some extent one could control some of this through some of the symmetry considerations. Can one carefully control the energy going into and out of the system? I don’t know, but certainly shock control through mass damping might be an option.
Last note for now, it should be apparent that apparent broken symmetry is related to T-symmetry (time symmetry). This helps protect us from nonlocality above the planck scale.
So in our interaction analogy, if there is always a cost to interaction between alice and bob (where interest on the transaction is always positive) then the only conceivable way of restoring symmetry would be to have backward moving transactions that always have a negative interest rate.
So the ancillary qubits are definitely a necessity.
The question is whether there is adequate ability to predict the failure modes of the computer. Since there are finite components to the problem, it seems possible to have a larger portion of the system dedicated to failure prediction in the smaller system.
So the scalability will depend on the estimated rate of growth in failure modes. John P’s logarithmic growth expectation seems to be possible if we keep the system at a scale where we only anticipate weak interactions. I think miniaturization will be a problem though.
Rate of noise
Boaz: Is it really the case that standard noise models *assume* that the error can’t be brought below a certain absolute constant, or that they are just happy that they have the threshold theorem, but if instead of threshold an absolute constant the threshold would be 1/(log n) or maybe even 1/(sqrt(n)) they wouldn’t say it was physically impossible to realize.
This is a very good question. The TCS instincts would say that if the rate of the noise required for universal quantum computing behaves like 1/polylog(n) and perhaps even 1/poly(n) then this can be overcome. (Unlike, say, 1/exp (n)). But these instincts are quite problematic like various other intuitions transferred from digital computers to quantum computers. As Aram explained in his first post, noise rate of or so allows universal quantum computing without any quantum error correction. This implies that in order to demonstrate superior quantum computing it is enough to reduce the noise level below a sufficiently small constant. If you want to factor a 1,000,000 digit number with Shor’s algorithm it is “enough” to reduce the noise level per computer cycle to probably
or so allows universal quantum computing without any quantum error correction. This implies that in order to demonstrate superior quantum computing it is enough to reduce the noise level below a sufficiently small constant. If you want to factor a 1,000,000 digit number with Shor’s algorithm it is “enough” to reduce the noise level per computer cycle to probably 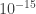 .
.
My conjectures suggest that the noise rate for noisy general-purpose quantum computers scales up (at least) linearly with the number of qubits. My papers contain some suggestions about lower bounds for the rate of noise for non-FT quantum evolutions (and this is related also to Conjecture C) but I think that understanding the rate of noise for non FT quantum computers should be further pursued.
If you consider quantum computers which allow arbitrary evolutions on k-qubits where k is very small, say, k=1, 2, 3, 4, 5 you can ask how the rate of decoherence depends on k. This is a very interesting, and we may get some insight from experimentalists rather soon.
Permanents vs determinants
Aram: “If you want to prove that 3-SAT requires exponential time, then you need an argument that somehow doesn’t apply to 2-SAT or XOR-SAT. If you want to prove that the permanent requires super-polynomial circuits, you need an argument that doesn’t apply to the determinant. And if you want to disprove fault-tolerant quantum computing, you need an argument that doesn’t also refute fault-tolerant classical computing.”
Aram was making a very interesting analogy. Of course, making analogies in general is a very tricky business, and there are various reasons why this particular analogy is problematic. But still there are a few lessons to learn here.
What is the principle that explain permanents being very hard to compute while determinant being rather easy?
To a large extent, this is the principle: “Permanents are hard while determinants are easy.” So unlike the case of, say, perpetual motion machines, in the permanent/determinant case the crucial thing was to offer the distinction between permanents and determinants itself as a fundamental principle, to propose a formal description and to build a theory based on it.
Similarly, the principle in our case may very well be: “quantum error correction (or quantum fault-tolerance) is impossible to implement while classic error correction (classic fault-tolerance) is possible.” Conjecture 1 expresses the quantum error-correction version and the smoothed Lindblad evolution are proposed to express the fault-tolerance version.
Two approaches for modeling
Scott: As Joe Fitzsimons pointed out, your conjectures about correlated noise seem constrained mostly by the goals of killing QC (or as much of QC as possible) while not killing classical computation — not by the goal of being consistent with what else we know about physics.
Joe’s point is indeed important, and some aspects of it were discussed over this thread. A central question is to choose between two approaches for modeling:
This leads to surprising “unknown physics” that we will be able to create by controlled quantum evolutions via quantum fault-tolerance. Joe’s 2-locality suggestions as well as John Preskill’s model represent this approach.
This is what I am trying to do. The conjecture is that an appropriate model for the behavior of special-purpose quantum emulators will demonstrate decoherence cannot be kept low for general-purpose quantum computers.
I would still insist on asking what prevents entanglement of 2 particles which are parts of other entangled pairs. In other words, do you need classical object to create entangled pair or it can be created in a small QM device. If you need only small device than it seems you allow superluminar information transmission. If you require classical device to create entangled pair, then what is the mechanism, and how big classical system should be to create entangled pair?
Three additional matters (not central to the discussion though).
Factoring
(Chris Moore, very first comment!) I am also a little confused by Gil’s motivation for his conjectures. It’s reasonable to take as a physical postulate (as Scott does) that NP-complete problems can’t be solved by a physical device in polynomial time… But I don’t see why the factoring problem deserves this status.
(Anonymous) The arguments seem to come down to quantum computers can’t exist because then factoring would be easy. Factoring is easy.
I beg to disagree. Factoring deserves high status. An efficient practical algorithm for factoring will be off-off-scale achievement. I don’t remember witnessing in my academic life any scientific/technological achievement so surprising. Therefore, any specific proposal for efficient factoring should be carefully and skeptically examined. (Regarding motivation, to the best of my memory, my main motivation for skeptically studying quantum fault-tolerance was that I thought that this is a direction worth pursuing and that I had a shot at it.)
Symmetry breaking and the aether
Aram wrote in his first post (slightly modified to make it less technical): “To reconcile Gil’s conjectures with classical computing as well as experiment, we would need to distinguish between bit-flip errors and phase errors. This is like theories of aether, in which dynamics have a preferred direction.”
As I note in this comment, it was a basic principle for me not to make any a priory distinction between bit-flip errors and phase errors (and also not to rely on geometry). However, let me also mention, that models of quantum computers which distinguish phase-errors from bit-flip errors can be quite useful even if we think (as I do) that the fundamental models should not make such a distinction. Also, I am not as negative as Aram to the theory of aether. It was the best explanation people could find for a long time for a variety of phenomena, untill a better explanation was found.
Metronomes and ion traps
Aram devoted some part of his second post to discuss metronomes. I am not sure how this part fits into Aram’s overall argument but at least I recalled the reason I mentioned them in my paper beside just being a nice example of “spontaneous” synchronization. In current implementation of ion traps we can expect that (phase) errors will have some periodic (in time) nature. The reason is that the least noisy ion trap qubits are not static but they have an internal Z evolution with known frequency. It is plausible that their Z evolutions are subject to some much weaker fluctuations of higher frequencies. My speculation was that this property in addition to the mechanism to control the location of all traps (and bring together the gated qubits at each computer cycle) can lead to a metronome-like effect for the errors.
Perhaps it is mathematically more accurate to say “Gil’s conjectures are like theories of protein folding, in which dynamical flows have stiff /curved directions and lax /flat directions.” Needless to say, for purposes of practical calculation, a non-flat non-static state-space affords tremendous advantages, even when we believe the underlying dynamical state-space is flat and static. Moreover, in the early 20th century, it turned out that even at the most fundamental level, classical state-spaces were in fact neither flat nor static.
Thus history shows us that intuitions in geometric dynamics that for many decades we regard as empirical and/or radical, can eventually come to be regarded as mathematically and physically natural.
John Preskill is entirely correct (IMHO) to assert that in this context “new issues arise”, and Jonathan Dowling and Gerard Milburn discuss these issues in a 2002 article:
When we integrate these Harrow / Preskill / Dowling / Milburn perspectives, we perceive that Gil Kalai’s class of conjectures have substantial pragmatic value in helping to equip us with the novel mathematical tools and physical intuitions that we need to “be in the right place at the right time” to realize the “key physical technological advances” that are essential to the liberty, prosperity, and security of the 21st century.
And, Gil’s ideas are fun. 🙂
“An efficient practical algorithm for factoring will be off-off-scale achievement. I don’t remember witnessing in my academic life any scientific/technological achievement so surprising. ”
Why would this be any more surprising that the AKS deterministic primality testing algorithm? Apart from it’s greater practical impact.
Hmm, this is a nice question. Probably in formulating the question I would first replace AKS by “Miller” because showing that primality is in P based on GRH is, from the point of view of the theory of algorithms, the crucial breakthrough. (And we generally believe GRH.) Easy factoring based on GRH or on any other conjecture from NT will be as sansational as unconditionally easy factoring.
Of course, Rabin’s and Solovay-Stassen’s probabilistic algorithms were great surprises on their own. This was the surprise in discovering the power of randomized algorithms, and also Rabin’s version is practically very quick. And then the Las Vegas and the amazing AKS derandomization were also theoretical surprises. But for your question the relevant issue is that primality is easy.
Primality being easy is a pleasant aspect of our reality and a source of many breakthroughs. Eratosthenes discovered a way to find primes much faster than people before him, in his part of the world. (Shortly afterwards humanity lost interest in primes for more than 1000 years.) There are excellent simple algorithms to find pseudoprimes of various sorts that were known from the time of Fermat (and much earlier to the ancient Chinese). I dont know how surprised were people with Eratosthenes but we can certainly ask around to find out how surprised people were with Miller’s algorithm (of course it was a great result), and how people regarded earlier evidence that primality is easy.
You can compare the case of primality to the pleasant reality (and source of endless theoretical discoveries) of solving linear equations being easy.
(I found this nice and readable article http://www-math.mit.edu/phase2/UJM/vol1/DORSEY-F.PDF on methods for primality by Zachary S. McGregor-Dorsey.)
So the situation for factoring feels quite different, although I am not sure we have good enough theoretical explanation for that (either coming from CC or from NT.) One “meta” reason is that the boundaries of feasible algorithms were much more flexible in the 70s and 80s when they were determined (often based on accumulated mathematical knowledge). And, yes, the great practical impact is a very big deal, which will make easy factoring an off scale technological and scientific event.
But certainly any specific proposal for efficient factoring (and even for less dramatic breakthroughs) should be carefully and skeptically examined.
I would recollect some theme that yet maybe was presented more or less directly in this discussion, but I did not see clear explanation about that. Conjectures 3 and 4 sound nonlinear for me, e.g., it might be considered as a claim that error events for entangled qubits differ from non-entangled ones. On the other hand, any entangled state is the linear combination of non-entangled ones. So it sound like the errors may represent some nonlinear process, if to consider the conjectures formally. So maybe it would be better to have some reformulation of those conjectures at least for “pedagogical” reasons.
Note: I am aware about “Brief Rejoinder by Gil Kalai on Correlated Errors and Entanglement”, but it is our classical intuition.
Note 2: To be precise, I am talking about amplitudes and linearity like
E(a|00>+b|11>)= a E(|00>) + b E(|11>).
It also would not be correct to say, what I am biased against the conjectures – I already mentioned that few years ago I was interested in an alternative encoding of qubit (in Hopf fibration) that would accept repetition codes without entanglement. So if the argument about problem with entangled error correction codes would be solid enough, such encoding even could devote an additional attention.
Alexander, with regard to your observation
that point can be usefully strengthened to
For example, today on the Arxiv server there appears Tian and Jing’s “How the Unruh effect affects transition between classical and quantum decoherences” (arXiv:1203.6141v1). With intuitions informed by Gil Kalai’s writings, it is natural to wonder whether the role of accelerated-frame vacua in regard to Unruh effects, might be played by the ubiquitous quasi-vacua of noise, measurement, and cavities in regard to the Kalai Conjectures … for example, in the practical context of input-denormalization / output-renormalization of qubits by external quasi-vacua.
More broadly, considerations like these help address questions that minimal, moderate, and radical FTQC skeptics hold in common: What key physical intuitions are associated to 21st century QIT? What proof / computation / simulation technologies are available? What new enterprises are feasible? What opportunities exist for individual researchers (students especially) to just start calculating?
The question of which side “wins” or “loses” the Kalai/Harrow debate has relatively minor significance, compared to the great global challenge of conceiving the broadest feasible span of illuminating answers to these questions.
Indeed, John, I simply mean, that it would be better to have at least one explicit formulation of the conjectures that avoid some (direct or indirect) challenges to axioms of quantum mechanics.
Hi Alexander. Thanks for the comments. Aram and I discussed a similar concern following his second post. (Indeed Aram proposed that the conjectures should be formulated in terms of shadow qubits which he discussed in the post, but I don’t see the need for that.)
Thank you, Gil. Indeed, the almost whole second part was related with similar topic. Yet, it seems to me that Aram used different representation (mixed state entanglement), there the topic with nonlinearity is more hidden and contradictory.
Comments by Scott
Scott’s comments in and regarding this debate were not technical or conceptual but polemic in nature. Still even with such comments he has a magic touch to raise interesting issues. Here are a few.
Simulating physics with classical computers
(Scott) An even more dramatic way to put the point is this: if quantum computing is really impossible, then we ought to be able to turn that fact on its head. Suppose you believe that nothing done by “realistic” quantum systems (the ones found in Nature) can possibly be used to outperform today’s classical computers. Then by using today’s classical computers, why can’t we easily simulate the quantum systems found in Nature?
Easily?!
What is the fast classical algorithm for simulating those quantum systems? How does it work?
This question (a similar question was raised also by Boaz Barak,) is indeed important. I have three things to say about it.
First, often the difficulty in simulating lies in our inability to make a good model and to learn various unknown parameters associated to a model, and not from the need of superior computational complexity powers. (Surely, superior computational powers will help…)
Second, note that Scott’s argument applies even if computationally superior quantum computers can be built but “realistic” quantum systems do not enact quantum fault-tolerance. Since we are not aware of any natural appearance of quantum fault-tolerance or quantum error-correction Scott’s argument does not require his assumption that “quantum computing is really impossible” and can be turned back to him.
Third, suppose that my proposal regarding smoothed Lindblad evolution has merit. (And we can put aside the question how fundamental it is, and even if universal QC can nevertheless be built.) Then this may lead to a conclusion (via some hard work) that realistic noisy quantum evolutions (or even just certain noisy quantum evolutions) admit a description by classical computers. Changing such an insight to a practical algorithm, may turmed out to be difficult and there could be even obstacles in principle.
(Scott) Like a wily defense attorney, the skeptics don’t even try to address such questions
I regard the analogy with a defence attorney as obliging, like also an analogy with a cryptologist who try to poke holes in a proposed crypto-system (I made the later analogy in my first paper). Let me comment that the questions Scott mentioned are discussed (briefly) in my papers and that in the last years these particular questions were addressed quite extensively by me in several discussions with Scott.
In thousand years, perhaps?
(Scott) for decades, a small but vocal minority of computer scientists and physicists has held that building a scalable quantum computer is impossible: not just really, really hard (which everyone agrees about), not just “impossible for the next thousand years” (how would anyone know?), but impossible even in principle,
Personally, I am more interested in an explanation that will work in thousand dimensions and I worry less about thousand years. (Also, as I said, I only tend to think that building universal quantum computers is not possible.) I am also quite interested to understand the nature of approximated pure states, and of noisy quantum systems before universal general-purpose quantum computers are built. (It will be nice to come up with such a theory even if it is going to expire eventually.) And we all need a good theoretical explanation for why QC are very very hard; once we see this explanation we can understand better if QC are possible or impossible.
(Scott) To date, though, no one knows how you can have quantum mechanics without the possibility of quantum fault-tolerance. So as I see it, the burden falls on the skeptics to give an alternative account of what’s going on that would predict the impossibility of scalable QC.
You bet!
(But maybe we should not insist that this will be accomplished in a single paper.)
Why, where, and what
(Scott) The question is: why does QC fail to yield a gain?
Because quantum fault tolerance is not possible (and is not witnessed in nature).
Scott (cont) Where does the breakdown happen?
There is no breakdown. It is not that something that is happening for a few qubits will stop happening for many qubits. It that something that we expect to start happening will not. The expected terrific phase transition which allows large quantum computers to apply quantum fault tolerance will not happen.
Scott (cont) What physical property of all realistic quantum states would be violated by the states that occur in Shor’s algorithm?
If you assume Conjecture 1, Shor’s algorithm is in troubles. It is unrealistic to have essentially noiseless (general) evolutions on a single (protected) qubit.
http://pra.aps.org/pdf/PRA/v70/i5/e052114.
page 052114-10.
“In other words, in this model with a finite separation, by changing the value of the magnetic field on the right side, it is possible to detect the effect on the left side nonlocally.”
A brave attempt to relate to the issue raised by John P. of what is the fundamental description of noisy quantum evolutions
John P. wrote: “Some of Gil’s responses have puzzled me, as he sometimes speaks as though smoothed Lindblad evolution is intended to be the fundamental description of the noise, not an effective description derived from the unitary joint evolution of system and environment.”
Let me repeat that my proposed smoothed Lindblad evolution description is intended as an effective (approximated) description derived from the unitary joint evolution of system and environment. But we cannot talk about “the system” and “the environment”. The system and the environment depends on the intended evolution (which, to a large extent, dictate the nature of the physical mechanism leading to this evolution). Of course, in nature there is no “intended evolutions” but you do have approximated pure evolutions and the proposal applies to them. (We may need at some point to transform the smoothed Lindblad evolution into a PDE or some asymptotic expansion which talk about approximations or perturbations of pure quantum evolutions.)
Regarding the various levels of fundamental descriptions of quantum evolutions in reality, the picture I have in mind is this:
First you have quantum mechanics: No geometry, no noise, no standard model, no specific laws of physics. This is the mathematical language for later levels of physics to be written.
Then noise enters. (Or thermodynamics, if you wish.) This is an additional layer of mathematical formalism which describes the nature of approximations in quantum mechanics. This layer is entirely and nonnegotiately written in the language of QM. Mathematically, everything can be described as unitary joint evolutions of system and environment. We still do not have any geometry and no specific laws of nature.
The correct description of noise does not allow quantum fault tolerance and universal quantum computers. This fact allows the emerging of geometry and specific laws of physics. This is why we can talk about different possible laws of physics where one set of laws does not enable to simulate others sets of laws.
And then we have our specific cozy laws of physics which specify our 3+1 (or whatever) physical world.
As usual, I agree with the points that Gil makes … while at the same time, it is evident too that the opposite point of view is similarly productive of good ideas. 😉
As usual, Feynman’s writings authorize to embrace this dualistic point-of-view. In his Nobel Lecture he reminds us:
As a concrete example, in this week’s PNAS Early Edition we find an article from Sean Barrett’s group at Yale titled “Phosphorus-31 MRI of hard and soft solids using quadratic echo line-narrowing.” Superficially, this article looks like a nuts-and-bolts description of bone imaging methods in medical research — which happens to be a special interest of mine — and yet we don’t read far into it before we discover the connection to fundamental FTQC research:
Mathematically speaking, is it best to appreciate the Yale goup’s work within a strictly algebraic, strictly flat, Hilbert space point-of-view? Or shall we appreciate it within a strictly geometric, strictly symplectic, product-space point-of-view? It’s pretty clear (as Feynman says) that we can appreciate this work fully only by appreciating it from every viewpoint.
Similarly, in regard to enterprise, shall we appreciate the Yale research as a diversion from the primary objective of (what Dowling and Milburn call) “The Second Quantum Revolution”, in which the demonstration of practical FTQC technologies is (as the QIST Roadmaps foresee, and as Scott Aaronson has recently wagered) “just a question of investment, time, and innovation”?
Or alternatively, is the Yale work representative of an emerging “Third Quantum Revolution”, composing a new class of quantum-based enterprises, whose technological objecives are envisioned concretely — for example, sustaining the yearly doubling of channel capacity that for five decades has yielded Moore’s Law improvements in MRI imaging sensitivity and resolution — whose pace is accelerating, whose risks are diminishing, and whose quantum foundations arise equally in geometry and algebra?
Fortunately, no-one has to choose between the now-maturing “Second Quantum Revolution” and the newly born “Third Quantum Revolution”: older and/or conservative-minded researchers can embrace the well-posed methods and objectives of the former, while younger and/or radical-minded researchers embrace the adventure and uncertainty of the latter! 😉
http://www.nobelprize.org/nobel_prizes/physics/laureates/1954/born-lecture.pdf
“The lesson to be learned from what I have told of the origin of quantum mechanics is that probable refinements of mathematical methods will not suffice to produce a satisfactory theory, but that somewhere in our doctrine is hidden a concept, unjustified by experience, which we must eliminate to open up the road.”
Mkatkov, that ‘s a very nice quote from Max Born. In respect to the Harrow/Kalai debate, we can read Born’s essay as authorizing and encouraging us to embrace a Third Quantum Revolution:
• whose mathematical foundations …
… are not in Hilbert space;
• whose physics foundations …
… are not in POVMs;
• whose algorithmic foundations …
… are not in matrix computations;
• whose flagship technology …
… is not FTQC;
• whose enterprise applications …
… are neither cryptography nor simulation;
• whose strategic focus …
… is neither long-term nor indefinite.
One very important, very positive, outcome of the Harrow/Kalai debate so far is that (as it seems to me) the terms of the debate helps to appreciate that the third quantum revolution already is far advanced … indeed, we can ignore the third quantum revolution only if we are willing to impose Procrustean/Bœotian restrictions on the terms of the debate.
John.
I have very basic problems with measurements and entanglement. I do not understand what is wavefunction collapse. Does it happen immediately, or it takes time. If we need classical device to measure via dephasing or whatever that should take time equal to the size of the required device divided by speed of light (I assume it is classical). That temporally extended process should be coupled with the process on the other end of entangled particles. So with enough precision in time (which depends on the required measurement device) we could affect dephasing of one particle due to interaction with another one remotely. I have a problem with the creation of the entangled pair. If, as assumed in EPR, entanglement can be archived locally by the QM device, than what prevent entangling of entangled particles. Do they have a special label? If nothing prevents that than superluminal transmission of information is possible – send two pairs of entangled particles one from each pair to Alice and another to Bob, entangle the unentangled pair on the Alice side and measure on the Bob side. Due to entanglement Bob will see correlations. Than to prevent superluminar transmission (should you?) of information either creation of entangled pair should be possible only by the classical device, or “measurement” should be possible in the quantum system. This is classical logic. May be in quantum logic you can avoid the study of the creation/annihilation of entangled pair, I do not know. If large system is needed to create the entangled pair than how large it have to be? What a physical expenses you need to put-in to produce large-scale controlled entangled system? Including the traces of the coupling to the environment that created this system.
And that is without talking about general relativity, which distort space-time.
Look, I do not need any explanations or replies, but “If you can’t explain something to a first year student, then you haven’t really understood it.”
Mkatkov, your questions are very reasonable. One reason they are hard to answer, is that they have many answers, that seemingly are very different, but (after what is sometimes quite a lot of work) can be shown to be equivalent. So here is *one* answer to *some* of your questions.
First, the physical process commonly called “collapse” is in fact a continuous process, and the mathematical tool for describing this process is called “unraveling”.
As a canonical example of unraveling, let us probe a qubit with a single, weakly interacting photon. To do this, we split the photon’s path in two, with an interferometer, and on *one* arm of the interferometer we scatter the photon off the qubit. In this process the outgoing photon on one of the interferometer arms picks up a state-dependent phase , which we assume to be very small, say
, which we assume to be very small, say  radians, with the sign depending on whether the qubit is “0” or “1”.
radians, with the sign depending on whether the qubit is “0” or “1”.
Now consider three fates of this quibit-entangled photon:
(1) We recombine it with the photon amplitude in the other arm. This describes the interaction as a weak measurement of the photon phase shift.
(2) We observe the qubit on each arm of the interferometer independently. This destroys the photon phase information, and describes the interaction as weak noise.
(3) We never measure the outgoing photon at all, in either arm of the interferometer … the quibit-entangled photon heads off into outer space. This option is called “Going to the Church of the Larger Hilbert Space.”
Then a key point is that we cannot distinguish, by any measurement process acting solely on the qubit, which of eventualities (1)-(3) actually occurred. Otherwise superluminal communication would be possible, in the sense that our (present) local measurements of the qubit would be affected by some (future) photon measurement process, conceivably occurring light-years away.
The mathematical expression of this equivalence principle is discussed at-length in Chapter 8 of Nielsen and Chuang’s Quantum Computation and Quantum Information. It is a lengthy but instructive calculation (that regrettably is not included in Nielsen and Chuang), to show that if one scatters many photons off a qubit, with each photon weakly interacting, then a coarse filtering of the aggregate data record yields precisely the projective statistics that are usually taught to students as representing “collapse.”
Summary: Many confusions regarding coarse-grained descriptions of quantum measurement can be resolved via fine-grained analysis of noise and measurement processes. A challenge for beginning students is not that there are too few such fine-grained analyses in the literature, but rather that there are overwhelmingly many of them … and yet, almost no introductory QM textbooks work through fine-grain details at a level that is sufficient to address the (legitimate) skeptical concerns of many students.
Question: Have the coarse-grained presentations of QM that became pedagogically popular following the success of the Feynman Lecture self-selected a generation of non-skeptical quantum physicists? That is a question for someone like Doron Zeilberger, not me! 😉
(as a follow-on to Mkatkov’s question) For example, in the above point-of-view, a measurement process is a physical process that is induced by interaction with a measurement device, and a measurement device is a machine that induces collapse by back-acting upon a quantum state so as to flow it toward agreement with the measurement.
This point-of-view naturally resolves the quasi-philosophical riddle — which is puzzling to many students — of why measurement processes act to collapse wave functions — it’s because measuring machines are *designed* to create processes that collapse wave-functions … designed either by human engineers, or alternatively, by Darwinian selection processes. ! 🙂
Similarly, this same point-of-view explains too why noisy and/or low-temperature quantum processes are generically feasible to simulate, and conversely, why quantum computers are so very difficult to construct—it’s because we are always free to regard Nature’s ubiquitous noise processes and/or thermal reservoir interactions as equivalent measurement-and-control processes, that act continuously to “collapse” trajectories onto low-dimension submanifolds (this is the process that Zurek calls einselection).
Thus FTQC seeks to accomplish two exceedingly delicate tasks simultaneously, first to reverse the ongoing dimensionally compressive flows that are associated to noise and/or thermalization and/or measurement, and second to reverse these compressive flows without introducing uncorrectable errors in the computational process itself. This is not a process that we observe anywhere in Nature, and is is natural to wonder whether it is feasible at all … which is why FTQC is such a fascinating research topic.
That makes me worry that simple system of coupled oscillators (I mean limit cycle non-linear oscillators with say stable radius, e.g. + what comes from Hamiltonian, and master-clock) can describe quantum computation (overall whole QM comes from waves). Unitary condition comes from fast relaxation to
+ what comes from Hamiltonian, and master-clock) can describe quantum computation (overall whole QM comes from waves). Unitary condition comes from fast relaxation to  , on Plank scales that can be violated. The only problem is modeling the measurement. I do not have precise constructions, but do not understand why that cannot be done. If there is no magic in measurement, we should have reasonable modeling tools for that.
, on Plank scales that can be violated. The only problem is modeling the measurement. I do not have precise constructions, but do not understand why that cannot be done. If there is no magic in measurement, we should have reasonable modeling tools for that.
Part of the construction can be: the quantum states |0> and |1> would be represented by orthogonal or collinear vector of the qubit oscillator coordinates relative to the master-clock oscillator. Nothing prevents this type of cubits to be in the mixed state, with amplitudes expressed by the projections to master-clock vector, and vector orthogonal to it.
Superconductivity x 3
I had a few off-line discussions (initiated by me) regarding the debate. David Deutsch had some remarks which I share with you (with David’s permission):
Superconductivity: Some remarks by David Deutsch
David offered superconductivity as a counter example to the strong principle of noise:
DD: Looking at the above link, though, I very soon ran up against your ‘Strong principle of noise’, namely
On the face of it, this principle seems to be violated by superconductors. For that matter, it also seems to be violated by individual photons as used in interferometry.
GK: I find it hard to believe that superconductors are counter examples. I suppose that superconductors are described by mixed quantum states which approximate certain pure states.
DD: I think a superconducting loop carrying a current is in a highly mixed state but a certain subsystem of it is in a pure state, to such enormous accuracy that it can be considered pure for all engineering applications.
GK: If this is so then this is a clear counterexample!!! (But I doubt it, can you elaborate?)
DD: I guess what’s needed here is someone who understands superconductivity at a fundamental (i.e. not just phenomenological) level. I’m not sure such people exist. I’m certainly not one.
GK: The reason I doubt that superconductivity (and superconducting qubits) is a counterexample, is that the only mechanism I am aware of in order to reach an essentially noiseless subsystem of a noisy quantum system (or specifically an essentially noiseless single qubit) is by quantum fault-tolerance quantum based on quantum error-correcting codes. I do not see how the experimental processes used to create superconductors apply such quantum fault-tolerance. Certainly these experimental processes can be described by a quantum computer that apply local quantum gates, but where is the fault-tolerance coming from?
We talked a little about Bose-Einstein condensation and it will be very interesting to discuss superconductivity in the context of Conjectures 1 and 2. (And also “individual photons as used in interferometry.”)
The stong principle of noise: a better formulation?
Here it is:
This is related to a long thread of comments over here (around this comment).
While we are debating: two exciting recent developments.
The first rudimentary quantum error correction in a solid state system
Steve Girvin mentioned to me a recent work of the group in Yale, with the first rudimentary quantum error correction in a solid state system! Congratulations! You can read about it here: At Yale, quantum computing is a (qu)bit closer to reality and the Nature article Realization of three-qubit quantum error correction with superconducting circuits, by M. D. Reed, L. DiCarlo, S. E. Nigg, L. Sun, L. Frunzio, S. M. Girvin, and R. J. Schoelkopf.
Will IBM build a quantum computer before Microsoft?
Another thing that happened while we are debating is: IBM Busts Record for ‘Superconducting’ Quantum Computer. Late February, IBM revealed that physicists at its Watson Research Center in Yorktown Heights, New York have made significant advances in the creation of superconducting qubits.
Sorry for naive question. There is should be the work on the self-consistent QM description of the free Hydrogen atom in empty space from the first principles. By the first principles, I mean that wave functions of the proton and electron induce distribution of charges, and this distributions are interacting with each other via electomagnetic field. Due to this interactions there is should be stable localized solution (since this is the intuition about Hydrogen atom). Does anyone know such a reference. Thanks. This is directly related to the above discussion, and in particular whether self induced fields (pure QM system) can create entanglement, and whether the QM description of the system is still linear, or like in general relativity it becomes highly non-linear. Thanks for any relevant references.
There is. It’s in every undergraduate physics course on quantum mechanics. See for example the wikipedia page on hydrogen-like atoms for an overview: http://en.wikipedia.org/wiki/Hydrogen-like_atom
Joe, that uses Coulomb V(r) as given from charge localized at the center of proton. But proton itself is a wave with its charge spread in space according to its wave function. Anyway thanks.
It’s simply in a frame where the proton is chosen to be static.
Joe, I do not see there the wave function of proton, even though it is static. That may be trivial, but I do not see it. That seems to assume singular in space proton, and spread in space electron – weird. It describes experimental observations, but still weird.
The wave function of the electron you calculate is not it’s absolute position, but rather it’s position relative to the proton.You are not assuming the proton is static relative to some other objects, you are simply calculating everything in coordinates which has the proton at the origin. The coordinate system is chosen such that the proton position is fixed.
Joe, you are saying that in this model the proton is not a physical object and It reveals itself only as a Coulomb field, and I’m rejecting to accept that unless it is shown as equivalent using two body problem. That is the reference I want to see.
That is not at all what I am saying. I have no idea how you could have gotten that from what I have said.
Perhaps a classical example will clarify the issue. The Earth (a heavy “nucleus”) and the Moon (a light “electron”) orbit one another. In an absolute reference frame both orbits are ellipses, with the major and minor axes of the Moon’s ellipse being about 100X larger than the Earth’s ellipse (in consequence of the Earth’s 100X greater mass).
In solving Newton’s equations, it is convenient to use (what are conventionally called) relative coordinates, referring to a single fictitious particle have a reduced mass, solely to escape the extra work of solving explicitly for two ellipses.
The usual Schrodinger equation for the hydrogen atom is no different — the coordinate given is the relative coordinate, and this coordinate implicitly encompasses the quantum wave-function of both the nucleus and the electron.
John, In Hydrogen model there is V(r) an external field. The system is closed there should be no V(r), or V(r) should be a function of wave functions of proton and electron. It is possible that this description could be reduced to external field V(r) with only one wave function, but than two entangled particles should also be possible to describe by only one wave function. In any case disregard my question, it seems that we are not understanding each other. I just want to see how two body problem of free electron and free proton in quantum mechanical world (not in classical world like moon and earth) can be reduced to standard Hydrogen atom model, e.g. how proton wave function is integrated out. Joe, sorry, I did not mean you personally, I was saying about the model. If proton is a physical reality it have to have wave function, or I’m again wrong?
Mkatkov, to be concrete, in the hydrogenic Schrodinger potential , the relative coordinate
, the relative coordinate  , where
, where  and
and  are respectively the (vector) nuclear and electron coordinates. Thus ordinary hydrogenic ground-state wavefunctions, e.g.
are respectively the (vector) nuclear and electron coordinates. Thus ordinary hydrogenic ground-state wavefunctions, e.g.  , do describe nucleon-electron entanglement, even though textbooks don’t commonly emphasize this (I hope the preceding LaTeX is OK!) 🙂
, do describe nucleon-electron entanglement, even though textbooks don’t commonly emphasize this (I hope the preceding LaTeX is OK!) 🙂
The wave function of proton and electron is separated using the same coordinates as in classical mechanics
using the same coordinates as in classical mechanics
 , e.g., Landau vol III.
, e.g., Landau vol III.
Ok, we solve it, and now I want to compute the distribution of positive charge. It should be consistent with our initial assumption. It is zero at the position of proton for , in the place we assumed all the positive charge is concentrated.
, in the place we assumed all the positive charge is concentrated.
I guess I have problem with interpretation. The image drawn here is consistent with pointwise protons and electrons interacting with Coulomb forces. It has nothing to do with the wavefunctions of either one. The wavefunction is a representation of probability of finding relative positions of two particles, which is more related to the measurement device, and not the system itself. I have very hard time to find another interpretation of wavefunction, consistent with hydrogen atom model. To give an analogy, suppose that we have probability distribution function of random variable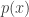 and a set of indicator function
and a set of indicator function  for Borel set
for Borel set  , than we can define kernel
, than we can define kernel  , and the probability of an event by abuse of notation
, and the probability of an event by abuse of notation  , than the question if the measurement device is able to represent an indicator function. If not, than we left with the option to approximate indicator function by
, than the question if the measurement device is able to represent an indicator function. If not, than we left with the option to approximate indicator function by 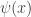 , so that
, so that  . Moreover, one can use resolution of identity, to estimate probability density function
. Moreover, one can use resolution of identity, to estimate probability density function  , where matrix
, where matrix  is density matrix of underlying probability and measurement device, and vector
is density matrix of underlying probability and measurement device, and vector  is the representation of a “state” of a device, and
is the representation of a “state” of a device, and  . No need for wavefunction collapse, and entanglement is a way to prepare the measurement device, and not the system (I’m exaggerating ).
. No need for wavefunction collapse, and entanglement is a way to prepare the measurement device, and not the system (I’m exaggerating ).
Sorry, latex went crazy, forget about it. All bra and kets disappeared.
I am not sure how it is related it is to mkatkoc’s question but I recall a very nice paper (the link is to a page which contains also computer programs and much data) by Christoph Koutschan and Doron Zeilberger redoing (using symbolic computation) a 1958 work by Chaim Pekeris who extended classic works on the hydrogen atom by computing the energy-levels of a two-electron atom. A naive question that I had when listened to the talk (and will be happy to read an answer) was if by now there are different computational methods for making these computations, if this can it be done for the case of more than two electrons, and if this is a case where quantum computers are likely to help.
Gil,
This might be something you already know about.
The cover story for the May 2012 issue of Scientific American is about a new approach for calculating quantum mechanical interactions called the “unitarity method” which is suppose to bypass some of the complexities of Feyman’s technique.
Dear Jim, thanks for the reference to the article.
I am vaguely aware (on a gossip level) of the recent miraculous simplifications of quantum field theory computations by Bern and others and related claims about the importance to physics. I guess, something even more basic that I am curious about is what specific examples are there for things that we will be able to compute via Feynman’s technique (simplified or not) and if the example of N-electrons atoms for N>2 is such an example.
If we need to choose between the three options:
1) Computations in quantum field theory that nature performs on a routine basis require superior computational power (and universal quantum computers).
2) There are miraculous computational simplification that allows efficient classical simulations a la Bern et. als.
3) These quantum fields computations, for realistic large problems, are computationally infeasible (by classical computation), and indeed the outcomes of the computation are simply irrelevant for these large problems.
I must admit that all these possibilities sound problematic. As important the new simplifications are (and I believe they are important) it sounds unplausible that they can make a computational-complexity difference. So I will regard the second option least plausible.
In any case, I am curious about easy-to-explain down-to-earth examples of problems that Feynman technique (with unlimmited computational power) can answer.