The Group Isomorphism Problem: A Possible Polymath Problem?
Can we beat the “trivial” bound on group isomorphism?
William Burnside was one of the founders of modern group theory. His classic book, Theory of Groups of Finite Order, helped lay the foundations. He proved some beautiful theorems, made some great conjectures, and in general helped start the modern era of group theory.
Today Ken and I want to talk some more about group isomorphism.
There was great interest in a possible attack on this problem. Perhaps it is a candidate for a Polymath Project. In any event looking at a precise conjecture is one of the best ways to make progress in any area of theory or mathematics.
Burnside did exactly this for group theory. He stated one of the most important conjectures in group theory, which was named after him. Suppose that 
Burnside’s Problem Specialized
Burnside found a neat way to develop his conjecture that also identified important special cases. The exponent of a group is the least common multiple of the orders of its elements, if it exists. If 
We can make an infinite group of exponent 2 by taking 
for all elements 
The case of exponent 3 is trickier, as not every such group is Abelian. Burnside himself resolved it in the positive: if a group of exponent 3 is finitely generated, then it is finite. Burnside was emboldened to put forth his conjecture:
For all
and
, if
is a group with
This is technically weaker than the general first statement we gave, because the latter could (and did) fail by having a finitely generated group with all elements of finite order but an infinite exponent. However, Burnside himself made his special conjecture even more concrete by defining a single group 
Disproved and Still Kicking
Just before World War II the conjecture was proved for 
However, Burnside’s original conjecture was refuted in 1964 by Evgeny Golod and Igor Shafarevich, who built an infinite group with three generators whose elements have finite orders that are unbounded powers of 
The problem is still kicking, however, because of Burnside’s concrete development of it. Cases for smaller
We wish to propound a problem that has some similar ingredients and special cases. Analyzing these cases may require some “heroic calculation,” but that may be structurable in a way that is good for a Polymath project.
The Group-Isomorphism Problem, Again
Recall that a group can be presented by giving the Cayley table: if a group has 
The problem is given two groups 
time by a deterministic algorithm. This method relies on the fact that any group of size 
Finite
A 
Let’s denote the number of groups, up to isomorphism, of order 
Related to this function is the folklore conjecture asserting that almost all finite groups are 2-groups: the fraction of isomorphism classes of 2-groups among isomorphism classes of groups of order at most 
Can we solve the Group Isomorphism Problem specialized to
Good News and Bad News
Several features of
The good news: The family of 
Here is a simple application of this principle. Any group of order 
The bad news: They can have large generators, as large as 
There is also the Burnside structure theorem on the generators of such a group: his theorem works for any
A Special-Case Problem
George Pólya had a principle for working on problems: when working on a hard problem, try to find a special case that captures its essence. I suggest that the best case to look at is the class of 
I think what we need is another strategy besides the generator approach. Let
Open Problems
Should we organize a Polymath Project? Ken and I think that we would help with one, but that we probably need at least one strong group theorist to help run such a project. Any takers?
Trackbacks
- The Group Isomorphism Problem: A Possible Polymath Problem … | Silcon Group
- Lipton Polymath Proposal: The Group Isomorphism Problem « The polymath blog
- Weekly Picks « Mathblogging.org — the Blog
- Giving Some Thanks Around the Globe « Gödel’s Lost Letter and P=NP
- DR KRUGMAN AND JOHN NASH JI – U KNOW – WHAT ? THAM CHICAGO BOYS ARE CALELD BOYS FOR A REASON – U GUYS KNOW RAHMBO OR NOT ? – DR KRUGMAN – RAMBO IS RAHMBO OR RAMBO – BUT ONLY ONE IS RAHMB « KATRINA KAIF TURcotte AJ
- The Speed of Communication « Gödel’s Lost Letter and P=NP
- Lucky 13 paper dance! | The Quantum Pontiff
- Mathematical Mischief Night « Gödel’s Lost Letter and P=NP
- Isomorphism Is Where It’s At | Gödel's Lost Letter and P=NP
- Three From CCC | Gödel's Lost Letter and P=NP
- Babai breakthru: graph isomorphism in quasipolynomial time | Turing Machine
- MO Polymath question: Summary of Proposals | The polymath blog
- The Lemma Cited From Burnside | Gödel's Lost Letter and P=NP
I very much like the sound of this project, but like you I feel that my group theory is inadequate. One thing I’d like to know is how to get a rich source of non-trivial 2-groups. Without that I have no way of assessing any algorithmic ideas. It would be particularly interesting to have two definitions of 2-groups that resulted in groups that were isomorphic but not obviously so — to get some kind of feel for the obstacles that an algorithm would have to overcome.
In general, the idea of a collaboration between group theorists, with their feel for what groups are out there, and computer scientists, with their feel for what clever algorithms are out there, sounds very promising, especially with this restricted version of the question.
Here’s one source of 2-groups: the finite quotients of the Grigorchuk group (which is a finitely generated, residually finite 2-group, which is typically constructed as an automata group). Because the Grigorchuk group acts on the infinite rooted binary tree, constructing families of such finite quotients is quite easy – just take the action of the group on the first n levels of the tree. More generally, many families of finite p-groups arise as quotients of just infinite pro-p-groups. See the book by Leedham-Green and McKay for more on this.
As for obstacles that need to be overcome, as well as more examples of p-groups, a very interesting paper in this direction is this recent one by Lewis and Wilson: http://arxiv.org/abs/1010.5466. They construct large families of p-groups (as quotients of Heisenberg groups) which have many invariants identical, but nonetheless they give a polynomial-time algorithm for isomorphism of these groups.
The groups discussed in Leedham-Green and McKay are the p-groups of bounded coclass. Perhaps there is a fast group isomorphism algorithm for these groups? There is certainly a much better understanding of the asymptotic structure of the class of p-groups of a given coclass than there is of the class of p-groups in general.
@Colin Reid: Indeed. As far as I know there is no efficient isomorphism algorithm for p-groups of bounded coclass (or perhaps you meant to suggest this as a potentially approachable problem?, in which case I agree.) Whether or not the p-groups of bounded coclass have an efficient isomorphism algorithm, it may still be a fruitful class of examples on which to test out new algorithmic ideas.
On the other hand, there are some reasons to believe that p-groups of class 2 may be the hard nugget of the isomorphism problem: 1) I recall that “most” p-groups are of class 2; related 2) the Jacobi identity of the associated graded imposes no condition in class 2, so their structure is in a sense less constrained than groups of higher class; 3) the isomorphism problem for class 2 is already “wild” (in the technical sense of the word). (Though wildness is only a rough and sometimes dubious indicator of computational complexity.) So perhaps some families of class 2 p-groups might be good examples on which to test new algorithmic ideas.
Back on the first hand: as you point out, we have a much better handle on the structure of groups of bounded coclass; so bounded coclass might be a better place to start.
Hmm, thinking about it, bounded coclass implies bounded number of generators, which is one case that can already be done in polynomial time. So perhaps not so interesting. Nevertheless, it might be possible to get a smaller degree than the general algorithm.
What about graph isomorphism? Are these connected problems? What do you think about?
Michael,
Group isomorphism is known to be reducible to graph isomorphism, but the reverse direction is not known.
Thanks, Joshua! 😉
I’m not sure that the fact that p-groups always have nontrivial center is *helpful*, except of course for the point about groups of order p^2. In fact, groups with no center are in some sense more rigid and thus might be easier to identify up to isomorphism. For example, because group extensions are classified by group cohomology with coefficients *in the center of the group* being extended, when the center is trivial the cohomology is trivial, making the extension problem potentially easier. That being said, it would be great for my intuition in this regard to be flipped on its head.
Whact exactly is “w” (or omega) in {0,1}^w?
This denotes the set of all strings of infinite length consisting of 0’s and 1’s.
I’m not a computational group theorist, but I know a few. From what I gather, there has been considerable work in (constructive) isomorphism problems for groups given as a generating set of matrices or permutations, and also for black-box groups. I imagine the last case is probably closest to what one would do with a Cayley table. The 2-groups case sounds difficult to me because there are so many 2-groups, and because the composition series tells you nothing.
PS: In group theory literature, ‘the isomorphism problem’ often refers to the problem of determining whether two group presentations (that is, as generators and relations) are isomorphic. This is probably not very useful for understanding the Cayley table isomorphism problem.
I have to wonder if this problem becomes easier if one has additional information about the groups. For example, what if one has representations of the groups over some reasonably small finite field? Similarly, every finite group has a faithful representation in GL(n,C). The Jordan-Schur theorem says that such a group must have an abelian normal subgroup that isn’t too small, and some versions of that theorem give explicit constructions. If one had an oracle that could give you some sort of information related to that. Say, given a group G, it returns the largest abelian normal subgroup (using some sort of lexicographic rule to decide which one to give if there’s a tie), does this make the problem easier?
In general it seems to me that since the real target of such a project is the full (multiplication table) isomorphism problem — that is, the problem for arbitrary finite groups — it might be worth attacking even this special case with an attitude that one is trying not to use the structure of 2-groups, but that if at some point it helps, then one will.
To put that a different way, there are two ways one might hope to find an algorithm in the 2-group case. The first is to get enough understanding of 2-groups that we can eventually find an algorithm. The second is to try to find an algorithm for general groups, with a view to understanding that problem well enough that we can see where facts about 2-groups could make things easier. The reality might be a mixture of the two, but I still have a feeling that the second is more promising.
Alternatively, we could try to make rigorous the intuition that p-groups (even p-groups of class 2) are the main source of difficulty in the problem. For instance, perhaps we can find an algorithm that runs in polynomial time given an oracle for p-group isomorphism, or perhaps even just an oracle to tell if the Fitting subgroups are isomorphic? Polynomial-time algorithms have been found for groups that are sufficiently far from being nilpotent, such as the case of groups with no abelian normal subgroups.
A problem which I’ve always found interesting is the following: A function f : {1,.., n} x { 1,…, n } -> { 1,…, n } is given, and it is a given that this is the multiplication of a group on { 1,…,n } – but beyond that, nothing is known; not even which element is the identity.
How many queries to f are needed to identify the group up to isomorphism and/or give the full multiplication table? The very naive bound is n^2, but depending on the factorisation of n very large speedups are possible. I’ve done a very small number of cases by hand, but it would be interesting to see how to do this for groups of 256, say.
Additional constraints on the group being guessed make the ‘game’ easier and would provide a measure of the information embodied in those constraints.
Jan de Wit
I am confused by your question. The function is the multiplication table, so what is to be found? The identity should be discoverable in O(n) time. What am I missing?
Well, look at Jan’s question in the “identify the group up to iso” version for small n. If n=1,2 or 3, the answer is that 0 queries are needed, because there is only one group of each of those sizes, up to iso. For n=4, 3 queries will do it, because you only have to distinguish C4 from C2xC2, and you can do that by asking for f(1,1), f(2,2) and (only necessary if those two turn out to be different) f(3,3). To distinguish the two possible groups, it suffices to look at the diagonal of the table, and 3 elements suffice because in C4 two elements occur twice each on the diagonal.Etc.I don’t know whether it is a useful approach to the problem you’re interested in, but if you can identify each of two groups up to iso you certainly know whether or not they are isomorphic!
I meant of course “(only necessary if those two turn out to be the same)”, sorry.
As I understand the question, the function is given as a black box, and you want to ask for as few values as you can and deduce the rest. So e.g. if n is prime, then you can solve the problem in time zero, since you know the group is cyclic. If n is the square of a prime p, then a very crude method to determine the group would be to test p+1 distinct elements and find out whether they all have order p, but there are probably better methods. And so on.
I find this quite an interesting question: given that the isomorphism question is hard, is it much easier to deduce the full multiplication table from just a few queries than it is to obtain some description of the group up to isomorphism?
Come to think of it, it’s not even obvious to me that there is some nice way to describe all finite groups up to isomorphism. Can it be done using CFSG somehow? That is, can we describe some product-type operations on groups in such a way that every finite group can be built up from simple groups in a canonical way? The reason I’m worrying about this is that for the examples I mentioned above the way I saved time was by using the fact that one can describe all groups of the given order.
As far as I understand it, describing the extensions of one group by another is really quite nontrivial in general. Although extensions are classified up to equivalence by an outer action and an element of second cohomology, this classifies them up to *equivalence of extensions*, rather than up to isomorphism of the total group.
Even if one were happy with that, the choice of element in second cohomology doesn’t need to be canonical, because the two groups in the extension can act as automorphisms of the second cohomology group, preserving the isomorphism type of the total group. (This, by the way, is not the only way two extensions can be non-equivalent but have isomorphic total groups. Thanks to Vipul Naik for teaching me that fact and showing me an example.)
On the other hand, maybe this is just the wrong way to go about it…
If finding descriptions for isomorphism classes of all groups is difficult, then that suggests that it is genuinely not feasible to solve the isomorphism problem by first saying what each group is and then declaring them to be isomorphic if you say the same in both cases.
What other possibilities does that leave? One is to show that groups are isomorphic or not without saying anything much about what those groups are. Another is to calculate a whole bunch of parameters and argue theoretically that any two groups that give the same answers must be isomorphic. The reason this is potentially easier than actually describing the two groups is that it may be that not all assignments of values to the parameters are possible. One way of looking at it is this. How can a bunch of polynomially computable descriptions be useful? Answer: if non-isomorphic groups have distinct descriptions and isomorphic groups have the same description. So we have a “description space D” and a map from finite groups (up to isomorphism) to D that we need to be injective. However, we don’t need it to be surjective, so this is weaker than a classification of all finite groups.
A slightly silly analogy would be that we don’t have a nice formula for generating primes, but it’s easy to distinguish between different primes because we do at least know that distinct primes are distinct integers.
Perhaps a related problem is easier to solve and still gives us some information.
PB: Alice knows the multiplication table of G and the goal is to communicate it to Bob. Alice gets to pick which m(G) elements of the table to send to Bob, such that Bob can reconstruct the rest.
There are two differences to what Jan de Wit asked: I dropped “up to isomorphism” and I let Alice decide what to communicate, rather than have Bob ask a sequence of “ab=?” questions.
Given the multiplication tables of G and H, an isomorphism checker could go like this: If m(G) differs from m(H) say false, otherwise do some $\Omega(m(G))$ work. Is there other information that comes from m(G)? Is it easy to compute m(G)?
(Incidentally, if Alice wants to communicate a partial order rather than a group, then I know how to pick what to communicate, but that seems of no help here.)
I’d be interested in such a project, but I certainly don’t qualify as an expert.
If we were to seriously attempt this, the first thing to do would be to rustle up a survey of properties of groups we know how to find in polynomial time, and generally try to summarise the current state of knowledge in a wiki or something. It does sound like the kind of problem where an incrementalist many-author approach could work. It’s not something I’d feel like I could say much about by myself, given my lack of knowledge of algorithms, but the whole point of the polymath approach is that we can get somewhere even if none of us understands the whole thing.
In fact, perhaps a lot of finite group theory is amenable to massive collaboration. I wonder, for instance, how much progress could be made on shortening the proof of CFSG (itself a many-author result) by a horde of relatively unspecialised people each looking at small pieces and making incremental improvements to them, without necessarily understanding the big picture. The existing proof is extremely long, but large parts of it consist of elementary arguments to eliminate this or that special case, and it may be that fresh eyes would see better elementary arguments. The more high-tech bits involving cohomology or character theory could simply be treated as black boxes. Even a significantly shorter proof of the Odd Order Theorem would represent a major achievement.
Colin, those achievements would be orders of magnitude larger. Moreover, while some parts of the proof certainly involve very elementary work, even those are long and involved and sometimes involve subtle issues. (This is my impression from the (small) bits of it that I’ve read). If one looks at for example Powell and Higman’s “Finite Simple Groups” which only contains some of the work that had been done up until 1970 one sees that there’s already a lot of difficult stuff.
Trying to improve the group isomorphism problem looks orders of magnitudes easier.
Yes, group isomorphism is likely to be easier to make tangible progress on, if nothing else because it hasn’t seen the same amount of effort poured into it as CFSG (especially the effort that has already been put into simplifying the proof in the last 30 years by the real experts). Then again, who knows how hard an open problem is?
I feel the exact opposite of what Colin feels: that I might be able to come up with a clever algorithm or two, but lack the expertise in group theory to know where to start, or what might be feasible, or to have any sense of what groups there are out there that need to be distinguished.
One possibility I quite like is that one might be able to determine whether two multiplication tables are isomorphic groups without being able to say much about what the group is or what properties it has — rather as you can sometimes say that two sets are the same size without knowing anything about what that size is. I don’t have any serious suggestions for how that might be done, however.
Does anyone know if graph isomorphism for connected comparability graphs has been shown to be in P? The reason I ask is that for a given finite group one has a few different almost natural partial orders of the elements which you can construct efficiently from the group table and are invariants of the group. For example, one could construct the almost partial order made by declaring x ~ y if x^n =y for some n. Then one identifies points x and y together if x ~y and y~x. This gives rise to a connected comparability graph in an obvious way (the graph is connected since the starting group is finite so every node is connected to the identity node). I don’t know in general any great examples of distinct groups look that have isomorphic comparability graphs, but that looks to be not very common. So if can solve that subcase of graph isomorphism that may handle a lot of groups.
Graph isomorphism is reducible to graph isomorphism for comparability graphs (i.e. comparability graph isomorphism is GI-complete). See for example http://www.cs.uwaterloo.ca/~dloker/papers/CS-2006-32.pdf and references therein.
Thanks. That rules out that sort of method pretty strongly.
Sounds like an adventure.
Count me in.
Sorry, one more thought: The graph isomorphism problem is solved for permutation graphs. Given a finite group G with n elements, one easily gets n permutation graphs (by looking at how each element permutes every element). If two groups are isomorphic then these sets of permutation graphs need to be isomorphic, and for two groups that can be determined in polynomial time in n. So this leads to two questions: are there examples of two non-isomorphic groups that lead to the same set of permutation graphs? (I suspect that the answer is yes.) Is there some reasonable niceness condition that isn’t too strict such that isomorphism of the permutation graphs implies group isomorphism?
Any element of prime order p must have its permutation graph as a union of cycles all of which have size p. So any two groups of the same order and prime exponent have the same permutation graphs.
A terminological note in case anyone wants to read more about this: this is essentially the approach of reducing a group to its corresponding “association scheme” aka “coherent configuration.” (Association schemes coming from groups are of course special.)
Also, any two groups which are distinguished by the orders of their elements are obviously distinguished by their sets of permutation graphs. Which raises a further question: what are some examples of pairs of groups not distinguished by the orders of their elements but which are distinguished by their permutation graphs?
Sorry, I was being silly before: it seems like the permutation graphs encode exactly the same information as the order of the elements. For a given element, the cycles in the corresponding permutation graph are exactly the cosets of the subgroup generated by that element, so they all have the same size, namely the order of the element. Or have I misunderstood what you meant by “permutation graph”?
Hmm, I’m not sure. It seems like you are interpreting it correctly somewhat (relevant Wikipedia article on permutation graphs http://en.wikipedia.org/wiki/Permutation_graph ) but I don’t quite see how the permutation graphs are encoding only the order of the elements. I see why it includes that information but not why that’s precisely it. What am I missing?
Hold on, I don’t think this makes sense — permutation graphs are derived from a permutation on an ordered set of elements; it’s not enough to just know the cycle type of the permutation. (Of course, knowing the cycle type in this case is the same as knowing the order!) There’s not a natural total order on elements of a finite group, so you won’t get permutation graphs unless you choose one, but that defeats the point.
For instance, if our group is C_4 with generator g, then the order (e,g,g^2,g^3) yields an empty graph, two Y’s, and a cycle. But if we order it (e,g,g^3,g^2), we get an empty graph, two paths, and a complete graph. So this isn’t an invariant.
Perhaps this is fixable if you take some natural partial order and require that the total order used extend it somehow and then it’ll be an invariant? No idea.
Oh hmm. You are right. For some reason I sort of assumed that permuting the order of the elements would give you the same set of permutation graphs to work with, but that’s not the case. This idea fails pretty miserably.
Given the number of references to graph isomorphism in the current discussion already, I was wondering why we are tackling the Group Isomorphism Problem and not the Graph Isomorphism Problem.
I followed the pointer back to “An Annoying Open Problem” and copied this section:
*******
The Short History
I find this problem very annoying. I have spent uncountable hours working on this over the last decades, especially jointly with Zeke Zalcstein. One reason the problem is so annoying is that it is easy to prove that it can be reduced to Graph Isomorphism (GI). But surely the additional structure of groups must help make the problem much easier to solve. Here are some encouraging differences between groups and graphs:
Every subset of elements of a graph is a graph; only certain subsets of elements of a group form a group.
Groups have a tight structure that varies with the prime factorization of , the number of elements. For instance, if is a prime there is exactly one group—the cyclic group .
Groups always have automorphisms, provided . Graphs can have many automorphisms—for instance the complete graph has —or they can have as little as no nontrivial automorphisms.
I could go on and on with the many structural differences.
***********
I suspect we are looking at some hard earned wisdom about the problem and we should take advantage of it.
The first and foremost item about “subsets” is somewhat curious:
Are Graphs somehow more consistent and less Russell paradoxical than Groups? Is there an asymmetric anomaly with Groups that we can exploit?
The definition of groups as sets with binary operations G^2->G, can be generalised to sets with n-ary operations G^n->G (Dornte, Post, et al), or even n,m-operations G^n->G^m (Cupona et al) satisfying group-like axioms. Finite n,m-groups only exist if n>=2m.
Can you say something about n-group or n,m-group isomorphism problems on their n-dimensional multiplication tables that enables you to say something new about 2-dimensional group tables ?
“n-GROUPS IN THE LIGHT OF THE NEUTRAL OPERATIONS”, Janez Usan, 2006, http://www.moravica.tfc.kg.ac.rs/Special/n-Groups_in_the_Light_of_Natural_Operations-v2006.pdf
Here’s a very naive approach to the problem, which clearly fails (or the problem wouldn’t be open). Suppose you fix some smallish integer such as 100. Then given two groups G and H, you can in polynomial time run the following algorithm. For each sequence
of 100 distinct elements of G and each sequence 
of 100 distinct elements of H, check whether the map that takes 
to 
extends to an isomorphism of the subgroups they generate. If they do, then join the corresponding sequences by an edge in a big bipartite graph.
If G and H are isomorphic, then this graph must have a perfect matching (just join each point in G to its image under the isomorphism), and this too can be tested in polynomial time.
So my obvious question is this: what are some examples of pairs of non-isomorphic groups G and H and functions
such that if you take 100 elements of G and their images in H and look at the subgroups they generate, you always get an isomorphism?
Sorry — I misstated the “obvious question”. I mean of course that there should be a correspondence between the sequences of length 100 — getting it to come from a map f such as I described above would give you an isomorphism.
Tim (gowers),
I cool idea. The number 100 could be even a small constant times log n and still improve what we know. The issue of course is: can two groups be not isomorphic and stil have the same “subgroup” structure? I do not know the answer to this question? Will think about it, of course.
I realize I’ve still not stated the question very well. The bipartite graph isn’t all that interesting, since it consists of an edge-disjoint union of complete bipartite subgraphs. So finding a matching doesn’t need any cleverness at all, and the entire point, as you basically say, is simply a generalization of counting how many elements there are of each order, which is what you’re doing if you take 1 instead of 100. Even taking just pairs of elements would be nice to know about, since that will trivially distinguish between Abelian and non-Abelian groups, so it seems to be much more powerful than counting orders.
Doesn’t this reduce to a question about the length of non-trivial relations in the two groups?
If the two groups differ only in that they each have some relation using more than 100 distinct group elements, and those relations are distinct from each other, it should be possible that the set of subgroups with 100 generators are equal for both groups.
I don’t have an explicit example at hand but I believe that it shouldn’t be too hard to produce one by constructing two groups in terms of their group presentations.
I agree with your second paragraph but the first sentence is misleading: it’s not the length of the relations that matters but the number of distinct generators involved.
Actually, I’m not quite sure that I agree with the second paragraph after all. It could be that every relation in one group holds in the other as well, but the number of times it holds is different for the two groups. That is what is tested for by the simple-minded algorithm I suggested. (For example, with k=1, the algorithm doesn’t just look to see which orders of elements occur, but also how many elements there are of each order.)
I basically agree. What I had in mind was only an example of a situation where the algorithm with a fixed value of k, e.g. 100, would fail to distinguish the two groups.
In general the algorithm will find all “short” relations between group elements, where short means that the number of distinct elements involved in the relation is at most k, and also count the number of times such relations appear.
One problem is that for many groups there will be distinct pairs, and other small tuples, of generators which actually generate the full group and for such pairs we are lead back to the problem of deciding if two groups of the same size are those we started with are isomorphic.
That last problem isn’t a problem. If a group is generated by two elements (a,b) then we can test easily for isomorphism with another group by checking all possible pairs of elements (c,d) of the other group and seeing not just whether they generate isomorphic groups but whether the function from a to c and b to d extends to an isomorphism.
That is true. This is is a simpler subcase of the isomorphism problem.
As Dick pointed our earlier this algorithm type has a reasonable running time for k = c log(n). Are there any good examples where the value of k needs to be polynomial in n in order to distinguish the two groups?
That’s not quite what Dick pointed out. If
for a small constant 
, then the algorithm does better than what is known, but is still superpolynomial. For it to be polynomial, then 
has to be bounded. It never needs to be more than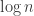 
, since every group can be generated by 
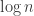elements.
Doing better than the best known algorithms would be a good first step, and probably easier than actually finding a polynomial time algorithm. So even a small value of c looks worthwhile to me.
You are right about never needing a c>1. I’m misleading myself by thinking about the possible sizes of the generated subgroups.
This seems relevant:
http://www.springerlink.com/index/t720732514k180j0.pdf
although my German is not quite up to it. “Lattice of subgroups” seems to be the right search term, and at any rate, two groups can have isomorphic lattices of subgroups (which implies they’ll pass the test here unless I misunderstand, which is quite possible?) without being isomorphic; indeed, one can be Abelian and the other not.
[How does one comment here without one’s comment languishing for days in “awaiting moderation”? Trying to see if FB login is better than what I did before…]
I don’t think it’s the same as having isomorphic lattices of subgroups, because we’re interested in what the subgroups are as well as what the containment relations are. In particular, if one group is Abelian and the other not, then k=2 is sufficient to distinguish them, because one group will contain a pair (x,y) such that xy doesn’t equal yx, and the other won’t. (What would be tested for is a 1-1 correspondence between ordered pairs of elements in such a way that if f(a,b)=(c,d) then the function that takes a to c and b to d extends to an isomorphism.)
Of course, sorry. Still, maybe this, from Max Horn writing at MathOverflow
http://mathoverflow.net/questions/35455/does-subgroup-structure-of-a-finite-group-characterize-isomorphism-type
is still interesting: “there are finite non-isomorphic groups G and H such that there exists a bijection between their elements which also induces a bijection between their subgroups.” Indeed the example given at the source has corresponding proper subgroups being isomorphic (that’s me saying that, not him, but seems easy. GAP has a LatticeSubgroups command btw, although that post didn’t use it.) The example here has G and H being different semidirect products of C5 with (C11xC11). I don’t know whether there could be an example which was a p-group.
IMHO: A key to the ISO-Group problem may be the relationship between group isomorphism and graph isomorphism.
Why are graphs less structured and more amorphous than groups?
Is there a meta-language that captures the difference?
The best known algorithm already takes advantage of the extra structure, namely generators. Indeed it gives a quasipolynomial time (n^log n) algorithm for group ISO, whereas the best algorithm for graph ISO is n^\sqrt{n}.
I am most definitly not a pro at this and I do feel somewhat silly entering this conversation because of that, but my curiosity has become far greater than my timidity. I’m not too aware of the rules behind the use of superscript and subscripts in computation and informational display, but it does seem like there’s a great deal of unused potential there.
Taking graph Isomorphism, because I believe I understand the relationships in those problems better; assume two graphs with 4 vertices. The first is a tradidtional square, the second a triangle with the bottom edge split in half by the fourth vertex. G= V={1,2,3,4) E={{1,2},{1,4},{2,3},{3,4}} ; H= V={A,B,C,D} E={{A,B},{A,D},{B,C},{C,D}}. Using vertex 1 from graph G as an example, 1 has a degree of 2, so it would be 1sub(2), Then to try and establish the connections, add one of it’s connections as a superscript, so 1sub(2)sup(2). That would be enough information though, so you would want to add vertex 2’s degree value for 1sub(3)Sup(2sub(2)). From there you can add the next connection in the same way. 1sub(3)Sup(2sub(2))Sup(4sub(2))using the capline, midline, and baseline. Once this is done for all vertices of both graphs, the vertex labels can be changed to 1. This would make the previous example 1sub(3)Sup(1sub(2))Sup(1sub(2)). Call this a vertex relationship.
If the two graphs are Isomorphic, you should be able to use a set cover method by using all 4 vertex relationships from graph G as a set universe, and each vertex relationship, individually, from graph H as the problem’s sets. If there is a cover for the universe set, then the graphs are isomorphic.
I don’t know if this is an acceptable use of subscripts and superscripts and I’m not sure how this relates to group isomorphism, but I’m very curious as to both.
Bah, typoed the example of the vertex relationships, and thats why you don’t read from paper experiments when typing up different examples.
It should be 1sub(2)Sup(2sub(2)), 1sub(2)sup(2sub(2))Sup(4sub(2)), and 1sub(2)sup(1sub(2))Sup(1sub(2)).
Here’s a question for group theorists. How many groups of order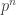
with at most 100 generators are there? I read that, being a bit rough about it, the number of groups of order 
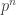is sort of like 
. If the number generated by at most 100 elements is 
, then the number of “subgroup profiles” (by “subgroup profile” I mean the multiset of subgroups generated by 100 elements) is at most the number of ways of writing 
as a sum of 
non-negative integers, which is at most 
. So if 
is substantially smaller than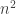 
for large 
(which feels a bit optimistic), then by a counting argument we get two non-isomorphic groups with the same subgroup profiles.
I don’t think this argument has any chance of working.
In fact, it doesn’t work, but let me at least record the failure here. Even Abelian groups are too numerous for this crude approach to go through. The number of Abelian groups of size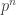
with four generators is at least the number of ways of writing 
as a sum of four positive integers, which is definitely bigger than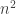 
.
So that suggests to me that a counterexample to my original question (to find two non-isomorphic groups with the same subgroup profiles) would have to be clever constructions rather than generic examples that arise from the fact that there are so many
-groups. I could have slipped up somewhere though.
How about finding metrics to turn the set of groups of order n into a finite metric space M, such that d(G,H)=0 iff G is isomorphic to H, and then find polynomial-time algorithm to check d(G,H)<=k for some k, and then incrementally try to improve this upper-bound until k=0. If w is the diameter of M then you already know d(G,H)<=w.
"Finite Metric Spaces & Their Embeddings:Introduction and Basic Tools", Manor Mendel, CMI, Caltech, http://www.cs.caltech.edu/~schulman/Courses/0405cs286/manor-lec1.pdf
A vague and probably hopeless thought. Might there be a way of proving that if graph isomorphism is very hard then group isomorphism is at least quite hard? To do that, one could attempt to construct a group out of a graph in such a way that non-isomorphic graphs gave rise to non-isomorphic groups. Even if the groups were quite a bit larger than the graphs, a big lower bound for graphs could have non-trivial consequences for groups.
The difficulty with this approach is that the obvious ways of converting graphs into groups (such as, e.g. letting vertices be generators and associating relations with edges in some way) produce groups that are much too big, or even infinite. Getting something cleverly compressed looks as though it could be formidably difficult if it’s possible at all.
I think you have identified a viable possibility.
Graph Theory already has a clever way of compressing things called “vertex reduction”.
One trick Graph Theorists do not seem to have exploited much is making mutually exclusive, simultaneous vertex reductions.
Jim,
This is an interesting idea. I once used it in a completely way to color planar graphs. See this.
Dear Sir,
I am curious. Is there a word missing in this sentence?
“I once used it in a completely way to color planar graphs.”
The pointer to the paper was quite interesting. My strategy for five-coloring maps at the time that paper was written was to construct a large chain of two-colorable countries, view the group as a single country (a reduction group), and then three color the bordering countries.
One heuristic trick for linking chains with the same two colors that could not be reduced to a single country was to use four sided “bookkeeping” countries. It was one of my “Your Cheating Heart” algorithms.
The problem with bookkeeping countries is it gets very tricky keeping track of them and they “will tell on you”, if you get careless.
Back to the task at hand and following up on Tim Gowers’ idea:
Why not view the vertices that comprise a connected graph as a peer group of functions where f, g, and h are three vertices:
1. f(f) = 1, the identity function.
2. f(g) = 2, if the vertices g and h are connected by an edge.
3. f(h) = m, where m is the number of vertices in the reduction group that includes all the shortest paths between f and h.
If you and Tim find the idea amusing, I have a zillion tricks for implementing peer reduction groups on planar graphs that may be useful for any 2D surface with a finite genus.
It might be useful to begin with a limited number of vertices with an upper limit on the genus of the surface. It should greatly simplify things until we can get the algorithm up to a reasonable speed.
We can worry about 3D spaces later.
Correction:
#2 should read: f(g)=2, if the vertices f and g are connected by an edge.
Haste makes waste.
Never mind the peer group thing for now:
#1 is not right either.
Hi guys,
I know nothing about groups, and looking at multiplication tables for small groups. http://www.math.niu.edu/~beachy/aaol/grouptables1.html The observation is if one look at 2×2 minors only, and look only at minors containing 1 on the table diagonal, one can easily get generators and their multiplicities. The procedure will be for each minor with 1 on the table diagonal find the same minor, and list the rows and columns it appear as 4-tuple, than look at the chain of tuples, where the chain consist of connected tuples, e,g, tuples containing at least one common elements. The longest chains containing 1 are corresponding to generators. Moreover, I suspect that the relations between generators are also encoded in a relatively simple way in chains of 2×2 minors.
I guess the problem is not in finding generators, but in finding the relations between them.
mktakov:
I think you just nailed the idea I was mangling:
“I guess the problem is not in finding generators, but in finding the relations between them.”
My guess is we might want to look at graph groups that generate a table with a diagonal whose value is a constant:
1. Let G(V,E) = Peer Group of functions = f1, f2, f3,……f(n-1)
2. All shortest distance matrix: fa(fa) = 0, where a = any integer.
3. Simplest reduction matrix: fa(fa) = 1, where a = any integer.
For example, a clique of five.
Shortest distance matrix:
01111
10111
11011
11101
11110
Simplest reduction matrix:
12222
21222
22122
22212
22221
If at first you don’t succeed, take a break and think about it some more.
Let’s keep things simple:
Peer Group of graph functions = (v1, v2, v3, ……. vn), where each element is a numbered vertex.
If you Google “magma(algebra)- Wikipedia”, you get a nice table that gives you an overview of groups and group like structures.
I have couple of questions.
Are relations (absolute relations) uniquely define group?
Can anyone deduce minimal relations based on multiplication table (reduce it) ? … based on subgroups structure? How hard is to compare 2 relations?
Those are basic questions related to the problem (accessible for wide audience to explore), and I suppose the answers should be known.
Black box permutation group automorphism testing has a lower bound of checking all disjoint prime cycle decompositions. http://oeis.org/A186202
I would formulate the problem as follows: Given a list of permutations on N elements that generates A, and a list of permutations on N elements that generates B, what is the algorithmic complexity to determine if the group A is isomorphic to B under relabeling of the N elements?
Good paper from SODA11, Code Equivalence and Group Isomorphism
http://www.siam.org/proceedings/soda/2011/SODA11_106_babail.pdf
Chad, the problem you formulated is known as “permutational isomorphism of permutation groups.” In a follow-up to the paper you mentioned, Babai, Codenotti, and Qiao show that this problem can be solved in time polynomial in 2^N and the order of the groups. This significantly improves on the naive N! algorithm, enough that they can then use it to show that isomorphism of groups with no abelian normal subgroups can be determined in polynomial time. Their paper hasn’t quite appeared yet, but their results are in Paolo Codenotti’s thesis (http://www.ima.umn.edu/~paolo/thesis.pdf), and it looks like some will be presented at the Joint Math Meetings in January.
That’s very interesting. Is there a naive explanation for why Abelian normal subgroups should make things difficult? I’m still interested in trying to understand what a pair of
-groups that “look the same” but are in fact different might conceivably be like, and I suppose that in principle this result should be providing an important clue.
@gowers: in the case I’m describing below (when you can get two nonisomorphic groups with same profiles of 2-generated subgroups) the reason is that the abelian normal group is in fact central, and most of its elements can be only written as huge products of commutators of many elements. It’s intuitevely clear that if you take two such elements then quotienting anyof them out will lead to the same structure of groups which are generated by small number of elements.
I’ll be interested to see your results about this — and even more so the promised simple explanation. Although it’s not absolutely ideal, what about simply writing it in LaTeX, posting a pdf somewhere, and linking to the pdf from a comment here?
Or perhaps it’s time for someone to set up a polymath wiki. It’s not quite clear to me whether there is a serious intention for this interesting discussion to develop into a sustained attack on the problem. Or perhaps this discussion-plus-private-work is a different style of polymathematical activity that would be worth experimenting with.
As to existence of groups with same subgroup profiles – we have figured out yesterday that it’s even easier than we thought – no need for latex, as it’s just a counting argument. There’s a universal group of Phi-class 2 on n generators (see the paper by Higman) and not less than n generators. Call it E_n. Any other group of Phi-class 2 on n generators is an image of it. It follows that for given n there are finitely many (iso-classes of ) groups of Phi-class 2 generated by n elements. Call the number l(k). Now, Higman constructed roughly p^{n^3} groups of phi-class 2 and order p^n. And in such group there are only (p^n choose k)^l(k) possibilities for profiles of k-generated subgroups, which is a polynomial in p^n.
Explaining how quotients of the universal group E_n are classified is almost done in the Higman’s paper. Basically, the center of E_n is W= V \wedge V, where V is n-dimensional space over F_p. and the quotients are obtained by quotienting out a linear subspace of W. Then isomorphism of the quotients by subspaces A and B lift to isomorphism of E_n which which map A to B. And isomorphisms of E_n which act nontrivially on the center can be shown to correspond to isomoprhism of V, i.e. to GL(V). And it turns out that these automorphism act on W in the obvious way.
Btw, to get groups with the same subgroups profiles one can be much more concrete – it’s possible to quotient out two very concrete 1-dimensional subspaces of W and get different quotients, with same k-profiles.
Problem with polymath for an untenured postdoc like me is my greediness. I read the polymath rules yesterday and as they are written now, there’s no chance of getting a name on the publication. Don’t get me wrong – right now I definitely don’t think there’s anything worth publishing, but I’d like it if there was a possibility. On the other hand, having a dedicated place more friendly than here (latex-wise) to discuss the problem and exchange ideas would be good.
Link to Higman’s paper: plms.oxfordjournals.org/content/s3-10/1/24.full.pdf the relvevant part is Theorem 2.1 and its proof.
The Schreier–Sims algorithm is the most widely used algorithm/data structure for handling basic queries.
http://en.wikipedia.org/wiki/Schreier%E2%80%93Sims_algorithm
My protocol for gathering data would be to generate 100 MB worth of non-isomorphic Cayley tables, and cache their corresponding Schreier–Sims data structures. After that there are a few things you could try… To keep things simple I would start out deriving the optimal algorithm for isomorphism testing of inversion permutation groups (those having only disjoint 2-cycles as generators), then go after groups with both disjoint 2 and 3 cycles.
Conjecture (If false a counterexample would be interesting): Given all pairs of primes i and j; if for all subgroups of group A and group B generated by (disjoint) i and j cycles the groups are isomorphic, then A and B are isomorphic.
I’ve been talking with Nik Nikolov about this problem, and the main outcome is that we can contruct groups with the same profiles of 2-generated subggroups (and probably also of k-generated subgroups, details to be checked). The idea is to study p-groups of Phi-class 2. These are the groups which Higman used to show that “most” p-groups are of class 2. They fit into an exact sequence A -> G ->B where A is the center, and both A and B are vector spaces over F_p.
Their classification problem can be reduced to the following problem. Given a k-dimensional vector space over F_p, form the wedge product W := V \wedge V. Input: subspaces A and B of W, given by their bases. Question: Are A and B in the same orbit of the action of GL(V) on W? Trivial algorithm takes roughly p^{n^2} steps (this is roughly how many invertible matrices there are). Having polynomial time for the group iso problem corresponds to having an algorithm for this problem which runs in poly(p^n) steps.
Both facts are not at all difficult, but I’d prefer to explain them somewhere I can use latex – maybe the polymath project? As to the need for a group theorist for this project, Nik Nikolov is with no doubt a strong group theorist, but I’m not sure he’d be really interested in it. Having said that, I’d probably convince him to have a look every now and then at the polymath project webpage :-).
This was supposed to be a stand-alone comment, not a reply. Sorry for the confusion.
This recent paper by Fabian Wagner http://www.uni-ulm.de/fileadmin/website_uni_ulm/iui.inst.190/Mitarbeiter/wagner/GroupIso_030711.pdf seems to do better than Tarjan’s algorithm. The algorithm rus in O(n^((c log n)/log log n)) some constant c.
He also seems to prove that for any fixed p, there’s a polynomial time algorithm for group isomorphism of p-groups.
Thanks for posting that link. It’s important to note that the paper you linked is incorrect as discussed here in the updated version: http://eccc.hpi-web.de/report/2011/052/
The revised version still seems to have a flaw but the result of p-group composition series isomorphism is still correct.
I also have a new paper (http://arxiv.org/abs/1205.0642) which builds on Wagner’s work to show a deterministic n^{(1 / 2) \log_p n + O(\log n / \log \log n)} algorithm for nilpotent-group isomorphism where p is the smallest prime dividing the order of the group. The 1 / 2 can be replaced with 1 / 4 using randomized algorithms and 1 / 6 using quantum algorithms.