Interdisciplinary Research—Challenges
Issues in doing research across areas
Norbert Wiener was an American mathematician who spent almost all his career at MIT. He is famous for being a child prodigy—when he was young; he is famous for being eccentric—his whole life. There are countless “Wiener” stories. And he is famous for deep results in many aspects of mathematics as well as work in applied areas.
Today I would like to talk about the claim that the best research is interdisciplinary research (IR).
For an example of pure theory, Wiener’s proof of the prime number theorem via analysis is one of the shorter proofs—but relies on a powerful Tauberian result of his. For example of IR, he created the area of cybernetics, which fell out of favor, but is back again—at least the word “cyber” is in vogue.
Wiener often worked on problems that were motivated by applied ideas. He would certainly be called one of the greats in this style of research. Edward Block, the Managing Director Emeritus, SIAM, ended a retrospective he wrote in 2005 by quoting from a front-matter statement in a 1964 volume of Wiener’s papers that is attributed to SIAM:
Professor Norbert Wiener (1894—1964) believed that significant research topics are to be found in the ‘crack’ between two fields. Motivated in this way, he spent much of his life in areas bordering on electrical engineering, physics, and biophysics. His exceptional intuition and profound understanding of mathematics exhibited to him a unity where previously only diversity had been in evidence.
Let’s start talking about IR, but first a story.
A Story
A not too short personal story. Years ago I was the director of graduate studies for the Department of Computer Science at Princeton. One of my jobs was to help manage the PhD. exam. It consisted of three written parts: one on theory, one on systems, and one on applications. During exam week, each candidate student took all three exams. These exams had been made up by each area group and were graded by them independently.
However, the final pass/fail decision was decided by the whole faculty on the Friday of that week. All the faculty meet for the big decision meeting, which was not just a simple adding up the scores. Faculty had input, and some students who did poorly might still pass if they had a champion. It sounds a bit unfair, but it really was a pretty good system. Since we had the raw scores as well as the additional information from faculty members, the results were pretty reasonable.
I would stand in front with the details on slides of how each student did on each exam, and we would discuss each case. Some years it went fast, most years there was some issues. But one year the faculty were quite upset. Here is what had happened:
- There was a system question, I will call S, that all the system students got right. But all the theory students got zero on it.
- There was a theory question, I will call T, that all the theory students got right. But all the system students got zero on it.
This enraged everyone. There were claims from theory faculty that S was an unfair question, and dually there were the symmetric claims from the system faculty that T was unfair. We began to debate this…
Then I looked at the actual questions S and T, and pointed out a curious property: the questions were really the same. They had the same answer. The only difference was the language that was used. Everyone was taken aback. The system question asked for a method to mark a data structure—garbage collection was the expected answer. The theory question basically asked for a method to search a graph—breadth-first search was the expected answer.
I recall two things. The result was that the students all passed. And we had a lengthy discussion on what was wrong with our teaching if the simple change in language threw the students off so badly. We reached no conclusion, although I made a suggestion that was never implemented.
I suggested that we mix all three days’ questions and divide them into three exams: exam I, II, and III. The students would be given the exams on successive days. Since the questions were mixed together randomly, they would not know which questions were systems or theory or applications. I thought this might be pretty good, and so did almost two thirds of the faculty. But the other two thirds of the faculty hated the idea and so nothing happened. Yes,
sometimes—especially when one counts faculty opinions.
Problems
The fundamental issue that I came to realize was this simple insight: Problems do not come with labels. Students should not expect that they will be told in the future that this problem is a theory one, and that is a system one, and so on. They should know that problems in real life come without labels—there may be no simple marker that suggests what type a problem is.
Language
Each field has its own language which acts a barrier for IR. In the exam case the simple switch from asking about graphs to asking about linked data items threw our students. One of the issues that we face in IR is the lack of agreement on what is meant by simple words or phrases. This is obvious, but still a barrier that can be difficult to overcome.
World View
Perhaps more vexing is the views that each area takes. Let’s look at the simple assertion that 
But physics is full of equations that hold approximately and that is just fine.
This is a famous rule that helped unravel the original structure of DNA and led to the breakthrough of James Watson and Francis Crick. But it is not always true. I worked years ago with biologists and discovered that it was more a guideline than a rule. In nature sometimes wrong pairs did pair up.
Here 
Not only are there variants on this equation—which is really an approximate model—one can find numerous personifications of these variants. One paper asked, “Does the St. Louis Equation Now Believe in Fiscal Policy?” while another presented “Democratic” and “Republican” versions. The same course began with the equation
where for time period 
Cybernetics in Full
Cybernetics can be treated narrowly as meaning control systems for electronic equipment. The original vision and proper meaning is broader and more foundational. Wiener’s 1954 book Cybernetics was subtitled, “the control and communication in the animal and the machine.” In it he stated:
the purpose of Cybernetics [is] to develop a language and techniques that will enable us indeed to attack the problem of control and communication in general, [and] also to find the proper repertory of ideas and techniques to classify their particular manifestations under certain concepts.
Besides putting the emphasis on language, this made the problem one of studying how an animal or machine becomes familiar with its environment and influences it. The advent of the Internet as an organism for research is causing us to re-evaluate the kind of communication and familiarity needed.
Wiener even probed the issue of background and environment in regard to empirical science:
What most experimenters take for granted before they begin their experiments is infinitely more interesting than any results to which their experiments lead.
What assumptions are we making when we formulate problems for a research agenda, and what if they are orthogonal to those of a prospective partner in another discipline? What aspects of communication might fall through the crack and make it hard to find the common research topics inside the crack?
Open Problems
The question is simple: how can we carry out IR with these roadblocks? What is the best way to overcome them?
[fixed formatting of Block quote and crack photo.]
Norbert Weiner’s 1959 novel The Tempter can be read as an extended meditation on the topic of interdisciplinary research and systems-level control, both narrowly at the machine level and broadly at the societal level. And I will venture the opinion, that it is necessary to read Weiner’s novel this way, because the characterization in Weiner’s novel is more nearly
-dimensional, than 
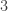-dimensional. In short, when it came to novelistic talent, Norbert Weiner wasn’t JK Rowling! 🙂
A recent review by Philip Davis in SIAM News (2005) sums up Weiner’s novel this way:
It seems to me that nowadays Weiner’s novel can be read more sympathetically and deeply than that. The colliding themes of human values, intellectual property, and global-scale enterprise — which are the dominant themes of Weiner’s 1959 novel — nowadays are shaping the world’s research community even more dominantly than in Weiner’s era.
So one way to parse Dick’s question: “How can we carry out [interdisciplinary research] with these roadblocks?” is to take a tip from Norbert Weiner’s novel — and also from von Neumann;’s similarly-themed essay The Mathematician (1947) — and appreciate these seeming roadblocks as Nature’s way of encouraging us to perceive new opportunities and create new global-scale enterprises … without any warranty that these new opportunities will be easy to recognize, or that their associated enterprises will risk-free, or that human motivations will be entirely saintly, or that the associated processes of human cognition will be entirely rational.
Interesting freudian slip: once out of ten times you say Wiener instead of Weiner
LOL … Bourbaki, it was Freud who observed “Sometimes a cigar is just a cigar.” Nowadays both Google’s Ngram Viewer and the Arxiv fulltext search engine can show us instantly the prevalence of Weiner
Wiener transliteration … the prevalence turns out to be a startlingly high 6-8%. 😉
I will now happily quote Lipton as saying the best research is IR. 🙂
Prof. Lipton,
Beautiful post as always. As an aside, I would like to share some lines from “Cybernetics” (by Wiener) that I really find relevant to the general theme of the post.
R.S.McNamara
It’s interesting that while cybernetics started out as an interdisciplinary field, and a proposed theory of (almost) everything, it survives in the form of control theory and information theory (the latter might be controversial… what did Shannon think about cybernetics as a field)? When interdisciplinary research is successful, it becomes “normalized” and stabilized in the form of new disciplines. Molecular biology is another example.
One of the biggest challenges in working at the boundary between disciplines is that it’s easy to be a dilettante — to impress people from field A with your knowledge of field B and vice versa, without doing deep work in either one. Moreover, there are sometimes strong incentives for precisely this kind of behavior.
Doing interdisciplinary research in a principled way often means a low publication rate for several years as you learn the techniques and terminology of the new field. I was lucky enough to meet some great collaborators who helped me through this process, and I was lucky enough to be employed by institutions that supported me along the way. But it took time, and there were points in my career where my future was genuinely uncertain.
We need hiring, tenure, and promotion policies that truly support interdisciplinarity, as opposed to giving it lip service.
In a simplistic sense, at the bottom of everything is a vast number of epiphenomenon that behave via constrained relationships. But as we work our way upwards, each different discipline has a tendency to ascribe very different terminology and symbolism in their explanations. The commonalities get overlooked as specialization increases.
I’ve always suspected that increases in the digital representation of our knowledge bases would allow for a significant increase in mining these structurally similar pieces. Once the terms and history get stripped away, all that remains are structural maps of high-level interactions. If we collect and categorize enough of these, we’ll be able to leverage them to increase our understanding. We’ll also get a deeper insight into what we don’t know.
At our present accelerated pace, it should be any century now …
Paul.
Paul, your post shares themes that are discussed (at considerable length) in a remarkable letter to Norbert Wiener from John von Neumann (1946) … a letter that anticipates (in greater depth, and more than a decade earlier) the major themes of Richard Feynman’s relatively better-known essay There’s Plenty of Room at the Bottom (1959).
One major difference between the 20th century and the 21st century — as it seems to me — is simply this: in our 21st century the 20th century dreams of Wiener, von Neumann and Feynman are coming true … rapidly.
Thanks for the link John, that was really interesting reading. I’m not deeply familiar with biology, has von Neumann’s underlying description of the complexity of a virus remained accurate? I felt he might be underestimating the complexity? His sense of “massive fast computing” has certainly changed 🙂
I’m always amazed at how quickly our collective knowledge has increased in such a short time. And yet fascinated by how much is still left to understand …
Paul.
Paul, the short answer is that von Neumann / Wiener / Feynman were reasonably accurate in their assessment of the complexity of living organisms, and in particular, von Neumann was prescient to foresee (in 1946!) that heredity would rest upon pairwise combinatoric chemistry (the G
C and A
T of the genetic code).
And yet von Neumann / Wiener / Feynman, and their whole generation of scientists, all wrongly failed to foresee that radiation damage would prove intractable for atomic-resolution biological electron microscopy, and perhaps for this reason they also failed to appreciate the broad practical applicability of long-wavelength (hence nondestructive) magnetic resonance imaging methods.
In retrospect, we now appreciate there was no practical obstruction in math-or-physics to inventing (for example) magnetic resonance imaging as early as the 1930s or 1940s, instead of the 1980s.
Thus history shows us that even top-rank geniuses sometimes overlook simple ideas … which is encouraging! 🙂
Opps. Bacteria, not virus. I think the later is simpler?
Dear Prof. Lipton, I found this article particular interesting because it puts Norbert Wiener in the right light half a century after his death.
Having read 25 years ago the famous Steve Heims biography “Norbert Wiener and John von Neumann” I was always convinced that Wiener was an important scientist. Unfortunately I came at one of my last London stays across a very contemptuous historian of science who just considered Wiener as a very average scientist whose contribution to progress could be subsumed by having computed artillery firing tables during WW2.
Would I still remember this historian’s name ( what I don’t ) I’d sent him
a reference of your IR article.
Indeed we wanted to convey Wiener’s intellectual heft by saying more about his Tauberian theorem—and its possible use to approximating exponential-sized sums that we are looking at. But it would have given the post too much heft, and Dick has been traveling while I’ve had a lot of Internet engagement following the unveiling of my chess research—which I’ve also made an advance on this past weekend while I’m supposed to be doing other things for this blog…
Bourbaki, in addition to seconding your recommendation of Steve Heims’ outstanding Norbert Weiner and John von Neumann, please let me commend also to GLL readers two more recent works:
• Neil Sheehan’s A Fiery Peace in a Cold War: Bernard Schriever and the Ultimate Weapon (2009):
• Stephen B. Johnson’s The Secret of Apollo: Systems Management in American and European Space Programs (2002):
In summary:
Thus, whenever we look for lessons-learned from technological roadmaps — the QIST Roadmaps are a good example — we can facilitate that analysis by reflecting upon “Engine Charlie’s” maxim.
These works provide us with a short (perhaps too short?) and simple (perhaps too simple?) answer to Dick’s GLL question: “How can we carry out IR with these roadblocks? What is the best way to overcome them?”
“Engine Charlie” provides the short simple answer: “Start making trouble.” 🙂
@mr. Slides
you really have a pronounciation problems with Norbert Wiener. Me like good old Siegmund would rather point to another paradigm than the cigar symbolic. 😉
I think it was Herbert Simon who first mentioned the importance of representation in problem solving. It is not simply a matter of language or labeling, the problem you mention was stated using two different representations, each representation making the problem more accessible in a different knowledge domain.
The “Story” is interesting, but I don’t think it’s surprising, and I’m of the opinion that it really can’t be resolved. I deal with it all the time (albeit at a pre-algebra, etc., level). As I’ve been convinced by cognitive science in the past few years, comprehension is always very domain-specific, and subject to how familiar one is with those examples (per various articles in American Educator magazine). I think it’s a bit of a common mistake by some math professionals to think that because a student can solve problem A, analogous problem B which is the same in the abstract, can also be automatically solved (and I’ve been dealing with some really atrocious textbooks that make that mistake, and never give students a proper chance to practice in a particular domain to achieve fluency).
Obviously I can understand statement S1 in English, and yet have no chance of even identifying the equivalent statement S2 in some other language. The only solution is to spend time acquiring that other language-set. And I think that the problem-solvers and researchers who can see the connections and commonalities to make advances in the abstract like this are simply a very special breed (and are dependent on having a unique breadth of knowledge).
I wonder which definition of equality the author used when saying garbage collection = breadth-first search.