Quantum Refutations and Reproofs
One of Gil Kalai’s conjectures refuted but refurbished
Niels Henrik Abel is famous for proving the impossibility of solving the quintic equation by radicals, in 1823. Finding roots of polynomials had occupied mathematicians for centuries, but unsolvability had scant effort and few tools until the late 1700’s. Abel developed tools of algebra, supplied a step overlooked by Paolo Ruffini (whose voluminous work he did not know), and focused his proof into a mere six journal pages.
Today our guest poster Gil Kalai leads us in congratulating Endre Szemerédi, who on May 22 will officially receive the 2012 prize named for Abel. He then revisits his “Conjecture C” from his first post in this series, in response to a draft paper by our other guest poster Aram Harrow with Steve Flammia.
Szemerédi’s prize is great news for Discrete Mathematics and Theoretical Computer Science, areas for which he is best known, and this blog has featured his terrific work here and here. The award rivals the Nobel Peace Prize in funds and brings the same handshake from the King of Norway.
Gil offers the analogy that Abel’s theorem showed why a particular old technology, namely solution by radicals, could not scale upward beyond the case of degree 4. The group-theoretic technology that superseded it, particularly as formulated by Évariste Galois, changed the face of mathematics. Indeed Abelian groups are at the heart of Peter Shor’s quantum algorithm. Not only did the work by Abel and Galois pre-date the proofs against trisecting angles, duplicating cubes, and squaring circles, it made them possible.
Refutations and Revisions
Gil’s analogy is not perfect, because quantum computing is hardly an “old” technology, and because currently there is no compelling new positive theory to supersede it. Working toward such a theory is difficult, and there are places where it might be tilting against the power stations of quantum mechanics itself. In this regard, Aram and Steve’s paper provides a concrete counter-example to a logical extension of Gil’s conjecture for the larger quantum theory, in a way that casts doubt on the original.
The refutation and revision of conjectures is a big part of the process described by Imre Lakatos in his book Proofs and Refutations, which was previously discussed in this blog. Here, the conjectures are physics conjectures, related to technological capability, and the “proof” and “reproof” process refers to confronting formal mathematical models with (counter-)examples and various checks by observations of Nature.
After two sections by Aram and Steve explaining their paper and its significance, Gil assesses the effect on his original Conjecture C and re-assesses its motivation. The latter is reinforced by a line of research begun in 1980 with the following question by Sir Anthony Leggett, who won the Nobel Prize in Physics in 2003:
How far do experiments on the so called “macroscopic quantum systems” such as superfluids and superconductors test the hypothesis that the linear Schrödinger equation may be extrapolated to arbitrary complex systems?
Leggett’s “disconnectivity measure” in his 1980 paper, “Macroscopic Quantum Systems and the Quantum Theory of Measurement,” was an early attempt to define rigorously a parameter that distinguishes complicated quantum states.
In this light, Gil formulates two revisions of his conjecture that stay true to his original intents while avoiding the refutation. Then I (Ken) review lively comments that continue to further the debate in previous posts in our series.
Aram Harrow, with Steve Flammia
Recall that Gil defined an entanglement measure 
There is a fixed constant
, possibly
, such that for states
produced by feasible
-qubit quantum computers,
Here the technical meaning of “feasible” depends on which models of noisy quantum computers reflect the true state and capability of technology, and is hard for both sides to pin down. We can, however, still refute the conjecture by finding states
Our point of attack is that there is nothing in the definition of 
Call that Conjecture C’. As Gil agrees, our note shows unconditionally that Conjecture C’ is false, for any 
Theorem 1 There exist intuitively feasible
.
It is important to note that with 
What the Conjecture is Driving At
Conjectures of this kind, as Steve and I see it, are attempts at what Scott Aaronson calls a “Sure/Shor separator.” By his definition that would distinguish states we’ve definitely already seen how to produce from the sort of states one would require in any quantum computer achieving an exponential speedup over (believed) classical methods. It represents an admirable attempt to formulate QC skepticism in a rigorous and testable way.
However, we believe that our counterexamples are significant not especially because they refute Conjecture C, but because they do so while side-stepping Gil’s main points about quantum error correction failing. More generally, we think that it’s telling that it’s so hard to come up with a sensible version of Conjecture C. In our view, this is because quantum computers harness phenomena, such as entanglement and interference, that are already ubiquitous. Nature makes them relatively hard to control, but it is also hard to focus sensibly on what about the control itself is difficult. The formulations of Conjecture C and related obstacles instead find themselves asserting the difficulty of creating rather than controlling. Of course they are trying to get at the difficulty of creating the kinds of states needed for controlling, but the formulations still wind up trying to block the creation of phenomena that “just come naturally.”
In our view, the situation is similar to ones in classical computing. A modern data center exists in a state of matter radically unlike anything ever seen in pre-industrial times. But if you have to quantify this with a crude observable, then it’s hard to come up with anything that wasn’t already seen in much simpler technology, like light bulbs. Our note can be thought of as showing that Conjecture C refers to a correlation measure that is high not only for full-scale quantum computers, but even for the quantum equivalent of light bulbs—technology that is non-trivial, but by no means complex.
(source)
Gil Again: Revising Conjecture C
One of the difficult aspects of my project is to supply mathematical engines for the conjectures, which were initially expressed in informal English terms and with physical intuition. For example, in Conjecture 4 we need to define “highly entangled qubits” and “error-synchronization” formally. This crucial technical part of the project, which is the most time-consuming, witnessed much backtracking. It happened with initial formulations for Conjecture 4 that failed when extended from qubits to qudits, which was indeed a reason for me to dismiss them and look for a more robust one, and this has guided me with other conjectures.
Aram and Steve’s example suffices to look for another formal way to express the idea behind Conjecture C. While rooted in quantum computer skepticism, Conjecture C expresses a common aim to find a dividing line between physical quantum states in the the pre- and post-universal quantum computers eras. When Aram’s grandchildren will ask him, “Grandpa, how was the world before quantum computers?” he could reply: “I hardly remember, but thanks to Gil we had some conjectures regarding the old days”—and the grandchildren will burst in laughter about the old days of difficult entanglements.
Conjecture C expresses the idea that “complicated pure states” cannot be approached by noisy quantum computers. More specifically, the conjecture asserts that quantum states that can be realistically created by quantum computers are “
We can be guided by the motivation stated on the first page of the paper by Anthony Leggett mentioned above, for his “disconnectivity measure” which intends to distinguish two kinds of quantum states:
Familiar “macroscopic quantum phenomena” such as flux quantization and the Josephson effect [correspond to states having very low] disconnectivity, while the states important to a discussion of the quantum theory of measurement have a very high value of this property.
Leggett has stayed active with this line of work in the past decade, and it may be informative to develop further the relation to his problems of quantum measurement and problems in quantum computation. In this general regard, let me discuss possible new mathematical engines for the censorship conjecture.
Conjecture C For Codes
Error-correcting codes are wonderful mathematical objects, and thinking about codes, is always great. Quantum error-correcting codes will either play a prominent role in building universal quantum computers or in explaining why universal quantum computers cannot be built, whichever comes first. The map I try to draw is especially clear for codes:
Conjecture C for codes: For some (small) constant
Like in the original version of Conjecture C our notion of approximation is based on qubit errors. Conjecture 1 in the original post asserts that for every quantum error-correcting code we can only achieve a cloud of states, rather than essentially a Dirac delta function, even if we use many qubits for encoding. The expected qubit errors of the noisy state compared to the intended state can still be a small constant. Conjecture C for codes asserts that when the code corrects many errors than this cloud will not even concentrate near a single code word. Here “many” may well be three or even two.
Conjecture D for Depth
Conjecture C for codes deals only with special types of quantum states. What can describe general pure states that cannot be approximated?
Conjecture D: For some (small) constant
, pure states on
Here we adopt the ordinary description of quantum circuits where in each round some gates on disjoint sets of one or two qubits are performed. Unlike the old Conjecture C which did not exclude cluster states, and thus could not serve as a Sure/Shor separator in Scott Aaronson’s strict sense, the new Conjecture D may well represent such a separator in the strict sense that it does not allow efficient factoring. It deviates from the direction of earlier versions of Conjecture C since it is based on computational theoretic terms.
The new Conjecture D gives a poetic justice to bounded depth circuits. In classical computation, bounded-depth circuits of polynomial size give a mathematically fascinating yet pathetically weak computational class. In quantum computation this may be a viable borderline between reality and dream.
In the Comments
The comments section of the “Quantum Super-PAC” post has seen an extremely lively discussion, for which we profusely thank all those taking part. We regret that currently we can give only the barest enumeration of some highlights—we envision a later summary of what has been learned.
Discussion of a possible refutation of Gil’s conjectures via 2-local properties started in earnest with this comment by Joe Fitzsimons. See Gil’s replies here and here, and further exchanges beginning next.
John Sidles outlined a mathematical approach to the conjectures beginning here. Hal Swyers moved to clarify the physics involved in the discussions. Then John Preskill reviewed the goings-on, including 2-locality and the subject of Lindblad evolution as used by Gil and discussed extensively above, and continued here to head a new thread. Swyers picked up on questions about the size of controllable systems here and in a second part here. Gil outlined a reply recently here.
Meanwhile, Gil rejoined a previous post’s discussion of the rate of error with a comment in the “Super-PAC” post here. Alexander Vlasov re-opened the question of whether the conjectures don’t already violate linearity. Sidles raised a concrete example related to earlier comments by Mikhail Katkov here. Then Gil related offline discussions with David Deutsch here.
Gil has recently reviewed the debate on his own blog. He and Jim Blair also mentioned some new papers and articles beginning here. On the technological side, Steve Flammia noted on the Quantum Pontiff blog that ion-trap technology has taken a big leap upward in scale for processes that seem hard to simulate classically, though the processes would need to be controlled more to support universal quantum computation.
Open Problems
Propose a version for Conjecture C or D, or explain why such a conjecture is misguided to start with.
Trackbacks
- Sometimes They Come Back | Are You Shura?
- The Quantum Fault-Tolerance Debate Updates | Combinatorics and more
- RT.COM -> Это происходит, на каком языке? -> WHAT R U –PEOPLES DOING?זה קורה ב איזה שפה?זה קורה באיזה שפה?זה קורה באיזה שפה?זה קורה באיזה שפה– BIBI ?Dit geb
- Can You Hear the Shape of a Quantum Computer? « Gödel’s Lost Letter and P=NP
- Giants Known For Small Things « Gödel’s Lost Letter and P=NP
- Quantum Repetition « Gödel’s Lost Letter and P=NP
- Lucky 13 paper dance! | The Quantum Pontiff
- Quantum Supremacy or Classical Control? « Gödel’s Lost Letter and P=NP
- The Quantum Debate is Over! (and other Updates) | Combinatorics and more
- My Quantum Debate with Aram III | Combinatorics and more
- Happy 100th Birthday, Paul Erdős | Gödel's Lost Letter and P=NP
I wish some computer scientist would write about Alexander Grothendieck.
Do I feel my leg being gently pulled? 🙂
Ah yes, what a genius! I agree he’d have done marvels in computer science, even though his revolutionary achievements in algebra, geometry, topology, categories, philosophy, let alone his political involvements, are well enough for one lifetime. 🙂
Serge, a newly published book well-worth reading is Elaine Riehm’s and Frances Hoffman’s Turbulent times in mathematics: the life of J. C. Fields and the history of the Fields medal (2012) in which we find the following quotation from David Hilbert, who at the 1928 ICM endeavored to restore the bonds of mathematical collegiality that had been shattered by the First World War:
The sobering failure of Hilbert’s 1948 efforts was to become evident evident in the sad circumstances of Hilbert’s own death, and the desperate circumstances of Grothendieck’s own childhood, in the heart of the Third Reich.
Are present-day circumstances any less sobering, than those of Hilbert’s era, and of Grothendieck’s era? Is the role of mathematics any less central? Appreciation and thanks are due to Elaine Riehm and Frances Hoffman, for writing a book that helps us to ponder these questions.
We have a scheme to talk about Grothendieck sometime in the summer.
Hoorah! Ken, that’s exciting to look forward to! Serge’s post was correct (IMHO) the successes and failures of Grothendieck’s wonderful enterprises are confounding, delightful, disturbing, and instructive for all STEM disciplines.
🙂
yay…
Quantum space is defined as the extra space when the integration of the matrix P=1 gets off the boundaries. as in P=1 square . the inverse functions on radicals have to comply with the equivalence. not as an Arch function were the real numbers change value on the negative sector. positive negative positive as logic gates for a nano circuit, are god for a logic circuit in a binary system. on the hyperbolic functions c=2 has an exponential on real numbers and a radical in prime numbers. this problem gave to Enrrico Fermi the ability to create a fermion. and Einstein created the solution using 1/2 of the sine 1/2 cosine to create a prime number that can have a solution as a radical and exponential.so the quantum space could exist without problem. P=NP eliminating the bipolarity on the second factor. when reaches a speeds faster than the speed of light. the particle accelerator does not reach speeds faster than the light. using C=2 if C is the constant of the speed of light as seen in the equation of Apple computers robot Jeffrey 5000 creates a gravitational force. but does not reach the prime interface as described by Einstein were Gravity creates the inverse Matrix of p=1. is different than the Arch Matrix of P=1.
This is a physics problem, and making conjectures with no basis in physics does not make sense. Are you really suggesting that Nature sees that you are trying to prepare a state encoded in a quantum error-correcting code and decides to stop you?
I strongly disagree with calling these random, unsupported guesses “conjectures.” A conjecture should have at least some reason behind it, not just “gives poetic justice to bounded-depth circuits.”
Hi Rachel
Good question! It is a natural question to ask if in nature we can witness approximately pure states manifesting long (or high-depth) quantum processes. (Let us even allow unlimited computation power to control the process.) After all, unless there is some fault-tolerant machinary it is hard to see how “long” quantum process can stay approximately pure. So bounded-depth processes is a natural proposal for the limit of quantum processes that do not manifest quantum fault-tolerance.
The impossibility of deciding whether P=NP is a direct consequence of Heisenberg’s uncertainty principle.
why?
why would anyone even study such a possibility? It is like saying I cannot count n! quickly because of Cauchy-Schwarz!
why would anyone even study such a possibility? It is like saying to know whether I cannot count n! quickly because of Cauchy-Schwarz is undecidable!
Not exactly. With P=NP you have a speed” – that of computer processes – and a “position” – the accuracy of the output result. I believe that the product of the probability for an algorithm to output accurate results by the probability for it to be efficient is lower than some fixed constant. I claim that both phenomenons – the one about quantum particles and the one about computer processes – are implied by some more general principle, though I can’t write out the details of a relationship between my principle and Heisenberg’s.
Couchy effect as an absorption coefficient can be used on different conditions, but specially under a gravitational force. as the Schwarzchild equation measures the compression state of the space under gravity force. Here is when Einstein observes that light behaves as matter and is affected by gravity also.calculates the strength of the inertial force produced by the black holes. as a P=NP its assumed that NP can coexist in the same time space, and this condition presumes the existence of a great gravitational force, in the form of antimatter . here N would be the Anti-quark, or anti-proton and P the real number(X), that exists inside the schwarz ring of gravity. Couchy measures the intensity and speed of the absorption. However to consider that the quantum space does exist without that intense gravity would be uncertain as trying to decide the sex of a baby. here a radical have to be a proportional exponential to the times square. means we have to compress two dimensions, one for N and one for P.when C=Constant of the speed of Light and you take C=2 you create this uncertainty dilemma. its only when you consider C=Csquare when the time space paradox allows you N for Quantum space and a real space for P=1. see Schrodingers cat paradox. The Linear space with Reimman and Euler.The integration of two dimensions that allows you the existence of antimatter is still under test in the Linear particle accelerator that has fail to prove the existence of antimatter in the Higgs Boson concept The Tevatron cannot go faster than the speed of Light.
🙁
On Shtetl Optimized, in response to a well-posed question from Ajit R. Jadhav, I described a toolkit for quantum dynamical simulation in which Conjecture C holds true, and yet the framework is sufficiently accurate for many (all?) practical quantum simulation purposes. A bibliography is included. The aggregate toolkit contains perhaps not even one original idea … still it is fun, and useful too, to appreciate how naturally many existing dynamical ideas mesh together.
As for whether Nature simulates herself via this toolkit, who knows? The post does sketch an alternative-universe version of the Feynman Lectures that encompasses this eventuality.
Dear all, Greetings from Lund.
I am here for the Crafoord days celebrating the Crafoord Prize being given to Jean Bourgain and Terry Tao. There is a symposium entitled “from chaos to harmony” celebrating the occasion http://www.kva.se/sv/Kalendariumlista/Event/?eventId=386 with live video of the five lectures here http://kvatv.se/ .
Here are some questions I am curious about regarding the topic of the post:
1) Can somebody explain Leggett’s parameter precisely? I remember that when I tried to understand it (naively perhaps) the parameter was large for certaib systems with large classical correlations. In any case, I would be happy to see a clear explanation what the parameter is.
2) What could be potential counterexamples to the suggestion that all natural (approximately) pure evolutions are of (uniformly) bounded depth.
3) Is the note by Aram and Steve gives a convincing evidence regarding Conjecture C in its original form. I am very thankful to Aram and Steve and overall I was quite convinced. But I am not entirely sure.
This has two parts:
a) Is the state W realistic?
b) Is Conjecture C’ in the form refuted by them (and there is no dispute that their example refute Conjecture C’) the right extension to qudit-operated QC of the qubit version.
To add to 1), consider a quantum circuit that maps the all-|0> state to a state f. Is there an easy way—preferably gate-by-gate inductive—to compute Leggett’s D-measure of f?
I would find it hard to think of a reason why it wouldn’t be. It’s essentially what you get when a single photon is absorbed by a gas cloud, or when you put a single photon through a defraction grating.
Joe, you probably know this stuff better than me, but for a gas cloud of N atoms, doesn’t the temperature have to scale like 1/log(N)?
For photons that’s also true, but I think with a better prefactor. For example, modes of an X-ray probably have very little thermal noise in them.
Hi Aram,
I was thinking of things like vapor cell quantum memories, which store the quantum state essentially as a w-state (see http://www.nature.com/nphoton/journal/v3/n12/abs/nphoton.2009.231.html) and have been demonstrated with reasonable fidelities. While certainly these are essentially constant sized devises, the constant is enormous.
Cool, thanks!
The W- state as a receptor, it does absorb wave length frequencies and they are used as synthetic retina for digital cameras, they do absorb light and releases it, the main trick here is that the photon is turned into an electric current as in the solar panel arrays. so in this way the encoded information can be transcribed into zeros and ones.Bose-Einstein condensate obtains the harmonic state of some gases when they are under pressure and a near to absolute Zero K temperature.The solid state receptors for Wide Band Antenna does work on Microwaves capturing and releasing the information that is in the air. however the antenna position losses its grip to the sine of the wave so the new W-state receptors have multiple position on fractal arrays to correct this problem, as in your cellular.
For Leggett’s parameter, it’s crucial that the parameter “a” be taken to be <1/2, so that classical systems always have disconnectivity equal to 0. If you take it to be 1/3, then this says that D is the largest N such that for all subsets of N qubits and all divisions of those qubits into subsystems A, B, we have S(AB) <= (S(A) + S(B))/3, where S() is the von Neumann entropy.
For evidence of depth, I think that the presence of iron in the Earth is pretty good evidence. The only natural process we know for creating it is stellar nucleosynthesis, which (a) takes a very long time, and (b) requires quantum mechanics (and (c), I had to look up the name of on wikipedia..). Because of (a) and (b), we have evidence of deep quantum processes. I can't prove this, since I can't rule out the possibility of a low-depth classical method of producing lots of iron. Rather I think the evidence for it is like the evidence for evolution, which is that it's the only plausible theory that is consistent with the data, and that the theory alone has predicted things that weren't originally used to derive the theory.
Note that I didn't say anything about any states being pure. This is because purity is subjective, and I don't know of a way for our physical theories can meaningfully depend on this. This of course is a common theme in my (and Rachel's and Peter's and others) objections to Gil's conjectures, which is that they are phrased in ways that suggest Nature may have to know which states we prefer the system to be in.
Dear Aram, this is a great comment with a lot of interesting things to think about. I am enthusiastic to see this clear explanation of Leggett’s parameter (and it would be nice to discuss this parameter), and the iron as evidence for depth is exciting and we should certainly discuss it.
I suppose I do not understand the point about purity. What do you mean by purity being subjective, what is “this” that physical theory cannot depend on and what is the critique on my conjecture that is referred to.
Hi Aram, here is a remark regarding Leggett’s parameter as you described it. In the context of Conjecture 4 and the notion of “highly entangled state”, one idea was to base the notion on entanglement between partitions of the qubits into two parts. A counterexample for this idea but for qudits that came up in a discussion with Greg Kuperberg some years ago looks like this:
let G be an expanded graph with valence 3 and with 2n vertices.
Take 3n Bell pairs and arrange them into 2n qudits with d=8 according to
the pattern of the graph G. Then at the d=8 qudit level, this state has a lot of excess entanglement for partitions into two parts. This is achieved simply by
grouping the halves of the Bell pairs and not by doing any true quantum
information processing.
So maybe this is an example also of a very mundane state that represents high value of Leggett’s D-parameter.
Regarding the expander counter-example: there’s something a little ambiguous about Leggett’s definition in that he states it for states that are symmetric under permutation, so that the reduced state of any N
particles depends only on N. Probably the right pessimistic
interpretation for non-symmetric states is that you want to choose the
worst subset.
So then it becomes
“D := max N s.t. for any S with |S|=N there exists T\subset S s.t.
H(rho_S) <= delta (H(rho_T) + H(rho_{S-T})) "
But if that's the definition, then D will be very low for this
expander construction you described And for most non-symmetric states
I can think of.
It doesn't feel like a very robust definition, though. If we replace
|S|=N with |S|<=N then you get something different. Presumably also
we should restrict N to be << system size.
And certainly replacing "for any S" with "exists S" would be far too permissive; then just having a bunch of EPR pairs would count.
I am struggling with this too. Hopefully the following LaTeX will be OK (apologies in advance if there are bugs).
An explicit definition of
is given in Leggett’s article (eqs. 3.1-3), and three concrete examples are worked out (the first example is marred by a typographic error: 
should be 
).
The part of the definition that I struggle with is the pullback-and-partition of the entropy
onto subsystems. In particular, the post-pullback partition into (spatially separated? weakly coupled?) subsystems is problematic … and such partitions are problematic in classical thermodynamics too.
Presciently, Leggett’s article authorizes us to adjust the definition of
as needed:
We continue as follows, with a view toward eliminating problematic references to separation. Let a system
be simulated on a Hilbert space 
by unraveling an ensemble of Lindbladian dynamical trajectories, and let 
be the density matrix of the trajectory ensemble thus simulated. Pullback the Lindbladian equations of motion and dynamical forms onto a rank-
tensor product manifold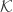 
and let 
be the density matrix of the trajectory ensemble thus simulated. By analogy to the Flammia/Harrow measure 
, define a rank-dependent Kalai-style FT separator measure 
to be a minimum over the choice of tensor bases of the trace-separation
Then a Leggett-style rank-based variant of Kalai Conjecture C is
This conjecture possesses the generic virtue of most tensor-rank conjectures: computational experiments are natural and (relatively) easy. It also has the generic deficiency of tensor-rank conjecture: it is not obvious (to me) how the conjecture might be rigorously proved.
Close … let’s try again … “Then a Leggett-style rank-based variant of Kalai Conjecture C is:”
Apologies for the
glitches! 🙂
Aram and Steve refer in several places to “our note” … it would be helpful if a link were provided to this (otherwise mysterious) note. Or have I just overlooked a link?
“Note” and “paper” are synonymous—the post went thru a long edit cycle, and their April 16 ArXiv upload came in the middle of that. The link is at the top: http://arxiv.org/abs/1204.3404, and actually until three days ago it was at a less-stable “arxaliv” link.
Thank you, Ken, for clarifying that! The Flammia/Harrow note “Counterexamples to Kalai’s Conjecture C” looks exceedingly interesting & employs several novel constructions … plausibly it will require comparably to digest as it took to conceive! 🙂
As I slowly digest Steve and Aram’s (really excellent and enjoyable!) arXiv note “Counterexamples to Kalai’s Conjecture C” (arXiv:1204.3404v1]), one concern that arises is associated to the restriction “states ρ which have been efficiently prepared.”
In designing an apparatus for efficient state preparation, it is natural to begin by generalizing the apparatus shown in Figure 1 (page 6) of Pironio et al’s much-cited “Random Numbers Certified by Bell’s Theorem” (arXiv:0911.3427v3). The natural generalization is conceptually simple: specify more ion cells, that generate more outgoing photons, such that state preparation is heralded by higher-order coincidence detection, as observed through unitary-transform interferometers having larger numbers of input/output channels. Visually speaking, just add more rows to Figure 1!
AFAICT, in the large-n qubit limit this natural generalization is robust with respect to validation (that is, the state heralding is reliable, when we see it) but it is exponentially inefficient (the mean waiting time for state heralding is exponentially long in n).
We might hope that this efficiency obstruction is purely technical, to be overcome (e.g.) with greater detection efficiency and lower-loss optical coupling between ions and detectors. But this limit is of course the limit of strong renormalization, and it is not obvious (to me) that the qubit physics remains intact following strong renormalization. These are hard questions.
Over on Shtetl Optimized, where these same issues are being discussed, I had occasion to quote the following passage:
Among practicing researchers, this comforting belief — which has the great merit of being immensely inspiring to beginning students — was perhaps more widely held in the 20th century than at present … because the immensely long, immensely difficult struggle to build working quantum computers has slowly and patiently been teaching us humility.
That the Kalai/Flammia/Harrow Conjecture C includes the phrase “efficiently prepared” (as contrasted with “efficiently described” for example) is evidence that these lessons-learned are being assimilated and acted-upon. Surely there is a great deal more to be said regarding these issues and obstructions, and we can all hope that one outcome of this debate will be a jointly-written note from Aram and Steve and Gil, that surveys and summarizes (for 21st century students especially) the wonderfully interesting challenges and opportunities that are associated to this fine debate.
Hi John, those are some good points, which I won’t fully address. But I do agree that experiments that wait for multiple coincidences are not scalable, and wouldn’t work for this kind of thought experiment. On the other hand, something like what Boris Blinov’s group is doing (using entangled photons to entangle distant ions) would, I believe, address this problem. Obviously doing such an experiment once isn’t easy, and doing it N times in parallel is only harder, but it’s almost certainly harder only by a linear factor.
Aram, a reference would be very helpful.
I had a professor who was fond of quoting Julian Schwinger to the effect that certain facts were “well known to those who knew them well.”
In a similar vein, the arXiv note refers to “states whose physical plausibility is relatively uncontroversial” … and so it is natural and legitimate to wonder whether this opinion is shared by folks whose job it is to prepare these states.
Some of this work is planned for the future, but this paper describes those future plans.
I think it’s uncontroversial that the states are physically plausible, and that any fundamental obstacle to their creation would be extraordinarily surprising, like discovering new energy levels for the Hydrogen atom. But that is consistent with the fact that doing the experiment once is going to be very hard, and doing it N times will be something like N times as hard.
Aram, I will look carefully at the link you provided. As we both appreciate, large-
entanglement obstructions typically are associated with the adverse scaling
where
is some (finite) single-qudit single-operation error probability, and the proposed remediations of this adverse scaling typically are equivalent to some variant of quantum error correction … even in experiments whose intrinsic dynamics seemingly is non-computational.
If there is any way to evade this generic mechanism, then I am eager to grasp it!
I guess one thing I should add is that our counterexamples construct states with high entanglement (according to Gil’s measure) *without* getting into the challenging parts of scalable FTQC. So our point is not a very deep statement, it’s simply that conjecture C is unrelated to the question of whether FTQC can work.
As for your point about epsilon vs n, note that for photons, \epsilon goes like e^{-\hbar\omega / k_B T}, which is one sense constant, but in another sense, exponentially small, and in practice can really be very small.
One more thing along these lines. John S. points out that the tensor rank is low for the W state, meaning that they are relatively uninteresting from the perspective of quantum computing.
Based on this, you could view our counter-example as saying that Gil’s entanglement measure counts too many things as entangled, including things that are so lightly entangled as to not provide computational advantage. Thus, it does not provide the quantitative Sure/Shor separator that he is looking for.
Let me explain the analogy a bit further.
Heisenberg’s uncertainty principle is due to the fact that, in order to locate a particle, you must shed light on it. Unfortunately, light is made of photons and photons are also particles. Similarly, in order to settle that a program is correct you have to write a proof. Unfortunately, proofs are also programs and this results in the following fact:
“The more you know about the correctness of a program, the less you become able to know about its complexity class, and vice versa.”
This is, IMHO, the reason why all efficient “solutions” to SAT are not known to solve every instance. They only have an acceptable probability of correctness – they’re called heuristic algorithms. Conversely, the algorithms used in artificial intelligence are often proven mathematically correct… but very little is ever said about their efficiency.
I wouldn’t insist, but my preceding comment is a step towards P=NP being undecidable. 🙂
In that regard, NP-completeness could be viewed as computer science’s counterpart of the quantum level.
… and the analogy goes further, as the macroscopic level is made of the quantum level just like NP problems are polynomially reducible to NP-complete problems.
I really think that defining suitable distances or topologies on the sets of problems, of proofs and of programs would suffice to prove that P=NP can’t be proved.
Aram and Steve’s state W and related states
The parameter K[ρ]. Here is a reminder what K(ρ) is. Given a subset B of m qubits, consider the convex hull F[B] of all states that, for some k, factor into a tensor product of a state on some k of the qubits and a state on the other m-k qubits. When we strart with a state ψ on B we consider D(ψ,F[B]) the trace distance between ψ and F[B]. When we have a state ρ on n qubits we define K(ρ) as the sum over all subsets B of qubits, of D(ρ[B], F[B]). Here ρ[B] is the restriction of ρ to the Hilbert space describing the qubits in B.
The states W. Next let me remind what are the states we talk about. We consider the state
. Let us also consider the more general state 
which is the transposition of all vectors 
where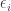 
are 0 or 1 and precisely k of them are 1. (So 
.)
Dycke state. In my paper I considered the state
as a potential counterexample to Conjecture C. Again let me remind you that conjecture C asserts that for a realistic quantum states ρ, K(ρ) attains a small value (polynomial in n). I thought about 
as a simulation of 2n bosons each having a ground state 
and an excited state 
, such that each state has occupation number precisely n.
While
is exponentially large in n a rather similar pure state , the tensor product of n copies of 
, is not entangled and for it K is n. So it is quite important to understand well what is the state which is experimentally created.
What conjecture 1 says: Already Conjecture 1 is relevant to Aram and Steve’s
(and the more general 
). The conjecture predicts that the noisy 
states are mixture of different 
, where k is concentrated around 1. It can be, say, the mixture, denoted by ![W_n[t]](https://s0.wp.com/latex.php?latex=W_n%5Bt%5D&bg=ffffff&fg=333333&s=0&c=20201002)
of 
with probability 1-t and 
with probability t. (Perhaps, with addition ordinary independent noise on top).
So we can ask two questions:
1) Is the noisy $W_n$ states created in the laboratory in agreement with Conjecture 1? If we realize
by k photons the question is if the number of the photons itself is stable.
Joe, when you refer to the state
that was constructed with reasonable fidelities, in the paper you have cited, what are the mixed state which are actually been created?
2) The second question is about a mathematical computation that extends what Aram and Steve did: What is the value of![K(W_n[t])](https://s0.wp.com/latex.php?latex=K%28W_n%5Bt%5D%29&bg=ffffff&fg=333333&s=0&c=20201002)
? Namely, if we have a noisy 
of the type I described above what will be its value of K? is it still exponential in n?
Leggett’s disconnectivity parameter. If somebody is willing to write down what is Leggett’s definition of his disconnectivity parameter and explain it this will make it easier to discuss Leggett’s parameter. The definition is short but I don’t understand it that well.
Hi Gil,
The paper I refered to was a survey paper, not any one experiment.
However, in quantum memory type experiments they aren’t actually explicitly trying to generate w-states. Their ultimate goal is to basically absorb a photon for some period of time and then emit it. The physics of the situation is such that the state of the vapour is pretty close to a w-state, but that isn’t really what they care about (although it is maybe what we care about), it is simply the mechanism for their trick to work. The fidelity I was talking about was of the emited photon. This is only indirect evidence of the w-state, and measuring the state of the vapor itself seems likely to be beyond our current technological capabilities, but I believe it is reasonable evidence that we can create w-like states on a large scale.
Hi Aram Joe all, The motivation behind the parameter K(ρ) was indeed coming from error correcting codes that correct c errors. There, small subsets of qubits behave like product states but for larger sets (of size c+1 if I remember right ) you will get substantial contribution to the terms defining K. As Aram and Stave showed much more mundane states like
have expoenential value for the parameter K.
I certainly agree that W does not look as expressing exotically strong entanglement. And I tend to agree that W-like states can be created. What we can think about is if such expected W-like states like those I described above also have an exponential value for K.
Also I am not sure if we exausted listing all possible ways that the state W can be implemented.
Hi Gil,
I was just trying to answer your question “is the W state realistic?”. I think we have pretty strong evidence that it is even at extremely large scales. Certainly we have not considered even a small fraction of the ways it can arise with relative ease, but I would have thought even the few examples considered thus far should be convincing enough on their own.
Right, Joe, thanks. I am quite convinced about W being realistic. My follow up question was how realistic W-like states look like. In particular, how do they look as mixed state approximations of W (This may differ for different examples which is why I thought it will be useful to consider more examples.)
This follow-up question is relevant to first being sure about the parameter K and also to Conjecture 1 which predicts how mixed state approximations of W look like.
I think that what makes the photon-based W states realistic is that the per-qubit noise decreases exponentially with photon frequency, or more precisely, photon frequency divided by temperature. (And this noise should be on the order of 1 / #qubits.) So large, nearly-pure, W states should be feasible. If I’ve calculated right, then this ratio should be on the order of 100, when the photons are visible light, and the temperature is room temperature. This means that thermal noise per qubit would be e^{-100}. I guess this means that other sources of noise will be more relevant. Although photon loss isn’t much of a risk. I’m not sure what the dominant source of noise would be, really.
Aram: Once you bring detectors into the picture, you would need to worry about dark counts, which would become more and more important as the probability of there being a real photon in that mode decreases. This doesn’t alter the underlying state, but would decrease the fidelity of any reconstructed density matrix.
Sure, but for the purpose of the conjecture, we don’t need detectors; we just need to believe that at some point, the state existed.
Leggett´s Dis-connectivity parameter (off line). begins when we are trying to create some programing strings on a programatic lang like de C plus , or C plus plus. it does not define the postions on a Matrix. we are considering that the zeros an ones are traveling at the speed of light. Eisenberg’s uncertainty says that in order to read a bit you have to write it first. there is nothing faster than the speed of light traveling in the empty space, once you go off boundaries of the domain of the Matrix P=1 the recording bits are unreachable. according to Bayes any statistical notacion or bit recorded on spaces (sideral) out of the reach of a logic gate disrupts the real time connectivity, lets say that you send an spatial probe out of the system and you need to comunicate in real time with it, you send the information of the programatic strings wherever they are, but the distance the probe is moving is a couple o billion light yeas away simply the information wouldn’t be there on time and several years later you receive some static final. what does it happen? you loose a grip of real time. Here Eistein talks about the light bending coefficient when the radius of the matrix integration domain goes off the limits of connectivity of communication of a logic gate. The generated inertial force at the end of the string will catch a gravitational force as the spin on the radius goes on. this is going to create an inverse value that is considered as antimatter modifying its structure . Einstein Observes the star lights of the super nova’s detonation(gamma rays) and sees that the exploding stars generate a light pulse that travels faster than the Limit of the light constant measured in an empty space. at this condition Eistein calls it Quanta. and states that Star Light travels in Quanta. so he does not takes C plus plus. as a solution for the dis-connectivity problem he divides P=1 between the sideral time and real time, obtaining B as a radical of the space-time P=1 equals P=-1 or inverse logic gate. as a radical of 1 he obtains K=0 because the bit traves in linear regression. this considerations came with the relativity theory where the speed of the light is relative to the conductor where it does travel. and to reconnect the logic gates in time space( two computers in sideral distances) needs to accelerate to C square times. through a gravitational compression that can liberate a propulsion force that breaks the speed of the Light. (Quanta is considered a worm hole), to create stacks for programing strings According to Bayes theorem requires to consider the variance and the deviation standard. here de Hue or deepness are a primordial problem due to the current flow in a quantum solid state receptor. the compression state for the Large hadron Collider that canot reach speeds faster than the Light. Tera-Electron-Volt cannot generate this antimatter needed for this kind of propulsion.
Please let me say that I too regard
-states as being realistic (that is, experimentally feasible). For me, the salient feature of 
-states is not their exponential-in-
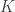-value, but rather their polynomial-in-
tensor rank.
Respecting tensor rank as a natural measure of quantum state feasibility, two recent survey articles (that IMHO are very interesting and well-written) are Cirac, Verstraete, and Murg “Matrix Product States, Projected Entangled Pair States, and variational renormalization group methods for quantum spin systems” (arXiv:0907.2796v1) and also Cirac and Verstraete “Renormalization and tensor product states in spin chains and lattices” (arXiv:0910.1130v1).
In the former we read:
and in the latter we read:
These considerations from Cirac, Verstraete, and Murg suggest that perhaps Gil Kalai’s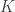
-measure might usefully be evolved into a rank-sensitive 
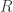-measure … the granular details of this modification are what I am presently thinking about.
Please let me thank everyone for helping to sustain this wonderful dialog! 🙂
As an addendum, it turns out that the above-referenced Cirac / Verstraete / Murg preprint arXiv:0907.2796v1 is substantially the same work as referenced as [3] of the Flammia/Harrow note “Counterexamples to Kalai’s Conjecture C” (arXiv:1204.3404v1). It is striking that one-and-the-same article serves simultaneously to: (1) inspire counterexamples to Gil Kalai’s specific conjectures, and (2) inspire confidence too that the overall thrust of these conjectures is plausibly correct. As usual, Feynman provides an aphorism that is à propos:
In the present instance, this would correspond to “We (believe that we?) know that Gil’s thesis is correct (but in what form?) however we have not (as yet?) proved it.”
Further respecting tensor rank, I tracked down the provenance of the Feynman quote (or misquote, as it turns out). From Feynman’s Nobel Lecture “The Development of the Space-Time View of Quantum Electrodynamics”:
With regard to product states, we have works like J. M. Landsberg’s “Geometry and the complexity of matrix multiplication” (Bull. AMS, 2008) to remind us of how very much is known about these state-manifolds, and equally strikingly, how very much is not known. And so it seems (to me) that Gil’s conjectures are very much in accord with this honorable tradition of mathematics and physics, of seeking to state concretely and prove rigorously, an understanding for which there exists an impressive-but-imperfect body of evidence.
Quantum FT separators, the parameter K(ρ) and the state W.
1) Conjecture C is meant to draw a line (of asymptotic nature) between states whose construction does not require quantum fault tolerance and states which require quantum fault tolerance. We will call such a proposed separation a quantum FT-seperator.
2) The border line was supposed to leave out quantum error correction codes that correct a number of errors that grows to infinity with the number of qubits.
3) The parameter K(ρ) was based on this idea since for an error correction code correcting c errors on n qubits its value is roughly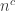
. However, as Aram and Steve showed a much more mundane state W has exponentially large value of K. This means that K does not capture what it was supposed to capture.
4) As mundane W is, it is interesting to examine how can it be implemented and what are the mixed state approximations that we can expect for W. (This is relevant also for my Conjecture 1.) In order to be sure that K is not appropriate to draw any reasonable line of the intended sort it will be useful to compute K for such W-like states, e.g. what I called![W_n[t]](https://s0.wp.com/latex.php?latex=W_n%5Bt%5D&bg=ffffff&fg=333333&s=0&c=20201002)
.
Aram and Steve’s qudit example and Leggett’s disconnectivity parameter
5) Aram and Steve’s qudit construction is based on the idea that for a state which can be created without quantum fault tolerance the parameter K(ρ) (extended to qudits) should remain low in every way we group qubits together into bounded size blocks. They exhibit a state which certainly can be prepared on 3n qubits so that when the qubits are grouped into sets of 3, the parameter K(ρ) for the qudits becomes exponential.
6) It is certainly a nice property for a parameter proposed as a quantum FT separator to remain low under such grouping. I am not sure that it is conceptually correct to make this a requirement and I will discuss this matter in a separate comment.
7) It is noted in this remark that a different qudit example in a similar spirit to Aram and Steve’s example may be used to exhibit a very mundane state with high value of Leggett’s disconnectivity parameter (in the way Aram described this parameter in this comment). Let’s discuss it!
Bounded depth circuit as FT separators
8) The principal proposed FT separator described in the post is based on bounded depth computation. With the exception of a comment by Aram, we did not discuss this proposal so far. One counter argument raised by Aram is based on nature’s ability to create heavy atoms. This is a terrific idea. It can be interesting to discuss if the process leading to heavy atoms requires some sort of quantum FT, requires “long” (high-depth) evolutions, or perhaps even exhibits superior computational power. (I am skeptical regarding these possibilities.)
9) It will be interesting to describe experimental processes that may exhibit or require long quantum evolutions.
10) One of the nice things about bounded depth classic computation is that it leads to functions with very restricted properties. Bounded total influence (Hastad-Boppana); exponentially decaying Fourier coefficients (Linial-Mansour-Nisan) etc. Are there analogous results in the quantum case?
11) The bounded depth parameter satisfies the grouping requirement because we can regard qubits operations as qudit operations and replace each computer cycle on the qubit levels by several qudit cycles.
Gil, thank you for this very fine summary. For me, the most natural candidate for an FT separator is the tensor rank, that is, “
-qubit states require FT iff their rank is exponential-in-
.”
Perhaps the main objection to this separation is not that it is implausible, but rather that (with our present mathematical toolkit) it is so very difficult to prove rigorous theorems relating to tensor rank. Christopher Hillar and Lek-Heng Lim’s preprint “Most tensor problems are NP-hard” (arXiv:0911.1393v3 [cs.CC]) provides an engaging discussion of these issue, with the witty conclusion:
From this perspective, perhaps progress in establishing (rigorous) Sure/Shor separations is destined to parallel progress in establishing (rigorous) complexity class separations.
To put it another way, we would be similarly astounded at any of the following four announcements:
• a rigorous resolution of
latex n$ quantum computation, or
• experimental evidence that Nature’s state-manifold is non-Hilbert.
And the mathematical reasons for our amazement would be similar in all four cases.
Hmmm … the concluding four-item list was truncated by a LaTeX error. The intended list was:
To put it another way, we would be similarly astounded at any of the following four announcements:
• a rigorous resolution of
, or
• a rigorous rank-based FT separation, or
• experimental demonstration of a large-
quantum computer, or
• experimental evidence that Nature’s state-manifold is non-Hilbert.
And the mathematical reasons for our amazement would be similar in all four cases.
Dear John, Lets me just first make sure that we all understand the term tensor-rank in the same way. It is the minimum number of product pure states required to represent your pure state as a linear combination. (Am I right?) Since we talk abbout approximation we perhaps better replace “represent” by “approximate”.
Anyway, tensor rank seems a natural thing to think about. (And I dont remember if I did not or just forgot.) I would worry that Aram and Steve’s qudit example may have large tensor rank in the qudits tensor structure.
I prefer talking about FT-separators and not about Sure/Shor separator mainly to avoid computational complexity issues.
The issue of Sure/Shor and FT separators is much simpler and clearer if we talk about noisy states and not about pure states. The simplest FT separator is a (protected) essentially noiseless qubit. It is an interesting problem (first to put on formal grounds and then to solve) if a single protected (essentially) noiseless qubit is a Sure/Shor separator.
Yes, let’s affirm that “tensor rank” shall accord with wikipedia’s definition of tensor rank (which is the same as your post’s definition) and that “approximate” is a more precise description of what we want than “represent”.
Hmmm … some subtleties associated to tensor rank, that are not mentioned in the Wikipedia article — in particular the distinction between the rank and the border rank of a tensor — are discussed in J. M. Landsberg’s “Geometry and the complexity of matrix multiplication” (Bull AMS, 2008). AFAICT the rank/border-rank distinction is not materially significant to rank-based FT separations. But who knows? I have myself encountered numerical instabilities that are associated to this distinction.
The main point is that Landsberg’s definition of tensor rank, given as Definition 2.01 in his article, provides a rigorous entré into a mathematical literature that is vast, broad, and deep. To thoroughly grasp FT separations, it seems plausible (to me) that we will have to swim in Landsberg’s mathematical ocean … or at least wade in it. 🙂
Tensor is the term used as “dynamic energy tension” inside the electron structure. there are two considerations about it, one is the electromagnetic field that considers the electron spin due to its structure, its divided in cycles, sine and cosine and its divided into bits and Bytes.4, 8, 16, 32,64,etc. logaritm progression, and the variant and covariant tensors that do not poses an electromagnetic field, but a gravitational tension. this inertial force creates a linear regression on the atom, not necessarily on the electron, this tensor can be found on the small particles as the Gluon, muon, etc. The term Quantic does not exist before Einstein comes out with the relativity theory of time and space, and writes a chapter making evident this difference between electromagnetism and gravity. The Q-bit o Quantum bit is the subatomic charge that can be recorded in a tight space as Hilbert`s calculations, however since the gravitacional compression came to the electronics field we can store more information in the same space, one picture just to fit in a 2 mega bites chip, now the same chip can be used for 2, 4, 8 giga bites, and so on. this compression rate allows to store more information, but to use the term Quantum bit, is needed to obtain the radical compression of 1=C constant of the speed of light so the exponential should be a quadratic equation. in this case we would be recording with radicals smaller than than the nano. P=1 as a matrix value has to be a cubic exponential. This Quantum bit o q.bit would be an antiquark or antiproton inside the programatic stack, the hertz wave runs at 2.4 giga hertz but this speed would not be fast enough to bridge a logic gate for distances where C the constant of the speed of the light is squared. we will get the Femto, Yocto atomic weight. usually this is the nuclear radiation value, this anti-q.bit its aut of the boundaries real numbers( Manifolds dilemma). the quantum bit is in what is called linear regression on time and space. The polinomial equations on integrals X,Y,Z. on a Matrix P=1 square. C=square create Linear regression strings on programming quantum bits that are defined By Plank, Einstein, with the term” Momenta” and Niels Bohr has to admit one antiproton in his atomic model. The standard deviation and variance creates the indexes that are considered “Jakobs Ladder equations” deviations on time and space.
Another parameter which can be relevant for distinguishing “simple” and “complicated” quantum states is based on the expansion to multi-Pauli operators. Suppose that your quntum computer is supposed to perform the unitary operatior U, and let
be the multi-Pauli expansion of U , namely the expansion in terms of tensor products of Pauli operators. Here S is a word of length n in the 4-letter alphabet I, X, Y, Z, and
is a complex number. For a word S we denote by |S| the number of consonants in S. Define the Pauli influence of U by:
We can consider I(U) as a complexity parameter. The advantage of using Pauli expansion is that it is much simpler compared to parameters like my K, and tensor-rank. (In some other cases it turned out that multi-Pauli expansion is the best way to express mathematically my conjectures.)
Gil, supposing that for an
-spin system, a family of unitary transforms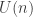 
is given such that 
is 
for some polynomial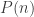 
. Then does it follow too that 
also is 
for some (different) polynomial 
? Here the physical motivation is that 
is a Hamiltonian that generates 
.
Dear John, I dont know the answer.
Such complexity
for “true quantum” gate 
would be less than for “pseudo-classical (swap)” gate 
. Is it O’K?
considered as consonant?
PS. Naive technical remark, is
Dear Alexander, Yes Yes Y is a consonant
PS2: May be in expression for
should be used 
?
Right, definitely! this is what I meant.
Pauli’s structure of analysis thrives on the electrons in the atomic level. The expansion factor of the atom when is stable and when is in expansion(explosion). Alfred Nobel obtains its fortune discovering the dinamite, the expansion factor when the atoms are at rest and in movement.here Pauli’s exclusion principle of the subatomic structure becomes a quantum step towards the principle of energy tensor. however the exponential reaction during its combustion (released energy) generates a wave length proportional to its compression state(solid quantum state). James clerk Maxwell separates the electricity from magnetism, what’s the deal, the electromagnetic field around an iron pigtal intensifies its force (K is the magnetic constant) this kind of compression does not have a quantum space (defined as an empty space in motion according to the relativity theory), the electron has a curly tensor as defined by Richard Feyman in Caltech in his book “The beat of a different hart “, during its expansion state releases a spin force(rip a curl), Einstein’s conjectures (Opinions) conduced him to split the atom and avoid the Fermion problem, because the tensor structure of the energy traveling in an empty space in motion had to carry a linear energy release effect and avoid the heating of the atom before it does releases the total amount of its energy,at the same time avoid the boundaries problems (manifolds) the total release of the energy in a chain reaction (obstructions on the combustion).over heating like in a nuclear reactor. The expansion factor is proportional at the inverse tensor (covariant), when this tension is on K=0 the inertial force forces the atom to travel backwards on time( this energy moving in an empty space in motion) creates a nonmagnetic tensor like antimatter. means that the nitroglycerin is condensed expansive fuel, as actinides, when they are in the presence of a detonator its energy release has a wave propulsion similar to the communications gate in your celular, reaches speeds almost like the speed of light, this is what is called a quantum bit o Q-bit. Pauli subatomic structure does not have quantic form. the nuclear energy release in a chain reaction inserts itself in the nucleus of the other atoms reproducing the same effect as splitting the atom due to the reason that is traveling faster than the speed of light (this is when is considered a quantic operator), Quantum computers use the same principle in the Hubble sideral observations, the Microchip that measures its operations in Gigahertz (speed), the Q-bits on memory stacks are compressed in giga bites, the programming string codes only create an assigned value of an operator, but if those operators are not defined on the memories arrays you can have a dis-functional programatic response. Quantum Physics are being used to simplifie multiple and complex operations.
Analogies
Learning from analogies is a difficult matter, and often discussing analogies is not productive as it moves the discussion away from the main conceptual and technical issues. But it can also be interesting, and being as far as we are in this debate, while concentrating on the rather technical matters around Conjecture C, we can mention a few analogies. (Studying analogies was item 21 on my list of issues that were raised in our discussion.)
1) Digital computers
Scott Aaronson: When people ask me why we don’t yet have quantum computers, my first response is to imagine someone asking Charles Babbage in the 1820s: “so, when are we going to get these scalable classical computers? by 1830? or maybe 1840?” In that case, we know that it took more than a century for the technology to catch up with the theory (and in particular, for the transistor to be invented).
The main analogy of quantum computers is with digital computers, and of the quantum computer endeavor is with the digital computer endeavor. This is, of course, an excellent analogy. It may lead to some hidden assumptions that we need to work out.
2) Perpetual motion machines
The earliest mention of this analogy (known to me) is in 2001 by Peter Shor (here):
Nobody has yet found a fundamental physical principle that proves quantum computers can’t work (as the second law of thermodynamics proves that perpetual motion machines can’t work), and it’s not because smart people haven’t been looking for one.
I was surprised that this provocative analogy is of some real relevance to some arguments raised in the debate. See e.g. this comment, and this one.
3) Heavier-than-air flight
Chris Moore: “Syntactically, your conjecture seem to be a bit like this: ‘We know that the laws of hydrodynamics could, in principle, allow for heavier-than-air flight. However, turbulence is very complicated, unpredictable, and hard to control. Since heavier-than-air flight is highly implausible, we conjecture that in any realistic system, correlated turbulence conspires to reduce the lift of an airplane so that it cannot fly for long distances.’ Forgive me for poking fun, but doesn’t that conjecture have a similar flavor? “
This is also an interesting analogy. The obvious thing to be said is that perpetual motion machines and heavier-than-air flights represent scientific debates of the past that were already settled.
4) Mission to Mars
Scott: Believing quantum mechanics but not accepting the possibility of QC is somewhat like believing Newtonian physics but not accepting the possibility of humans traveling to Mars.
5) Permanents/determinants 2-SAT; XOR-SAT
Aram: If you want to prove that 3-SAT requires exponential time, then you need an argument that somehow doesn’t apply to 2-SAT or XOR-SAT. If you want to prove that the permanent requires super-polynomial circuits, you need an argument that doesn’t apply to the determinant. And if you want to disprove fault-tolerant quantum computing, you need an argument that doesn’t also refute fault-tolerant classical computing.
This is a very nice analogy which gives a very good motivation and introduction to Aram’s first point. I also related to it in this comment. Of course, unlike the P=NP problem, or the question about solving equations with radicals, feasibility of universal QC is not a problem which can be decided by a mathematical proof.
6) Solving equations with radicals
When it come to the content, I do not see much similarity between QC and solving polynomial equations. But there are two interesting points that this analogy does raise:
1) Can we work in parallel? Is it possible to divide (even unevenly) the effort and attention between two conflicting possibilities? It is quite possible that the answer is “no,” because of a strong chilling effect of uncertainty. (See e.g. this comment.)
2) The failure for the centuries-long human endeavor of finding a formula for solving general degree-5 equations with radicals is not just “a flaw.” It was not the case that the reason for this impossibility was a simple matter that mathematicians overlooked. The impossibility is implied by deep reasons and represents a direction that was not pursued. It required the development of a new theory over years with considerable effort.
7) The unit-cost model
Leonid Levin (here): This development [RSA and other applications of one-way functions] was all the more remarkable as the very existence of one-way (i.e., easy to compute, infeasible to invert) functions remains unproven and subject to repeated assaults. The first came from Shamir himself, one of the inventors of the RSA system. He proved in [Inf.Process.Lett. 8(1) 1979] that factoring (on infeasibility of which RSA depends) can be done in polynomial number of arithmetic operations. This result uses a so-called “unit-cost model,” which charges one unit for each arithmetic operation, however long the operands. Squaring a number doubles its length, repeated squaring brings it quickly to cosmological sizes. Embedding a huge array of ordinary numbers into such a long one allows one arithmetic step to do much work, e.g., to check exponentially many factor candidates. The closed-minded cryptographers, however, were not convinced and this result brought a dismissal of the unit-cost model, not RSA.
This is an interesting analogy.
8) Analog computers
This is analogy that is often made. See, for example, these lecture notes by Boris Tsirelson, where Boris’s conclusion was that the analogy between quantum computers and both digital and analog computers are inadequate and quantum computers should be regarded as a new unchartered territory. I find what Boris wrote convincing. (I never understood though what is wrong with analog computers.) In Boris’s own words:
9) Magic noise-cancelling earphones
Here is an analogy of my own: We witness in the market various noise cancelling devices that reduces the noise up to 99% or so. Is it possible in principle to create computer-based noise cancelling earphones that will cancel essentially 100% of the noise? More precisely, the earphones will reduce the average noise level over a period of time T to O(1/n) times the original amount, where n is the number of computer cycles in T.
Another analogy is that we are struggling with a mismatch between “technology push” and “requirements pull”. At present the “requirements pull” is relatively weak — there isn’t much market-place demand for fast factoring engines, and as for quantum dynamical simulations, during the past 20 years the Moore-exponent of improvements in classical simulation capability has substantially outstripped the Moore-exponent of improvements in quantum simulation capability … and there is no obvious end it sight.
As for the proof technology push, here too we have only barely begun to integrate existing quantum algebraic-informatic tools with differential-dynamic tools. As Vladimir Arnold expressed it:
Conclusion: We stand in need of a version of Conjecture C that is designed so as to be simultaneously: (1) concretely responsive to the “requirements pull” of the 21st century, and (2) creatively amenable to an Arnold-style “technology push.”
Another very good analogy in my view is with Bose-Eisntein condensation. An idea that was theoretically proposed in 1924-25 and was first realized experimentally in 1995 after attempts to do so from the mid fifties. This is a great “role model” for the QC endeavor and it is also related to various technical issues related to our discussion. (Also some of the heroes of the BE story are now part of the QC efforts.)
Another interesting analogy with alchemy and the goal of transmuting gold into led was raised e.g. by Scott Aaronson in this discussion over Shtetl Optimized. What is interesting here is that the principle for why led cannot be turned into gold given by atomic theory and modern chemistry were of course of huge importance in science, and yet, one could say that now with subsequent further understanding one can argue that it is actually possible “in principle” (but we no longer care) to turn led into gold. (You can even say that understanding the principle for why it is impossible was crucial for understanding later on the principles for why it is possible.) See here for a related remark by Dick Lipton over my blog also referring to perpetual motion machine.
History repeats itself. Not even sure that these three problems – lead transmuting into gold, P=NP, large-scale quantum computing – are theoretically so distinct from each other…
I am looking at Conjecture C for codes
I cannot help but think about separability of pure states, and since we are talking qudits now, it is worth noting that it is possible to place upper and lower bounds on separable states around maximally mixed states.
http://arxiv.org/pdf/quant-ph/0001075v2.pdf
It is also worth reviewing
http://arxiv.org/pdf/quant-ph/9605038v2.pdf
If we think of noisy quantum systems as non-separable where system and environment are entangled, then the question seems to be whether we can identify some separable pure subsystem of the noisy system of some size with a measure c of the number of errors the subsystem can correct.
My thinking is that we really can’t answer this question without thinking dynamically, e.g. without thinking about the time dependence of the system. If we are thinking in terms of computing, we have to place a time envelope around the beginning and end time of the computation. So in this sense, one can think about there being a bubble in the mixed system that has sufficient life to complete some sort of operation.
This make one want to use constant c in the context of a measure of temporal pure states that follow a decay function like EXP(-ct) where the upper bound of c is limited largely by the remaining entropy growth in the larger noisy system.
Quantum teleportation gets around no cloning by destroying one copy and creating another with a spacetime gap between the two copies. So it doesn’t seem counterintuitive to suggest that we can introduce similar temporal restrictions on the code. So if we dump any notion of eternally pure states, and begin asking questions about the scalability of more temporal pure states, I think the size of the separable pure states will be largely dictated by the size of the larger noisy system and where that system is in its evolution with respect to some observer.
A piece of news related to the debate: Here at the Hebrew University of Jerusalem the new Quantum Information Science Center had its kick-off workshop, Yesterday, May 30, and I gave a lecture on the debate with Aram. Here are the slides of the lecture. It covered my initial post and Aram’s three posts but did not go into the rejoinders and the discussion. There were several interesting comments related to the discussion which I will try to share later.
As quantum information is an interdisciplinary area in the true sense of the word and also in the good sense of the word, an area that involves several cutting edge scientific topics, it is only natural that HU’s authorities enthusiastically endorsed the initiative to establish this new center. The entire workshop was very interesting, Dorit Aharonov gave a beautiful talk claiming that a new scientific paradigm of verification is needed to check quantum mechanics beyond BPP. This talk is quite relevant to a discussion we had here on the post: “Is this a quantum computer“. The other talks were also very interesting.
I’ve seen this dialog going from Polynomials to Black holes and seems to me that you are looking the “God”el’s particle.as refers in modern physics, the Dialog with “Aram” aic on the signature of the glyph-encrypted-black door.that talks about gods paradise is very similar to the quantum time-space on the “Tora” talks about creation “one empty space where he created the materials things”. Einstein said the same thing ” an empty space but he said (in motion)”.the Godels polynomial on the Quintic equation on a bi-dimensional where you take one ordinal line X to an exponential 5 “from one to five there is a gap to reach that place (here there is motion) ” this was not solved in that time. this gap created the Ana “frank”-incense room where it was an annex to the house where she was hiding. this gap factor is the same principle of the Quintic “mistere” of the Golden Shrine and the small temple behind it in Israel. This equation was discovered by the German Officers upon its denunciation. the separation of the origin of X to its radical, created a linear gap called hue, or deepness.So Einstein had to go on a Tri-dimensional ordinal sketch and Use the principle of “gravity as two forces that attract and repel each other” where the radical is a compression state (Quantum state). some get confused on this assumption saying gravity is = 2, where in reality is one in ground zero. so he decides to split the exponential function of one. and have 1/2 of the sine . 1/2 cosine =1. On the Quintic equation the observer sees the variable X moving from left to right or right to left. so he changes the position to Z variable. and he sees that the light bends upon the inertial force when is moving from X zero to X5 what you are seeing is that the point of origin moved because the place you are standing is moving also.(Galileo) paradox. so Einstein made some calculations and he discovered those two forces that counteract and he uses the equation on 8Times the radius or the speed of light, creating the “Octil” parameter. (Octli) so this inertial force would create the gravity needed to create a Quantum State of particles in Motion in an empty space.(Bose-Einstein Principle), this Gravity Shield (SchwarzChild ring of gravity equation), influenced by the spinning of the particles on a distant Polynomial would create a gravity line on X zero to X-1= radical.The first gravity force on “Z” when the integration of the variables on a displacement towards the point of 8Times the radius at the speed of light, has had surpassed the boundaries of the real numbers (manifolds).The numeric perception becomes not real and 1/2 can be considered different than the original values.(values of perception Jean Piaget). The quantum space is considered an extra dimension when the integration values(samples) are far more away of the distance of the speed of light.The uncertainty of finding the same spot in the same time space, in another dimension has brought the idea of Quantum Bits to make Tera Hertz fast microchips to make recording quantum-bits. however one bit second in the fire might seem like a year, or one billion year with Ruth might feel like a second.This are the principles of the Aramaic encryption lang.later on the Hittite Lang Shows some modification on time space, from the present to the future. Any space that you can see and perceive in your eyes has an arch function inside your mind. The phrase ” Victory is for Her whom wins with her sight and ankles” was used during the Roman Empire as a symbol of power. Who she is?. The Tevatron is trying to generate this gravitational force to accelerate the hydrogen in the fuel cell. and use water as fuel. The water as Fuel has to have this pressure, The fuel pressure sensor has to indicate the fission point where the hydrogen atom jumps from one dimension to another generating friction and temperature within himself.its called the Mikamoka antimatter bit. The Borgia Codex shows some codifications that talk about this empty space in motion but is similar to the old Babylonian cuneiform script of Mount Sinai. Shalom.
One interesting issue that was raised by Nir Davidson in our quantum information center kick-off workshop is the “paradox” regarding chaotic behavior in quantum and in classic systems. In a classic chaotic system two nearby initial states may be carried far apart by the dynamics. In fact, their location may become statistically independent (in a certain well defined sense). In “contrast” for two nearby states in a quantum evolution their distance (trace-distance) remains fixed along the evolution. Nir described a formulation by Asher Peres for the “paradox” as well as how to solve it, and some related experimental work.
This issue is relevant also to classical and quantum computers. If we corrupt a single bit in a digital computer then as the computation proceeds we can assume that this error will infect more and more bits so that the entire computer’s memory will be corrupted. In “contrast” if we let a quantum noise effect a single qubit and continue the quantum evolution without noise, then the trace distance between the intended state and the noisy state remains the same. What can explain this difference?
The answer (I think) is quite simple. It has to do with the distinction between measuring noise in terms of trace-distance and measuring it in terms of qubit-errors. When you corrupt one qubit and let the error propagate in a complicated noiseless quantum computation the trace distance between the intended and noisy states will be fixed but the number of qubit-errors will grow with the computation, so just like in the classical computer case the noise will effect the entire computer memory. This is related to the fact that the main harm in correlated errors is that the error-rate itself scales up.
Had computer science been a business of engineers and physicists right from its beginnings, I think that greater emphasis would have been put on processes rather than on programs. Processes are physical objects whereas programs are just mathematical ones – and processes are everywhere in Nature.
For example, the fact that it’s much more difficult to factor a large compound number than it is to multiply two large primes is somewhat reminiscent of the nuclear force that glues the protons together inside atoms. Breaking a nucleus apart requires a lot of energy as well.
When the unsolved problems of complexity theory are considered more systematically with a physicist’s eye, maybe new laws for the physics of computing will be discovered instead of new axioms and proofs about algorithms.
To put it differently: trying to guess the behavior of a process by means of its program is like trying to guess somebody’s life by means of their DNA code. Processes are executed by physical devices which are themselves subject to the laws of physics.
That doesn’t answer the PvsNP question – which I believe is undecidable. But it might explain why the world seems to behave as though P!=NP.
Hi Serge, regarding the P=NP problems and your beliefs about it. The possibility that the question is undecidable was raised and there is some related research agenda. Unfortunately, proving definite results in this direction appears to get “stucked” even a bit earlier than proving definite results about computational complexity hardness. (If you want to check your reasonings regarding P=NP being undecidable one standard things to do it to try to see the distinction with problems like 2-SAT that are known to be feasible.)
You mainly raise two other issues which seem interesting. The first is about our inability to predict the evolution of a computer program (described, say by the DNA code) when the evolution depends on unpredictable stochastic inputs. The second is about our inability to predict the evolution of a computer program (again a DNA code is an example) when we do not know precisely what the program is. (Also, the analogy between factoring and breaking a nucleus to parts is cute, but its is not clear how useful it can be.)
The distinction between (physics and engineering) processes and (mathematical) programs is not clear.
Hi Gil, thank you very much for your interesting answer.
A clear distinction between programs and processes is useful in operating systems, a process being a specific execution of a program. One program leads to infinitely many possible executions of it. When mathematicians speak of a program, I think they also mean all its potential executions.
Regarding PvsNP, there might exist a polynomial algorithm for SAT but executing it would go counter physical limits, such as a program too big to fit into memory for example. Or maybe our brains just couldn’t understand it and therefore nor even design it.
In addition to the unpredictability of the behavior of programs due to unpredictable stochastic inputs or to unknown code, in some cases that behavior could be undecidable itself. I’m thinking of the algorithm that Ken commented on in “The Traveling Salesman’s Power”, saying there’s an already-known algorithm A accepting TSP such that if P=NP then A runs in polynomial time.
John Preskill’s recent paper Quantum computing and the entanglement frontier touches on many issues raised in our debate. Very much recommended!
Gil, please let me commend too this same Preskill essay. In it we read the following passage thought-provoking passage (p. 5):
Adopting Preskill’s language to express the intuition that motivates Kalai Conjecture C (as I read it) leads us to the notion classical computers suffice to verifiably reproduce any-and-all simulations of quantum computers, insofar as those simulations apply to feasible physical experiments. And here the notion feasible physical experiment is to be taken to mean concretely, any-and-all physical system whose Hamiltonian / Lindbladian generators are stationary.
In the preceding, the stipulation stationary is chosen deliberately, with a view toward crafting a concrete presentation of Conjecture C that affords ample plausible scope for near-term advances in practical simulation, without definitively excluding a longer-term role for quantum computational simulation. As a colleague of mine from Brooklyn was fond of saying, such a conjecture would be “better than ‘purrfect’, it would be ‘poifect’!” 🙂
Dear John, I have similar sentiments regarding the role and scope of Conjecture C. The draft of my post had a long obituary of Conjecture C (in the form originally made), starting with:
“Conjecture C, while rooted in quantum computers skepticism, was a uniter and not a divider! It expressed our united aim to find a dividing line between the pre- and post- universal quantum computer eras.”
Following Ken’s mathematical-formulations-as-cars’-engines metaphor, the following picture of me and Conjecture C was proposed http://gilkalai.files.wordpress.com/2012/06/conjecturec.jpg
LOL … Gil, perhaps Conjecture C may yet be reborn as a phoenix arising from the ashes! 🙂
Indeed, we have good reasons to give up on the parameter K(ρ), but we did raise some appealing alternative parameters. In particular, the conjecture that the depth of quantum processes is essentially bounded is interesting both from the conceptual and technical points of view. (The idea that the emergence of iron is a counter-example is terrific, but I do not think that it is correct…)
As I am reading the the Preskill paper, my thoughts are wondering to questions of examples of brute force quantum computers. The idea is this, think of LHC. What is it actually doing? It is trying to identify particles predicted by various models of particle physics, and it is also verifying production cross sections of those particles. So in some sense, we have models that can make predictions that are in some way computable using a classical computer, and we are building a machine that can verify that those models are accurate. So what is the LHC? Is it a machine or a Brute Force Quantum Computer?
No one is questioning that by accelerating particles and smashing them together we are generating new particles that follow some sort of function, however neither is any one questioning that what the LHC is simulating is an earlier state of the universe (and that might be a good question to ask).
Another more accessible potential example is found in the study of fluid dynamics. Although we have fairly good classical formulas for modeling fluid flow in several situations, The modeling of complicated turbulent systems is extraordinarily difficult, and in many cases scale models must be produced in order to measure the “real” fluid flow of the system. Again, if we accept a quantum existence, what have we actually built with our model? We have resorted to a type of brute force method in order to solve a real world computational problem.
As I think further about the question of QECC, I can’t help but think of the similarity between the difficulty of developing QECC and the difficulty in building stable fusion reactors. In a fusion reactor the goal is to build a stable, long lasting state of matter, invariably we can see that state as a quantum state, and the problem is similar. How do we keep the state stable so that “noise” from the environment doesn’t collapse the state? Once again, we are looking for a brute force method to solving an otherwise computational problem.
Freeman Dyson recently published a book review where he compared string cosmologists to natural philosophers and other “creative” thinkers. However, what he failed to recognize is that questions being asked in those explorations do have intersections to real questions in quantum computing, such as the relationship between axions and anyons, as highlighted by Wilczek [2].
This brings me some of the more current question regarding the debate surrounding SUSY and theory that rely upon its existence. I look at the recent Straub paper [3] and see a graph with the SM as a point in vastly larger parameter space. Although by design, all the other potential models contain the SM as a shared common point, I can’t help by think about the situation coming from the other direction an looking at all the potential models that have the SM as a common point.
Although I am not a subscriber to any notion of a multiverse as envisioned by sci-fi and pop sci writers, I am interested in this idea of other stable solutions, or perturbtions of our particular stable solution.
Preskill does and excellent job of highlighting the question of what can’t be simulated on a quantum computer. We can’t give mass to a simulation in a quantum computer, however we know that there are several solutions out there that could be explored that do not require mass, and I think those are something worth exploring.
[1] http://www.nybooks.com/articles/archives/2012/apr/05/science-rampage-natural-philosophy/
[2] http://blogs.nature.com/journalclub/2009/03/frank_wilczek_1.html#/fn10
[3] http://arxiv.org/abs/1205.6094
The universe: is it noisy? Is it a quantum computer? why not two non-interacting quantum computers?
The idea of the entire universe as a huge quantum computer was mentioned in several comments (and is an item on our long agenda). Also, the universe being described by a pure quantum evolution was mentioned and was related to Aram’s second thought experiment. It feels rather uncomfortable to talk about the entire universe, or to draw conclusions from it, but let me try to make some comments.
1) The claim that the entire universe runs a pure evolution seems reasonable but not particularly useful. (There are theories suggesting otherwise which are outside of quantum mechanics.)
2) The claim that the entire universe is a huge (noiseless) quantum computer which computes its own evolution is also made quite often. Again, it is not clear how useful this point of view is. And I am not sufficiently familiar with the literature on this. The universe as a huge noiseless quantum computer can be regarded as an argument against the claim that quantum computers are inherently noisy.
3) As we noted already, quantum computers are based on local operations and therefore the states that can be reached by quantum computers are tiny part of all quantum states. For example, a state described by a generic unitary operators is unfeasible. (In our off-line discussions we raised the question if such non-local states appear in nature.)
4) An appealing possibility (in my view) for our universe is that of two (or several) non-interacting (or, more precisely, extremely weakly interacting) quantum computers. We can have on the same Hilbert space two different independent tensor product structures so that every state is a superposition of two states, each described by one of two quantum computers. In this case, states achievable by one quantum computer will be nearly orthogonal to states achieved by the other. (This possibility does not rely on the hypothesis of no quantum error-correction, although it will be “easier” for two quantum computers not to be able to interact when there is no quantum-error correction around.)
5) The idea of the universe as a quantum computer which runs quantum error-correction is used in the paper Black holes as mirrors: quantum information in random subsystems by Hayden and Preskill. For what I understand, in this paper, certain quantum states in a black hole are required to behave like generic unitary states, and since such states are infeasible, states with similar properties arising from quantum error-correction are proposed instead. It will be interesting to examine if Hayden-Preskill’s idea can work with quantum error-correction being replaced by a two non-interacting quantum computers solution.
Usually the chinese people writes “peoples” as plural when it is already “people” plural. the same mistake was done in Mao Tze Doung’s biography. we are acostumed to take somebody’s else mistakes as truthful.”Weylan” means labor camp woman. Mao’s mother, and Bolchevique’s holy Icon that represents the mother’s nation of the of the truthful patriots. Charles Marx was a German Jew that wrote “Das Kapital”, Einstein was a German-Jew also. both theories shocked the world with conjectures on Human quality recognition and equal distribution of the income. while the occidental countries constructed their kingdoms based on Slavery and human degradation arguing that they are doing good to humanity. Why two supercomputers can’t be enabled to work together?. their programers keep the security codes on the so called star wars. where the code couldn’t be cracked, hijacked, or erased. in order to deviate their commanding source and get rid of them in case of a confrontation. What is the problem with the quintic equation being solve by radicals? that we do not have an exact number on the square of 2 or 1. all the operators are built in hertzian operations. how fast an electric current travels through a conductor of logic gates flipping them on zeros or ones. the Quantum bit here has been recorded in a different wave lengt not in a different code source, this wave lengt is exclusive of the Pentagon or the Kremlin to operate their military satellites. its something like the chess board, it dos have to parts that are interacting with each other to find the ponderation of the code encrypted in each memory stack. however the quantum bit presents a conflict. where the antimatter is present as an antiquark in a wave lengt.Einstein’s equation E=MC square caused international Mockery and Histeria between the Mathematicians and Physicists, Why? the Godel’s inability to solve the quintic equation was solved upon a logic aberration. C= constant of the speed of light its the maximum speed of the light in an empty space, so how are you going to accelerate faster than the speed of light to get C square?. somehow the universe is noisy because they found sounds of exploding stars and this shock waves travel faster than the speed of light. its what is called Quanta something like ether, or antimatter (The Micamocka chocolate chip), its the same antimatter quantum bit that the Tevatron is looking for in the Large hadron Collider, and is obtained in a Higgs equation through a massive collision of particles where the expansion wave has to be similar to a super nova star, however they do not have the expected results. this event should create a time space distortion where two or more atoms are trying to occupy the same dimensional time space, this is called atomic fission and is found in radioactive materials that eat the surrounding material (Chernobyl).there is an angle deviation in the equations (Bishop) that acts as a counter weight in the atom spin when reaches C square. that factor is what is called gravitational spin. The negroe playing chess with the Rabie is symbolic of the arch of the alliance, but that does not make them geniuses like you say. Bobby Fisher, Karpov, Kasparov and many others work on an equilibrium equation where any step of a horse changes algorithmically all the equation. Mans visual field is 20-20 while the Horse is Greater 30-30 so this difference gives you a linear regression. Check once you are the king your place its the “Ara” aramaic. That becomes a black hole to the gravitational field when you are out of boundaries. Quantum bit (Antiquark) that is present before the integration of the mass hertzian wave. Eistein used 8Times the radius of the speed of a light emitter to create the gravity field where you can encrypt any antimatter code. Megabucks trick,National Lotto, and other crap games. The tower J is the Jocker’s Club, Who’s club is the Tower B?.
Heisenberg’s uncertainty is about How sure are you about hitting the nucleus of an atom in a chain reaction if you cannot comeback to the same place you left when you went up to a quintic polinomial, when it does involve exponentials on Csquare.The radicals are afected inversely.
Cat-state
I gave a talk at the HUJI CS theory seminar on matters related to my conjectures and the debate and there were several interesting comments by Dorit Aharonov, Michael Ben-Or, Nadav Katz , and Steve Wiesner.
Dorit suggested that experimental cat states with huge number of qubits are counterexamples for the conjecture on bounded depth computation.
This is a Good point!! I should certainly look at it.
One thing I never explained is why I considered Aram and Steve’s example as a counterexample to my conjecture C. The setting of conjecture C was to find limitations for states achieved by noisy quantum computers with realistic noise models. The prior assumption you need to make is that the noise on gate is of arbitrary nature. (And, in fact, for my full set of conjecture you need to assume that information leaks on gated qubits/qudits are positively correlated). Aram and Steve had two examples. The first is based on qudits. This is an interesting example, and certainly my conjecture C should extend to qudits. But in Aram and Steve’s example the noise on gates is not of general nature but rather of a very structural nature. So this does not apply to the right extension of Conjecture C to qudits, although it does impose an interesting condition on “censorship conjectures.”
The second qubit example is more convincing. (Ironically it is quite similar to an example I proposed myself in 2007.) A&F proposed a pure state which seems easy to approximate where my entropic parameter is exponential. What happens for mixed states which represent realistic approximation for this state? If the parameter is exponential for them this is a counterexample for my example. If it is not, it shows that the entropic parameter I defined is seriously flawed. (It will be interesting to know which possibility is correct, but in both cases I regarded my original entropy-based parameter as inappropriate.)
Looking again at Aram and Steve W-state proposed as a counterexample to my conjecture C from the perspective of what we know today about NISQ systems, I think we need to reconsider the question if this is indeed a counterexample and check the matter more carefully.
One way to go about it is to approximate as good as we can (or specifically for the purpose of maximizing K) the W-state using IBM or Google (or other) quantum computers and try to compute my parameter K as a function of the number of qubits n. The problem we might face is that the fidelity decrease exponentially with n and this may cause K to be bounded by a polynomial.
Since August 2021, Aram, Steve and I had an easy going discussion of Conjecture C, and recently I wrote up my critique of Aram and Steve counterexample in the paper “Conjecture C still stands”
https://arxiv.org/abs/2209.01648
As I write there, it looks that if you interpret the conjecture as applying to quantum computers then the emergent picture from experimental progress of the past decade on noisy intermediate scale quantum (NISQ) computers suggests that W-states, as simple as they appear, cannot be achieved experimentally by NISQ computers, and can not be constructed without quantum fault-tolerance.
The wider interpretation suggested by Aram and Steve is welcome, but the argument they provide that W-states (with exponential value of
) appears in nature is incomplete. (Indeed it is a fascinating problem if this is the case.) Their argument was perhaps sufficient to move our 2012 debate to other directions, but not enough, in my opinion, to justify the definite claims in their paper.
At present, the best candidate in my view for a “Sure/Shor seperator” is simply a “distance-5 surface code”.